核心素养导向下的单元整体教学策略

邵艺光

《义务教育数学课程标准（2022版）》（以下简称新课标）确定了核心素养导向的课程目标，课程目标的达成离不开数学课程内容的有效设计，体现结构化特征的课程内容有利于发展学生的核心素养。单元整体教学紧扣单元整体目标，遵循单元教学内容的内在逻辑关系，以核心概念统领，整体设计，分步实施，有助于帮助学生构建知识体系，促进学生核心素养的有效发展。本文以人教版小学数学为例，指向核心素养，提出相应的单元整体教学策略。

一、概念统整，从点状走向网状

有限的课时与不断增多的知识之间存在矛盾，而概念统整能够将单元内容结构最优化，使碎片化的知识进行有机联系，便于记忆和迁移。以学科大概念作为统整，推进单元整体教学，应聚焦学科本质，利用大概念揭示事实性知识背后的规律，连点成線，由线成网。

新课标对“空间观念”的内涵定义中提及，要能够“想象并表达物体的空间方位和相互之间的位置关系”。以《位置与方向（二）》一课为例，其学科大概念为“方向和位置”，即物体在空间中的位置可以被定量描述。

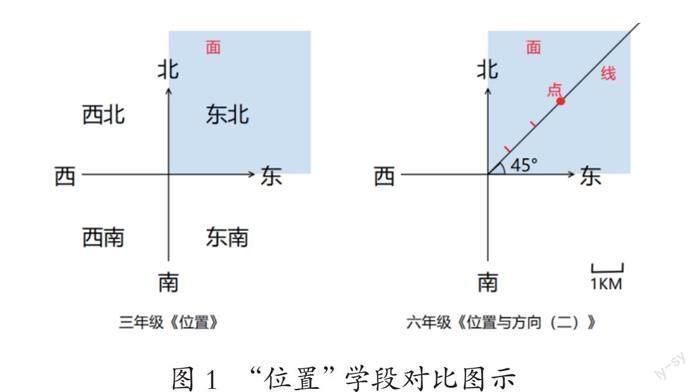
图1 “位置”学段对比图示

关于位置与方向的学习，学生从三年级下册的“东西南北”等8个方位过渡到六年级上册用“方向”和“距离”共同确定并描述某个点的位置（如图1所示）。以大概念统整后的教学需要对比思考，这两个学段的学习有什么不同？本质是什么？通过动画演示，学生能够感受到三年级对某点的描述更多停留在某个“面”上，是一个大致位置。到了六年级，因为有了更具体的方向，就从方位（面）过渡到方位角（线），又因为有了确切的距离，就能从方位角（线）过渡到精确的位置（点）。由此，从面到线再到点，对物体的描述就有了定量刻画。

教师还可以引导学生结合五年级的“数对”和六年级的“方向和距离”确定位置，继续思考不同和相同之处。第三学段学业要求提出，要能“通过图形位置的表达，理解坐标的意义”。实际上，前者是直角坐标的雏形，后者是极坐标的雏形，两者可以相互转化。小学阶段两者的表现形式不同，前者建立的是方形网格，采用的是“列”和“行”描述具体位置；后者建立的是同心圆网格，采用的是“方向”和“距离”来描述具体位置。虽然描述方式不同，但是都需要两个量才能定量描述一个点的位置。

新课标对图形的认识模块提出了具体内容和学业要求，应从图形元素、图形特征、图形关系入手，形成一个完整的图形网状结构。例如，四年级《平行与垂直》单元，其起始学科大概念为“两条线的位置关系”，主要研究“平行”“垂直”这两种关系，继而从这两个基本概念深入，探索平行四边形和梯形的图形特征，研究点与线的关系。

进行单元整合前，过去的教材主要分成两部分，先是线与线的关系，进而再研究图形之间的关系。而在大概念统整后，相当于对单元的学习进行主线梳理和提取。在单元内部，以线与线的位置关系作为学习主线，由平行概念出发，研究平行四边形和梯形，辨析两者之间的区别在于平行的对边有几组；由垂直概念出发，研究图形的高，明晰高的本质是点到直线的距离，从而拓展到所有几何图形的高都是一致的。

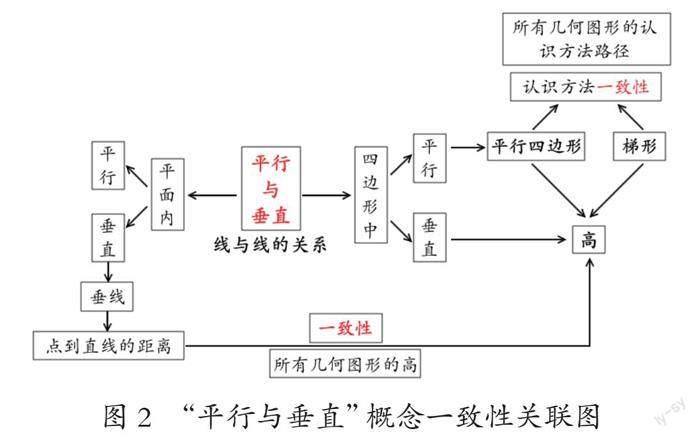
空间观念是指对空间物体或图形的形状、大小及位置关系的认识，在以此核心素养为导向的单元整体教学中，笔者尝试突出概念本质，从而构建以“平行”概念为主线的图形认识与图形关系，以及以“垂直”概念为主线的图形要素与图形特征。如图2所示。

图2 “平行与垂直”概念一致性关联图

借助大概念的统领，不论是跨学段还是跨年级单元，相同知识或相似知识都能在深入剖析中对比教学，聚焦本质、活化知识，发展学科核心素养。

二、知识关联，从零散走向结构

小学数学单元整体教学立足于小学数学知识的内在关联和学生实际的数学经验、能力素养和认知规律，以现行教材所划分的单元为基础，在整体把握教材内容和教学资源的基础上，将所要教学的某一主题内容有逻辑、有顺序地重新优化与组合，再以整体渐进的方式推进教学。笔者认为，知识关联是实现学生认知结构的基础，有助于将线性知识形成认知网络。

例如，学生在学习“比”之前，已经有了一定的生活经验，如“果汁中纯果汁和水的质量比是1∶4”“数学课本的长宽比是26∶18”。教师应基于此经验，融合学生已经学习过的关联知识，充分挖掘“比”的意义。对纯果汁和水的关系表达有所不同：二年级时学习的除法，学生借助“每份数”和“份数”的概念可以表达为“将纯果汁看作1份，水就有这样的4份”；三年级学习了“倍”，可以表达为“水的质量是纯果汁的4倍”；五年级学习了“分数”，可以表达为“纯果汁的质量是水质量的1/4”。六年级将要学习的“比”，无非是在学生已有的知识经验上再进一步串联“份数”“倍数”“分数”三者之间的关系，拓宽“比”的内涵与外延，在“倍”和“分数”中感受“比”，明晰此时的两数关系是“比倍”，而非“比差”。

在数的认识领域，打破自然单元的界限，打通不同学段的层级，学生在不断深入中探寻知识之间的关联性，用旧知识（份数、倍数与分数）唤醒新知识，用新知识（比的意义）活化旧知识，新旧知识关联处（两数关系）即知识生长点（比倍关系），亦是素养发展处。

知识的关联无处不在，除了在数的认识领域以外，图形与几何领域也尤为明显。例如，六年级《多边形的面积》总复习时，教师可以前置学习任务，让学生用合适的方式自主梳理学过的平面图形面积的计算过程。学生能够联想、提炼不同平面图形面积的计算推理过程，如长方形和正方形利用数方格的方法，数的是“有几个这样的面积单位”；平行四边形、三角形和梯形均利用转化的思想进行推理迁移；即使是曲面图形圆，也可以利用这样的方法学习，区别在于需要分成若干（偶数）等份，再拼成一个近似长方形进行推导。教师要做的是在此基础上更进一步启发学生思考整理后的体会，从而提炼平面图形面积计算的共同点：一是平面图形面积测量和计算的本质是“面积单位个数的累加”；二是平面图形面积推导和计算的通法是割补及转化；三是平面图形面积公式推导的关键点是转化前后“变与不变”的量。

小学数学单元整体教学要立足于学生知识经验的起点和关联点，才能更好地找准学生思维的难点和痛点，帮助学生整合零碎的知识点，从零散走向结构，在构建知识网络的过程中理清知识脉络，形成相应的思想和方法，发展多种核心素养。

三、方法一致，从特殊走向一般

新课标对第三学段“数与代数”的学业要求指出，数的运算教学应注重对整数、小数和分数四则运算的统筹，让学生进一步感悟运算的一致性。学生应理解整数、分数、小数的加减运算都要在相同计数单位下进行，感悟加减运算的一致性。

例如，在学习五年级的《同分母分数的加、减法》之前，学生已经有了三年级学习《分数的初步认识》的經验，通过前测笔者发现，对同分母分数加、减法的计算，大部分学生已经掌握，那么这节课重点要突破什么内容呢？

首先，通过自主探究，学生采用画图等方式探索3/8+4/8的计算过程，在说理等环节理解3/8+4/8的含义，即“3个1/8加上4个1/8是7个1/8”。其次，进行结构化整合，关联课前出示的整数加法3+4=7，小数加法0.3+0.4=0.7，启发学生思考三者的相同点和不同点。在讨论和辨析中，学生发现3+4=7就是3个一加上4个一等于7个一，0.3+0.4=0.7就是3个0.1加上4个0.1等于7个0.1，同样的道理，3/8+4/8表示3个1/8加上4个1/8等于7个1/8。看似不同的式子背后本质却是一样的。相同点在于，不论整数加法、小数加法还是同分母分数加法，这三道算式最终都可以简化为同一个算式，即3+4=7，在此过程中引导学生思考，理解背后的原理实际上也就是计数单位个数的计算。学生在深入思考后会发现，其实“数的运算”道理都一样，其本质就是“数一数有几个相同的计数单位，再相加”。由此迁移到减法的运算。甚至到了六年级的分数乘法与除法，也能用这样的方法迁移。

例如，2÷2/5=10/5÷2/5=（10×1/5）÷（2×1/5）=

10÷2=5，这个运算过程与小数除法1÷0.2=（10×0.1）÷

（2×0.1）=10÷2=5是一样的，都可以提炼为整数除法10÷2=5，用一个式子串联三种不同的数运算，让学生感悟即使在除法中也可以用加减法的通法进行迁移，本质依旧是计数单位个数的计算。

如此一来，在单元解构和重构中通过算理的深度挖掘，聚焦方法的一致性，通过算法验证算理，在辩证的深刻感悟中打通不同“数概念”运算方法的连接，使运算通法得到迁移，形成运算方法体系，发展学生的推理意识及运算能力。

通过案例分析和实际教学发现，学生对部分知识和方法可以进行自主迁移，但可能更多地停留在模糊的方法模仿上，不一定真正理解方法背后的原理，教师在进行单元整体教学时恰恰需要关注这些一致的原理和方法，帮助学生从“形”走向“理”，从特殊举例走向一般通法，真正体会数学的本质和单元整合的妙处。

四、结构延展，从平面走向立体

新课标指出，在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系。因此，教师要帮助学生学会用整体、联系、发展的眼光看问题，从而发展核心素养。

“圆”作为小学阶段最后一个平面图形，以自然单元为视角，是起始课，连接圆周长和圆面积、方与圆的关系。教师可以在学生掌握圆的各部分名称和特征后，启发学生思考接下来可能研究圆的什么内容，学生很容易将之前的学习经验融入本次的学习内容，形成研究图形的认知结构——从具象认识（表象、特征等）、图形属性（周长、面积等）以及与其他图形的关系三个方面展开研究。

以重整单元为视角，是总结课，联系正方形、正三角形等一系列平面图形。在教学中，教师可以通过总结提升知识的价值，建立起有意义的延展结构。如图3所示，教师追问：“正方形与圆存在什么关系？”在观察中学生会发现，圆内接正多边形，从圆心到正多边形的顶点距离相等，正多边形有几条边就有几个顶点，就有几条相等的线段。当边数n增大时，圆的内接正n边形的周长趋于圆的周长（外切正n边形亦如此），它们的面积也会趋于圆的面积。在此过程中，学生逐步感受到极限思想和我国古人“割圆术”的智慧。同时，能够反向验证圆作为“正无限多边形”有无数条相等的线段（半径），打破几何直观层面（折、量等）思维，进一步从几何推导层面验证墨子提出的“圆，一中同长也”，深入理解圆的特征与内涵。

以上维度都是基于学生对平面图形的深度理解，以单元为视角，将原有认知结构纳入新的认知结构中进一步延展。前者形成了平面图形研究内容的认知结构，后者形成了平面图形特征关系的认知结构，从静态教材内容走向动态认知结构，使思维更加立体化。

五、结语

总而言之，大概念的统领、知识之间的关联、方法一致性的探寻、认知结构的延展等单元整体教学策略有利于挖掘学科的本质、形成知识体系、促成方法迁移、完善认知结构，是实现课程内容结构化的重要抓手，有助于促进核心素养导向的课程目标落地。

注：本文系厦门市同安区教育科学“十四五”规划2022年度课题“基于深度学习的小学数学单元教学研究”（立项批准号：KYX2206）研究成果。