属性集变化下序决策信息系统的增量属性约简算法

张义宗 ,王磊* ,徐阳

（1.南昌工程学院信息工程学院，南昌，330099；2.江西省水信息协同感知与智能处理重点实验室，南昌，330099）

粗糙集理论是1982 年波兰数学家Pawlak［1］提出的一种能够有效处理带有不确定性、模糊性、不精确性数据的数学工具，由于其解决实际问题的有效性，被大量应用于机器学习［2-3］、模式识别［4］、数据挖掘［5］和知识发现［6］等领域.属性约简是粗糙集理论中的核心与热点研究问题之一，旨在找出与决策信息系统分类能力一致的属性子集，达到决策信息系统属性降维的目的.

经典粗糙集理论以等价关系对论域进行划分形成的等价类为研究基础，但其不适合处理属性值具有偏序关系的数据.为此，Greco et al［7-8］基于优势关系对经典粗糙集方法进行推广，提出优势粗糙集方法（Dominance Rough Set Approach，DRSA），而DRSA 近似集的运算对象是决策类的上（下）向联合集，由此给出了上（下）向联合集的上、下近似集的定义.此后，众多学者对优势粗糙集方法进行了一系列的研究和推广.李艳等［9］深入研究了不协调目标信息系统的属性约简，在优势关系上给出了浓缩布尔矩阵的概念来计算属性约简.Li et al［10］针对区间值序信息系统提出一种基于优势关系的特征选择（属性约简）方法.Du and Hu［11］针对一致不完备序信息系统的属性约简问题，基于可分辨矩阵和可分辨函数，提出一种计算所有属性约简的方法.Yang et al［12］将优势关系拓展到区间值决策系统上，提出基于α-优势的粗糙集模型，并给出了上、下近似的计算方法.Zhang and Yang［13］将α-优势推广至集值信息系统，结合合取和析取给出了两种新的优势关系，并基于此提出集值决策表的特征选择（属性约简）方法.以上研究均是对优势粗糙集模型的扩展和推广，可解决不同类型数据集的属性约简问题.

然而，实际生活中数据的属性集会发生动态变化，相应的属性约简结果也随之变化，使用非增量属性约简算法对属性集动态变化的数据进行属性约简是不可行的，因为这会重复计算未变动前的部分属性，增加计算成本，在大数据集上甚至无法满足其属性约简的效率要求.因而，众多学者针对属性集动态变化的序决策信息系统展开了一系列研究，如Luo et al［14］将知识粒度引入序集值决策信息系统，对系统中属性增加和删除的情况，基于矩阵提出一种增量更新近似集的方法.Wang et al［15］针对有序信息系统多维变化的动态更新近似集的问题，基于矩阵提出一种可以在对象和属性同时增加的情况下有效更新的增量方法.Huang et al［16］将近似集的布尔矩阵表示方法引入动态模糊信息系统，考虑属性和对象增加的情况，通过更新布尔矩阵达到动态更新近似集的目的.Sang et al［17］将条件熵引入序决策信息系统，在系统中添加或删除多个对象时，基于矩阵提出两种增量属性约简算法，还针对动态变化的有序模糊信息系统的特征选择（属性约简）问题，提出一种新的模糊优势邻域粗糙集模型，并基于条件熵提出一种启发式增量特征选择（属性约简）算法［18］.上述研究推动了序决策信息系统近似集的动态更新在众多领域的发展，但是，针对属性集动态变化的序决策信息系统，基于矩阵计算其属性约简的增量算法并不常见.

本文以序决策信息系统为研究对象，首先将王磊和李天瑞［19］的知识粒度的矩阵表示与计算方法推广到序决策信息系统中，同时，将经典粗糙集中以知识粒度表征的属性重要度为启发信息的属性约简方法引入优势粗糙集方法，作为本文的非增量对照实验算法.然后，以矩阵分析序决策信息系统中知识粒度、劣势元素矩阵和优势关系矩阵在属性数目变化条件下的变化过程，并给出属性增删条件下属性约简的增量更新机制，基于此提出两种新的增量属性约简算法.最后，在UCI数据集上测试了属性约简算法的性能，实验结果证实了本文提出的增量属性约简算法的可行性和高效性.

本文提出的劣势元素矩阵和优势关系矩阵的增量更新机制能降低属性约简子集选取属性的计算成本，进一步增加算法的增量属性约简效率，同时，其不仅适用于序决策信息系统，还可扩展到其他模型的属性约简算法.究其本质，劣势元素矩阵和优势关系矩阵的增量更新机制的提出，给出了基于满足模型关系和不满足模型关系相结合的属性约简方法.

1 基本知识

首先介绍优势粗糙集方法的相关基础知识，然后，将知识粒度的矩阵表示与计算方法扩展到优势粗糙集方法中，介绍了以知识粒度为启发信息的启发式属性约简算法.

1.1 优势粗糙集方法的相关基础知识

定义1决策信息系统S=(U，A=C∪D，V，f)，其中，U为非空有限对象集合，U={x1，x2，…，xm}；A是一个有限非空属性集，C是条件属性集，D是决策属性集，并且C∩D=∅；对于∀a∈A，均存在a的一个属性值集Va，V=∪Va为属性集A的属性值集；f为信息系统的信息函数，能给出属性集A在U上的属性值集.若属性值集V具有偏序关系，则称该系统为序决策信息系统.

1.2 优势粗糙集方法中的启发式非增量属性约简算法根据Jing et al［20］的经典粗糙集中基于知识粒度的属性约简算法，将其引入优势粗糙集方法，构造以知识粒度表征的属性重要度为启发信息的属性约简算法，如算法1 所示.

然而，对属性集动态变化的数据集进行属性约简时，算法1 会重新计算变化后的数据集，这会重复计算上次的属性约简结果，极大地提升属性集动态变化数据集的属性约简时间复杂度.此外，在步骤5 和步骤7 中增加或者删除某个属性后，需要重新计算更新对应的优势关系矩阵，重新判断对象在未变化属性上的优势关系，很大程度上降低了算法属性约简的效率.针对这些问题，本文研究了属性集变化下属性约简的增量更新机制，包括知识粒度的矩阵增量更新方法、优势关系矩阵的增量更新方法和劣势元素矩阵的增量更新方法，基于此设计了启发式增量属性约简算法.

2 属性集变化下序决策信息系统的增量属性约简算法

为了提高属性集动态变化的数据集的属性约简效率，通过矩阵分析序决策信息系统中知识粒度在属性数目变化条件下的增量更新机制，进一步分析优势关系矩阵和劣势元素矩阵的增量更新机制，最后在属性集增加和属性集删除的条件下，分别设计了两种启发式增量属性约简算法.

2.1 属性集增加条件下的增量更新机制

定理1给定一个序决策信息系统S=(U，A=C∪D，V，f)，P⊆C，Q是新增的属性集，GK(P)为属性集P的知识粒度，那么新增属性集后更新的知识粒度为：

2.2 属性集删除条件下的增量更新机制

此外，当删除或者增加属性集Q时，U在属性集P-Q，P∪D-Q，P∪Q和P∪Q∪D上的劣势属性矩阵元素都会发生相应的增量变化，具体表示为：

定理4给定一个序决策信息系统S=(U，A=C∪D，V，f)，Q⊆P⊆C，Q是S删除的属性集，GK(P)为属性集P的知识粒度，那么新增属性集后更新的知识粒度为：

证明过程与定理2 的证明过程类似，略.

2.3 属性集变化条件下的增量属性约简算法基于2.1 和2.2 的知识粒度和优势关系矩阵的增量更新机制，属性集变化下增量属性约简算法的过程主要分三个步骤：

（1）对属性集变化的数据集增量更新其相对知识粒度；

（2）向约简集中添加待约简集中外部属性重要度最大的属性；

（3）逐步向前删除约简集中的冗余属性，提高约简结果的准确性.

属性集变化下的增量属性约简算法如算法2和算法3 所示.

2.4 三种算法的时间复杂度分析表1 给出了数据集属性增加时ARKG-DR 和IARAI-DR 两种算法的时间复杂度.

表1 属性增加时两种算法的时间复杂度比较Table 1 Time complexity of the two algorithms with the increase of attributes

由以上分析可知，被约简集C的属性越多，IARAI-DR 和ARKG-DR 算法相比，效率更高.

表2 给出了数据集属性删除时IARAD-DR和ARKG-DR 两种算法的时间复杂度.

表2 属性删除时两种算法的时间复杂度比较Table 2 Time complexity of the two algorithms with the deletion of attributes

由以上的分析可知，被约简集C的属性越多，IARAD-DR 和ARKG-DR 算法相比，效率更高.

3 实验与结果分析

为了验证算法2 和算法3 的有效性及属性约简结果的准确性，从UCI 机器学习数据库（https：∥archive.ics.uci.edu/ml/datasets.php）中选取六个数据集进行算法的性能测试.实验前对原始数据进行以下预处理：对属性值为字符串的数据集，根据数据集属性信息将字符串属性值按从劣到优的趋势赋予从小到大的具体数值，且相同的字符串属性值赋予相同数值，对属性值为数值的数据集不作任何更改，此外，数据集的分类（决策）属性值若相同则赋予相同的具体数值.各UCI 数据集信息的具体描述如表3 所示.

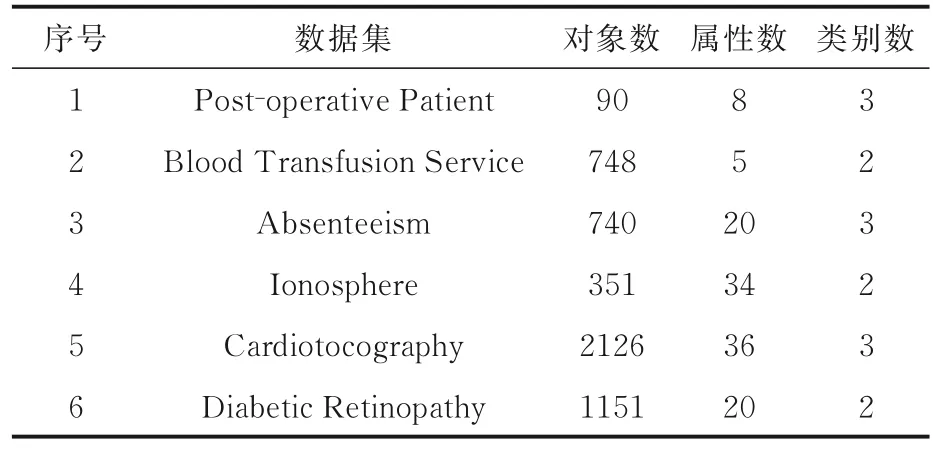
表3 实验使用的UCI 数据集Table 3 UCI datasets used in experiments

测试环境：Intel（R）Core（TM）i5-6300HQ CPU @ 2.30 GHz 处理器，12 GB 内存，操作系统为Window10（64 位），Pycharm 软件平台.

实验分三部分.首先，将各数据集的数据按属性分为五等份，将第一份数据作为基础数据集，每次添加一份数据直至将整个数据集添加进来进行属性约简，最后比较分析IARAI-DR 和ARKGDR 算法按此过程对数据集进行属性约简的运行时间和属性约简结果.第二部分，将第一部分实验得出的数据作为已知条件，将整个数据集作为基础数据集，每次从后往前删除一份数据直至还剩最后一份数据进行属性约简，然后比较分析IARAD-DR 算法按此过程对数据集进行属性约简和第一部分ARKG-DR 算法属性约简的运行时间.前两部分实验中的属性约简运行时间是十次运行时间的均值.第三部分，在Weka 机器学习软件上测试IARAI-DR 和ARKG-DR 算法在六个数据集上属性约简的分类准确度.

从表3 可知，实验选取了六个不同规模的数据集.规模最大的是Cardiotocography 数据集，有2126 个对象、36 维属性，规模最小的是Post-operative Patient 数据集，仅有90 个对象、8 维属性；属性维数最多的是Cardiotocography 数据集，有36维属性，属性维数最少的是Blood Transfusion Service 数据集，具有5 维属性.

图1 给出了逐渐增加数据时，ARKG-DR 和IARAI-DR 算法的运行时间.由图可见，数据量属性占比为20%时，ARKG-DR 和IARAI-DR 算法处理各数据集的运行时间的差距不大，这是因为属性较少时，两者的时间复杂度差距不大；随着数据量的增加，增量算法IARAI-DR 处理各数据集的运行时间明显少于静态算法ARKG-DR.总体上，增量算法IARAI-DR 计算数据集属性约简的运行效率优于ARKG-DR 算法.

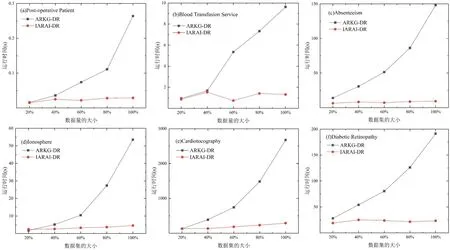
图1 数据量逐渐增加时，ARKG-DR 和IARAI-DR 算法运行时间的比较Fig.1 Running time of ARKG-DR and IARAI-DR algorithms with the increase of data amount

表4 给出了ARKG-DR 和IARAI-DR 算法在各数据集上计算属性约简的结果.由表可见，IARAI-DR 处理Absenteeism 数据集的属性约简结果长度优于ARKG-DR 算法，处理其余数据集的属性约简结果的长度与ARKG-DR 算法一致.

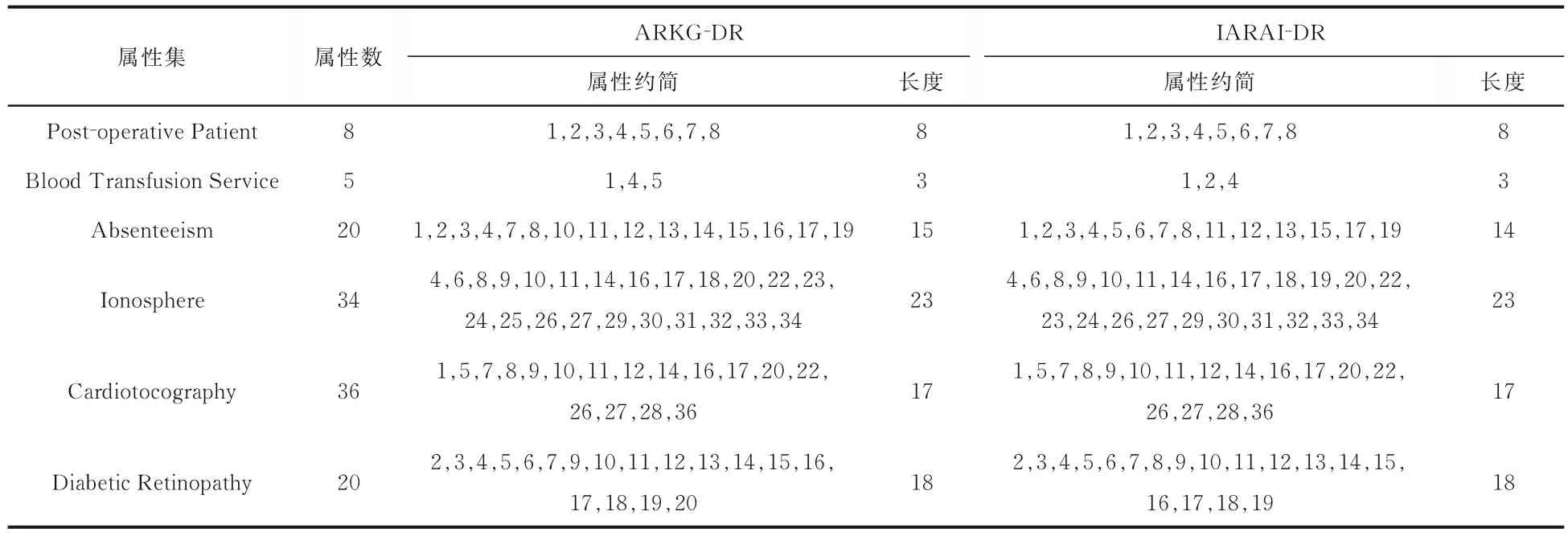
表4 两种算法在六个数据集上属性约简结果的比较Table 4 Attribute reduction results of two algorithms on six datasets

图2 给出了从后往前逐渐删除数据时，ARKG-DR 和IARAD-DR 算法处理数据集的运行时间.由图可见，当数据的删除量从0 增加到80%时，增量算法IARAD-DR 处理各数据集的运行时间都少于ARKG-DR 算法；当数据的删除量接近或高于80%时，增量算法IARAD-DR 处理各数据集的运行时间与ARKG-DR 算法差不多.总体上，增量算法IARAD-DR 计算数据集属性约简的运行效率优于ARKG-DR 算法.

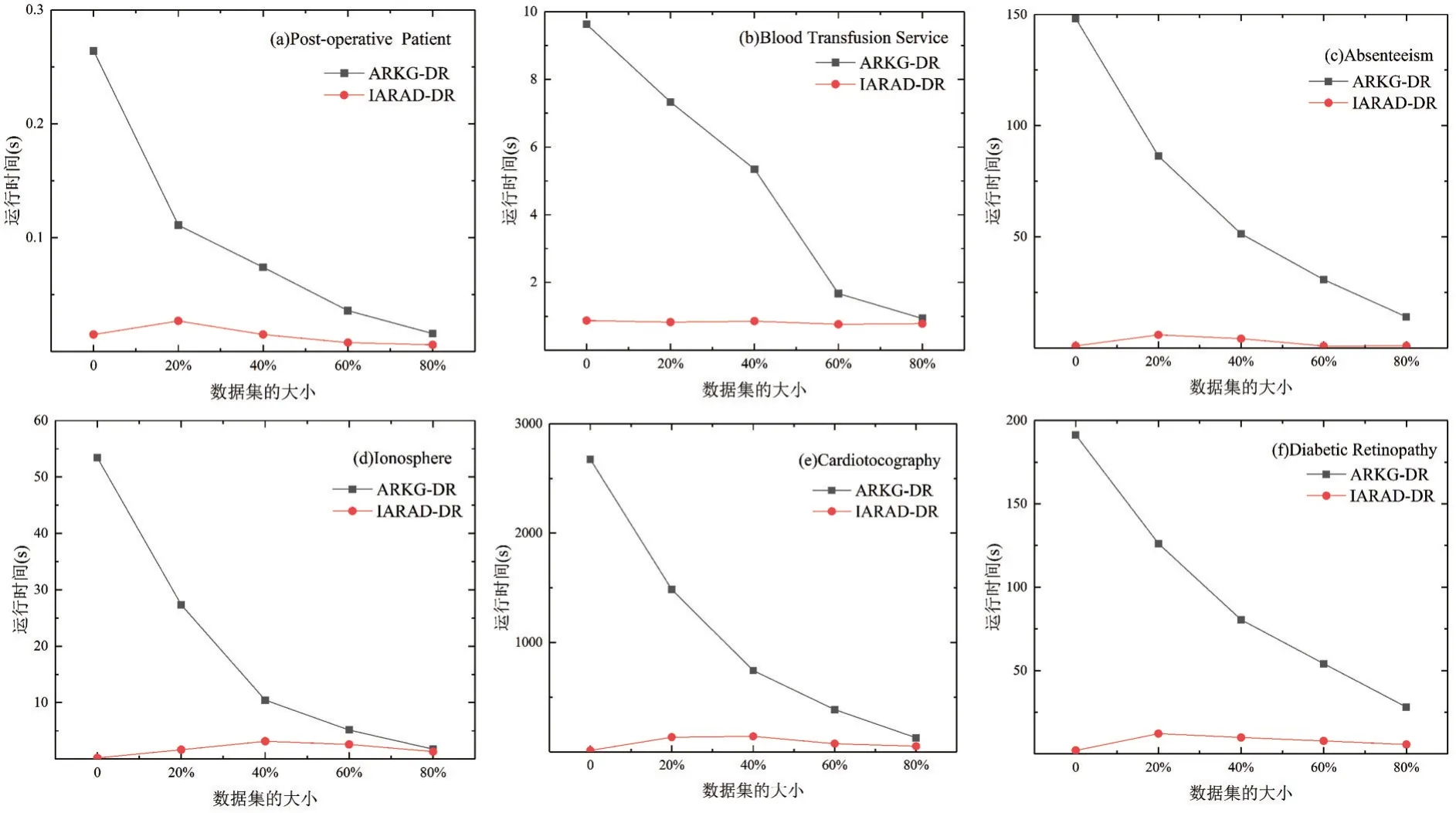
图2 从后向前删除数据时，ARKG-DR 和IARAD-DR 算法运行时间的比较Fig 2 Running time of ARKG-DR and IARAD-DR algorithms with the deletion of data from back to front

为了验证ARKG-DR 和IARAI-DR 算法处理各数据集得到的属性约简结果的准确性，使用Weka 机器学习软件上自带的贝叶斯分类器进行测试并使用十折交叉验证的方式计算ARKG-DR和IARAI-DR 算法得到的属性约简结果的分类准确度，结果如表5 所示.由表可见，IARAI-DR 在大多数数据集上的分类准确度和ARKG-DR 算法一致，在Absenteeism 和Ionosphere 数据集上稍优于ARKG-DR 算法，可见IARAI-DR 算法计算属性约简是有效且准确的.

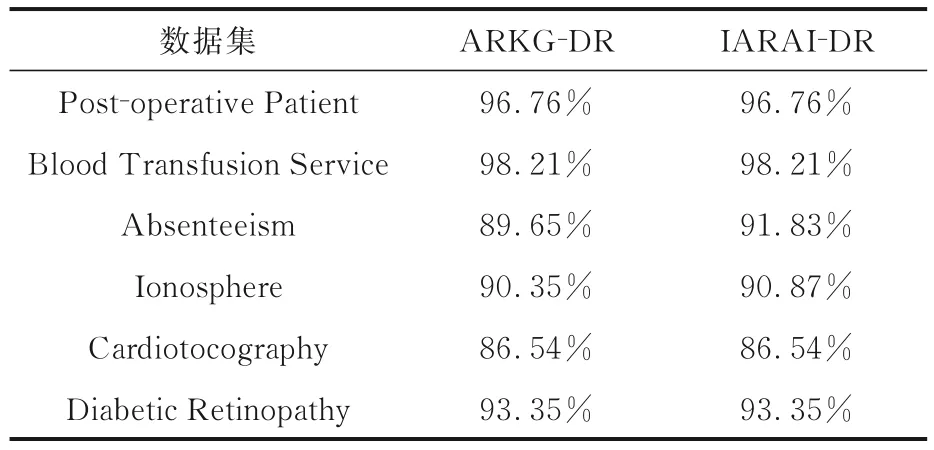
表5 ARKG-DR 和IARAI-DR 算法在六个数据集上的分类准确度的比较Table 5 Classification accuracy of ARKG-DR and IARAI-DR algorithms on six datasets

4 结论

本文以知识粒度来度量序决策信息系统中的属性重要度，并以矩阵分析序决策信息系统中属性增删条件下知识粒度和优势关系矩阵的增量更新机制，由此提出了两种以属性重要度为启发信息的增量属性约简算法.为了验证算法的有效性和高效性，选择了六个UCI 数据集进行实验.实验结果表明：从属性约简效率的角度看，各数据集参与属性约简的属性数目越多，本文提出的两种增量属性约简算法明显优于非增量约简算法；从属性约简结果的准确性看，本文提出的两种增量属性约简算法与非增量约简算法相差不大.另外，现实生活中的数据样本随时会发生动态变化，本文提出的算法无法对其进行属性约简.未来研究的重点是在序决策信息系统中有多个对象增加或者删除的情况下，设计以知识粒度表征属性重要度的快速增量式属性约简算法.