卷积神经网络与人工水母搜索的图特征选择方法

孙林 ,蔡怡文

（1.河南师范大学计算机与信息工程学院，新乡，453007；2.天津科技大学人工智能学院，天津，300457）

随着大数据技术的迅猛发展，众多领域中的超高维数据往往包含大量的冗余信息和噪声，大大降低了学习算法的分类性能［1］.特征选择旨在使用一些标准来选取最优特征子集，去除冗余特征［2］，许多研究者也将仿生优化与特征选择相结合.例如，Jia et al［3］提出一种新的混合海鸥优化的特征选择算法，但在实际数据集上进行特征选择的效果不好，结果较差.Peng et al［4］提出一种基于蚁群优化的改进特征选择算法，虽然大幅提升了贝叶斯过滤器的性能，但整体提升效果较差.Xue et al［5］通过生成非主导解（特征子集）的帕累托前沿解将非支配排序的思想引入粒子群算法来解决特征选择问题，但其收敛效果还有待提升.人工水母搜索（Artificial Jellyfish Search，AJS）算法是2020 年Ezzeldin et al［6］提出的一种新型优化算法，其模拟水母的搜寻行为，与蚱蜢算法、蝗虫算法相比，其寻优能力更强，收敛速度更快.水母跟随洋流运动，水母群的运动分主动和被动两种，它们之间的运动切换以及它们汇聚成水母簇的过程由时间控制机制来控制.目前尚未见结合人工水母搜索的特征选择方法.

图嵌入是一种将高维数据转化为低维向量的表示方法［7］，可以运用在人脸识别、无人机自组网链路预测、知识图谱等方面［8］，目前已有的图嵌入算法［9］主要包括基于神经网络的图嵌入、基于网络拓扑结构的图嵌入等.图像分类中图片的特征通常是高维的、复杂的，可能会出现由于特征维度过高而导致提取的特征在进行分类时准确率不高的问题，现有很多图嵌入降维方法.例如，颜伟泰［10］提出一种基于局部保持的图嵌入监督降维方法，但其依赖于完整的类别以及平衡因子.张晓语［11］提出一种基于矩阵分解的多视图降维算法，但不能有效处理大规模数据.在图像分类过程中特征选择是一个挑战［12］，大多数研究者使用卷积神经网络（Convolutional Neural Network，CNN）来进行图像分类，既可以减少特征数量，又能增加图像分类的精度.现在已有大量CNN 以及改进的神经网络用于图像分类.例如，周衍挺［13］提出一种改进的卷积神经网络，孙克雷等［14］提出一种基于改进Softplus 激活函数的卷积神经网络模型，刘梦雅和毛剑琳［15］提出一种基于最大池化和平均池化的改进池化模型.这些CNN 虽然能对高维数据进行特征提取，但分类精度仍然不高.

当前，数据大多以图像的形式展现出来，选择特征时就会忽略图数据之间的信息.为了解决这个问题，基于进化计算的图特征选择将特征选择问题转化为特征图的遍历问题［16］，目前，这一新颖的研究思路仍有待改进和提高.CNN 能够有效地从大量样本中学习到相应的特征，避免复杂的特征提取过程，图嵌入算法能够很好地捕捉图的拓扑结构，AJS 算法寻优能力强，收敛速度快，因此，本文将图嵌入算法和AJS 算法引入CNN 模型，构建了一种基于CNN 与AJS 的图特征选择方法.

本文的主要贡献：（1）根据特征图中节点权重改进图嵌入算法中的随机游走节点概率，增大权重大的节点的游走概率，进而去除冗余特征，使模型的分类准确率得到提升；（2）在AJS 算法的位置更新公式中引入余弦相似度，通过调整权重来控制搜索空间，提高算法的收敛速度；（3）将改进后的图嵌入算法和AJS 算法与CNN 进行结合，通过基准函数和数据集上的实验，证明其分类准确率、收敛速度和寻优精度均得到有效提升.

1 基础理论

1.1 卷积神经网络CNN［17］主要用来探索图像数据，其结构包括输入层、隐藏层和输出层，隐藏层又包括卷积层、池化层和全连接层.CNN 是深度学习的主要算法之一［18］.卷积层的计算如下：

其中，X={xi，j|i=0，…，n；j=0，…，m}为输入图像，n和m分别为图像的行和列，W为卷积核权重，b为偏置.

输入图像X，卷积核为k，填充p行和p列，则经过卷积层后输出的形状为Xn×m，其中n和m分别为：

其中，h为行，w为列，n为输入数据的行数，m为输入数据的列数，kh为卷积核的行数，kw为卷积核的列数，ph为填充的行数，pw为填充的列数.

池化层［19］只对池化窗口中的元素进行运算，假设{X1，X2，…，Xd}为池化窗口中的元素池化，则最大池化的运算如下：

其中，Xi为池化窗口中的第i个元素，i=1，2，…，d，Y为输出，Max()为求最大值的函数.

ReLU 函数［20］是一种线性不饱和的激活函数，其计算如下：

1.2 人工水母搜索在群体内部移动的水母被称为A 类水母，跟随洋流运动的水母被称为B 类水母.A 类水母的位置更新为：

其中，Xi为第i个水母的位置，t为迭代时间，Ub和Lb为搜索空间的上限和下限，γ为运动系数.

B 类水母是被动运动，会朝着食物多的方向移动.B 类水母的运动方向为：

时间控制如下式所示：

其中，t为迭代次数，Maxiter为最大迭代次数.

2 图特征选择方法

Node2Vec［21］的组合方式是通过两个参数p和q进行正则化，q定义了随机游走通过图中之前未见节点的概率，p和q参数需要根据情况自行设置.q的计算如下：

其中，d为节点总数，walk为已经遍历过节点的总数，WVi为节点Vi的权重.

Node2Vec 学习嵌入的转移概率为：

其中，g代表上一个节点，Vi表示当前节点，Vj代表下一个准备访问的节点，dg，Vj表示上一个节点与待访问节点的距离，dg，Vj=0 代表当前节点返回上一个节点，即g→Vi→g.

2.2 基于余弦相似度的人工水母搜索在水母的位置更新中引入一个余弦相似度，人工水母群A 类型运动的人工水母围绕它们自己的位置运动.余弦相似度的计算为：

其中，Maxiter为最大迭代次数，t为当前迭代次数.在人工水母更新位置增加余弦值，于是，A 类人工水母的位置更新为：

其中，Ub和Lb为搜索空间的上限和下限，γ为运动系数.

2.3 图特征选择算法描述将CNN 与图嵌入算法和AJS 算法相结合，设计图特征选择算法.首先，将数据集输入卷积层，从卷积层输出后进入池化层，进行三次卷积和三次池化，将输出的图像构建成图数据，再将构建好的特征图根据图嵌入进行降维得到一个二维向量；然后，利用水母优化算法初始化种群，进行特征选择，在进行特征选择时，选择固定个数的特征；最后，将特征输入分类器进行模型训练以及评估.其算法伪代码的具体步骤如算法1 所示.

依据上述图特征选择模型，将余弦值加入A 类水母的位置更新，设计基于余弦相似度的AJS 算法（Artificial Jellyfish Search Algorithm Based on Cosine Similarity，CSAJS），如算法2 所示，其伪代码如下.

在GEARW 和CSAJS 的基础上，设计基于CNN 与AJS 算法的图特征选择算法（Convolutional Neural Network and Artificial Jellyfish Search-Based Graph Feature Selection Algorithm，CAGFS），具体过程如算法3 所示.

3 实验结果与分析

3.1 数据集与实验准备为了评估改进算法的效果，实验分两部分：（1）从文献［22］中选择10 个基准函数进行算法的优化性能测试，测试函数的详细信息如表1 所示；（2）从Python 的torchvision.datasets 中选择四个公共数据集MNIST，EMNIST，KMNIST 和FashionMNIST 进行特征选择测试与分析，具体内容如表2 所示.

表1 10 个基准测试函数的描述Table 1 Description of ten benchmark test functions

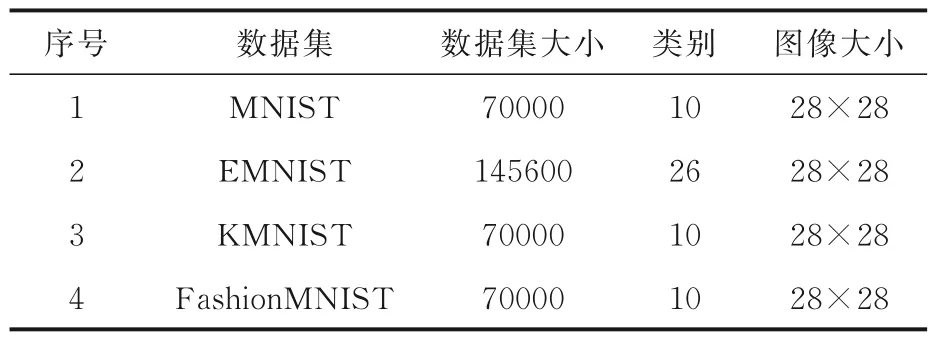
表2 实验使用的四种数据集Table 2 Four datasets used in experiments

为了测试算法在四个数据集上的分类性能，采用交叉熵损失、整体交叉熵损失［23］、平均分类准确率（Average Classification Accuracy，AccAvg）、精确率、召回率和F1-score 进行测试.整体交叉熵损失由交叉熵损失与样本数量相乘得到，与数据集的大小有关，数据集大，则整体交叉熵损失较大，数据集小，则整体交叉熵损失较小.

操作系统及环境：Windows 7，Python 3.7.4；框架Pytorch 1.9.1；CPU Intel（R）Corr（TM）i5-6500.为了避免实验结果的随机性，确保实验结果的公平性，所有对比算法均运行20 次，取其结果的平均值.将本文的CAGFS 算法与三种算法进行对比实验，分别是传统的CNN 模型［24］、LeNet模型［25］和基于平均池化的LeNet 模型（LeNet Model Based on Average Pooling，AVGLeNet）［26］.改进后的CAGFS 模型的网络参数如表3 所示，四种模型均采用SGD 优化器，学习率设置为3e-2，批量大小设置为128.

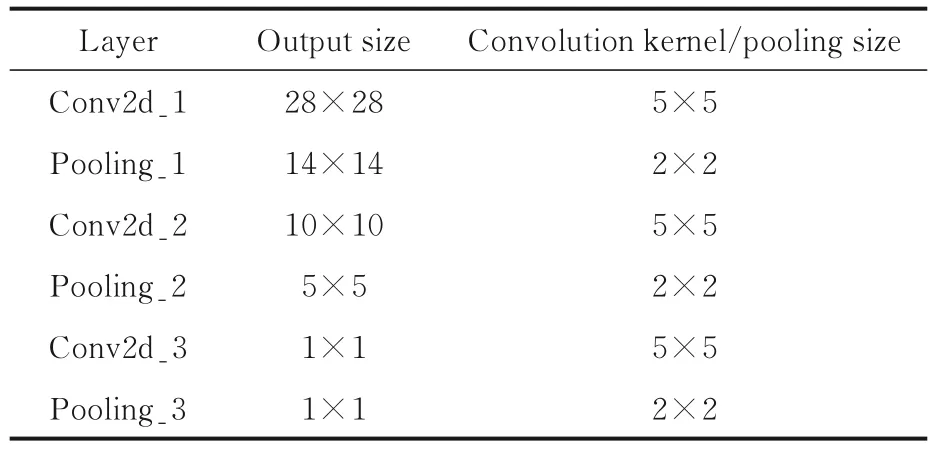
表3 改进后的网络参数Table 3 Improved network parameters

3.2 优化性能分析为了检验本文CSAJS 算法的优化性能，分别将CSAJS 算法、原始的AJS 算法［6］、原始的鲸鱼优化算法（Whale Optimization Algorithm，WOA）［22］、海洋捕食者算法（Marine Predators Algorithm，MPA）［27］、闪电搜索算法（Lightning Search Algorithm，LSA）［28］和水循环算法（Water Cycle Algorithm，WCA）［29］在10 个基准测试函数上进行寻优.种群规模设置为30，种群维度设置为30，迭代次数Niter=500，其余参数均采用对应文献中的最佳实验参数，独立运行20次.为了测试上述六种算法的优化性能，采用最优值（Best）、最差值（Worst）、平均值（Mean）和标准方差（Standard Deviation，STD），来评判算法的寻优精度.最优值反映算法最好的寻优精度，最差值反映算法最差的寻优精度，平均值反映算法的平均寻优精度，标准方差反映算法的寻优稳定性，实验结果如表4 所示.实验数值越小，效果越好.由表可见，与其他五种算法相比，CSAJS 算法的优化性能较好，在f1～f4和f6这五个函数上均优于其他五种算法，寻优精度提高了1～10 个数量级；在f5函数上，CSAJS 算法的STD略低于MPA算法；在f7函数上，CSAJS 算法的Mean和STD略低于AJS 算法；在f8函数上，CSAJS 算法的四种指标均略低于AJS 算法；在f9和f10函数上，CSAJS 算法的Best，Worst和Mean均略低于其他算法，但是其STD优于其他四种算法，说明其寻优效果更稳定，可能是增加权重导致搜索范围扩大造成的.整体来看，CSAJS 算法的寻优精度和稳定性均高于其他算法.

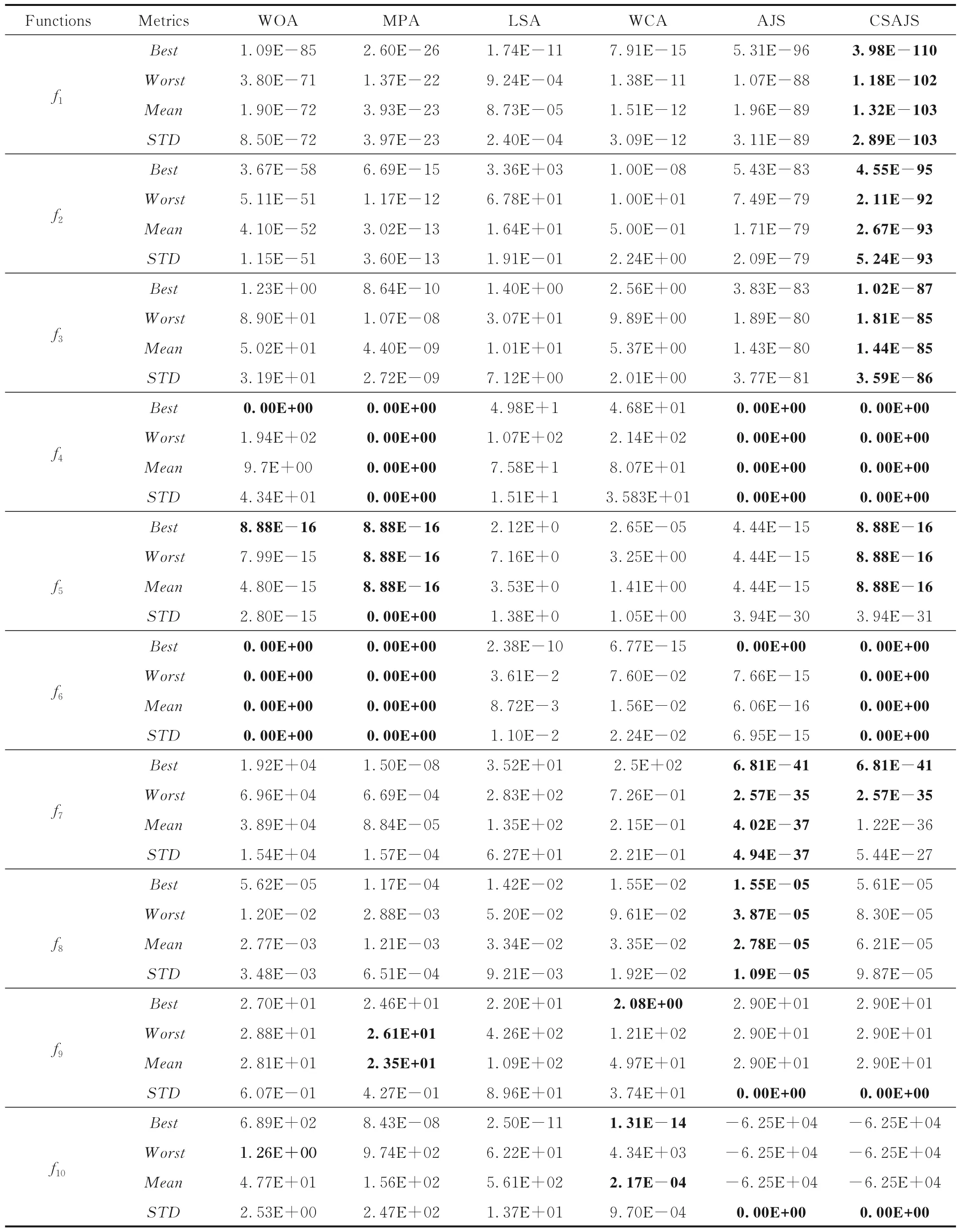
表4 六种算法在10 个基准测试函数上的四种评价指标的对比Table 4 Four metrics of six algorithms on ten benchmark test functions

图1 展示了六种算法在10 个基准函数上的寻优收敛曲线.由图可见，在f1～f6上CSAJS 算法的收敛速度较快，寻优效果也比其他五种算法好，有效减少了迭代次数.但是，在f2，f6和f8上，CSAJS算法陷入了局部最优，分别在迭代150，150 和250次时达到最优.在f1，f4和f5函数上，CSAJS 算法的收敛速度更快，分别在迭代50，50 和100 次时达到最优.在f7和f8函数上，CSAJS 算法的收敛速度略低于AJS 算法.在f9和f10函数上，CSAJS 算法的收敛速度与AJS 算法基本一致，收敛效果也基本一致.由于在f10函数上的算法寻优图像差距较大，无法完全显示，所以截取迭代前30 次的部分图像，这可能是搜索范围扩大造成的.

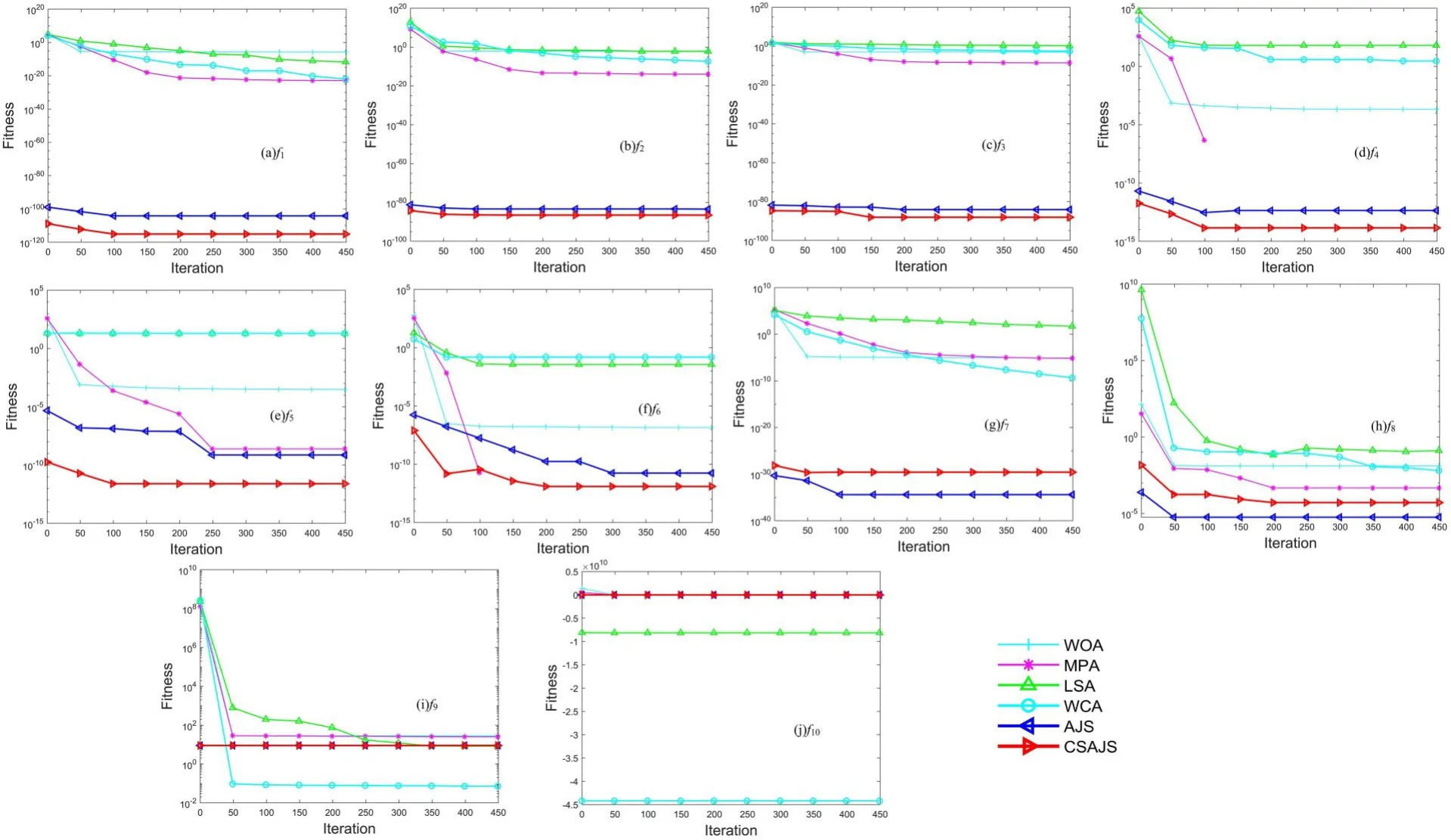
图1 六种优化算法在10 个基准测试函数上的收敛曲线Fig.1 Convergence curves of six optimization algorithms on ten benchmark test functions

整体来看，CSAJS 算法的收敛速度优于其他算法，而且能有效减少迭代次数.

3.3 数据集实验结果为了验证改进算法的有效性和分类效果，将CAGFS 算法与其他三种算法在四个数据集上进行对比实验.训练集中单个样本的交叉熵损失如表5 所示，表中黑体字表示结果最优.测试集上的整体交叉熵损失如图2 所示.

图2 提出的CAGFS 模型在四个数据集上的整体交叉熵损失Fig.2 Overall cross entropy loss of the proposed CAGFS model on four datasets

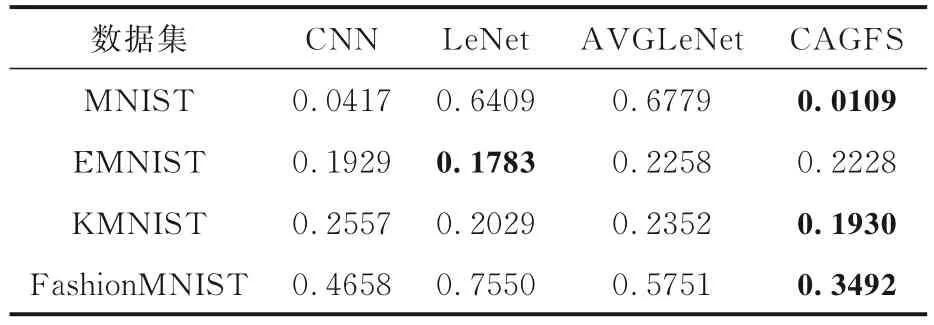
表5 四种算法在四个数据集上的交叉熵损失Table 5 Cross entropy loss of four algorithms on four datasets

由表5 可见，在MNIST 数据集上，CAGFS 模型的交叉熵损失最小，说明其训练效果较好.在EMNIST 数据集上，LeNet 模型的交叉熵损失最小，CAGFS 模型的交叉熵损失排第三位，因为EMNIST 数据集的数据类别比较高，进行特征选择时选出的特征较少，分类效果较差.在KMNIST数据集上，CAGFS 模型的交叉熵损失最小，CNN模型的交叉熵损失最大，说明CNN 模型在增加特征选择后可以提升分类效果.在FashionMNIST数据集上，CAGFS 模型的交叉熵损失最小，说明改进的CAGFS 模型的分类效果较好.

由图2 可以看出，在MNIST 数据集上，CAGFS 模型的整体交叉熵损失的收敛速度较快而且整体交叉熵损失较小，在12 轮之后逐渐平稳.在EMNIST 数据集上，CAGFS 模型虽然收敛较快，但是整体交叉熵损失较大，20 轮之后的整体交叉熵损失达到70 左右.在KMNIST 数据集上，CAGFS 模型的收敛速度相对较慢，20 轮之后整体交叉熵损失在50 左右.在FashionMNIST数据集上，CAGFS 模型的整体交叉熵损失收敛最慢，收敛曲线较平滑，20 轮之后的整体交叉熵损失在55 左右.总体来看，CAGFS 模型在四个数据集上的整体交叉熵损失逐渐减小，说明模型效果较好.CAGFS 模型的整体交叉熵损失在MNIST 数据集上最小，在EMNIST 数据集上最大，可能是EMNIST 数据集的类别较多的缘故，说明该模型更适用于类别较少的数据集.

图3 展示了四种算法在四个测试集上的AccAvg随着训练轮数增加的变化情况.图3a 为MNIST 数据集上的实验结果，可以看出，CNN 和CAGFS 的AccAvg在经过20 轮训练之后在97%左右；LeNet 的AccAvg变化不大，一直稳定在80%左右；AVGLeNet 的效果最差，AccAvg最高为45%；CAGFS 的AccAvg更高一些.图3b 为EMNIST 数据集上的实验结果，四种模型经过20 轮的训练，AccAvg都达到90%.在前四轮训练中，CNN 的效果较好，CAGFS 次之，说明对于类别较多的数据集，CAGFS 的特征选择的效果不是最佳.图3c为KMNIST 数据集上的实验结果，可以看出，在前三轮训练中，CAGFS 的AccAvg最高，但训练三轮后CNN 的AccAvg高于CAGFS，训练10 轮后四个模型的AccAvg逐渐趋于平稳，达到基本一致.说明经过对优化算法的改进，CAGFS 明显在训练前期提高了算法的分类精度.图3d 为Fashion-MNIST 数据集上的实验结果，可以看出，在前两轮训练中CNN 的AccAvg上升较快，CAGFS 的AccAvg在前两轮训练中比CNN 高，之后则略低于CNN 模型；第17 轮训练时，CAGFS 的AccAvg上升到90%，而后上下浮动并趋于稳定；AVGLeNet和LeNet 的AccAvg稳定在75%.

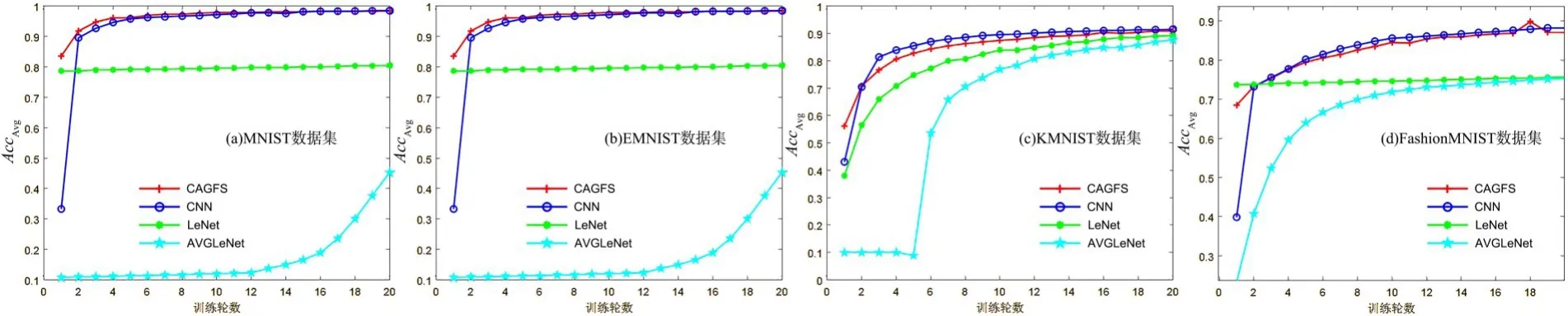
图3 四种算法在四个数据集上的AccAvgFig.3 AccAvg of four algorithms on four datasets

综上，CAGFS 模型有效地提高了其在数据集上的分类精度，尤其在类别较少的数据集上，效果比在类别多而特征数量少的数据集上要好.

四种算法在四个训练集上的AccAvg如表6 所示，表中黑体字表示结果最优.由表可见，在MNIST 数据集上，CAGFS 的AccAvg比其他三种模型分别高3.1%，21% 和79.7%.在EMNIST数据集上，CAGFS 的AccAvg比CNN 低2.2%，这是由于CAGFS 在图嵌入过程中去掉了一些权重较大的特征，导致分类结果不准确，但其AccAvg比其他两种模型分别高2%和5%.在KMNIST 数据集上，CAGFS 的AccAvg比其他三种模型分别高0.2%，9.8% 和27.5%.在FashionMNIST 数据集上，CAGFS 的AccAvg比其他三种模型分别高1.3%，8.4%和16.7%.

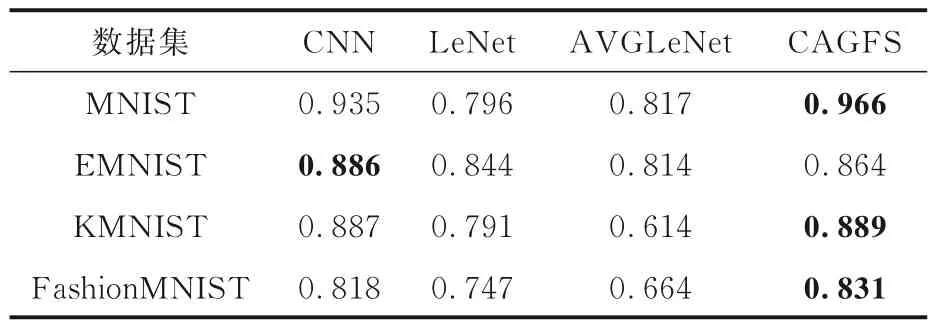
表6 四种算法在四个数据集上的AccAvgTable 6 AccAvg of four algorithms on four datasets

表7 是四种模型在四个数据集上训练20 轮的精确率，表中黑体字表示结果最优.由表可见，在MNIST 数据集上，CAGFS 的精确率比其他三种模型分别高2.0%，1.1%和1.7%.在EMNIST数据集上，CAGFS 的精确率比CNN 和LeNet 分别低2.0% 和7.4%.在KMNIST 数据集上，CAGFS 的精确率比其他三种模型分别高5.8%，1.3% 和2.4%.在FashionMNIST 数据集上，CAGFS 的精确率比其他三种模型分别高14.3%，1.5%和5.6%.

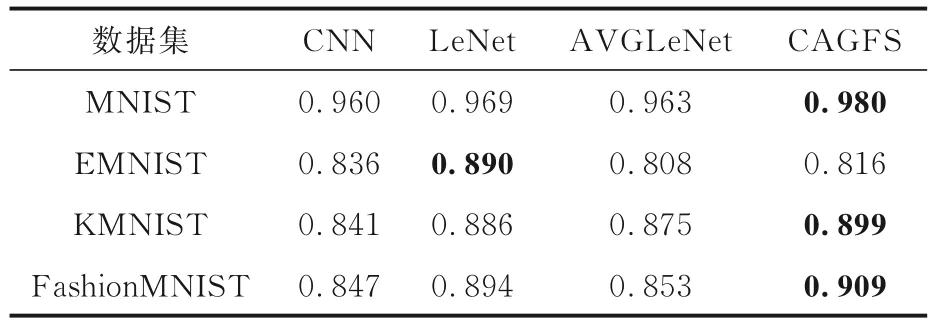
表7 四种算法在四个数据集上的精确率Table 7 Accuracy rates of four algorithms on four datasets

表8 是四种模型在四个数据集上训练20 轮的召回率，表中黑体字表示结果最优.由表可见，在MNIST 数据集上，CAGFS 的召回率比其他三种模型分别高1.5%，1.5%和1.5%.在EMNIST数据集上，CAGFS 的召回率比其他三种模型分别低3.1%，10.1%和7.8%.在KMNIST 数据集上，CAGFS 的召回率比AVGLeNet 低7.9%.在FashionMNIST 数据集上，CAGFS 的召回率比其他三种模型分别高6.2%，1.0%和2.1%.

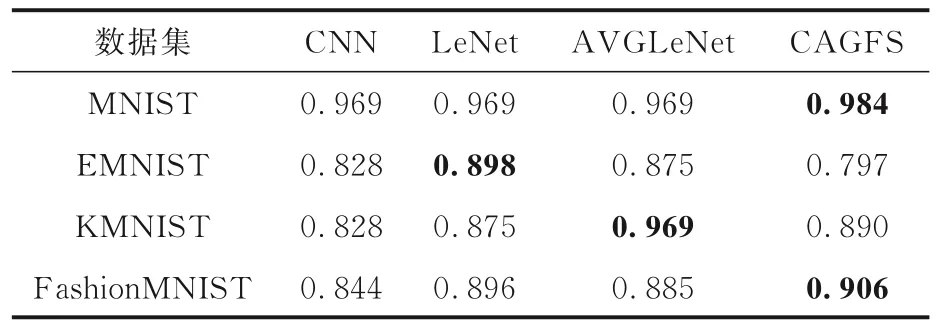
表8 四种算法在四个数据集上的召回率Table 8 Recall rates of four algorithms on four datasets

表9 是四种模型在四个数据集上训练20 轮的F1-score，表中黑体字表示结果最优.由于处理的是多分类问题，而且召回率和F1-score 用的是同一种方法，所以它们的计算结果一样.在MNIST 数据集上，CAGFS 的F1-score 比其他三种模型分别高1.5%，1.5%和1.5%.在EMNIST数据集上，CAGFS 的F1-score 比其他三种模型分别低3.1%，10.1%和7.8%.在KMNIST 数据集上，CAGFS 的F1-score 比AVGLeNet 低7.9%.在FashionMNIST 数据集上，CAGFS 的F1-score比其他三种模型分别高6.2%，1.0%和2.1%.

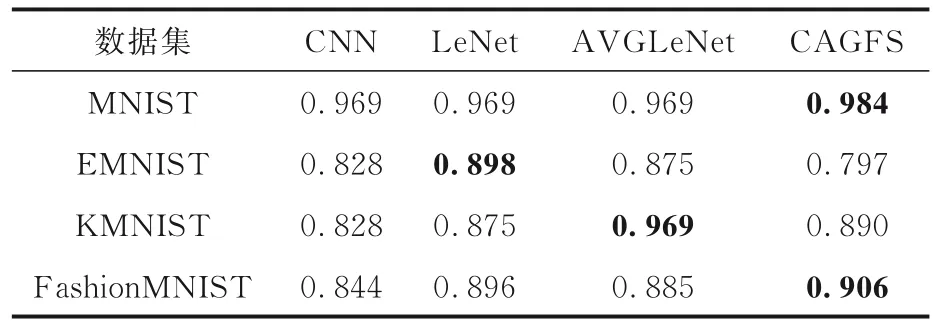
表9 四种算法在四个数据集上的F1-scoreTable 9 F1-score of four algorithms on four datasets

综上所述，CAGFS 模型的准确率、精确率、召回率和F1-score 均有一定提升，尤其对那些特征维数高、类别少的灰度图像数据集，CAGFS 模型经过降维和特征选择后，能很好地去除冗余特征，因而提升了分类准确率.

3.4 模型时间分析为了评估CAGFS 算法的模型复杂度，分别从模型大小、运算时间和模型参数量进行对比分析，如表10 所示，表中黑体字表示结果最优.模型大小指模型在运算过程中占用的计算机内存资源，包括模型参数、特征图和激活函数，根据模型的运行存储形式，可以得到具体的模型体积.运算时间指模型从训练开始到结束的时间差，这里计算的是四个数据集在同一种模型上的平均运行时间.模型参数量指模型结构保存和使用所涉及的模型权重的参数量.由表可见，CAGFS 的模型较大，因为该算法是三种模型的结合.CAGFS 的参数量大于LeNet 和AVGLeNet，但小于CNN，因为CAGFS 采了三层卷积，而LeNet 和AVGLeNet 是两层卷积，所以CAGFS 的参数量大于LeNet 和AVGLeNet，小于CNN.CAGFS 的平均运行时间最长，而其他三种算法的运行时间都较短，因为该模型是三种算法的结合，其复杂度有一定的增加.

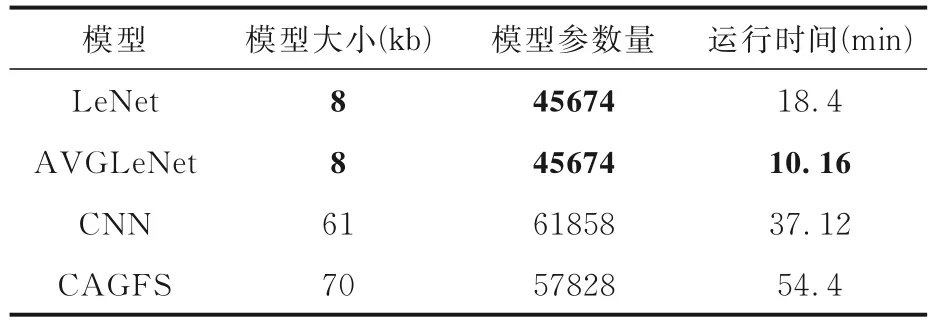
表10 四种算法的模型大小、模型参数量和运行时间Table 10 Model size，number of model parameters and running time of four algorithms

4 结论

针对特征选择收敛速度慢且分类精度不高等问题，本文提出一种由CNN、随机游走图嵌入和AJS 算法相结合的图特征选择算法.通过特征图的节点权重和边权重对图嵌入的游走概率进行改进，增加权重较大的节点特征的游走概率；利用余弦相似度改进AJS 算法的人工水母的位置，提高算法的收敛速度；设计基于CNN 与AJS 的图特征选择方法.实验结果表明，该算法在前几轮训练过程中优于其他算法，但作为三种算法的融合，该模型的复杂度较高，特别是在训练较大的数据集上的运行时间较长.由于该算法忽略了特征节点之间的相似性，所以在特征选择阶段仍然有冗余特征，因此，降低模型复杂度以及解决特征节点之间的相似性是下一步的工作.