具有否认认证的SM9标识加密算法
2023-10-29赵晨阳柯品惠林昌露
赵晨阳,柯品惠,林昌露
1.福建师范大学 计算机与网络空间安全学院,福州 350117
2.福建师范大学 数学与统计学院,福州 350117
标识加密算法(identity-based encryption,IBE)是一种特殊类型的公钥加密算法,它允许用户使用任意标识作为公钥,例如电子邮件地址、电话号码和身份证号码等。在IBE算法中,数据发送者不必获得接收者的公钥证书,即不需要公钥基础设施(public key infrastructure,PKI)。2001年,Boneh和Franklin[1]提出第一个实用且可证明安全的基于双线性对的标识加密方案。随后,研究者对标识加密算法进行了深入研究,基于双线性对提出了更多实用的IBE 算法[2-4]。虽然标识加密算法研究取得了积极进展,但标识加密算法大多以国外算法为主。为实现信息自主可控,我国自主设计了一系列中国国家标识密码标准。SM9[5]就是其中一个有代表性的密码标准,它包括3 个组成部分:数字签名算法、密钥协商算法和标识加密算法。SM9标识加密算法于2016年成为我国商用密码标准,2020 年成为国家标准。随着SM9 算法在密码技术领域占据愈来愈重要的国际地位,我国学者对SM9算法进行了深入研究,如文献[6-10]。
虽然SM9-IBE 是一个标准算法,但在一些特殊场景中,比如电子邮件系统、电子投标、电子投票和网上选举等,它不能很好地保护发送者的身份隐私。基于此,本文结合SM9算法添加否认认证协议,提出具有否认认证的SM9 标识加密算法,保护发送者的身份隐私,满足上述应用场景的现实需要。
与传统的认证协议相比,否认认证协议具有以下两个特点:(1)协议主体可以在协议运行后否认自己的参与,只有目标接收者可以验证给定消息的来源;(2)即使接收者与第三方充分合作,也不能使任何第三方相信消息是由特定的发送者发出的。
1998年,Dwork等人[11]首先提出了一个基于零知识的否认认证协议。之后,Aumann和Rabin[12]提出了另一个基于因子分解的方案,它需要一个通信双方都信任的公共目录。2001年,Deng等人[13]在Aumann和Rabin定义的模型下,分别提出了两个基于因式分解和离散对数问题的否认认证协议。2005年,Cao等人[14]利用双线性对提出了一个高效的非交互式、基于身份的否认认证协议。此外,该方案通过使用对称加密算法实现了保密性。然而,在2006 年,Chou 等人[15]指出Cao 等人的方案易遭受密钥泄露伪装(key compromise impersonation,KCI)攻击。随后Chou 等人提出了一种新的基于身份的否认认证协议,并声称该协议是安全的。然而,2007 年,Lim 等人[16]证明Chou等人的方案仍易受KCI攻击,其也是不安全的;此外,他们提出了一个增强的方案。然而在2009年,Tian等人[17]指出,Lim等人修复的协议在特殊的攻击下仍然不安全。2014年,Li等人[18]提出了一种高效的基于身份的否认认证协议。更重要的是,他们给出了其协议的安全模型和形式化证明,并声称他们的协议满足批量验证的要求,而且比所有已知的基于身份的否认认证协议更快。2015年,Wu等人[19]提出了一种高效的基于身份的否认认证加密方案,该方案在不可否认性、保密性和否认认证性均得以保证。2019年,Huang等人[20]提出了一种有效的保护隐私的否认认证加密方案,该方案在不可否认性、机密性和否认认证性的基础上对数据的完整性也提供了保证。2020 年,Kar[21]提出了一个无证书环境下的否认认证加密方案,该方案既没有密钥托管问题,也不需要公钥证书。
为了达到一定的安全性,上述方案大多基于安全参数较大的对称双线性对,并且在方案中多次使用双线性对,导致方案的计算效率下降。而SM9-IBE算法采用安全参数小的非对称双线性对,用户的公钥和私钥分别由两个不同的循环群生成,因此安全强度更高。
本文工作:首先定义SM9-DAIBE(SM9 identitybased encryption of deniable authentication)算法的安全模型,然后利用双线性对提出具体的SM9-DAIBE算法。接下来,在DBDH(decisional bilinear Diffie-Hellman)困难问题假设下,在随机预言模型中给出了算法的安全性证明。相对SM9-IBE 算法,本文提出的SM9-DAIBE算法可同时具有以下特性:
(1)保密性:该属性确保只有目标接收者可以与发送者共享所传输的消息,任何第三方都不能获得所传输的密文。
(2)否认性:消息的发送者可以在之后否认其曾传输过该消息,甚至否认参与了通信。同时,目标接收者可以识别给定消息的真实来源,但是接收者不能向任何其他第三方证明这一事实。
(3)否认认证性:该属性确保发送消息主体实际上是真正的发送者,而不是另一个第三方或对手。
1 基础知识
1.1 符号说明
设A和B为比特串,A⊕B表示A和B的按位异或运算,A||B表示A和B的级联。zP表示加法群中元素P的z倍,gr表示乘法群中元素g的r次幂。如果A是一个概率算法,那么y←A(x)表示输入x,将算法A的输出赋值给y。
表1 给出了SM9 算法中用到的密码函数的符号表示。

表1 SM9算法的函数使用说明Table 1 Description of use of functions for SM9 algorithm
1.2 双线性群
设N为素数,令G1和G2为两个N阶加法循环群,GT为N阶乘法循环群,P1和P2分别是群G1和G2的生成元。定义为双线性对映射,则应满足以下三条性质:
(1)双线性性。对于∀a,b∈[1,N-1],都有
(2)非退化性。若P1和P2不是单位元,则也不是单位元。
(3)可计算性。对于∀P1,P2,存在一个高效的多项式时间算法计算
特别地,若G1=G2,称为对称双线性群;否则称为非对称双线性群。SM9标识密码算法以非对称双线性群为构造基础。令G(1λ)表示一个双线性配对群生成算法。该算法以安全参数1λ作为输入,以元组作为输出。
1.3 基于双线性对的困难问题及假设
DBDH假设:对于任意一个概率多项式时间攻击者A,计算DBDH问题的概率都是可以忽略不计的,即Pr[0 ←A(Y)|γ=0]-Pr[0 ←A(Y)|γ=1]是可以忽略不计的。
1.4 SM9-IBE算法
本节回顾SM9-IBE 算法,该算法由以下几个步骤构成:
(2)密钥提取。给定用户的身份标识ID,密钥中心计算用户密钥deID=
(3)消息加密。对于消息M和身份标识ID,选择一个随机元素r∈,首先计算QB=Ppub-e+[H(ID)]P1,再计算密文C1=[r]QB,C2=K1⊕M,C3=Hv(C2||K2),其中K1||K2=KDF(Hv,C1||t||ID,|M|+v),t=ur。
(4)密文解密。对于密文(C1,C2,C3),首先根据私钥deID计算,再根据KDF 计算K1||K2=KDF(Hv,C1||t′||ID,|M|+v)。
若Hv(C2||K2)=C3,则返回消息M=K1⊕C2;否则,返回错误符号▲。
2 具有否认认证的SM9标识加密算法
2.1 SM9-DAIBE算法的系统模型
SM9-DAIBE算法的系统模型包含以下三个实体(见图1):
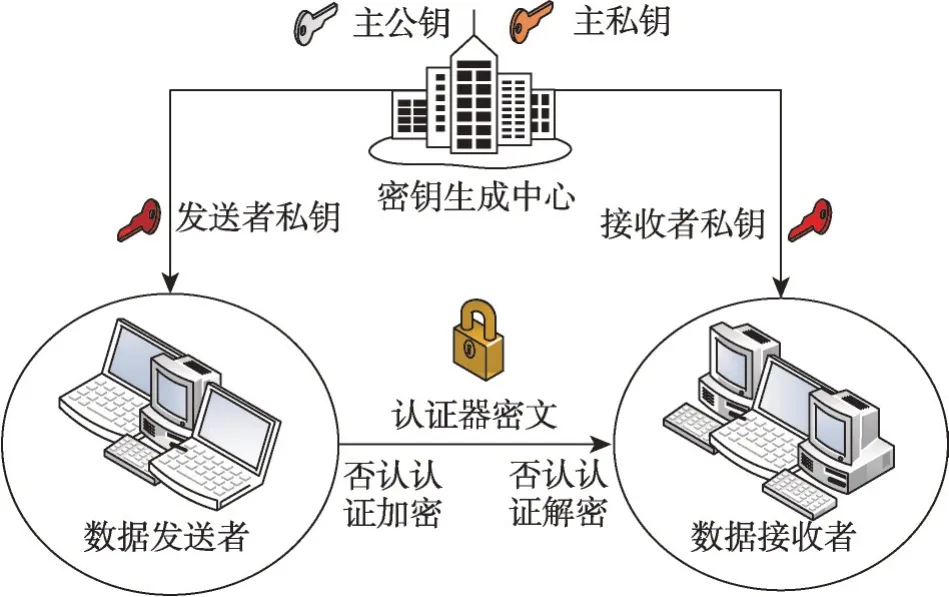
图1 SM9-DAIBE系统模型Fig.1 System model for SM9-DAIBE
(1)密钥生成中心(key generation center,KGC):负责生成系统参数和主私钥,同时为用户(包括数据发送者和数据接收者)提供私钥。
(2)数据发送者(data sender,DS):对消息进行否认认证加密,形成认证器密文发送给数据接收者。
(3)数据接收者(data receiver,DR):从收到的认证器密文中计算出原始消息,并能确认消息的来源。
2.2 SM9-DAIBE算法的形式化定义
本节给出新的SM9-DAIBE 算法,该算法由以下四个算法组成:
(1)系统参数生成算法Setup(1λ)。该算法由密钥生成中心负责执行。输入一个安全参数λ,通过运行算法返回系统参数param和系统主私钥ke。密钥生成中心秘密保存系统主私钥ke,公开系统参数param。
(2)用户密钥提取算法Extract(ID)。该算法由用户和密钥生成中心交互执行。用户将自己的身份标识ID发送给密钥生成中心,密钥生成中心对收到的身份标识ID进行合法性验证,验证通过后用系统主私钥计算身份标识ID对应的私钥deID并通过安全信道发送给用户。同时,用户根据系统公开参数计算自己的公钥并公开。
(3)否认认证加密算法DAEnc(M,deS,IDS,IDR)。该算法由数据发送者负责执行。根据消息M、发送者私钥deS、发送者和接收者的身份标识IDS和IDR,数据发送者计算消息M的认证器密文δ后将其发送给数据接收者。
(4)否认认证解密算法DADec(δ,deR,IDR)。该算法由数据接收者负责执行。收到数据发送者发送的认证器密文δ后,数据接收者根据自己的私钥deR和身份IDR,恢复出消息M,同时确认消息是否为数据发送者发送。若是,接收消息M;否则,输出错误符号▲。
2.3 SM9-DAIBE算法的安全模型
(1)SM9-DAIBE算法的保密性
SM9-DAIBE算法的保密性的安全性概念称为抗适应性选择密文攻击的密文不可区分性(ciphertext indistinguishability against adaptive chosen ciphertext attacks,IND-DAIBE-CCA)。下面给出IND-DAIBECCA的游戏定义。
初始化阶段算法B 输入一个安全参数λ,运行系统参数生成算法Setup(1λ),返回系统参数param和系统主私钥ke,其中系统参数param发送给攻击者A,系统主私钥ke秘密保存。
询问阶段1A以如下自适应方式执行多项式有界数量的用户密钥提取查询、否认认证加密查询和否认认证解密查询。
①用户密钥提取查询。当攻击者A要查询标识ID的私钥时,挑战者B 运行用户密钥提取算法Extract(ID)获取对应用户的私钥deID,并将其发送给攻击者A。
②否认认证加密查询。攻击者A选择一个发送者的身份标识IDi、一个接收者的身份标识IDj、一个明文M,并将它们发送给挑战者B。挑战者B 首先运行用户密钥提取算法Extract(ID)获得发送者IDi的私钥,然后运行否认认证加密算法DAEnc(M,deS,IDS,IDR),将计算结果发送给攻击者A。
③否认认证解密查询。攻击者A 提交一个DAEnc 认证器密文δ和一个接收者的身份标识IDj给挑战者B。挑战者B 首先运行用户密钥提取算法Extract(ID)获得接收者IDj的私钥,然后运行否认认证解密算法DADec(δ,deR,IDR),将计算结果发送给攻击者A。
挑战在攻击者A决定询问阶段1 结束时,攻击者A输出两个等长的明文M0、M1,以及之前没有做过用户密钥提取查询的两个标识IDS、IDR一并发送给挑战者B。挑战者B 从0 和1 中随机选择一位记为γ,将δ=DAEnc(Mγ,deS,IDS,IDR)的计算结果发送给攻击者A作为挑战。
询问阶段2攻击者A可以像询问阶段1一样发出更多的多项式有界查询,但是在这个阶段,攻击者A不能对身份标识IDS和IDR进行用户密钥提取查询。同时,攻击者A也不能对挑战δ进行否认认证解密查询。
猜测最终,攻击者A输出一比特γ′作为对γ的猜测。如果γ′=γ,表明游戏获胜。
如果对于任意多项式时间攻击者A,其游戏获胜的优势是可忽略的,即,其中negl(λ)为可忽略函数,则SM9-DAIBE算法满足保密性。
(2)SM9-DAIBE算法的否认认证性
此处借用数字签名中抵抗适应性选择消息攻击的不可伪造性的概念来定义SM9-DAIBE 算法的否认认证性的安全概念。然而,SM9-DAIBE 算法中的安全概念与数字签名算法的安全概念有本质的不同。这是因为在数字签名中,只有具有正确私钥的发送方才有能力生成有效的签名,而在SM9-DAIBE算法中,发送方和接收方都有能力生成有效的SM9-DAIBE 认证器密文。SM9-DAIBE 算法的不可伪造性的安全性概念称为抗适应性选择消息攻击的否认认证性(deniable authentication against adaptive chosen messages attacks,DA-DAIBE-CMA)。下面给出DADAIBE-CMA的游戏定义。
初始化阶段算法B 输入一个安全参数λ,运行系统参数生成算法Setup(1λ),返回系统参数param和系统主私钥ke,其中系统参数param发送给攻击者X,系统主私钥ke秘密保存。
攻击阶段和前面的IND-DAIBE-CCA的游戏定义一致,攻击者X 以自适应方式执行多项式有界数量的用户密钥提取查询、否认认证加密查询和否认认证解密查询。
伪造阶段攻击者X 输出一个DAEnc 认证器δ∗和两个身份标识IDS和IDR。如果同时满足以下三个条件,视为攻击者X 游戏获胜。
①δ∗是一个对于发送方IDS和接收方IDR有效的认证器,也就是说,DADec(δ∗,deR,IDR)的结果不是一个错误符号▲。
②攻击者X 没有对IDS和IDR做过用户密钥提取查询。
③攻击者X 没有对消息M∗和身份标识IDS和IDR做过否认认证加密查询。
这里把攻击者X 的优势定义为它在游戏中获胜的概率。为了实现SM9-DAIBE算法的否认性,在以上条件的第二步需要攻击者X 对IDS和IDR均没有做过用户密钥提取查询,原因是接收者也可以生成一个有效的DAEnc认证器密文。
2.4 SM9-DAIBE算法的构造
SM9-DAIBE算法的具体构造如下:
(1)系统参数生成算法Setup(1λ)。在输入安全参数λ后,该算法执行以下操作:
③密钥生成中心生成系统参数param=(G,Ppub-e,H,hid)并公开,同时秘密保存系统主私钥ke。
(2)用户密钥提取算法Extract(ID)。在输入用户标识ID后,该算法执行以下操作:
①给定用户标识ID,密钥生成中心计算用户的私钥deID=[ke+H(ID)]P2。
②密钥生成中心通过安全信道将用户私钥deID发送给用户。
③用户ID根据系统公开参数计算自己公钥QID=Ppub-e+[H(ID)]P1。
注:本文假定发送者和接收者的公私钥对分别是(QS,deS)和(QR,deR)。
(3)否认认证加密算法DAEnc(M,deS,IDS,IDR)。在输入消息M、发送者私钥deS、发送者和接收者的身份标识IDS和IDR后,该算法执行以下操作:
②利用密钥派生函数KDF,计算K1||K2=KDF(Hv,C1||t||IDR,|M||IDS|+v),其中K1和K2的长度分别为|M||IDS|比特和v比特。
③数据发送者计算C2=K1⊕(M||IDS),C3=Hv(C2||K2)。
④数据发送者将DAEnc认证器密文δ=(C1,C2,C3)发送给数据接收者。
(4)否认认证解密算法DADec(δ,deR,IDR):在输入认证器密文δ、接收者私钥deR、接收者的身份IDR后,该算法执行以下操作:
①数据接收者根据自己的私钥deR计算t′=
②数据接收者利用KDF 计算出K1||K2=KDF(Hv,C1||t′||IDR,|M||IDS|+v)。
③若Hv(C2||K2)=C3,返回M||IDS=K1⊕C2,从而恢复出消息M;否则,返回错误符号▲。
正确性分析:由于C1=[r]QS,QID=Ppub-e+[H(ID)]P1,deID=[ke+H(ID)]P2,有
因此,数据接收者可以计算出正确的中间密钥K1和K2,进而恢复出原始消息M。
3 SM9-DAIBE算法的安全性分析
3.1 否认性
本算法实现了否认性,由于接收者也可以生成有效的DAEnc 认证器密文,而该认证器密文无法与发送者的认证器密文进行区分,原因如下:
(1)在收到发送者发来的DAEnc 认证器密文δ=(C1,C2,C3)后,接收者通过运行否认认证解密算法,获得恢复后的消息M。之后接收者可以执行以下操作:
3.2 保密性
本文所提SM9-DAIBE 算法在随机预言模型下满足抗适应性选择密文攻击的密文不可区分性。
定理1在随机预言模型下,若攻击者A能以优势赢得密文不可区分性游戏(至多进行qH次哈希询问),则存在一个算法B 能利用A 以的优势解决DBDH问题。
证明可以通过2.3 节中定义的密文不可区分性IND-DAIBE-CCA 游戏来证明本文算法的保密性。若存在一个攻击者A可以破解这个算法,则可构造一个算法B 来解决DBDH问题。不妨设算法B 要解决的一个DBDH 实例元组为:Y=(P1,[x]P1,[y]P1,P2,[y]P2,[z]P2,Z)。在下面的游戏中,B 扮演攻击者A的挑战者。
初始化阶段算法B 输入一个安全参数λ,运行系统参数生成算法Setup(1λ),生成系统参数param=(G,Ppub-e,H,hid),其中为双线性配对群,Ppub-e=[ke]P1且ke未知。挑战者将系统参数param发送给A。
询问阶段1A执行多项式有界次数的以下查询,B 对A的查询做如下回答:
(1)哈希查询OH(IDi)。首先,B 维持一个形如(IDi,ni)、初始为空集的二元列表LH。其次,B 选择两个不同的数N1,N2∈{1,2,…,qH}。如果IDi是A的第N1(i=N1)次询问,则B 回答QN1=Ppub-e+[x]P1。如果IDi是A 的第N2(i=N2) 次询问,则B 回答对于一个由A给定的标识IDi(i∈{1,2,…,qH}且i∉{N1,N2}),B 首先检查列表LH是否存在元素(IDi,ni)。
(2)KDF 查询OK(IDi,ti,li)。首先B 建立一个形如(IDi,ti,Ki)、初始为空集的列表LK。当A 询问(IDi,ti,li)的输出结果时,B 首先检查LK中是否存在形如(IDi,ti,Ki)的三元组。
①若存在,当|Ki|≥li时,返回Ki的前li比特。否则,随机选取li-|Ki|长度的比特串K,返回Ki||K给A,同时替换(IDi,ti,Ki)为(IDi,ti,Ki||K)。
②若不存在,则B 询问列表L1(见用户密钥提取查询)中的每个元素对应的哈希列表元素(IDi,dei)。根据dei的取值,B 随机选取长度为li的比特串Ki,返回给A,并将(IDi,ti,Ki)添加至列表LK中。
(3)用户密钥提取查询。首先,B 建立一个形如(IDi,dei)、初始为空集的二元哈希列表L1。其次,B选择一个随机元素r∈。当A询问身份标识IDi的私钥时,B 首先查询列表L1中是否存在元素(IDi,dei),并以如下形式返回对应的dei给A。
①若存在,则B 将dei返回给A。
②若不存在:
如果IDi是第N1或N2(i∈{N1,N2})次询问,则游戏失败终止。
否则,B 首先询问OH(IDi)对应的哈希列表是否包含元素(IDi,ni)。若包含,则B 计算dei=[r+ni]P2,将结果返回给A,并将(IDi,dei)更新至列表L1中。
若不包含,则B 执行哈希查询OH(IDi),选择一个随机数ni∈,将dei=[r+ni]P2的计算结果返回给A,同时更新LH、L1两个列表。
(4)否认认证加密查询。A向B 提交发送者的身份标识IDj、接收者的身份标识IDk和明文M。如果j∉{N1,N2},B 通过查询列表L1获得身份标识IDj对应的私钥,若不存在,则通过用户密钥提取查询和哈希查询OH(IDi)生成用户IDj的公私钥对,接着运行否认认证加密算法,计算δ=DAEnc(M,dej,IDj,IDk)的结果发送给A。如果j∈{N1,N2},游戏失败终止。
(5)否认认证解密查询。A 向B 提交一个DAEnc 认证器δ=(C1,C2,C3) 和接收者的身份标识IDk。如果k∉{N1,N2},B 查询列表L1是否存在标识IDk的私钥dek。若不存在,则通过用户密钥提取查询和哈希查询OH(IDi)生成用户IDk的私钥,运行否认认证解密算法,将恢复出的消息M发送给A。如果k∈{N1,N2},游戏失败终止。
挑战在A决定询问阶段1结束时,A输出两个等长的明文M0、M1以及之前没有做过密钥提取查询的两个身份标识IDS、IDR一并发送给B。如果A在游戏中向B 询问过IDS和IDR的私钥,则B 失败,游戏终止。同时,若IDS和IDR均不是(S,R∉{N1,N2}),则B 仍失败,游戏终止。为了计算DAEnc认证器密文,B 执行以下操作:
(1)B 通过用户密钥提取查询和哈希查询OH(IDi)生成身份标识IDS的私钥。
询问阶段2类似于询问阶段1,A允许继续询问私钥和密文解密等,但A不能对身份标识IDS和IDR做用户密钥提取查询。与此同时,A也不能对挑战δ做否认认证解密查询。
猜测最终A输出一位。如果B 输出0,否则输出1。
用F表示A对挑战身份的猜测不正确,此时模拟会终止。
3.3 否认认证性
本文所提SM9-DAIBE 算法在随机预言模型下满足抗适应性选择消息攻击的否认认证性。
定理2在随机预言模型下,若攻击者X 在一定时间内赢得DA-DAIBE-CMA游戏,则存在一个高效的多项式时间算法解决DBDH问题。
证明此处通过2.3节定义的挑战者B 和攻击者X 之间的DA-DAIBE-CMA 游戏证明本文算法的否认认证性。如果存在一个攻击者X 可以打破这个算法,那么可以使用攻击者X 来构造一个算法B,进而解决DBDH问题。类似定理1中保密性的证明,游戏的过程描述如下:
初始化阶段算法B 输入一个安全参数λ,运行系统参数生成算法Setup(1λ),返回系统参数param=(G,Ppub-e,H,hid),其中为双线性配对群,Ppub-e=[ke]P1且ke未知。X 将系统参数param发送给攻击者X 。
攻击阶段与定理1 证明中询问阶段1 的查询一致,X 执行多项式有界数量的哈希查询、KDF 查询、用户密钥提取查询、否认认证加密查询和否认认证解密查询等。
目前没有公认的解决DBDH困难问题的有效算法,因此实际上不存在这样的攻击者X,证明该算法具有否认认证性。证毕。
4 性能分析
本章从理论分析和实验分析两方面出发,将本文所设计的SM9-DAIBE 算法与文献[5,19,21]中算法进行比较。
4.1 理论分析
表2 比较了4 个算法的参数大小和主要运算时间。符号说明:N表示用户的密文数量,“Exp”表示指数运算,“Pairing”表示双线性对运算。在比较各算法所需的运算操作次数时,忽略了除指数运算和配对运算之外的操作。SM9-DAIBE 与文献[5,19,21]中的算法运算均需基于双线性对运算。不妨假定|G1|=|G2|=|GT|=1 024 bit,|ID|=160 bit,|M|=160 bit以及哈希值|H|=160 bit,因此可计算出文献[19]的通信规模为|ID|+|G1|+|M|+|G2|=2 368 bit,文献[21]的通信规模为|ID|+|G1|+|M|+|G2|+|H|=2 528 bit,文献[5]和本文算法的通信规模为|ID|+|G1|+|M|+|G2|+|GT|=3 392 bit。图2给出了这4个算法通信规模的具体条形图。
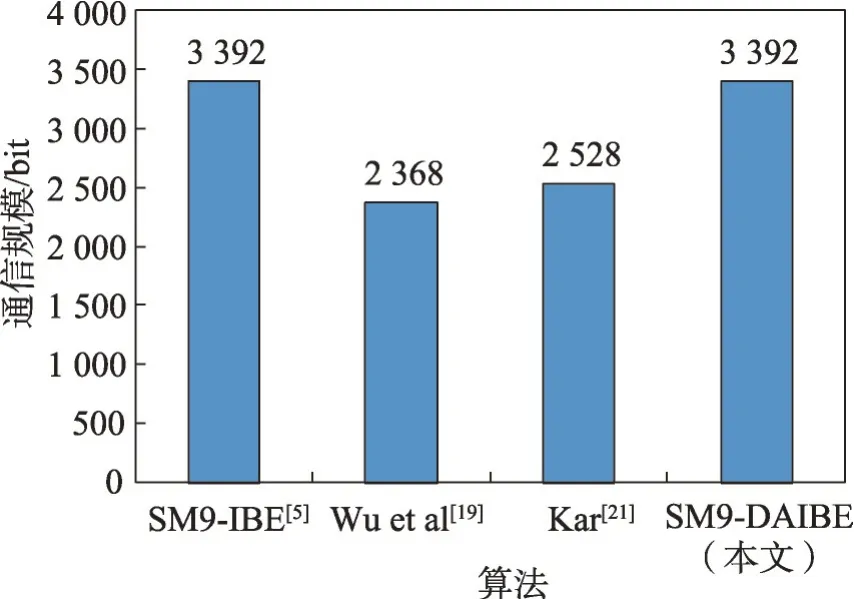
图2 通信规模比较Fig.2 Comparison of communication scale

表2 性能比较Table 2 Performance comparison
通过表2 和图2 的比较可以看到,本文SM9-DAIBE 算法保持了原始SM9-IBE 算法[5]的系统公钥和私钥的选取方式。与文献[19,21]相比,对于用户加密和解密算法,文献[19]共需要4次双线性配对运算,文献[21]共需要3 次双线性配对运算,而本文仅需要2次双线性配对运算。一般来讲,双线性配对运算较其他运算耗时较多。因此,本文算法相比文献[19,21]的算法在用户加密和解密等方面具有一定的优势。并且本文算法采用安全参数小的非对称双线性对,用户的公私钥分别由两个不同的循环群生成,安全强度更高。正因此,本文算法中增加了乘法循环群GT,这使得该算法在通信开销上相较于文献[19,21]中的算法会有所增加。
4.2 实验分析
本节通过仿真实验将本文算法与文献[5,19,21]在发送方计算成本(CS)和接收方计算成本(CR)两方面进行对比。实验环境为荣耀笔记本(3.20 GHz的64 位AMD Ryzen 7 5800H with Radeon Graphics处理器、16 GB内存(RAM)、Windows 10操作系统),使用PBC库[23]中的A型配对实现了4个算法,并获得图3所示的实验结果。A型配对构造在嵌入度为2的曲线y2≡x3+x(modp)上(其中p≡3 mod 4 且为素数)。
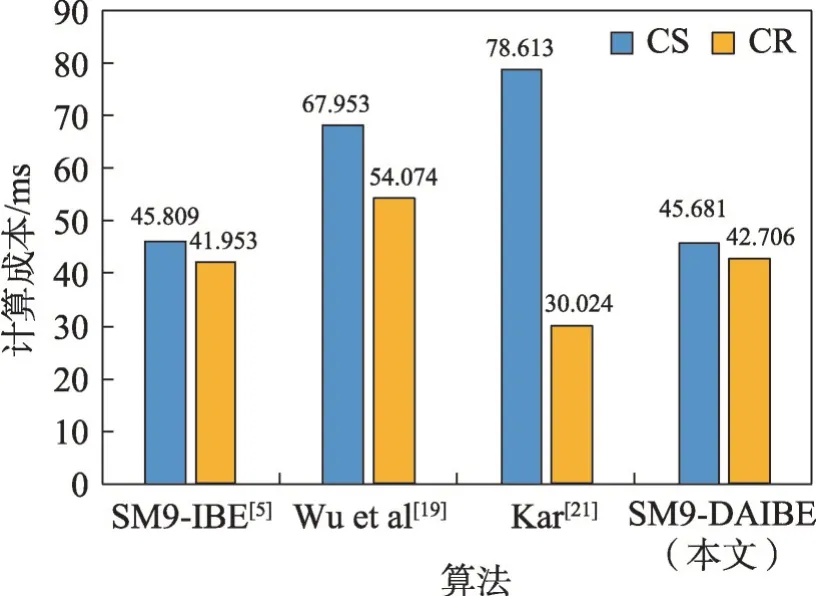
图3 主要计算成本对比Fig.3 Comparison of main calculation cost
从图3 可以看到:对于文献[5],CS 是45.809 ms,CR 是41.953 ms;对于文献[19],CS 是67.953 ms,CR是54.074 ms;对于文献[21],CS 是78.613 ms,CR 是30.024 ms;对于本文算法,CS 是45.681 ms,CR 是42.706 ms。本文算法与原始SM9-IBE算法的发送方和接收方的计算成本相当;相对于文献[19]的算法,发送方和接收方的总计算成本减少了28%;相对于文献[21]的算法,发送方和接收方的总计算成本减少了18%,计算性能更优。
5 结束语
本文将国密SM9 算法和否认认证协议相结合,提出SM9-DAIBE 算法,证明算法同时满足否认性、保密性和否认认证性。结果表明,该算法所具有的否认认证属性,对发送者的身份隐私保护具有很高的实用性。但由于提出的解决方案是基于非对称双线性对,虽然基于非对称双线性对安全强度更高,但是相应也增加了通信开销。在后续工作中,可以考虑进一步减小通信开销。
