多维度偏好建模的动态兴趣点群组推荐算法
2023-10-29孙明阳马玉亮王国仁
孙明阳,马玉亮,袁 野,王国仁
1.东北大学 计算机科学与工程学院,沈阳 110167
2.东北大学 信息科学与工程学院,沈阳 110819
3.北京理工大学 计算机学院,北京 100081
兴趣点推荐任务通常是面向用户个体推荐一组该用户可能感兴趣的地点。随着互联网数据信息的海量化和地理社交网络(geo-social networks,GSNs)的不断发展,人与人之间的联系越来越紧密。以往的用户个体活动也逐渐发展为群组活动,推荐问题的主体也从用户个体向群组进行延伸。兴趣点群组推荐问题也逐渐成为很多学者的研究热门课题之一,且在娱乐、社交媒体、文旅活动[1-3]等领域具有广泛的应用。
兴趣点群组推荐问题是向一组用户推荐他们可能感兴趣的一组地点,例如几个朋友想找一个地点聚会。在现实生活中,群组决策的方式复杂多样,例如听从朋友的意见、听从专业人士的意见、坚持自己的观点等。群成员可能会因为其他成员的决定而对自己的选择产生变化,也可能因其专业性对群组最终决策拥有较大的话语权。现有研究主要致力于将深度学习[4-6]的相关技术应用于群组推荐系统,并取得了良好的效果。
然而,现有的群组推荐模型很大程度上只适合处理无特定相关上下文信息的群组推荐任务。兴趣点推荐问题具有很强的上下文信息相关性。具体而言,兴趣点推荐的上下文信息主要包括时间、地点上下文信息。时间上下文信息表示用户在某一时间段内的偏好,地点上下文信息多数反映用户到达新地方的偏好变化。此外,兴趣点群组推荐通常存在兴趣本地化和活动本地化的现象,其中兴趣本地化是指不同地方的用户兴趣存在很大差别,活动本地化是指用户通常在周边进行活动。然而,现有的兴趣点群组推荐模型的群组聚合策略往往是静态的,无法模拟复杂的动态决策过程。因此本文对地理社交网络中的动态兴趣点群组推荐展开研究,将用户多维度嵌入学习和注意机制相结合,考虑地理社交网络的动态特征,提出基于神经网络结构的动态兴趣点群组推荐模型。
本文的主要贡献如下:
(1)提出了一种新颖的面向地理社交网络的群组推荐模型,该模型基于用户的多维度偏好建模和群组决策的动态过程相结合,实现动态兴趣点群组推荐。
(2)为了刻画地理因素对用户偏好的影响,本文在用户偏好建模阶段进行多维度嵌入学习,即融合群组成员的偏好、兴趣点的空间和时间特性、协同用户的影响,增强用户偏好的表示学习。
(3)利用神经网络结构并以群组成员的增强嵌入表示为核心实现决策过程的动态性,提高兴趣点群组推荐的准确率。
(4)在真实数据集上进行了一系列的实验,结果表明本文提出的模型在推荐命中率等方面优于现有的群组推荐模型,充分验证了本文提出模型的有效性。
1 相关工作
群组推荐方法大致分为两类,基于内存(memorybased)的方法和基于模型(model-based)的方法。基于内存的方法又可细分为基于偏好聚合的方法和基于分数聚合方法。其中基于偏好聚合方法的主要思想就是提取每个成员的偏好信息和群组成员间的关系信息,并将偏好信息整合形成一个伪概要文件,根据概要文件进行推荐。例如文献[7]在推荐电视节目的问题中,通过提取用户的偏好来构建概要文件,然后通过用户概要文件聚合算法,形成一个共同的用户配置文件来反映群体大部分人的偏好信息。基于分数聚合方法的主要思想就是计算群组中每个成员对于候选物品的偏好分数,最后将分数聚合并排列完成推荐。通常包括三种常用策略,即平均策略[8]、最小痛苦策略[9]、最大满意策略[10]。
基于模型的群组推荐方法的主要思想是模拟群组决策过程相结合,设计出能更好反映实际的模型。例如Wang 等人[11]提出了BTF-GR(bidirectional tensor factorization model for group recommendation)模型,在社会群体背景下,考虑用户与群组之间双向的影响关系,即用户偏好和群组决策之间的相互作用;Guo等人[12]将社会影响放在首位来设计组推荐模型,将个性、专业程度、社交网络、用户偏好等因素综合考虑;Yin等人[13]同样以社交影响为核心,并模拟群体其他成员对于某个推荐项的容忍(愿意接受不喜欢的内容)和利他(愿意接受朋友喜欢的内容)因素进行建模。从群组推荐问题的衍生至今,用户偏好不再是单一的因素所决定的,与社交网络、社会影响[6]等相关因素相结合来更好地模拟现实中所做出的决策过程是目前更多人所研究的方向。近些年它们在传统的推荐中得到了广泛的应用。目前很多学者致力于将深度学习的相关技术和方法应用于群组推荐系统。例如He 等人[4]提出了GAME(graphical and attentive multi-view embeddings)群组推荐模型,该模型是基于用户、推荐项与群组之间相互表示、相互影响的思想[5],从多个视图出发,并利用表示学习和神经交互学习两个部分来完成群组对推荐项分数的动态预测过程。Tran 等人[14]提出了MoSAN(medley of sub-attention networks)群组推荐模型,利用次级注意网络中群组成员之间的相互作用来动态分配群组成员的注意力权值完成群组偏好聚合过程。Cao等人[15-16]提出了AGREE(attentive group recommendation)模型,该模型将注意机制首次引入应用于群组推荐领域,根据每个用户的历史数据对每个组成员动态地分配注意力权重,并在预测阶段通过多层神经网络完成推荐。
在兴趣点群组推荐问题中,Zhu等人[17]以兴趣点的距离为中心,充分考虑群组决策时兴趣点的合理性,并采用基于距离的预过滤和基于距离的排名来调整群组满意度。现有的兴趣点[18]推荐方法通过考虑类别、距离等多个方面来建模,以兴趣点为核心,忽略了用户偏好的影响,很少有研究能将GSNs中的特性同用户偏好相结合进行统一建模。并且现有模型方法的聚合策略大多数都是静态的,这些静态的预定义策略在设置群组成员权重过程中缺乏灵活性,不能准确地反映群组成员在群组决策过程中动态的变化过程。因此本文提出了基于多维度偏好建模的动态兴趣点推荐算法,实验表明该算法能够有效地提高推荐的准确率。
2 问题定义
本章介绍论文中所使用的主要符号、兴趣点群组推荐问题中的相关定义。常用符号及其描述如表1所示。

表1 符号描述Table 1 Notation description
定义1(地理社交网络)地理社交网络将传统的社交网络同地点相结合,加入了位置因素,以便在社会结构中的用户可以共享嵌入位置信息。在GSNs中,本文使用Users={u1,u2,…,un}表示用户,用POIs={p1,p2,…,pm}表示兴趣点信息,每个地点由一个二元组(lat,lon)唯一确定且对应现实世界中的某个具体位置。对于GSNs中的每个用户可以随时在GSNs中签到并产生一条签到记录,其中签到记录表示为三元组(ui,pj,time)的形式。
表2 为Foursquare 中部分签到数据示例。其中用户和兴趣点通过UserID和POI唯一确定,每个兴趣点都对应唯一的坐标信息lat、lon,每条用户活动记录对应一条时间戳信息time。
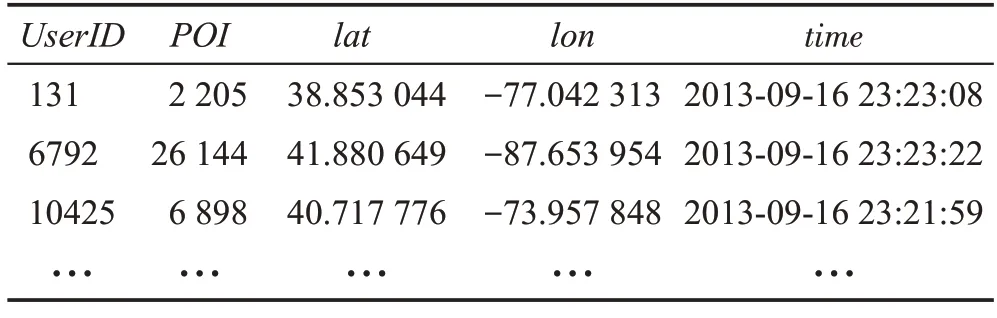
表2 Foursquare中的签到数据示例Table 2 Example of check-in data on Foursquare
定义2(群组-兴趣点感知图)群组-兴趣点感知图如图1 所示,主要由两层网络组成,包括用户层和地点层,将用户偏好与时间特性和空间特性相结合用于群组成员与地点时间的建模阶段。定义为Gg={Vg,Eg},具体规则构建如下:

图1 群组-兴趣点感知图Fig.1 Group-POI awareness graph
(1)顶点集Vg包含群成员顶点和兴趣点顶点;
(2)边集Eg包含在群成员和兴趣点顶点之间,即如果在给定的时间段内群成员访问过该兴趣点,则它们之间存在一条边,并且将边赋予相应的权值。其中权值的大小由群成员访问频次最高的兴趣点与该兴趣点之间距离来决定,计算公式如下:
问题定义在GSNs中,对于任意给定群组g和时间节点time,动态兴趣点群组推荐的目标是学习一个预测函数F(g,time,p|Θ),其中p为某个候选的兴趣点,Θ表示函数F的模型参数。
3 模型概述
本文将模型分为表示学习层、表示聚合层、预测优化层三部分。模型的整体架构图如图2所示,将用户的嵌入信息和地点信息作为模型的输入,群组对于推荐兴趣点的预测分数作为模型的输出。在进行表示学习之前,本文先将用户和兴趣点进行向量表示,将其作为模型中的基本表示单元。本文首先使用one-hot 编码来表示用户u∈Users和兴趣点p∈POIs的所有状态,即。然后使用两个可训练的矩阵E∈Rn×d和F∈Rm×d来将它们转变为同维的嵌入表示向量,即ui∈Rd和pj∈Rd。
3.1 表示学习层
在该部分,本文将用户偏好表示分为三部分:用户嵌入表示Us、用户-兴趣点嵌入表示Up、协同用户嵌入表示Uc。并通过聚合策略最终得到用户的最终嵌入表示。
3.1.1 用户嵌入表示
在该部分本文将用户自身嵌入表示Us作为用户表示向量的一部分,它表示用户的历史偏好信息,考虑的是用户的原始偏好。
3.1.2 用户-兴趣点嵌入表示
在该部分本文充分考虑用户与地点签到关系,从空间影响和时间影响两方面出发对其进行建模。空间影响是分析用户日常活动的一个重要因素。在以往的研究[19]中表明用户的出行签到数据往往与用户中心距离服从幂律分布的特征。根据对用户签到记录分析可以直观地感受到:用户的签到记录往往反映了用户的中心活动范围。用户的签到往往更倾向于签到中心活动范围附近的兴趣点。时间影响同样也扮演着重要的角色,用户在不同时间段的访问地点会有较大的差异性,例如用户在中午更有可能访问的是餐馆而不是酒吧。
基于以上分析,本文首先将一天中的时间分为五部分{T0,T1,T2,T3,T4},分别表示早上8 点—11 点、中午12 点—14 点、下午15 点—18 点、晚上19 点—23点、半夜24点—7点,然后以时间段信息为基准,将群成员活动记录进行筛选和分类,从而完成构建群组-兴趣点感知图。
在模型中,用户地点嵌入表示的形式化表示如式(6)所示:
本文对群组成员在特定时间段内所访问过的兴趣点进行加权求和表示,其中系数α(u,t)表示用户对于兴趣点的偏爱程度,并将地理因素同群组成员的偏好相结合。pt表示兴趣点的嵌入表示。Nl表示群组-兴趣点感知图中兴趣点的索引。
在GSNs中,用户的偏好与兴趣点之间的距离呈负相关,即表现为用户通常会选择距离自己范围即中心距离较近的区域进行活动,即如果用户曾经访问过该地点,且用户中心距离与该地点的距离越近,用户再次访问的可能性越大。反之则越小。因此,本文将群组-兴趣点感知图中权值的倒数作为用户对于兴趣点偏好的权重大小,并使用softmax 函数对权值大小进行归一化处理。
3.1.3 协同用户嵌入表示
协同过滤思想[20-21]在推荐系统中得到了很广泛的应用,其根据物以类聚、人以群分的思想进行推荐,即和自己兴趣相投的喜欢同样的物品。因此在兴趣点群组推荐中,本文将用户的协同用户的偏好作为用户偏好表示的一部分。
首先,本文将与该成员用户在相同时间段且签入超过15 个相同兴趣点的用户看作它的协同用户。通过随机采样8个用户,并将这8个用户的嵌入表示进行连接,然后通过非线性转换得到用户的协同用户表示向量。
其中,Uc1,Uc2,…,Ucx表示协同用户的嵌入表示,W(1)为可训练的权值矩阵,即W(1)∈Rd×d,b(1)为可训练的偏置,即b(1)∈Rd。σ为激活函数。
在该阶段的最后一步就是将用户表示的三部分进行聚合,本文通过将用户、地点、协同用户的嵌入表示向量进行聚合,得到一个用户的最终嵌入表示,它不仅包含用户的偏好信息,还将用户的偏好信息同距离和时间相结合,并利用协同过滤的思想将用户偏好进行扩展,得到了最终的用户向量表示。这里本文采取常用的聚合策略进行聚合。
GraphSage聚合[22]:将用户、地点、协同用户的嵌入表示向量进行连接操作,然后对其进行非线性变换。
其中,Us,Up,Uc分别表示用户、地点、协同用户的嵌入表示,W(2)为可训练的权值矩阵,即W(2)∈R3d×d,b(2)为可训练的偏置,即b(2)∈Rd。σ为激活函数。
3.2 表示聚合层
在上个阶段本文得到用户的最终嵌入表示,即与时间、空间、相似用户相结合的用户偏好建模。在群组偏好聚合阶段,本文旨在最大程度地模拟群组在进行决策过程中的动态过程。群组的嵌入表示通过加权和形式来进行表示,公式如式(11)所示。这个群组嵌入表示可以解释为动态地聚合群组中所有成员的特征表示,可以很容易地与某个兴趣点的嵌入表示进行交互得到最终的预测分数。
本文采用神经网络结构中的注意力网络[23]来动态地决定群组成员的权重变化矩阵。如果群组中的用户去过候选兴趣点,则可以理解为它对于这个兴趣点有一定的了解,它在群组决策过程中的权重会占用较大的比重。在神经网络中,一般通过注意力网络来将该权重量化,并通过归一化函数来将动态的注意力权重量化。如式(13)所示:
其中,W(4)、Wu、Wv为可训练的注意层矩阵,b(3)、b(4)为可训练的偏置,σ为激活函数。对于上述计算出的群组成员的权重系数ω(i,j),本文得到了群组偏好聚合的表示向量。
3.3 预测阶段
到目前为止,本文得到了群组对于某个特定兴趣点和兴趣点的嵌入表示向量。在预测阶段,本文通过将两部分嵌入表示向量乘积运算,对两个嵌入向量之间的相互利用进行建模。该方法已经在文献[24-25]中被证明在神经结构的低层特征交互建模是非常有效的。然后本文通过设置多层感知机来捕获群组与兴趣点之间的非线性特征和高阶相关性,如式(14)所示:
其中,⊗表示两个向量的元素乘积,el为经过L层感知机后的输出向量,W1,W2,…,Wl为可训练的注意层矩阵,b1,b2,…,bl为可训练的偏置。σ为激活函数,本文使用非线性的ReLU 作为激活函数。最后将多层感知机的输出向量el转换为预测分数,如式(15)所示:
3.4 目标函数
本文采取链路预测中常用的成对学习的目标函数来进行训练,大多数的链路预测任务的结果取值为0或1,为了能与链路预测总体结果保持一致,只需将正样本的排名高于负样本即可。本文沿用上述思想,使用Ο表示训练集,三元组(g,p,n)表示群组g曾经访问兴趣点p,但未访问过兴趣点n。即p表示正样本,n表示负样本。因此正样本与负样本的预测分数差值为1,则目标函数如下式所示:
3.5 群组推荐算法
算法1基于多维偏好建模的动态兴趣点群组推荐
本节对基于多维偏好建模动态兴趣点群组推荐算法进行阐述,其过程如算法1所示。具体地,第3~9行为模型的第一阶段,其中包括群组-兴趣点感知图的构造过程、嵌入表示学习的过程,最终得到多维度偏好建模后的用户嵌入表示。第10~13 行为模型的第二阶段,在该阶段利用神经结构中注意力网络动态聚合群组偏好信息,最终得到群组偏好的嵌入表示。第14~16行为模型的第三阶段,其中包括利用多层感知机得到预测分数,并根据目标函数计算梯度,然后进行多轮反向传播更新模型中的参数,直至模型不再收敛,完成训练。
4 实验
4.1 实验设置
在数据集方面,本文使用来自Foursquare 和Gowalla 两个真实地理社交网络的签到数据集来进行实验。其中,Foursquare 数据集包含24 941 个用户,28 593 个兴趣点,1 196 247 次签到;Gowalla 数据集包含5 628 个用户,31 803 个兴趣点,620 686 次签到。签到信息包含用户ID、兴趣点ID、时间戳和坐标信息。这两个数据集的统计信息显示在表3 中。对于兴趣点群组推荐问题,在本文实验中使用文献[17]提出学术模拟中常用的方法来捕获群组的签到信息。具体而言,如果几个用户在1 h内访问同一兴趣点,并且这几个用户相互之间存在社交关系,则这些用户和兴趣点构成一条群组签入信息。
4.2 评价指标
本文采用广泛使用的命中率(hits ratio,HR)和归一化折损累积增益(normalised discounted cumulative gain,NDCG)作为评价指标。命中率强调预测的准确性,是指满足用户的需求的兴趣点在返回的推荐结果中所占的比率。归一化折损累积增益关心找到的这些兴趣点是否放在用户更显眼的位置里,根据测试项出现的位置来进行评估而不仅仅考虑它的出现,即强调顺序性。在实验中,本文考虑HR@K和NDCG@K来表示测试集中所有记录的平均命中率和平均归一化折损累积增益。对应公式为式(17)和式(18),本文将推荐序列k的长度分别设置为5、10、15、20。
4.3 基线方法
本文选取三种算法进行对比,其中包括传统的推荐协同过滤算法和基于注意力机制的群组推荐算法。其中传统的协同过滤算法采用平均策略、最小痛苦策略、最大满意三种不同的聚合策略。本文对四种基线方法进行了综合比较。
CF+AVG[8]:基于用户的协同过滤算法以用户为中心,通过用户与用户的相似性来评估组中每个用户对于不同兴趣点的推荐分数,然后利用平均聚合策略来评估群组推荐的最终分数。
CF+LS[9]:基于用户的协同过滤算法以用户为中心,通过用户与用户的相似性来评估组中每个用户对于不同兴趣点的推荐分数,然后利用最小痛苦聚合策略,着重于群组中每个成员得分最低的兴趣点分数作为群组推荐的最终分数。
CF+MS[10]:基于用户的协同过滤算法以用户为中心,通过用户与用户的相似性来评估组中每个用户对于不同兴趣点的推荐分数,然后利用最大满意聚合策略,着重于群组中每个成员得分最高的兴趣点分数作为群组推荐的最终分数。
AGREE[15-16]:该模型将注意机制首次应用于群组推荐领域,根据每个用户的历史数据对每个组成员动态地分配注意力权重,并在预测阶段通过多层神经网络得到群组对于某个特定兴趣点的预测分数。
4.4 实验结果
实验1(嵌入维度的影响)对于嵌入维度d的取值,本文通过设置不同d的取值并在两个数据集上进行实验,实验结果如图3所示。在实验中d的取值为16、32、64、128、256,并以K=10 为例。当嵌入维度d的取值在128时命中率达到最大值,随后性能便出现下降的趋势。这是因为本文基于对用户偏好的多维度建模,需要较大的嵌入维度编码更多的用户信息,过小的d不能较好地整合用户偏好的相关信息,而过大的d则会出现数据的过拟合现象,导致整体性能下降。
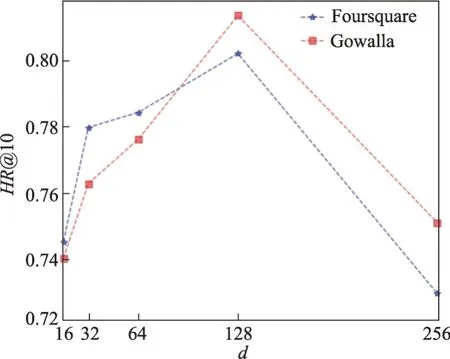
图3 不同嵌入维度对本文模型的影响Fig.3 Effect of different embedding dimensions on proposed model
实验2(命中率分析)本组实验分别在Foursquare、Gowalla两个数据集上对兴趣点的命中率指标进行测试。当嵌入维度d取值128时,通过与对照算法在命中率指标上的结果进行分析,以表明本文提出模型的有效性,实验结果如表4、表5所示。

表4 Foursquare数据集中HR@K 性能对比Table 4 HR@K performance comparison on Foursquare dataset
实验结果表明本文算法取得了最佳的效果,基于分数聚合的算法例如CF+AVG、CF+LS 等在预测兴趣点问题中表现较差,而AGREE算法是基于神经网络的算法,两者的实验结果对比表明AGREE算法的整体性能明显高于传统的方法,证明了预定义的策略已经不能准确地反映群组成员在群组决策过程中动态的变化过程。在与AGREE算法对比过程中,本文算法获得了最佳的效果。尤其是在K取值为5、10 时,HR 指标明显高于对比算法,但是随着K的取值不断增加,本文算法同AGREE算法的命中率相差越来越小。这是由于随着K的增加,算法的容错率也在逐渐增加,对比算法也会在命中率指标上有着不错的表现。
实验3(归一化折损累积增益分析)本组实验分别在Foursquare、Gowalla 两个数据集上对兴趣点的归一化折损累积增益进行测试。当嵌入维度d取值128时,通过与对照算法在NDCG指标上的结果进行分析,以表明本文提出模型的有效性,实验结果如表6、表7所示。
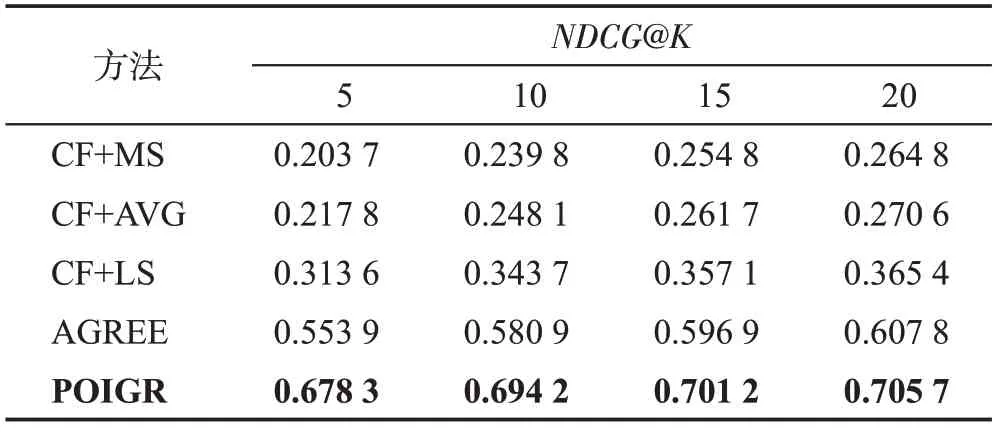
表6 Foursquare数据集中NDCG@K 性能对比Table 6 NDCG@K performance comparison on Foursquare dataset
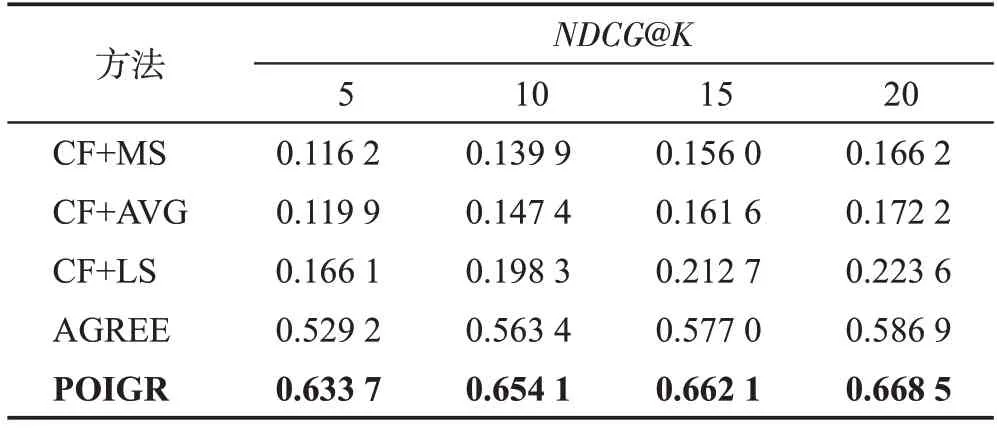
表7 Gowalla数据集中NDCG@K 性能对比Table 7 NDCG@K performance comparison on Gowalla dataset
实验结果表明本文算法在K的所有取值上NDCG 指标均取得了最佳效果,上文中提到随着K的增加,本文算法的命中率与对比算法的结果越来越接近,但NDCG指标仍然明显高于对比算法,即目标兴趣点的预测分数位于预测集的前列。表明本文算法能够更加准确地建模用户和群组偏好,同时也证明了本文算法的有效性。
5 结束语
本文提出了一种解决兴趣点群组推荐问题的新方法,首先本文从用户的偏好表示出发,以GSNs 中的特性为核心进行多维度偏好建模并进行表示学习,增强用户偏好的表示学习。然后利用神经网络结构中的注意机制动态地进行偏好的聚合。最后在两个真实数据集上的实验表明本文算法的整体性能优于现有算法,证明了本文算法的有效性。
在未来的研究中,本文提出了两个可扩展的方向。为了保证推荐的准确性和高质量,对用户偏好建模得相对复杂,导致训练时间较长,因此在未来的研究中可以通过简化用户偏好模型,衡量训练时间和准确率之间的关系,并设计出训练时间与准确率的收益函数,使得推荐的收益得到最大化。本文的研究重点是如何从已有的用户记录中挖掘有效的信息,然而冷启动问题是推荐系统中面临的挑战之一,因此在未来的研究中,如何对没有用户记录或者存在较少用户记录的用户完成推荐是研究的重要方向之一。
