立足素养重思维 减负提质重基础
——2023年安徽省中考数学试卷评析
2023-10-28安徽省芜湖市教育科学研究所邮编241000
安徽省芜湖市教育科学研究所 金 奎 (邮编:241000)
安徽省芜湖市镜湖新城实验学校 章 昀 (邮编:241000)
2023年安徽省中考试卷,助力“双减”政策落地,注重初高衔接,充分体现“稳中求变,传承创新,回归基础,落实素养”的命题指导思想,全面考查抽象能力、运算能力、几何直观、空间概念、推理能力、数据直观、模型观念,重视应用意识和创新意识的培养,突出理性思维及数学在高中选拔中的重要作用.中考数学试卷相比去年难度略微提高,考查学生综合能力更加突出.
1 试卷概况
1.1 试卷特点
2023年安徽省中考数学试卷试题依据《义务教育数学课程标准(2022版)》的内容和要求命题,体现课程标准的评价理念和课程改革的方向.试卷延续“稳中求新,关注数学本质”的特点,发挥“以标施教,教考衔接”指导作用,以“新颖灵活、别具一格”,凸显数学学科的育人价值.
1.2 总体设计
1.2.1 坚持素养立意,凸显育人导向
试题以核心素养为导向,关注通性通法,综合考查“四基”(数学基础知识、基本技能、基本思想和基本活动经验)、“四能”(发展运用数学知识与方法发现、提出、分析和解决问题的能力)与核心素养(会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界).适当提高了探究性和综合性试题比重,创设自然真实情境,助力应用能力考查,凸显育人导向.
1.2.2 遵循课程标准,考查关键能力
试题依据课程标准所规定的课程目标、内容要求、学业要求和学业质量进行命题,各领域内容所占比例与其在课程标准中所占比例大体一致,难易程度大体平衡,保证了命题的科学性.例如试卷23道试题取材广泛,在面向全体学生的基础上,考查关键能力.第9题,第10题,第14题,第22题,第23题为数学水平各异的学生提供了展现自己的舞台.
1.2.3 落实“双减”政策,促进教考衔接
试题具有时代特征,服务于“双减”政策.在反套路、反机械刷题上下功夫,突出强调对基础知识和基本概念的深入理解和灵活掌握,引导课堂教学,促进考教衔接,2023年试题依托教材,高于教材,如试卷第23题是沪科版九上第59页第13题的衍生,第19题是沪科版九上第131页第3题的变式,第21题是沪科版八下第136页第5题的重新加工.
1.2.4 关注数学本质,新颖灵活创新
中考数学试题关注数学本质,灵活创新.如第5题,第9题,第14题,试题的命制关注函数的变量和对应关系,回归函数本质,展现了函数的育人价值.如第23题函数压轴题灵活创新,数形结合和分类讨论,以面积的形式考查二次函数的本质问题.再如试卷最大的亮点之一为选择题的压轴题第10题,考查线段和、面积及周长的最值,本题也可从特殊情况推广到一般情况,回归数学本质问题.
1.3 试卷结构
试卷考点分布较广,“数与代数”46.3%,“图形与几何”40.7%,“统计与概率”13% .试卷重点对数、式、方程、不等式、函数、统计、概率、三角形、三视图、四边形、图形的变换、相似三角形、解直角三角形、圆等知识进行了考查,知识点分布如下.

表1 2023年安徽中考数学试卷知识点分布
2 典例赏析
例1(2023安徽第18题)
观察思考

规律发现
请用含n的式子填空:
(1)第n个图案中“◎”的个数为__________;
规律应用
(3)结合图案中“★”的排列方式及上述规律,求正整数n,使得连续的正整数之和1+2+3+……+n等于第n个图案中“◎”的个数的2倍.
评析本题图形变化规律问题,可以从“形”和“数”两个角度入手,识图、辩图、观察、分析、归纳,列出代数式,从特殊到一般,一般到特殊.此题图形优美、设计巧妙,让学生学会用数学的眼光观察、积极思考、归纳总结得出结论,最后运用用数学语言进行表达,将抽象能力、推理能力与运算能力融为一体.
例2(2023安徽第16题)根据经营情况,公司对某商品在甲、乙两地的销售单价进行了如下调整:甲地上涨10%,乙地降价5元.已知销售单价调整前甲地比乙地少10元,调整后甲地比乙地少1元,求调整前甲、乙两地该商品的销售单价.
评析本题较好地体现数学来源于生活,以学生熟悉的生活题材为背景,引导学生关注社会,发现问题情境中等量关系,考查了学生的阅读能力和逻辑推理能力,能运用数学知识解决实际问题.本题依托教材,回归基础,落实素养.
例3(2023安徽中考22题)在Rt△ABC中,M是斜边AB的中点,将线段MA绕点M旋转至MD位置,点D在直线AB外,连接AD,BD.
(1)如图1,求∠ADB的大小;
(2)已知点D和边AC上的点E满足ME⊥AD,DE∥AB.
获得由中国烹饪协会颁发的“2017年度百家中国好食堂”奖项;被洪山区食品药品监督管理局认证为A级餐饮服务食品安全等级……文华学院在保障校园食品安全方面落在实处,科学管理与人性化服务相结合,俘获了广大师生的味蕾,让人赞不绝口。
(i) 如图2,连接CD,求证:BD=CD;
(ii)如图3,连接BE,若AC=8,BC=6,求tan∠ABE的值.

图1 图2 图3
评析本题为几何压轴题,难度较大,试题以问题串的形式出现,难度层层递进,综合考查学生运用平面几何知识分析问题和解决问题能力,体现了对逻辑推理素养的考查.
本题注重体现基本图形的性质和判定应用,考查学生对数学问题的探究能力,综合性强.以直角三角形斜边中点为旋转中心从图形变化角度进行命题,增加试题的探究性,三个问题分别从角、线段及三角函数值三个方面对进行图形进行定性和定量分析,学生可以利用所学知识从不同角度去思考.
第(1)问求角度可以从旋转后等腰三角形角的性质结合三角形内角和求出,也可以利用圆的定义得到A、C、D、B四点共圆,利用同弧所对圆周角相等得出∠ADB=90°.
第(2)问从定量分析转入定性分析在限定的位置条件下证明线段相等,可以借助于判定四边形MADE的形状为菱形,结合菱形性质,从全等三角形,圆,以及中垂线等不同角度给予解答,增加了试题的探究性和开放性.
第(3)问在第(2)问的基础上,通过添加辅助线构造直角三角形,在特殊的直角三角形中解决问题.
在考查学生核心知识点的同时,题目中以旋转为基础推导出隐藏的等线、等角、四点共圆、中垂线等为该题提供了丰富的想象空间. 近几年安徽中考命题喜欢从“图形的变换”方式入手,结合平时的动手操作,构建基本图形注重寻找图形变化的本质,彰显对“图形的性质”内容涉及的思想方法的领悟和迁移.

图4
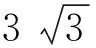

C.△CDE周长的最小值为6
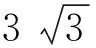
评析本题体现安徽卷一贯特点,试题源于教材、高于教材,体现《课程标准》所倡导“面向全体学生”这一基本理念,又肩负为高中选拔人才的功能.
本题是几何图形的动点最值问题,依旧是教材《最短路径问题》的应用和拓展,但不同的是此题设计四个最小值的计算,增加了试题的难度,但四个答案之间有所关联,解题的难点在于确定动点P的位置,试题以双等边三角形为载体设计问题,有浓厚的数学韵味,考查等边三角形、最短路径、三角形、四边形等知识,很好的将教材中的分散内容整体化,考查学生对知识认知的系统性和学生思维的敏锐性,强化教考衔接.引导教学淡化“题型+技巧”的机械化训练模式,改变传统教学模式,在教学中力求让学生经历数学知识的生成过程,引导学生数学思考,减轻学生过重的学业负担.

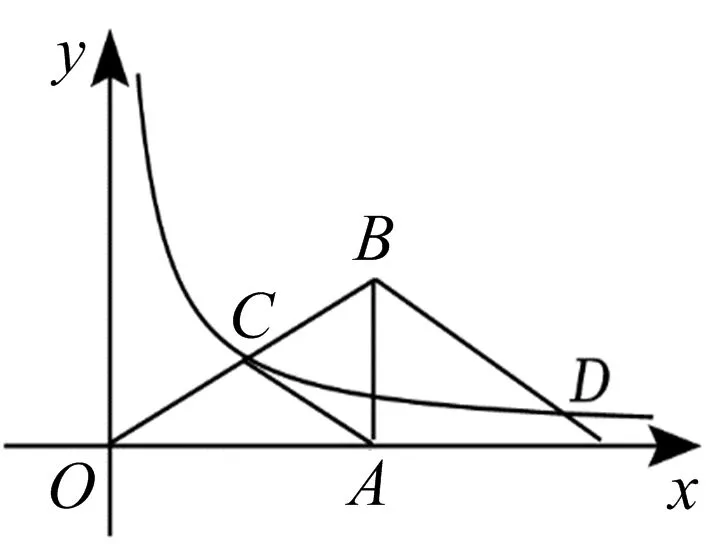
图5
(1)k=______;
(2)D为该反比例函数图象上的一点,若DB∥AC,则OB2-BD2的值为__________.
评析本题问题设置新颖,从两函数题的命题上可以看出,突出了函数的核心内容,深入考查函数的图像和性质以及综合应用,从继承走向发展,在发展中融合创新,渗透了对数学抽象、逻辑推理、数学建模、数学运算等数学学科核心素养的考查.
第(1)小问结合特殊直角三角形性质、中点转化C点坐标和三角形的面积,结合反比例函数k的几何意义可以顺利解答.

3 反思教学
3.1 立足课标,回归教材
课标是国家意志,是编写教材的基础,是中考的依据, 一线教师要熟读课标.中考数学试题大多来自教材,注重基础知识,加强学校集体备课,吃透教材,领会教材的编写意图,创造性地运用教材,对教材课后习题、例题进行深入研究和有效开发.
3.2 落实双减,减负提质
落实“双减”政策,遵循数学学习规律,减少死记硬背和机械刷题,2023年中考题侧重学生能力考查.教师在一线教学中要放弃题海战术,科学布置课后作业,开展数学活动,给予学生获取相关经验的机会,培养学生分析和解决问题能力,重视学生思维能力培养,重视概念教学,让学生理解数学本质,落实双减,减负提质.
3.3 设置真实情境,注重数学实际应用
2023年中考试题情境取材于学生生活中的真实问题,贴近学生实际,具有现实意义,侧重数学知识应用.例如第16题商品销售问题,让学生感受数学的实用性,学会用数学思维思考现实世界;第19题无人机飞行问题,引导学生热爱科学,学会用数学眼光观察现实世界;例如第21题传统节日问题,弘扬中国传统文化,建立文化自信,让学生学会用数学语言表达现实世界.
3.4 聚焦核心素养,转变教学方式
2023年中考试题对学生的数感、符号表达、运算能力进行全面考察,体现基础性、综合性、应用性和创新性的考查要求,聚焦学科核心素养. 在平时的教学中,一线教师以教材题目简单为由,抛弃教材,重用教辅资料,课堂上概念教学一带而过,通过大量刷题来巩固概念,让学生形成定势思维,完全扼杀学生的创新思维,因此,转变教学方式,迫在眉睫.教师要重视课堂教学,引导学生积极主动思考和探索,重视数学思维活动和知识形成,把“发现问题和提出问题”作为根本任务,为学生创造学习机会,加强对学生学习方式的研究,加强体验式学习方式的运用,重视非认知因素的作用.
