日本数学跨学科学习活动的设置与启示——基于对启林馆《面向未来》初中数学教科书的分析

天津市天津师范大学教育学部 张佳琪 张 楠 (邮编:300387)

北京市人民教育出版社课程教材研究所 李 健 (邮编:100081)

1 引言

《义务教育数学课程标准(2022年版)》对“综合与实践”学习领域进行了较大调整,开创性地从课程内容、学业要求、教学提示 3 个方面细化,在内容方面突出问题性、综合性、跨学科性等特点[1],鼓励学生使用数学和其他学科的知识与方法分析和解决问题[2].在此背景下,中小学数学教师需要格外重视跨学科学习活动,服务于新义务教育数学课程改革的落地.

目前,我国初中阶段的数学跨学科教学研究仍处于探究阶段,在提炼与总结自身已有研究成果的同时,借鉴他国成熟的跨学科案例具有重要的实践价值.近年来,我国已有一些研究涉及美国、澳大利亚等西方国家教科书中的跨学科学习活动[3][4],有必要进一步增强对东方国家教科书中的跨学科学习活动设置情况的研究.

2017年,日本文部科学省颁布了新版《初中数学学习指导要领》(简称:《要领》),并于2021年正式实施.《要领》的总体目标强调:通过数学活动培养学生数学思考的资质与能力,即在政治、经济和文化等领域活用知识的能力[5].在《要领》的指导下,日本初中数学教科书重视跨学科活动的设置.以日本启林馆于2021年出版的《面向未来》初中数学教科书(共三册)为例,每册教科书中的“活学活用”栏目均设置了多个跨学科学习活动.

研究以《面向未来》教科书中的跨学科学习活动为研究对象,从活动选择、问题设置、活动方式三个方面展开分析,旨在析出日本教科书中的优质经验,为我国初中阶段数学跨学科学习活动的开发提供启示.

2 跨学科学习活动的活动选择

在《面向未来》教科书的“活学活用”栏目中,共设置22个跨学科学习活动.依据学习活动所跨学科领域的不同,将其划分为8个类别,见表1.

表1 “活学活用”栏目中的跨学科学习活动

2.1 跨地理领域的学习活动

跨地理领域的学习活动是指融合地理和数学学科中的相关知识点所形成的探究活动,其中包括《约定跨国通话时间》《如何确定日最高气温》两个活动.例如在《约定跨国通话时间》活动中,学生需要通过分析经度地图了解东京、伦敦和纽约三个地区之间的时差,进而利用正负数表示时差,最终通过运算帮助三位异国友人约定合适的跨国通话时间.

2.2 跨物理领域的学习活动

数学与物理之间具有天然的密切关联.跨物理领域学习活动需要学生利用物理定律解决数学问题,其中包括《制作长方体容器》《全身镜的奥秘》两个活动.例如在《全身镜的奥秘》活动中,学生需要借助物理学中光的反射定律和折射定律,确定全身镜纵长与被测者身高之间的关系,进而通过建立数学表达式求解全身镜纵长.

2.3 跨体育保健领域的学习活动

跨体育保健领域的学习活动能够体现数学工具在体育保健领域的应用,具体包括《视力表中的Landoit环》《如何合理规划跑道》和《选拔双摇跳运动员》三个活动.例如在《视力表中的Landoit环》活动中,学生需要应用一次函数和反比例函数的知识建立对象之间的关系,深入了解利用Landoit环进行视力检测中的数学原理.

2.4 跨生命安全教育领域的学习活动

跨生命安全教育领域的学习活动是结合数学学科知识有效实施生命安全教育的重要体现形式,具体包括《模拟逃生地图的防灾训练》《调查紧急地震速报的原理》两个活动.以前一活动为例,需要学生结合数学学科中的位置、方向与比例尺等知识使用地图,进而规避危险区域、确定安全路线,完成逃生地图的制作,见图1.

图1 模拟灾害条件的逃生地图

2.5 跨信息技术领域的学习活动

跨信息技术领域的学习活动,要求学生利用简易的信息技术完成数学学习活动,其中包括《通过编程创造图案》《通过编程排列数字》.在这两个活动中,学生需要利用命令、程序等完成图案的变换或数字的排序,既体现出信息技术在数学活动中的应用性,又彰显出在数学活动中应用信息技术的便捷性.

2.6 跨文化与艺术领域的学习活动

跨文化与艺术领域的学习活动,主要是指在数学活动中积极渗透日本和国际上的传统文化、工艺等,涉及旋转烧、明太子、教科书、芬兰工艺品Himmeli、沙包、龟鹤算共六个活动.例如在《明太子的加工流程》这一活动中,其主要流程是基于问题探究促使学生了解明太子(一种利用鳕鱼卵腌制而成的日本传统食物)的原料配比、制造方法、计量方法等,学生不仅能够在真实情境中获得解决实际问题的经验,同时能够加强学生对日本传统饮食文化的了解.

2.7 跨学校与社会领域的学习活动

跨学校与社会领域的学习活动涉及与学生息息相关的学校或社会领域中的问题,包含《调查学生的学校生活》《调查少子高龄化国家》两个活动.例如在《调查少子高龄化国家》活动中,学生需要根据数据分析日本、印度、希腊和秘鲁四国的人口分布情况,计算其基本统计量生成图表并得出结论.在学生掌握数据统计方法的同时,这类活动还有助提高其对于社会热点问题的关注.

2.8 跨经济领域的学习活动

跨经济教育领域的学习活动,可以使学生在数学活动中接受初步的经济常识教育,包括《如何提高饭团销量》《如何订购团扇最省钱》《抽取收益最大的奖品券》三个活动.这类活动要求学生通过合理计算,获得更大收益或节省资金消耗.例如在《如何订购团扇最省钱》这一活动中,学生需要结合团扇加工公司的收费标准,应用方程和图表合理地设计出花费最低的订购方案.

3 跨学科学习活动的问题设置

问题是数学的心脏.高质量的数学问题是学生学习的助推器,具有鲜明的指向性.对于《面向未来》教科书中的跨学科学习活动,其活动问题具有层次鲜明、灵活多样的特征,推动着活动的进程.具体而言,相关活动问题可以归结为基础性问题、开放性问题和模型化问题三类.

3.1 基础性问题

基础性问题主要考查学生对于数学的基本概念、性质、法则、公式等基础知识的掌握情况,在学生深入探究的过程中发挥着基础性作用,在分析的22个跨学科学习活动中,有11个活动中都设置了基础性问题.

例如《如何合理规划跑道》活动中的问题“如何表示第一跑道和第二跑道的长度?”,该问题要求学生根据跑道示意图(图2)观察其图形特征,进而结合圆的周长公式表示跑道的长度,有助于提高学生利用基础知识(圆的周长这一基本公式)解决实际问题的能力.

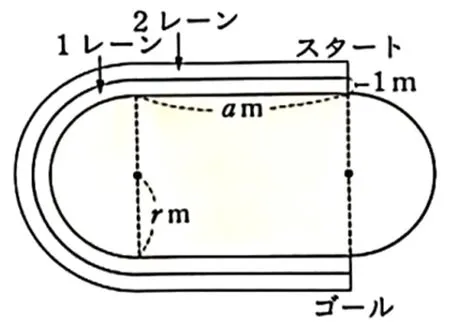
图2 跑道示意图

3.2 开放性问题

讨论跨学科活动的开放性,可以从活动的条件、问题、过程、结果等环节进行分析.[6]《面向未来》教科书中的开放性问题主要体现在问题和结果上的开放性.

问题的开放性主要表现为提供给学生可选择的任务或是由学生自行提出感兴趣的问题.例如《调查少子高龄化国家》学习活动中的问题“除了少子高龄化情况,你是否有其他想要调查的事情?”该问题就需要学生自行提出感兴趣的社会问题开展调查.结果的开放性表现为学生可根据已给条件自行探索得出不同结论,例如《全身镜的奥秘》学习活动中的“关于全身镜的纵向长度,可以得出什么结论”这一问题学生可以从全身镜的物理成像原理、镜长的计算原理等不同的角度进行阐述,得出的结果也就具有多种可能.

3.3 模型化问题

模型化问题要求学生将现实问题数学化,针对现实问题的原型建立数学模型,得出数学结论,其核心思想在于正确建立数学模型,借助模型简化复杂的问题情境.此类问题可以加强数学与生活的联系,有助学生形成数学核心素养.

例如《鹤龟算的原理》学习活动中的问题“鹤和龟的头的总数是35,脚的总数是44,求鹤和龟各有几只.”对于该问题,学生需在明确现实问题的基础上,针对双变量建立二元一次方程模型进行求解.在亲历将现实问题抽象为数学模型的过程中,一方面,有助学生建立数学模型解决实际问题;另一方面,学生能够更好地识别具体情境中的数学本质,体验数学的应用价值.

4 跨学科学习活动的活动方式

教材中的活动方式是指学生进行学习活动过程中所需运用的方法和手段.基于对《面向未来》教科书中的22个跨学科学习活动的分析,可将其预设的活动方式划分为问题探究型、动手实践型和撰写报告型三类.

4.1 问题探究型活动方式

问题探究型活动方式是指将学习活动设计为一系列数学问题,学生需要运用各种数学思想和方法探究分析的一类活动方式.例如《视力表中的Landoit环》这一学习活动中的一系列问题:

问题1如果被测者具有1.5的视力,那么他在多远处可以辨别Landoit环的缝隙?

问题2视力为2.0的被测者的可辨别距离是视力为1.0者的几倍?

问题3当被测者能辨别出多少mm的环缝时,认定为1.5的视力?

问题4视力为2.0的被测者可辨别的缝隙宽度是视力为1.0者的几倍?

该活动结合Landoit环的两个影响因素设置了以上4个问题,对Landoit环的视力检测原理展开探究.问题1和问题2需要学生先研判出被测者距离与视力构成一次函数关系,将实际问题转化为函数问题;问题3和问题4需要学生观察Landoit环的结构(图3),归纳环的大小与其缝隙间的表达式,进而分析出环的缝隙与视力之间的反比关系,转化为函数问题得以解决.在学生明晰Landoit环检测原理的过程中,有助提高其利用数形结合、转化等思想解决问题的能力,有助于促进学生数学思维的发展.

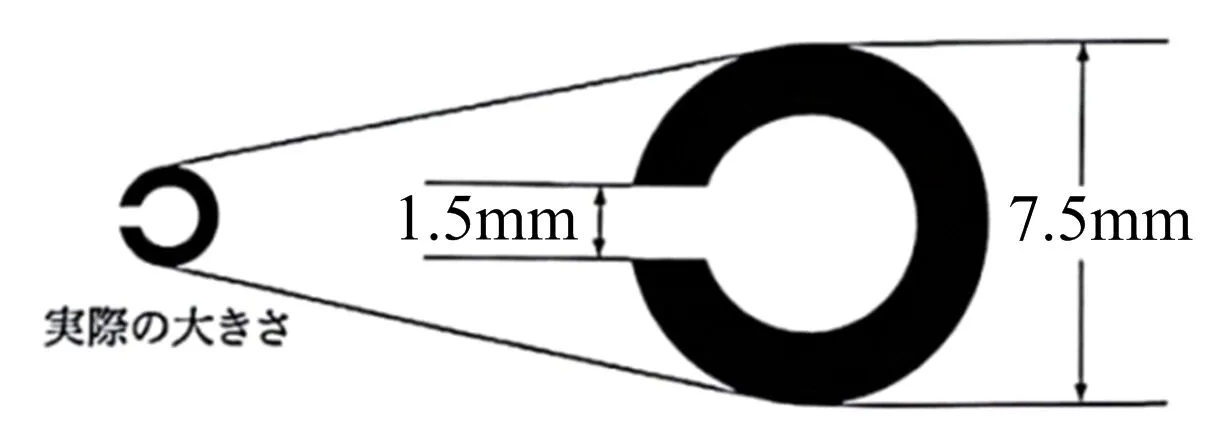
图3 Landoit环结构图

4.2 动手实践型活动方式

动手实践型活动方式要求学生动手操作完成活动,其中包括动手制作和信息技术的应用.例如在《芬兰工艺品Himmeli》学习活动中,学生需要以吸管为材料制作结构相仿的Himmeli(图4),在每个正多面体的制作过程中,都需要学生明确零件的数量和拼接的方式,有助于进一步了解正多面体的基本特征,从而提升学生对于空间几何体的认识水平.此类活动方式是数学理论知识与实践操作相结合的重要体现,学生在动手实践的过程中加深了对正多面体相关知识的理解,又可以利用数学知识更好地指导实践.

4.3 撰写报告型活动方式

撰写报告型活动方式要求学生按照既定的研究报告的构成要素(表2),根据活动主题开展自主调查,再将调查或探究的过程以文字、图表和公式等形式整理成研究报告.

表2 调查研究报告的构成要素

如表2所示,“调查动机”决定着研究报告的整体方向;“调查方法”是总结活动中所应用的知识和方法的过程,在研究报告中起着关键性的作用;“调查结果”是将实际调查的数据及内容归纳成结论,具有总结性的意义;“思考与感悟”是学生完成调查研究后进行的反思与回顾,有助于提升其元认知水平;“参考资料”则是提高报告的科学性和合理性的有效依据.通过撰写研究报告,学生可以初步体会科学研究的严谨性与规范性,有助于培养学生的科学态度和理性精神.

5 启示

通过分析日本教科书中跨学科数学学习活动的活动选择、问题设置和活动方式三个方面的设置经验,为我国设置高质量数学跨学科学习活动提出三点启示.

5.1 拓展多元化数学跨学科学习领域,发展学生学习数学的积极情感

在多次国际教育测评中,我国学生在数学学习兴趣方面始终处于较低水平,长此以往不利于学生未来的发展.影响学生数学情感的重要因素是对数学价值的认识[4],让学生更加全面地认识数学的价值,将有助于突破学生数学情感低下的困境.《面向未来》教科书中的跨学科学习活动涉及8个跨学科学习领域,体现出学科领域多元化的特征.其中,除了地理、物理等数理类学科外,还包含文化与艺术、学校与社会等人文类学科,为学生提供更全面、更多样的学科视角,从而激发学生的学习热情.例如《如何确定日最高气温》这一活动,学生需要通过分析直方图、数据分布等获得气温的最值与变化趋势,能够体会到数学的应用价值,启发学生以多视角分析不同学科间的密切联系;而在《普及沙包的制作方法》活动中,学生可以通过问题的探究了解日本传统沙包的原材料和制作流程,拉近了学生与传统手工艺品之间的距离,有助加强传统文化的熏陶.因此,在设计数学跨学科学习活动时尽可能联结多种学科领域,让学生多角度、全面性地认识数学,发展学生学习数学的积极情感.

5.2 突破知识联结的跨学科融合,促进综合实践能力的生根

在我国新一轮的课程改革中,强调了学生要在综合与实践领域的课程中发展能力与素养,能够运用数学学科和其他学科的基础知识和基本技能,经历发现、提出、分析和解决问题的全过程[1].将不同学科领域的知识关联起来,可以帮助学生从不同角度分析与思考问题,综合运用知识与方法解决实际问题.《面向未来》教科书在知识联结方面就具有良好的示范作用,其跨学科学习活动要求学生联结跨学科知识的内容,拓展分析问题的思路,体会应用多元学科知识解决问题的必要性与有效性.例如在《约定跨国通话时间》活动中,利用识别经度地图引导学生确定不同国家之间的时差,将地理知识与数学知识融合共生.学生在活用知识解决问题的过程中,有助于发展综合实践能力,而跨学科知识的联结为综合实践能力的发展提供了资源沃土,使其深深扎根、动态生长.

5.3 发挥三类活动方式间的优势互补,实现数学思维的“可视化”

数学思维是数学知识与能力的内化,隐藏于学生自身的思维深处,很难外化为“可见”的层面,长此以往不利于教师全面了解学生数学思维的发展现状.因此,如何聚焦学生的思维过程从而实现思维的“可视化”显得尤为重要.《面向未来》教科书设置了问题探究、动手实践和撰写报告三大活动方式促进学生数学思维的表达.问题探究类活动方式主要以多层次、多梯度的问题串激活学生的思维,问题由易到难、层层递进,引导学生突破思维障碍、凸显思维路径;撰写报告是学生的数学活动思维“可视化”的主要方式,学生需要将头脑中的思维过程外化为语言撰写在研究报告中.动手实践类活动方式是将学生的数学思维“物化”的一种活动方式,在动手实践的过程中学生可以借助可视、可感的材料,将头脑中的思维展现出来,用操作撬启学生思维发展的杠杆.三大活动方式在促进学生数学思维“可视化”的过程中发挥了各自的优势,促使学生的思维过程充分外显,有助于学生数学思维的发展.