2023年新高考2卷第21题的解法探究与溯源
2023-10-28安徽省阜阳市阜南县第一中学卢瑞雪邮编236300
安徽省阜阳市阜南县第一中学 水 涛 黄 豹 卢瑞雪 (邮编:236300)
1 试题呈现
2023年新高考Ⅱ卷第21题为:

(1)求C的方程;
(2)记C的左、右顶点分别为A1、A2,过点(-4,0)的直线与C的左支交于M、N两点,M在第二象限,直线MA1与NA2交于点P.证明:P在定直线上.
从问题的内容看,第(1)问主要考查了双曲线的方程及简单的几何性质;如图1所示,第(2)问考查了直线与双曲线的位置关系.从问题的表述看,问题情境经典,题干简洁明了.解题入口较多,但计算繁琐,对学生的逻辑推理、数学运算、数学建模等核心素养提出较高的要求.

图1
2 解法探究
思路一直线的方向向量的变化导致了M、N的变化,可以从直线的角度出发.
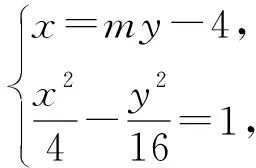

评注解法1和2从直线MN出发,通过设直线→联立方程→韦达定理→解点P坐标解决问题.难点集中在两个方面,一是通过观察图象,确定P点在与x轴垂直的直线上;二是如何解决“非对称”化简问题.解法1寻找y1y2、y1+y2之间的线性关系,解法2利用两根和消去y2,将分子分母化成m与y1表示的式子,得出最终结果.对学生运算求解能力要求较高.
思路二从点P的变化出发.





思路三通过思路一和思路二的探索,发现第(2)问的本质之一是求直线MA1与NA2的斜率比值为定值,进而求解交点P的横坐标为定值.又A1、A2为顶点,可以利用双曲线的“第三定义”和双曲线的方程进行化简.
解法5
①
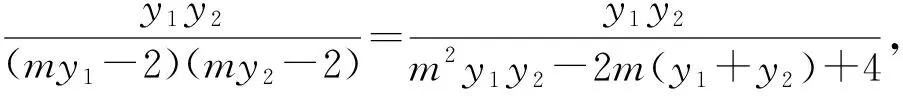
②


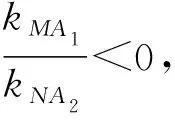
评注解法5先探索发现过定点的弦的端点与顶点连线斜率积为定值,与双曲线的“第三定义”结合,得出直线MA1与NA2的斜率的比值为定值;解法6将斜率比值平方后,利用椭圆的方程消去y1、y2,再利用韦达定理得出结果.解法5和6的本质是利用椭圆的方程进行消元,相对直线消元而言学生平时用得较少,比较陌生,对学生的消元技巧要求较高.
思路三从M、N点的变化出发.
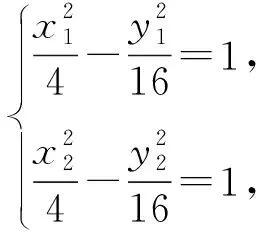

后同解法1.
解法8由解法7知,x1y2-x2y1=4(y1-y2),又(x1y2-x2y1)(x1y2+x2y1)
所以x1y2+x2y1=-y1-y2,与x1y2-x2y1=4(y1-y2),
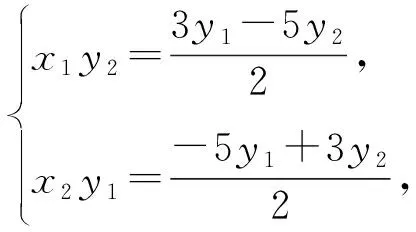
评注解法7通过三点共线建立M、N点坐标与横截距之间的关系,再进行整体代换消元;解法8在解法7的基础上构造对偶式,解出x1y2、x2y1,再带入斜率比值进行消元,得出结论.解法7和8方法巧妙,设点后利用椭圆的方程进行化简,技巧性较强.
思路四考虑到直线变化时,线段长度的比值也在变化,从线段的长度比值出发.
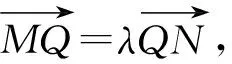
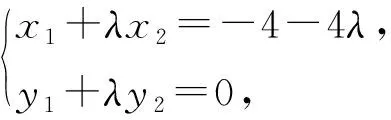
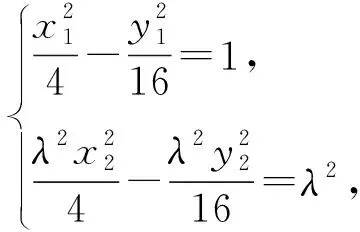
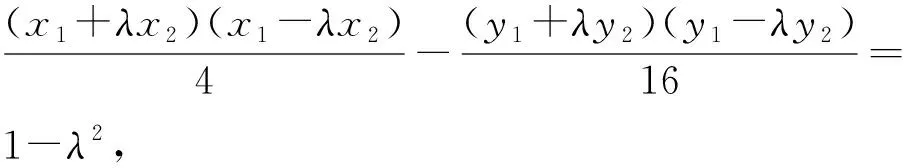

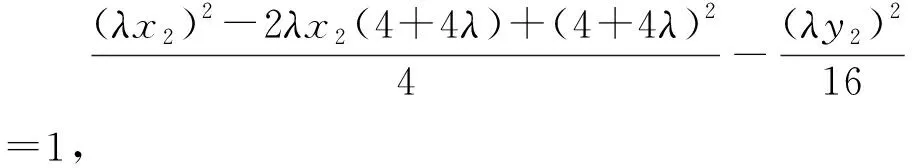

评注解法9和解法10用线段的比值表示直线的变化,利用向量表示这个比值,解法9利用定比点差法,解法10利用“算两次”的思想解出x1和λx2,代入计算得到直线MA1与NA2的斜率的比值为定值;本质上都是利用线段的比值表示点的坐标,解决问题的大方向依然是消元.从这个角度来说,设直线的参数方程也是可以尝试的方法,因为新教材中已将其删去,在此不做讨论.
3 命题溯源
在上文中,笔者利用十种方法解题,殊途同归.那么高考命题人是如何命制本题的呢?王文彬在文[1]中提到,“极点与极线是圆锥曲线的基本特征,因此在高考试题中必然会有所反映,自然也会成为高考试题的命题背景”.本题的命题背景应该也是圆锥曲线的极点与极线.如图2所示,

图2

与本题命题背景类似的还有2020年高考全国乙卷数学理科第20题,2010年全国高考江苏省理科第18题等等,不一而足.
4 结语
任子朝、赵轩在文[2]中指出 “高考数学科提出5项关键能力:逻辑思维能力、运算求解能力、空间想象能力、数学建模能力和创新能力”,本题旨在考查学生的前4项具有鲜明数学学科特点的数学能力,具有较好的甄别功能的试题,也是日常教学中必备的教学资源.对本题的进行解法拓展、命题背景溯源,有利于教师把握高考命题的方向,提升对《普通高中数学课程标准》及《中国高考评价体系》的理解,有助于教师提高解题教学的效率.
