一道平面向量高考题的解法赏析及命题研究
2023-10-28浙江省湖州市南浔高级中学刘太杰刘定勇邮编313009
浙江省湖州市南浔高级中学 刘太杰 刘定勇 (邮编:313009)
平面向量一直是近年来高考全国卷的必考内容,在试卷中常以选择题或填空题的形式出现,属容易题或中档题,纵观近几年的高考全国卷,考查内容从原来的简单概念和基本运算,逐步发展为与三角、解析几何、不等式等整合的综合问题,难度上有增加的趋势,尤其是当出题者从几何背景出发命制试题时,解题方法就显得灵活多变,难度不容小觑.
1 试题呈现


本题以平面向量在圆中的应用为载体,考查向量数量积的最值问题;考查了平面向量的数量积、坐标运算、基底表示、向量投影等基本知识的综合运用;体现了代数问题几何化、数形结合、函数与方程等数学思想. 通过解决问题,有助于学生认识数学内容之间的内在联系,体验数学发现与创造过程,有助于发展学生的数学运算、直观想象和逻辑推理等核心素养.
2 解法赏析
数学家波利亚曾说:“一个有责任心的教师,与其穷于应付繁琐的教学内容和大量的题目,还不如选择一个有意义但又不太复杂的题目去帮助学生深入挖掘题目的各个侧面,在指导学生解题的过程中,提高他们的才智与推理能力.”[1]
视角1代数视角
解法1(数量积的定义)
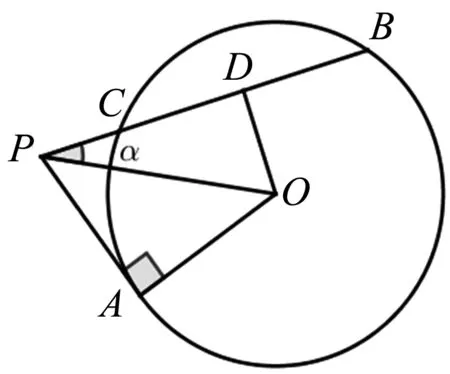
图1
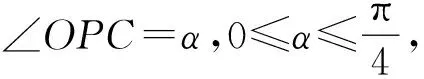

图2
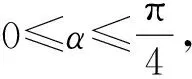

评注解法1主要基于代数视角,从数量积的定义出发考虑问题,思路虽直接自然但过程略显繁琐,具有较大的运算量,对三角函数的化简与求解有较高的能力要求.
解法2(坐标法 + 圆的参数方程)
如图3所示,以圆心O为坐标原点建立平面直角坐标系,

图3


评注解法2主要基于代数视角,从向量的坐标运算出发,通过建系引入坐标,辅以圆的参数方程,将数量积问题转化为三角函数最值问题,与解法1有类似之处.
解法3(基底法)

图4


下面的求解同解法1,故略去.
评注解法3主要基于代数视角,考虑到平面向量的基本定理,借助基底将两个向量分解转化,与解法1、解法2类似,将数量积最值问题转化为三角函数的最值问题来处理.
视角2几何视角
解法4(投影法)


图5


评注解法4主要基于几何视角,透过现象看到了命题者的本质意图,通过前面的解法探究找到了点D的轨迹(隐圆),充分利用数量积的几何意义,将数量积问题转化为向量的投影长度问题,抓住了命题者的出题意图,极大地简化了运算量,轻松快速的得出结论.
视角3数形结合视角
解法5(线性规划)


图6
评注解法5主要基于数形结合视角,通过前面的解法探究找到了点D的轨迹(隐圆),通过数量积的坐标运算将所求问题转化为线性规划问题,形象而直观的解决了问题.
解法6(解三角形)


图7
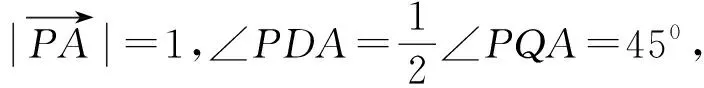
(*)

可以考虑采取三角换元、齐次化、坐标变换等方法求解,下面给出坐标变换的求解方法.
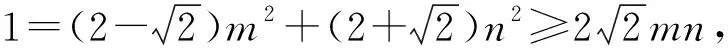

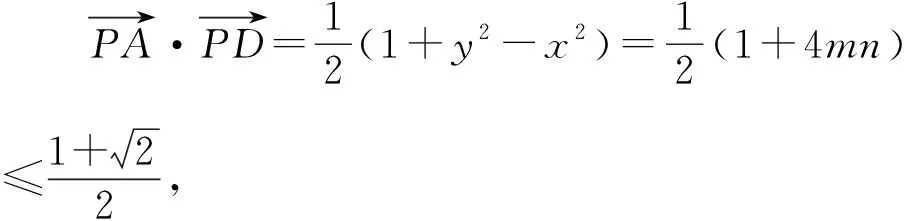
评注解法6在解法5的基础上思维发散,探究了平面向量与解三角形知识的内在联系,最后可以采取三角换元、齐次化、坐标变换等方法将数量积的最大值求解出来,充分展示了向量在代数与几何的沟通中发挥的重要作用.
3 命题研究
通过对真题的溯源,探寻出题人的命题思路与灵感来源,洞悉高考的考查方向;通过对真题的认真分析与深度探究,从条件、结论、形式等方面进行适当的变式、拓展、引申,以期达到对此类问题的彻底消化理解.

A.(-2,6) B.(-6,2)
C.(-2,4) D.(-4,6)
答案:A.
简评不难发现,2023年全国高考乙卷(理)第12题与2020年新高考I卷(山东卷)第7题的命题手法如出一辙,所不同的只是命题载体(圆与正六边形)不同罢了.



答案:(0,1).
简评通过真题变式1、真题变式2,强化学生对投影法的深刻理解与认识,从而达到优化解题的教学目标.


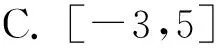
答案:C.
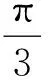


答案:A.
简评通过引申拓展1、引申拓展2,拓广学生的解题视野,提升解题方法与技能(极化恒等式、圆的向量式等),发展数学核心素养.
4 教学启示
平面向量问题一直是每年模拟、高考、竞赛等考试中的热点与重点问题之一,其借助平面几何的背景,创新性、新颖性皆很强,且变化多端,常考常新,同时也是数学知识交汇与融合的理想场所之一,是考试中能力齐全、思维各异、方法多样的一个主战场. 破解平面向量问题,主要是抓住平面向量与平面几何的图形特征,借助基底思维、坐标思维、解三角形思维等方式切入,结合平面向量的相关运算,得以研究相关的几何元素之间的关系问题.
数学家波利亚曾说过:“掌握数学就意味着善于解题,解题就像采蘑菇一样,当我们发现一个蘑菇时,它的周围可能有一个蘑菇圈.”[1]解题是数学教师教学活动的基本形式与主要内容,解题教学是数学课中必不可少的一部分,通过解题教学,教师能发现学生在学习中存在的问题,来优化自己的教学;另一方面,学生通过解题,锻炼了自己的数学思维,巩固与掌握了必备知识,提高了数学学科核心素养与关键能力.
