空气炸锅改进结构仿真及实验研究

2023-10-28陈权明随晶侠郑志伟

家电科技 2023年4期

陈权明随晶侠郑志伟

佛山市顺德区美的洗涤电器制造有限公司广东佛山 528311

0 引言

煎炸是中国最常见的传统烹饪方式之一，煎炸食品口感外酥里嫩，深受大众喜爱，但其含油量较高，且制作过程会产生大量油烟，对人体健康有害，故亟需一个更健康的烹饪方式来替代。近年来国内兴起的空气炸锅产品就是一种替代选择，其采用高温气体在密闭的炸锅内高速回旋对食物进行加热[1-3]，使用少量食用油或者不用油即可煎炸美食。

空气炸锅通常是顶部加热，通过吹风将热风吹至整个腔体。容易让食物受热不均匀，烤的时候必须勤翻面，与空气炸锅“懒人神器”这一称号有所背离，“不翻面”成为各大品牌进行产品升级的主要方向之一[4]。针对免翻技术，目前技术研究发展趋势主要是在空气炸锅空载的情况下进行立体流场均匀性改进。例如结合CFD数值模拟空气炸锅内流体情况，揭示空气炸锅内部的流场运动规律与旋涡结构的产生和发展过程[5]。通过双内胆独立风道及底部扰流结构把上发热管的部分热量导流到腔体底部，对食材下表面进行对流加热，从而达到上、下面同时受热的效果。但在实际使用过程中，由于炸网沾上油污后比较难清洗，用户通常会在炸网和食材之间铺一层锡纸或一次性油纸来达到易清洁的目的，但这种方式会影响底部热风的加热效果，使得食材上、下面的烹饪效果变差，用户仍然需要在烹饪过程中人为翻动食材以改善上、下面的受热均匀性，增加用户烹饪的复杂度。故现有的技术研究未能真正解决用户复杂场景下的翻面问题。

本文旨在通过在空气炸锅的腔体底部增加下发热源，增强底部的传热能力，从而实现在无需人为翻面的情况下，达到食材上、下面受热均匀性良好的效果。首先，对传统型式的发热管进行计算流体力学（Computational Fluid Dynamics，CFD）仿真模拟；然后，基于仿真的温场分布，对发热管形态进行改进设计；最后，对最优的设计方案进行烹饪效果的实验验证。

1 研究对象及控制方程

1.1 研究对象模型处理及基本假设

随着计算机能力的发展，计算流体力学（Computational Fluid Dynamics，CFD）被越来越广泛地应用于各个领域，例如空气炸锅对流换热、烤箱热场模拟设计等[6-9]。本研究采用CFD方法对空气炸锅腔体底部温场进行模拟分析，可以直观看到腔体底部温度分布情况，可对底部发热管的结构形态改进设计提供参考和借鉴，减少金属发热管打样试错次数，缩短设计周期，降低研发成本。

本文主要研究通过在空气炸锅的腔体底部增加下发热管，来提升腔体底部的热均匀性，如图1 a) 空气炸锅示意图所示，核心结构包括以下几个部分：门体、不锈钢锅体、上下不锈钢发热管、腔体及热风组件部分，本研究仅进行底部发热管单因子对温场的影响研究，未考虑流场耦合因素，故为减少网格数量提升仿真效率，可以把顶部发热管及热风组件直接去除以简化结构模型。如图1 b) 简化模型所示，其中锅内及腔体区域设置为流体域，锅体及下发热管设置为固体域。实际过程中其内部存在复杂化的传热过程，例如高温气体对食材的传热过程、高温气体与固体壁面传热过程，固体壁面与保温棉传热过程，保温棉与外部空气传热过程，以及固体壁面、上发热管对食材热传导和热辐射等过程。考虑到文章的研究重点，本文主要针对腔体底部温度均匀性改进进行模拟计算，故进行以下说明及假设：

图1 模型简化处理

（1）固体壁面仅作为壁面，在计算过程中无任何物理特性变化；

（2）模型去除保温棉，通过实测锅底与仿真的温度偏差来调节设置腔体壁面导热系数；

（3）不考虑食材实际烹饪中相变换热过程。

1.2 CFD基本控制方案

在数值模拟中，对于对流换热可以运用动量守恒定律、质量守恒定律以及能量守恒定律进行描述。然后借助数学方程对具体的定律进行表述，生成相应的动量方程、连续性方程以及相应的能量方程[10-11]。

（1）动量守恒方程

给定物体边界的流动概况，其微分表达式为：

（2）连续性方程

连续性方程也被称为质量守恒方程，表述为特定环境下，单位时间内产生的流体微元质量流入和流出趋于恒定。其表达式为：

（3）能量守恒方程

对流换热过程中发生热量的传递与交换，根据温度变化获取能量守恒方程，其表达式为：

上述表达式中，ρ为单位时间密闭空间的密度；t为单位时间密闭空间的具体时间；为速度矢量；p为特定环境中相应的流体微体压力；τxx、τyx、τzx为粘性应力；Fx、Fy、Fz为微元体所受的体积力在三个坐标轴方向的投影；k为导热系数；cp为比热容；T为温度；ST为内热源。使用CFD对空气炸锅温场计算到达稳态时进行分析，故上述方程中∂t=0。

2 网格划分及计算模型

2.1 空气炸锅网格划分

采用Meshing对计算域进行网格划分，如图2 a) 空气炸锅计算域中的整体网格剖视图所示，由于存在腔体的薄壁以及下发热管的曲面，故需通过proximity and curvature进行定义。如图2 b) 腔体及下发热管局部放大图中所示，当腔体网格最小尺寸为0.6 mm，薄壁狭缝层数为1，下发热管曲率控制36°，渐变率为1.2时，能满足对腔体及下发热管固体域进行局部加密处理，提高仿真精度，同时尽可能减少计算量，缩短仿真时长。

图2 空气炸锅计算域网格图

2.2 计算模型确认

综合考虑腔体内传热机理、计算精度和效率等各方面因素，选择k-ε模型。空气炸锅运行时，相应的壁温和浮升力会受空气温度影响，在此基础上需要选择enhanced wall treatment和full buoyancy effects完成相关的模拟分析。辐射换热的模型包括P-1模型、Rosseland模型、DTRM模型以及DO模型等等。由于DO模型适用范围广，计算量适中，故选取DO模型进行本次研究的数值模拟；边界条件的设置如表2所示。

表2 边界条件的设置

3 网格无关性与仿真分析

3.1 网格无关性验证

网格无关性验证结果如表3所示。对网格划分应用了五种方案，网格数量分别是226万网格、303万网格、491万网格、573万网格和735万网格。参考腔体整体平均温度分析得知，当网格数量为226万时，腔体整体平均温度为135.6℃；当网格数量为303万时，平均温度为141.6℃，前两种方案温度偏差为6℃，偏差较大。随着网格数量的提升，较303万网格方案温度偏差皆≤1.1℃，腔体温度逐渐趋于一个稳定值，说明温度不再随网格数量的增加而发生大的偏差，网格满足无关性要求。综合考虑计算精度和计算量，最终确定进行数值模拟的最佳网格数量为303万。

表3 网格无关性验证

3.2 仿真精度确认

图3所示为仿真与实测腔体9点温度对比图，通过采用HIOKI日置LR8450数据采集仪实测采集锅底9点温度，并将CFD结果与实验测量结果进行比较，结果表明：CFD结果与实验结果基本吻合，误差小于5%。在实际产品中由于空气炸锅保温棉填充密度以及包裹松紧偏差等因素，会导致数值模拟结果与实际测试结果存在一定的偏差，故该模型精度符合要求。

图3 仿真与实测腔体9点温度对比图

3.3 传统方案问题分析

图4a) 所示为传统型式发热管方案的腔体温度分布云图，图4 b)为传统型式的蚊香型发热管，发热管均匀盘旋。如图4 a) 腔体温度云图所示，把该类型发热管直接作为下发热管，由于腔体四周与外界环境进行热交换，腔体四周与发热管外围温差较大，导致发热管外围散热速度要比发热管中心散热速度要快，所以出现中心温度比两侧高现象。而发热管靠门一侧由于保温棉无法完全包裹，导致靠门一侧散热较快，腔体前部比后部温度低。仿真的锅底9点温度最大温差为69.5℃，腔体底部温度均匀性较差，故需减少中心区域及加大靠门一侧的发热管密度来进行改进下发热管结构形态。

图4 传统型式发热管方案温度分布图

3.4 仿真改进

通过传统型式发热管仿真分析得知，需减少中心区域及增加靠门一侧的发热管密度，故提出了三种发热管结构形态，下发热管改进方案结构图如图5所示。

图5 下发热管改进方案结构图

图6～图8为三种改进方案的腔体底部及下发热管温度分布云图，降低中心区域及增加靠门一侧的发热管密度有利于改善腔体底部温度均匀性。其中方案1和方案2腔体底部温度靠门一侧仍然出现温度偏低情况，方案1最大温差为43.9℃，方案2最大温差为33.7℃。改进方案3的最大温差为27.8℃，较传统方案69.5℃的均匀性改善提升60%，具体数值如表4所示。

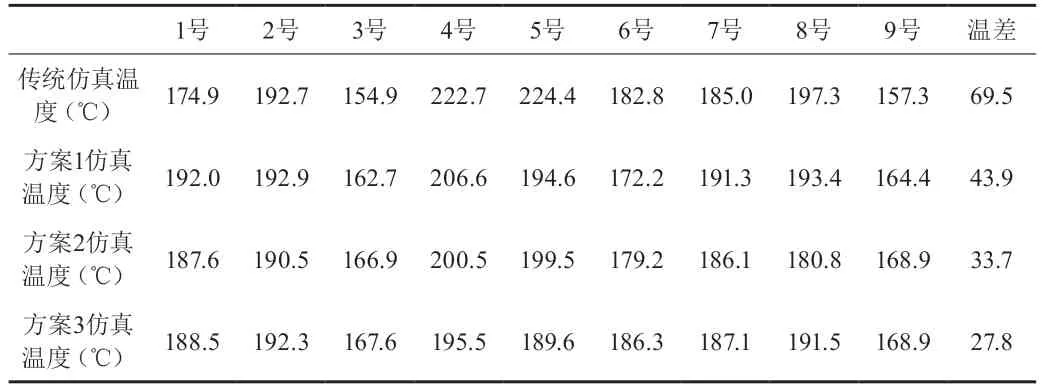
表4 传统型式方案与改进方案腔体底部温度

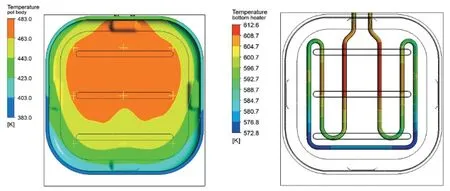
图6 改进方案1：腔体底部及下发热管温度分布图

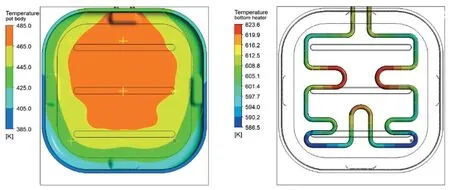
图7 改进方案2：腔体底部及下发热管温度分布图

图8 改进方案3：腔体底部及下发热管温度分布图

4 实验验证

4.1 腔体底部均匀性改进实验验证

表5给出了改进前、后腔体底部温度的实测数值，经过上述方案3改进，原腔体中心位置5的温度由225.7℃下降至196.1℃，锅底9点的最大温度差由57.3℃下降至27.5℃，腔体底部温度均匀改善提升了52%，与数值模拟结果符合性较好。

表5 改进前、后腔体底部温度的实测数值

由于蛋饼液能较好地与锅体贴合，且烹饪结束后可直观通过蛋饼底部上色情况来判断空气炸锅腔体底部的加热均匀性。故以煎蛋饼对比实验验证改进效果：使用打蛋器把鸡蛋液50 g搅拌均匀后，加入100 g清水继续搅拌均匀，最后加入过筛后的100 g中筋面粉搅拌成无颗粒蛋饼液状态。锅底中心控温230℃，预热完成后把蛋饼液倒入锅体中，加热15 min，记录蛋饼底部上色情况。

图9所示为煎蛋饼实测对比图，传统型式发热管的蛋饼中心已经出现焦糊色，而蛋饼四周上色较浅。经过方案3下发热管形态改进，蛋饼底部上色均匀性有明显改善。与上述仿真及温度实测分析结果符合性较好。

图9 煎蛋饼实测对比图

4.2 上下管功率匹配

图10所示为上、下管功率匹配图，通过分别调节上下管的功率大小，使得实测腔体底部与炉心温度偏差≤5℃，拟合上下管功率关系公式，避免腔体底部温度过低或过高而导致煎炸食物底面不上色或上色过深。上下管功率数值拟合关系式如下：

图10 上、下管功率匹配图

式中，y为下发热管功率，x为上发热管功率。该公式拟合度R2=0.9967，拟合度较好。

4.3 烹饪效果对比

在某厨房App的空气炸锅常用高频前十菜谱调研得知，其中干锅鸡翅占比39%位居第一，故通过以空气炸鸡翅来对比百元级普通款、千元级高端款以及改进方案的空气炸烹饪效果，对比两款不同价位段的空气炸锅均为单上发热管加风机组合。

炸鸡翅对比实验：按10 g生抽、2 g老抽、4 g耗油、4 g料酒、3 g白糖及6 g玉米油配比成腌料，把清洗好的6个鸡翅放入腌料腌制1小时。在空气炸锅腔内放置一次性油纸，并把6个鸡翅均匀排布在油纸上，在鸡翅中心内部插入一根热电偶检测温度，空气炸锅设置200℃，检测所有鸡翅热电偶温度到达95℃后停止实验，记录鸡翅上、下表面上色情况。

如图11所示，从实验结果得知，图11 a) 普通款空气炸锅与图11 b)高端款空气炸锅在使用一次性油纸后，鸡翅的背面比顶面上色浅，需要用户中途翻面。图11 c) 改进方案在增加底部热源后，即使用户使用油纸，鸡翅底面依然能够上色，达到上空气炸、下煎的免翻面效果。