一种电力通信网络重要节点识别模型
2023-10-28王炳焱
王炳焱
(广东电力通信科技有限公司,广州 510700)
0 引言
当前智能电网[1-3]技术持续进步,电力系统要求电力通信网络[4]具备越来越强的安全性、抗攻击性、抗脆弱性。作为电网中重要一环,电力通信网络主要根据业务类型定义的服务级别进行分类。节点是网络的重要组成部分,故障节点会影响许多网络服务,甚至中断一些网络服务。从电力通信网络的情况来看,节点故障会中断水平高的电力通信网络服务,或者造成无法接受的电力通信网络延迟问题,这种延迟或者中断,会极大影响电网系统(例如状态监测系统与生产控制系统)的状况[5-6]。所以,确需对关键节点进行识别与保护,以减少网络的风险或者脆弱性。
目前,大量学者对电力通信网络进行了研究。文献[7]基于5G网络进行电力通信网分布式测量系统设计。该系统以网络层、传输层、应用层三方面若干个指标为测量目标,通过探针采集各项数据,综合判断电力通信网运营状态。然而系统未考虑电力通信网络中重要节点的重要性度量。文献[8]提出了一种基于最小路径选择度的电力通信网络路由优化策略。该模型将基于图形卷积网络的链路带宽占用率预测模型的预测结果与三角模算子相结合得到路径选择度,作为电力业务传输路径选择的依据,实现了电力通信网链路资源的动态分配。文献[9]基于PageRank算法设计电力通信网络路由优化方法。该方法通过构建通信网络拓扑结构,获取通信网络特征,基于PageRank算法识别关键节点,调整通信网络的负载策略,设置通信路由目标函数,优化约束条件,使信息资源最大化利用。文献[10]提出一种电力通信网络海量告警信息降噪收敛方法。通过电力系统通信网络的设备状态以及报文接收状态告警之间的关系,建立报文接收状态告警模型。文献[11]以IMS技术体系结构为基础,构建基于IMS技术的电力通信网络跨域融合技术架构。利用该技术架构的接入层连接不同跨域网络终端后经过网关控制协议转换后,实现不同电力通信业务跨域IP入网;电力通信业务进过传输层的Go接口、NGN分组核心网络以及媒体网关、多媒体资源管理器传输到会话控制层内的媒体网关控制功能内并连接出口网关控制功能。上述文献只考虑了节点对从物理拓扑导出的一些指标的影响,如最小路径、最佳路由等。在电力通信网络中,如果物理拓扑中具有高临界度的节点不承载重要流量,而是承载大量常见流量,那么该节点就不是非常重要节点,并且当该节点发生故障时,对电网的影响不会很大。因此,有必要对电力通信网络中的节点重要性进行综合评估。
为提高电力通信网络重要节点识别准确率,本文提出了一种多层节点重要性识别模型,电力通信网络涵盖传输层、物理拓扑层与服务层在内的3个逻辑层,从而综合比较各层节点重要性度量指标。
1 节点重要性
本研究定义了3个网络逻辑层:物理拓扑层、传输层和服务层,并通过不同的方法综合计算电力通信网络三层中节点的重要性度量。不同的层次代表电力通信网络[10-13]的不同视角。本文研究物理拓扑层的过程中,采取图论法对电力通信网络所具备的节点重要性进行分析。将网络[14-15]抽象成一个连通图,由边与节点共同构成,并计算节点介数、度等指标表征节点在长期网络运行中的平均重要性。对传输层而言,能够立足通信网络的性能对节点本身的重要性进行分析,主要分析节点承载相关流量的服务。具有较大流量的节点出现故障的情况下,要通过服务再次进行路由,由其他节点共享这些流量。但是,只能处理有限的流量,增加节点负载的情况下,传输性能反而会降低,例如延迟或分组丢失率。因此,流量大的节点会极大影响通信网络本身的传输性能,进而使节点具备更高的重要性。服务层立足电力通信网络的相关功能,对节点本身的重要性进行了分析。服务本身的重要性,能够表现服务中断影响电网运行的状况。服务重要性和单位流量之间没有必然的关系。具有高重要性的服务通常需要小单位流量。当一个节点发生故障时,其承载着大的服务重要性和较小的流量,对通信网络的性能影响很小,对电网的运行影响很大。
总之,3个网络逻辑层从3个维度对节点的重要价值进行评估:通信网络性能的影响长期平均重要性与节点影响电网运行的状况。
1.1 物理拓扑层
令物理拓扑层表示为G={V,E},其中V={vi},i=1,2,…,N,N为节点的数量,V为节点集,E为边集。电力通信网络中节点在物理拓扑层中的重要性由全局拓扑性质(GTP,global topological properties)与局部拓扑性质(LTP,local topological properties)组成。将LTP中节点i的重要性[16-17]定义为LTP(i):
(1)
(2)
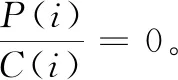
位于网络边缘的边缘节点和位于子网之间的边界节点之间存在显著差异,因为边缘节点的故障对网络的连接几乎没有影响,但边界节点的故障破坏了子网之间的连接,并将网络拆分为几个部分。因此,本研究引入全局拓扑重要性GPT来区分边缘节点和边界节点:
(3)
式中,BC和BC(i)分别是节点介数向量与节点i的节点介数。网络整体中任何节点间经由节点i的最短路径的具体数量决定了BC(i)。两个不同的子网络之间的最短路径需要通过边界节点,这导致了节点介数较大。所以,采取节点介数,能够对边界节点与边缘节点进行区分。
综合式(1)~式(3),节点i在物理拓扑层中的重要性定义为TP(i):
TP(i)=wlLTP(i)+wgGTP(i)
(4)
式中,wl和wg分别为局部和全局拓扑重要性的权重,且有wl+wg=1。具有较高LTP(i)的节点i的故障将主要影响局部区域的连通性,而具有较高GTP(i)的节点i的故障将主要增加网络的平均最短路径长度。本研究中选取LTP(i)和GTP(i)具有相同的重要性,即wl=wg=0.5。
1.2 传输层
电力通信网络传输层主要研究指标是流量分布。一个承载更多流量的节点将产生更大的成本消耗,因此该节点可能至关重要。令BF(i)表示节点i携带的流量。流量包括3个部分:生成、接收和重传。B表示服务请求矩阵,该矩阵是一个三维矩阵,矩阵元素为b(s,d,h),其中s表示源节点,d表示目的地节点,h表示服务类型。b(s,d,h)表征节点s到节点d之间请求的h型服务的数量。令Path(s,d)为节点s和节点d之间的路径。BF(i)定义如下:
(5)
式中,H为服务类型的总数;F(h)为第h类服务的单位带宽。节点承载的流量越多,重要性就越高。
1.3 服务层
电力通信网络中不同类型的服务之间存在显著差异,服务重要性决定了电网能否安全稳定运行。然而,这些服务[18]通常需要较小的带宽。相反,一些服务重要性较低的服务需要的带宽却比较大。稳定系统的服务与安全区中的广域矢量测量、继电保护,具有很高的服务重要性,但带宽要求很小。相反,安全区域的视频监控、视频会议等服务的服务重要性较低,但带宽需求较大。因此,流量较小的节点也可能是关键节点,因为节点上承载的服务很重要。
服务层中的节点i的重要性定义为BI(i):
(6)
式中:I(h)为第h类服务的重要性值。节点i携带的服务重要性值越大,BI(i)就越高。
2 多层节点重要性识别模型
为有效识别电力通信网络中关键节点,本研究提出了一个多层节点重要性识别模型来整合多层节点的重要性,从而搜素综合重要程度最高的关键节点。在多层节点重要性识别模型中,首先计算在单层中关键节点的相关节点的隶属度,其次,求出不同层的可信度与基本测度。最后,对节点本身的临界度进行综合测算。
假设电力通信网络中有N个节点,包括3个逻辑层(物理拓扑层、传输层和服务层)。Ik(i)为节点i在第k层中的重要性,其中k∈[1,3],i∈[1,N]。Ik(i)越高,第k层中的关键节点i越多,因此节点i的隶属度也就越高。将第k层中节点i的隶属度[19-20]定义为mki,则有:
(7)
当计算单层节点关键性度量的隶属度之后,引入了不同层的基本测度可信度反映该层的可信程度。令εk表示第k层的基本测度可信度,εk满足如下公式:
(8)
式中,n为电力通信网络中逻辑层的数量。
在电力通信网络中,服务重要性是最直接地衡量服务中断影响电网状况的指标。所以,加入不同服务之间的重要性存在相当大的差异,则服务层为第一考虑因素。但是,假如电力通信网络的服务重要性具备相似或者相同的情况,要把握节点上能够承载的相应流量,所以传输层为次要考虑因素。而且,假如网络服务有着相似的带宽与重要性,也就是说服务间不存在差异,那么物理拓扑层是最后才需要考虑的因素。为综合考虑三层逻辑层的重要性,本文提出了自适应的基本度量可信度指标:
(9)
ε1+ε2+ε3=1
(10)
式中,ηmin和ηmax分别为服务层的最小和最大重要性值;ωmin和ωmax分别为网络层的最小和最高带宽。如果ηmax远大于ηmin,则ε1就会非常接近数值1,也就是说采取服务层的度量对节点临界度进行确认,是值得充分肯定的。反过来,假如ηmax高度接近ηmin,那么ε1就会非常接近数值0,也就是说,采取服务层对节点本身的临界度进行确认,缺乏较强的不可信性,所以其他层的度量会凸显较强的可信性。在ε1非常接近数值0的情况下,假如ωmax与ωmin的差距较大,即ε2体现出很大的数值,意味着传输层具有非常可信的度量值,能够对节点本身的临界度进行描述。反过来,如果ωmax接近ωmin,意味着相关节点的临界度取最终决于物理拓扑层中的度量值。
在多层节点重要性识别模型中,所有逻辑层中节点的度量均涵盖两个组成部分:首先是选定层中全部节点能够度量的相应几何平均值,第二部分是度量的可信度,即选定层的基本可信度和未选定层的基础度量不可置信度的乘积。对于任意的第x个逻辑层(x∈[1,n],n为电力通信网络中逻辑层的总数),节点i的度量值定义如下:
(11)
式中,mΦi为节点i的度量值;Φ为选择的逻辑层。与之类似,第二部分度量的可信度定义如下:
(12)
式中,Ψ为未选择的逻辑层。
综合式(11)和式(12),电力通信网络中节点i的度量可计算如下:
zΦ(i)=mΦi×CΦ
(13)
式中,zΦ(i)为电力通信网络中节点i的度量。当电力通信网络中包含n个逻辑层时,有2n-1种选择方式。令Z(i)表示的节点i的临界度,即定义为Φ中所有zΦ(i)的和。为计算Z(i),本研究引入二进制序列θ,θk∈{0,1},k∈[1,n]。如果θk=1,在集合Φ中选择第k层;否则,θk=0表示第k层为未选择层。综上,Z(i)可计算如下:
(14)
式中,εk为第k层的基本度量可信度;[θ]为序列θ中1的个数。Z(i)越大,关键节点就越多。
3 仿真与分析
可以这样定义电力通信网络的脆弱性:网络出现弱点(出现障碍或者遭受攻击)的情况下可以继续服务的一种能力。网络中的漏洞来自网络系统的不同领域,如网络的物理拓扑、硬件、软件等。为了验证所提多层节点重要性识别模型的有效性,本节选择不同的识别算法以得到各个节点本身的临界度。按照这些节点的不同等级,将排名靠前的那些节点移除,对重要节点影响网络脆弱性的情况进行测试。网络脆弱性本身的影响越显著,意味着节点的重要性程度也就越高。
3.1 仿真环境与指标选取
仿真时使用MATLAB R2018a作为运行环境。电力通信网络的所有物理拓扑结构由Gephi 0.9.1生成。仿真时设置了五类服务,服务重要性向量分别设置为0.98,0.83,0.553,0.33,0.15。同时,与之相应的带宽分别为0.03,0.08,0.02,0.52,0.14。考虑到不同类别的服务具有不同的重要性和单位流量,网络中传输的服务将不断变化。仿真时随机生成服务矩阵B,并约束服务的总数。为了简化实验过程,将电力通信网络中的边权重全部设置为1。
实验时使用网络效率、剩余网络的服务重要性、节点传输的剩余流量3个指标来验证节点排名的合理性,并执行网络脆弱性度量。各指标分别定义如下:
(15)
式中,NE(G)为网络效率指标,用于表征物理拓扑层的弱点;dij为节点i和节点j之间的最短距离;N为电力通信网络中的节点数量。
受到攻击或故障后剩余网络的服务脆弱性度量定义如下:
(16)
式中,G′为受到攻击或故障后的剩余网络结构;BI(j)为由节点j承载的服务重要性;SLV(G′)为在移除关键节点之后由网络中的节点承载的剩余服务脆弱性度量。
同理,受到攻击或故障后剩余网络的传输流量脆弱性度量定义如下:
(17)
式中,TLV(G′)为在移除关键节点之后由网络中的节点承载的剩余传输流量脆弱性度量;BF(j)为节点j传输的流量。
3.2 实验过程
实验过程中,使用最短路径作为服务传输的路由算法。为简化实验过程,假定被删除节点携带的服务不会被重新路由,即服务的丢失只包括被删除节点的流量和服务重要性,不影响其他节点的流量或服务重要性。
假定对物理拓扑、服务重要性和流量的攻击方法分别表示为攻击物理拓扑(APT,attacking physical topology)、攻击服务重要性(ASI,attacking services importance)和攻击服务流量(AST,attacking services importance)。在本研究中,选择APT、ASI、AST作为攻击算法验证不同逻辑层中节点重要性。
在移除节点之前,物理逻辑层、传输层和服务层的初始指标值均为1,表明网络中节点的服务重要性、流量与效率没有遭受影响。移除相关节点后,各指标开始变化。一个层中的指标下降得越快,表明该层中的节点重要性排名就越合理。移除全部节点的情况下,各个逻辑层的相应指标值都是0。
3.3 结果与分析
为了证实多层节点重要性识别模型的合理性,本节分析了不同模型对网络脆弱性的影响,对比模型包括:APT、ASI、AST、逼近理想解排序法(TOPSIS,technique for order preference by similarity to ideal solution)。
本研究仿真时采用的电力通信网络拓扑结构示意图如图1所示。其中节点1模拟省级调度中心,节点13模拟区域调度中心,节点14代表220 kV变电站,其余节点代表500 kV变电站。根据节点的重要性度量计算,电力通信网络中节点的重要性度量如表1所示。
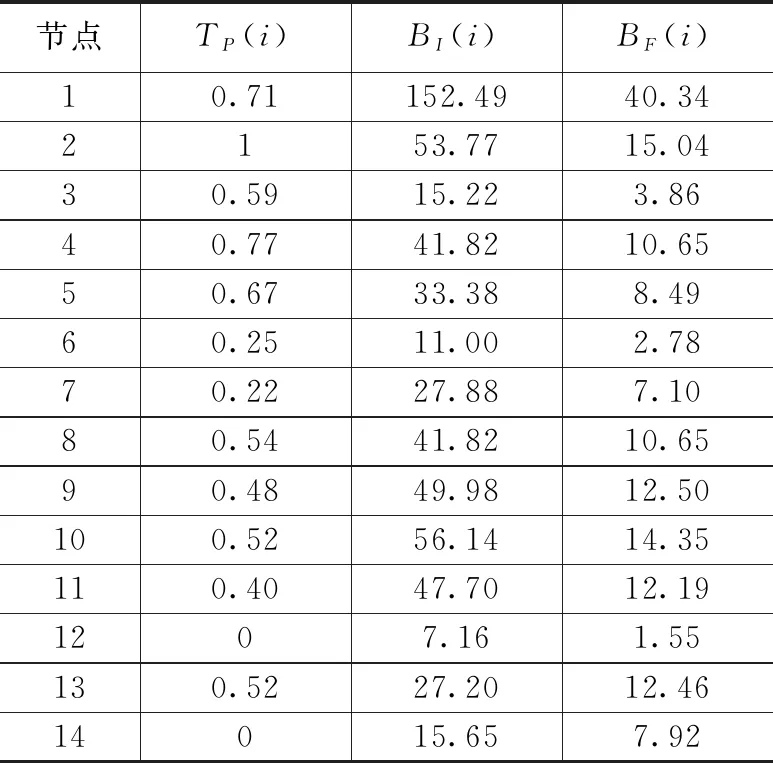
表1 电力通信网络中节点的重要性度量
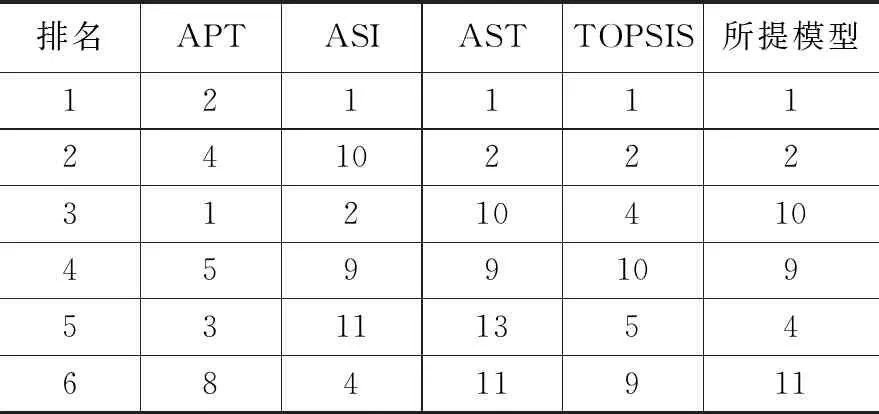
表2 不同算法节点排名
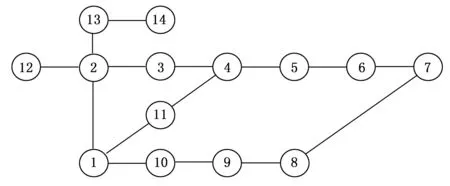
图1 电力通信网络拓扑结构示意图
电力通信网络中,节点1被当作省级调度中心,应该和全部节点(不包括节点14)形成业务连接。而且,节点13对节点14进行调度。省级调度中心、区域调度中心和500 kV变电站间存在着多种类型的服务,主要是对服务进行调度和管理。变电站间的相关继电保护等只能提供数量较少、类型单一的生产控制服务,但包含最重要的服务。通过服务重要性矩阵I和单位流量矩阵F,可以得到基本度量可信度,即ε1=0.571 3,ε2=0.264 8和ε3=0.163 9,分别对应于服务层、物理拓扑层和传输层。
表2为不同算法在关键节点前6(TOP-6)排名。从表2可以看出,通过所提多层节点重要性识别模型的排名主要取决于服务层,传输和物理拓扑层对排名的影响并不大。从物理拓扑重要性方面来看,节点4只紧随节点2,排在第二位。节点4除承载服务以外,也是目的地节点或者源节点,节点4只传输少量服务,这降低了节点4的关键性。同时,节点4和8承载着数量相同的服务类别和服务数量,因为物理拓扑层中各个节点有着不同的重要性,节点8本身的排名并不高。TOPSIS重点关注数据间的相应距离,如此一来节点5比节点9的排名更高。但是,关键节点的排名应该取决于服务层。与节点5相比,节点9在服务和物理拓扑层上更有优势。因此,对应于TOPSIS的关键节点排名并不符合电力通信网络的真实状况。节点10并不具备很重要的物理拓扑,且该节点在物理拓扑层中排名第八。但省调度中心和几个500 kV变电站之间的服务通过节点10,增加了节点10的重要性。
对于案例电力通信网络,将最关键的节点识别出来并不难,也就是节点1。只借助物理拓扑开展节点分析的情况下,节点2最重要,但不符合实际情况。原因在于,在物理拓扑中节点1本身没有处在最重要的位置,然而就能够承载的服务而言,节点1极大地区别于其他节点。节点1本身的故障会急剧降低服务层与传输层的脆弱性。只采取单层对节点关键性进行分析,局限性也是显而易见的。
为了更形象地展示出删除节点影响不同层自身的脆弱性的情况,文章按照顺序,将对应于不同算法的节点排名中的TOP节点观察所有层的脆弱性。不同模型删除节点的脆弱性曲线如图2所示。从图2(a)中可以看出,当同时删除多个节点时,所提多层节点重要性识别模型产生的曲线可以接近服务级别的最优曲线,即ASI曲线。在图2(b)中,所提多层节点重要性识别模型对传输层的脆弱性有很大影响。在图2(c)中,删除[3,5]节点时,TOPSIS略优于所提多层节点重要性识别模型。然而,通过以上定性分析,可以得出结论,在这次仿真活动中,借助TOPSIS方面的关键节点排名,与电力通信网络的真实状况不相符。从给定的服务分布来看,ASI和AST之间的差异在图2(a)和(b)中并不明显,即因为服务的分布使节点同时承载大量流量和服务的重要性。
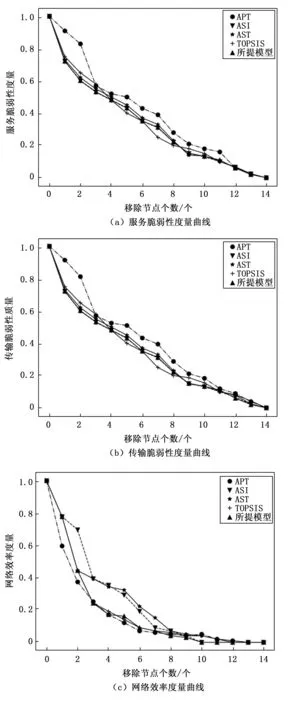
图2 不同模型删除节点的脆弱性曲线
综合以上分析,所提多层节点重要性识别模型可综合考虑物理拓扑层、传输层、服务层中各节点重要性度量,从而高质量确定电力通信网络中重要节点。仿真结果符合实际情况,验证了所提模型的有效性和实用性。
4 结束语
本文对智能电网中电力通信网络进行了研究与分析,建立了一种基于多层节点重要性的电力通信网络节点识别模型。该模型将电力通信网络分为3个网络逻辑层:物理拓扑层、传输层和服务层,并通过综合分析并明确三层中的节点影响电网运行的状况、通信网络性能、节点长期平均重要性。
所提多层节点重要性识别模型的可为电力通信网络分析与电力领域安全发展提供一定借鉴作用。
