WSN中基于超椭圆判决边界的异常检测的动态建模
2023-10-28方小明刘艳梨
方小明,刘艳梨
(江苏安全技术职业学院 电气工程学院,江苏 徐州 232001)
0 引言
在有线感知基础设施部署过于昂贵或不能实现的环境中,无线传感器网络(WSN,wireless sensor network)为监测和数据收集提供了一个成本高效的平台[1-2]。WSN由一组节点构成,每个节点都配备一组感知设备。在每个节点上安装不同的感知元件(如温度和湿度传感器),使得WSN能够收集大量多维的和相关的样本。WSN的一个重要挑战是检测由周围环境中感兴趣的事件或节点故障引起的异常测量值。在节点上发现异常测量值,使得我们可以通过减少网络上原始数据的通信,节省无线节点的有限资源。为了检测异常,需要对节点的行为进行建模。
人们提出了各种数据挖掘方法来建立节点的行为模型。在分散式方法中,WSN中的每个节点都建立一个自身正常行为的局部模型,将局部模型的参数转发到基站或簇头,然后根据局部模型计算全局模型。近年来,人们提出了许多采用这种方法的不同数据建模方法。然而,这些模型大多为静态模型,不能适应环境中的变化。此外,这些模型的准确性依赖于初始训练周期的正确选择。如果初始训练周期不能很好地代表将来的测量值,模型就是失败的。因此,重要的问题是如何持续学习非平稳环境中的行为模型,即如何检测非平稳环境中的异常事件。
异常检测是WSN中一个活跃的研究课题。在WSN中,异常检测技术已应用于许多方面,包括入侵检测、事件检测和质量保证[3-5]。在这些应用中,有许多因素会影响异常检测的使用,如传感器的移动、环境条件(有利的或不利的)、环境的动态性和能量约束。因此,异常检测技术在实际应用中的一个关键问题是如何将其推广到具有动态变化的在线数据流中。
文献[6]提出了一类支持向量机(SVM,support vector machine)模型来发现WSN数据中的异常现象。这种方法主要假设所有的训练数据都可以在传感器上获得,并且训练以批处理的方式进行。尽管这些方法可以为正常数据提供良好的决策边界,但它们对于每个传感器有很高的计算开销;文献[7]提出了一种基于长短期记忆网络自编码(LSTM-Autoencoder)的网络流量异常检测方法,将真实网络流量从数据包和会话流级别两方面提取数据特征,采用离散小波变换(DWT,discrete wavelet transform)分解原始特征向量得到更高维特征,用已训练的LSTM-Autoencoder模型对训练数据进行重构,通过分析重构误差分布确定检测阈值。该方法的主要缺点首先是训练对数据中的噪声敏感,其次很难理解是什么触发了报告的异常;文献[8-9]把超椭圆边界用来建模系统的正常行为与批处理训练。这种方法允许训练数据中存在噪声,并向用户报告个别异常。然而,其超椭圆边界是在一个训练周期上计算的,而且要求节点在训练期间将测量值保存在存储器中,在训练结束时所有的测量值以批处理方式处理。尽管这些方法在计算上是高效的,但它们不能适应环境中的变化,是一种静态模型。作为比较,本文将这种方法称为静态数据捕获异常检测(SDCAD,static data capture anomaly detection);文献[10]提出了一种基于四分之一超球SVM算法的异常数据检测方法,利用从传感器节点中收集到的原始数据建立支持向量机预测模型,并结合粒子群算法找出最佳参数,然后利用最佳参数对原本的模型进行优化;文献[11]提出了一种新的时间-空间-属性单类超球面支持向量机来建模WSN中的异常事件检测问题,并提出了在线和部分在线离群点检测算法。但部分在线离群点算法在训练和更新时需要大量的计算;文献[12]提出了一种累积和(CS,cumulative sum)算法来检测网络异常。尽管基于CS的异常检测算法计算效率高,但基于其阈值的检测机制通常不能准确地建模正常行为;文献[13]提出了数据流自回归模型的迭代估计,并采用CS作为在线异常检测;对于多维数据中的异常检测是著名的批(子群)处理技术,它采用马氏距离[9,14-15]进行异常检测;文献[16]提出了一种基于改进压缩感知(CS,compressed sensing)重构算法和智能优化GM(1,1)的WSN异常检测方法。首先通过建立双层异质WSN异常检测模型,并采用压缩感知技术对上层观测节点收集到的下层检测节点温度测量数据进行处理,同时结合温度数据稀疏度未知特点,构造有效的稀疏矩阵和测量矩阵,并重新定义测量矩阵正交变换预处理策略,使得CS观测字典满足约束等距条件;其次,重新定义离散蜘蛛编码方式,蜘蛛种群不断协同进化,以获得稀疏结果中非零元素的位置信息,利用最小二乘法得到非零元素的幅度信息,实现对未知数量检测节点数据的精确重构,在此基础上采用蜘蛛种群迭代进化得到优化后GM(1,1)的参数序列,通过检测参数序列的相关阈值来判定节点是否发生异常;文献[17]提出了一种基于传感器网络时间序列数据的检测方法,方法利用传感器采集的K个正常数据的中位数建立枢轴量,构造置信区间,并提出了一种计算数据区间差异度的方法来判断发生异常的来源。实验结果表明,该方法对传感器网络的异常数据检测率保持在98%以上,误报率保持在0.5%以下,具有一定的实用性;文献[18]提出一种基于平衡迭代规约层次聚类(BIRCH,balanced iterative reducing and clustering using hierarchies)的WSN流量异常检测方案。该方案在扩充流量特征维度的基础上,利用BIRCH算法对流量特征进行聚类,并通过设计动态簇阈值和邻居簇序号优化BIRCH聚类过程来提高算法的聚类质量和性能鲁棒性。进一步设计了基于拐点的综合判决机制,结合预测,聚类结果对流量进行异常检测,以保证方案的检测准确性;为了提高无线传感网络的鲁棒性,针对目前的网络漏洞检测方法无法计算出相邻节点的相对位置信息,存在无线传感器网络漏洞检测误差大的问题,文献[19]提出了先利用覆盖漏洞发现算法组建传感器极点坐标,获取最相近节点间位置信息,计算出任意节点被其最相近节点覆盖的边缘弧信息序列,然后得到对应传感器节点间需要增加的新传感器数量,从而实现无位置信息的无线传感器网络漏洞检测方法;文献[20]针对WSN中传感器自身安全性低、检测区域恶劣及资源受限造成节点采集数据异常的问题,提出了一种基于图信号处理的WSN异常节点检测算法。算法首先依据传感器位置特征建立-近邻图信号模型,然后基于图信号在低通滤波前后的平滑度之比构建统计检验量,最后通过统计检验量与判决门限实现异常节点存在性的判断。通过在公开的气温数据集与PM2.5数据集上的仿真验证结果表明,与基于图频域异常检测算法相比,在单个节点异常情况相同条件下,所提出的算法检测率提升了7个百分点。在多个节点异常情况相同条件下,其检测率均达到98%,并且在网络节点异常偏离值较小时仍具有较高的检测率。
为了实现WSN中动态数据流环境的异常检测,本文提出了一种迭代方法来建立超椭圆判决边界,其中每个节点基于到当前时间为止的测量值来调整其超椭圆模型,本文将提出的这种方法称为动态数据捕获异常检测(DDCAD,dynamic data capture anomaly detection)。当边界参数变化较小时,DDCAD算法终止;同时,还提出了一种遗忘因子方法来提高模型在非平稳环境中的跟踪能力;仿真实验结果表明,提出的方法通过适应环境中的变化,在非平稳环境中比现有的批处理方法能够获得更高的准确性,更适合于实际应用。
1 动态数据流环境下的迭代超椭圆边界算法
首先给出描述异常检测超椭圆模型所需的定义。令Xk={x1,x2,…,xk}为一个WSN中的一个节点在时刻{t1,t2,…,tk}的前k个样本,其中每个样本是Rd中的一个d×1向量。向量中的每个元素表示由节点测量的感兴趣的属性,如温度和相对湿度。Xk的样本均值mk和样本协方差Sk计算如下:
(1)
(2)
以具有协方差矩阵Sk的、以mk为中心的有效半径t的超椭圆定义为:
(3)
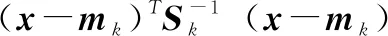
超椭圆ek的边界定义为:
(4)
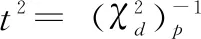
定义1:将关于ek的单点一阶异常定义为在其外面的任意数据向量x∈Rd,即对于ek来说:
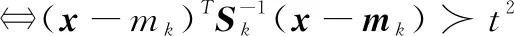
(5)
已知节点在tk的样本,要处理节点上的下一个样本。在tk+1,我们记录测量向量xk+1∈Rd。首先,用式(5)来测试xk+1,然后用它来增大ek。如果xk+1∉ek,就声明它是一个异常,并将它发送给基站进行进一步处理。特征矩阵迭代更新公式为:
(6)
(7)
我们采用S-1=I(其中I是单位阵),而不采用从前几个样本获得的估计值来初始化迭代方法,因为前几个样本通常会产生一个奇异的样本协方差矩阵。
我们用正常和异常测量值来增大ek。假设大部分数据都是正常的,因此可以抵消用异常测量值进行更新的任何不希望的影响。然而,也可以设计更复杂的方法,以不同的方式处理异常。这时应考虑异常是否是环境中的正常变化(漂移)。这类分析需要额外的输入来确定异常的类型。
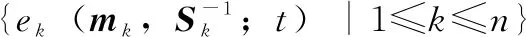
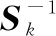
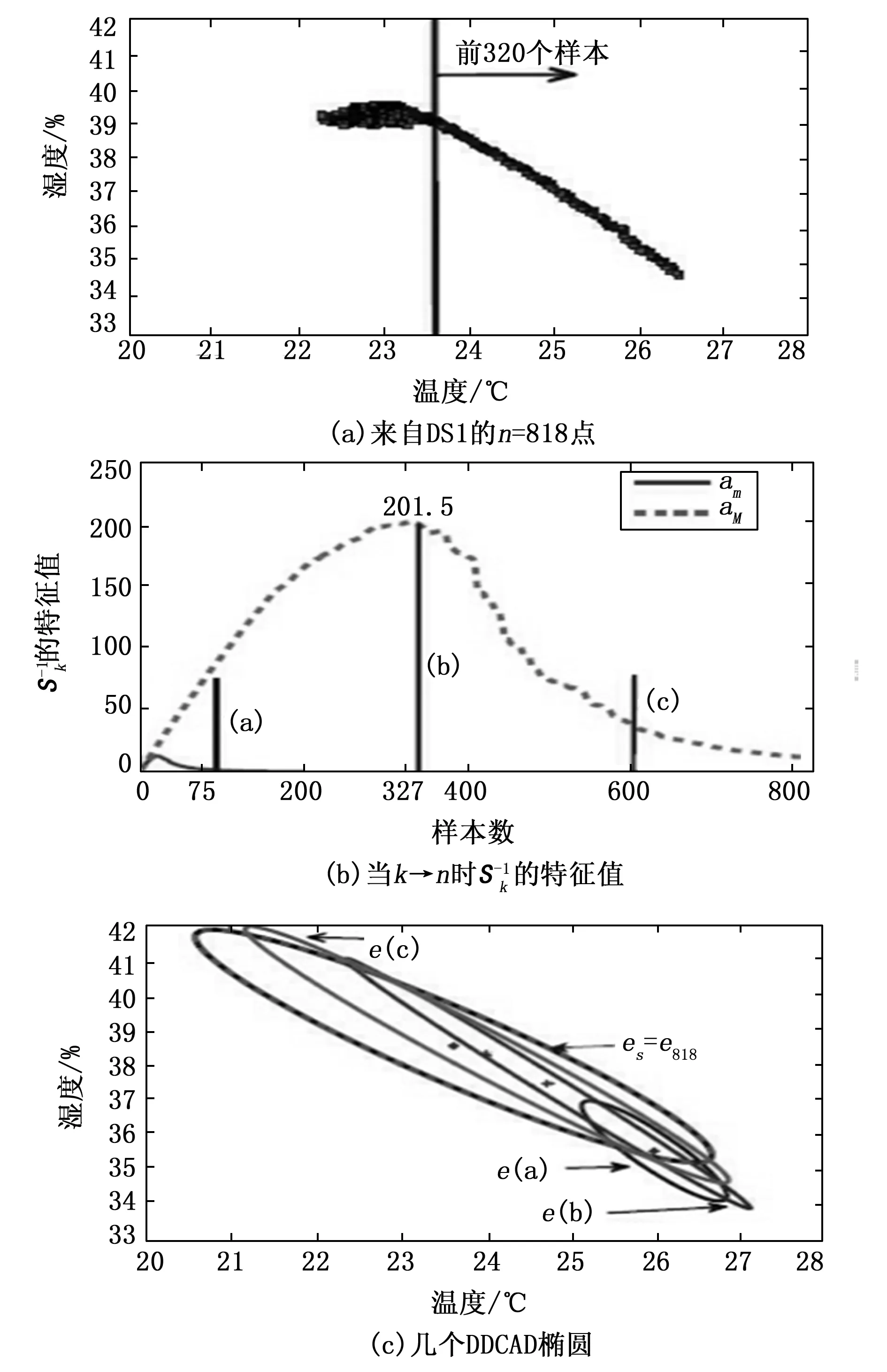
图1 DDCAD序列ek收敛到其最终状态e818=es
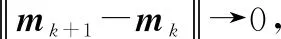
2 采用遗忘因子的跟踪能力
为了使DDCAD算法能够跟踪监测环境中的数据变化,我们为旧的测量值引入遗忘因子。通过引入遗忘因子0<λ
mk+1,λ=λmkλ+(1-λ)xk+1
(8)
对于k个样本,采用指数遗忘因子λ的加权样本协方差为:
(9)
首先要找到考虑遗忘因子的迭代协方差矩阵更新公式,然后得出特征矩阵的迭代更新公式。通过整理式(9),可以基于上一步的协方差矩阵加上一个更新值,写出k+1时刻的协方差矩阵的更新公式。式(10)为协方差矩阵的一步更新:
(10)
将式(10)中的mk+1替换为式(8)中mk+1可得:
(11)
为了计算特征矩阵的更新公式,我们用矩阵逆引理式(12)来求两个矩阵的和的逆。假设E是可逆的且B是一个方阵。注意,在本文中,E是一个数,C和D是向量。将这个引理应用到式(11)中,经过重新整理,得到式(13):
(B+CED)-1=B-1-B-1C(E-1+DB-1C)-1DB-1
(12)
(13)
把用式(8)和式(13)对ek的更新序列称为遗忘因子DDCAD(FFDDCAD,forgetting factor DDCAD)。

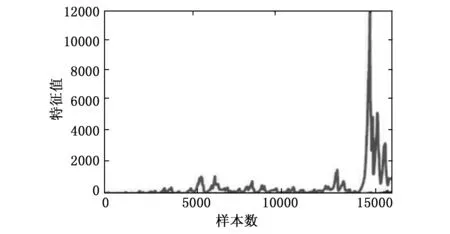
图2 采用FFDDCAD在每次更新后特征矩阵的特征值
2.1 采用滑动窗口的基准估计
为了限制FFDDCAD更新公式中k的增长,可以在大小为w的滑动窗口上采用FFDDCAD。为了提供比较基准,从窗口开始重新计算总体估计,以便在每次输入后得到准确的FFDDCAD椭圆。对于在线算法来说,尽管这种方法的计算效率不高,但它提供了采用主动测量值的超椭圆边界的精确值(即在滑动窗口中的测量值),并用作基准,作为比较在计算中限制大k效应所提出的方法。
2.2 有效N跟踪方法
在这种方法中,为了解决跟踪k较大的问题,当k≥neff时,我们简单地用不变的neff来代替式(13)中的k。其思想是在k≥neff后,分配给数据样本的权重趋于0,即λk≌0,因此相应的样本几乎被完全遗忘。在本文中,取neff=3τ,其中τ=1/(1-λ)为具有指数遗忘因子λ的迭代算法的记忆范围。基准方法和有效N跟踪方法的示意如图3所示。方框所示为在椭圆边界计算中所考虑的样本。在有效N跟踪方法中,旧样本的权重按指数下降。
1.英语中有些以a-为词首的表语形容词如asleep,awake,alive修饰名词时须放在其所修饰的名词后做后置定语。例如:
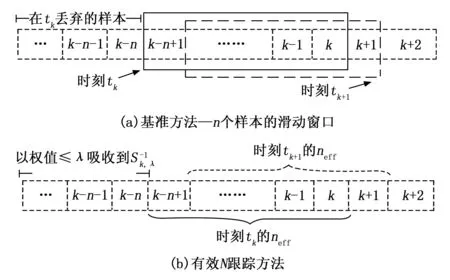
图3 在样本k和k+1的基准方法和有效N方法的示意图
2.3 计算复杂度讨论
在计算复杂度方面,SDCAD、DDCAD和FFDDCAD都需要对数据进行一次遍历,所以它们的计算复杂度都随n线性增长,有渐近复杂度O(nd2);迭代方法(DDCAD和FFDDCAD)以在线处方式处理数据,具有恒定的存储复杂度,而SDCAD方法的存储需求随n线性增长;采用有效N跟踪的FFDDCAD准确性和效率使得其适合于在线流数据分析,特别是在WSN中。
3 仿真实验
本节首先给出在评价不同方法时采用的数据集,然后比较提出的采用有效N方法和基准方法的FFDDCAD,并比较了两种FFDDCAD方法在合成数据集上的检测率和误报率。在合成数据集中,将[-10 10]上的均匀噪声随机加入到1%的样本中,并将这些样本标记为异常,而其他剩余的样本视为正常。另一种比较方法是基于与提出的基准方法的偏差而引入的,这种方法不需要标记数据集,因此允许采用实际的数据集进行比较。接下来,我们比较了FFDDCAD相比于SDCAD在异常检测上的效果。最后,我们比较了本文提出的采用有效N方法的FFDDCAD与和文献[13]中提出的变化检测技术。
3.1 数据集
采用3个数据集来评价本文提出的异常检测迭代模型,并将其与现有的静态方法进行比较。第一个数据集(称为DS1)由某院校物联网研究实验室的54个传感器收集的测量数据构成;第二个数据集(称为DS2)是从部署在某市城市道路之间的23个交通传感器收集的数据;第三个数据集(称为DS3)是由部署在某市小镇的森林中的16个传感站收集的数据。图4为3个数据集的散点图。
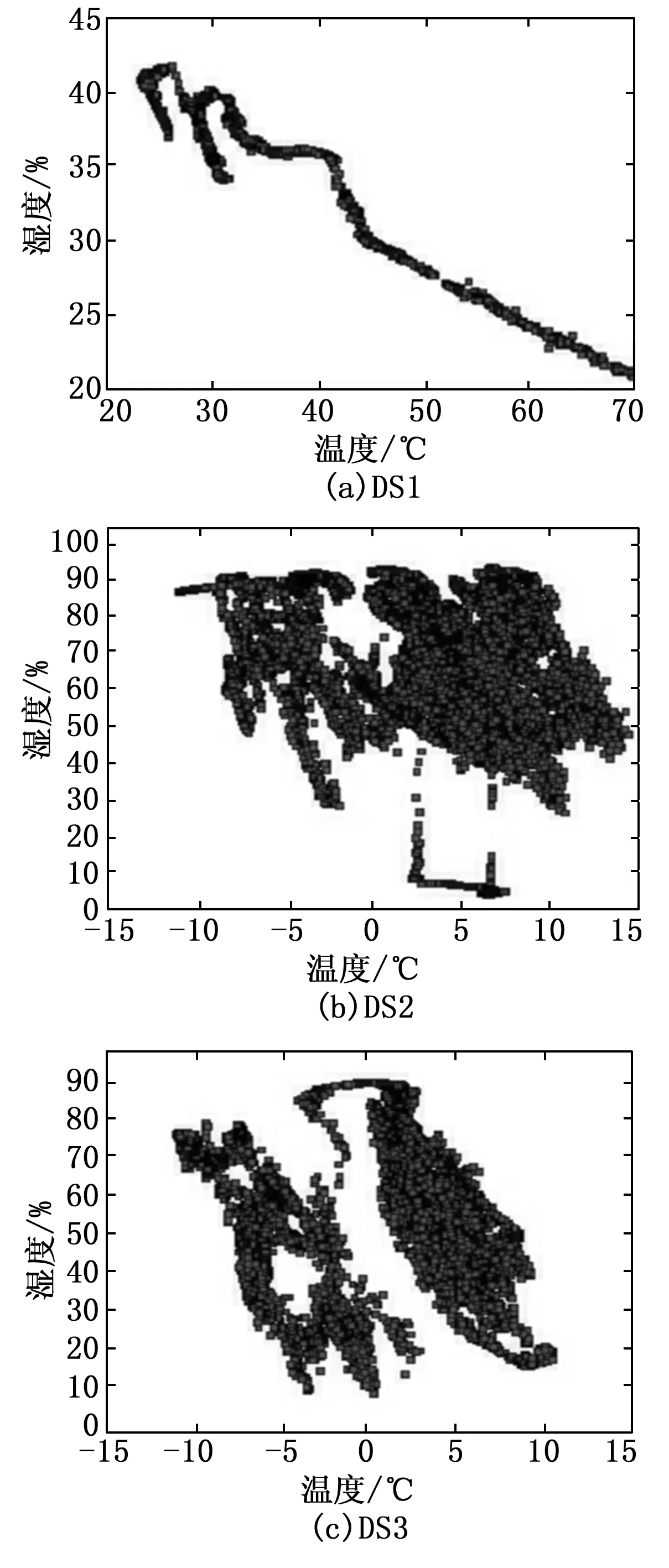
图4 用于评价的数据集的散点图
通过考虑具有不同正态分布N(∑1,μ1)和N(∑2,μ2)的M1和M2两种模式的两个合成数据集SDS1和SDS2如图5所示。模式M1和M2的参数值如表1所示。M1为初始模式,M2为最终模式。M1的变换如下。

表1 用于生成合成数据集的两个正态分布的参数
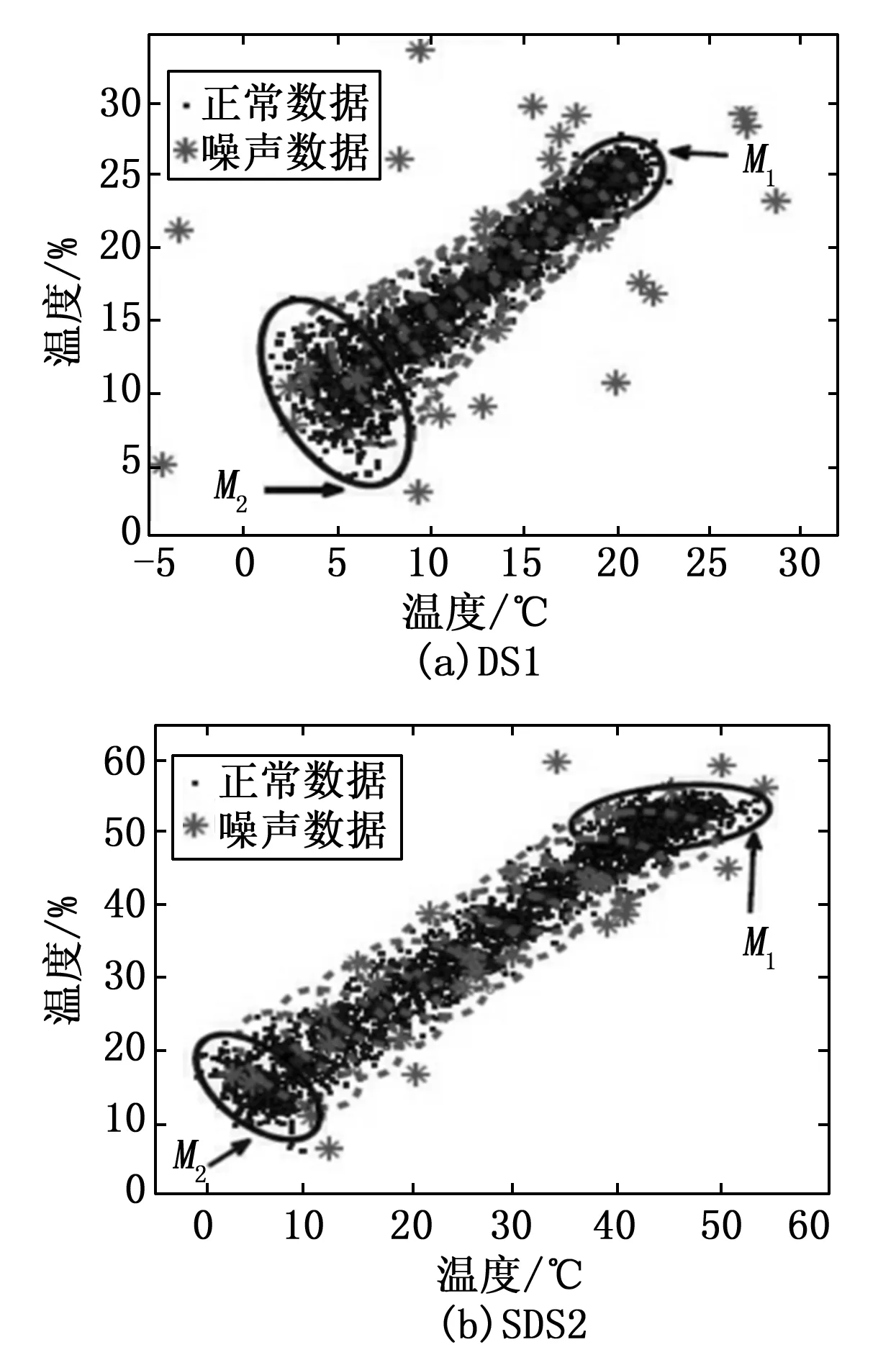
图5 用于评价的合成数据集的散点图
3.2 DDCAD的收敛性
运行第2节中提出的DDCAD方法,并将其与计算整个数据集的协方差矩阵和均值的批处理SDCAD方法[9]进行比较。采用焦距(两个椭圆之间的距离的量度)来检查DDCAD的最终椭圆边界与SDCAD的距离有多近。焦距考虑了两个椭圆的形状和位置,结果如图6所示。图6中点构成的虚线椭圆为DDCAD得到的最终椭圆,实线构成的椭圆为采用SDCAD方法得到的最终椭圆;可以看到,DDCAD算法和SDCAD算法的最终结果非常相似,两个最终椭圆之间的焦距即FD(en,ens)非常小,对于DS1为0.001 6,DS2为0.001 4,DS3为0.002 4。这些小的距离并没有对最终的边界产生视觉上的明显影响。
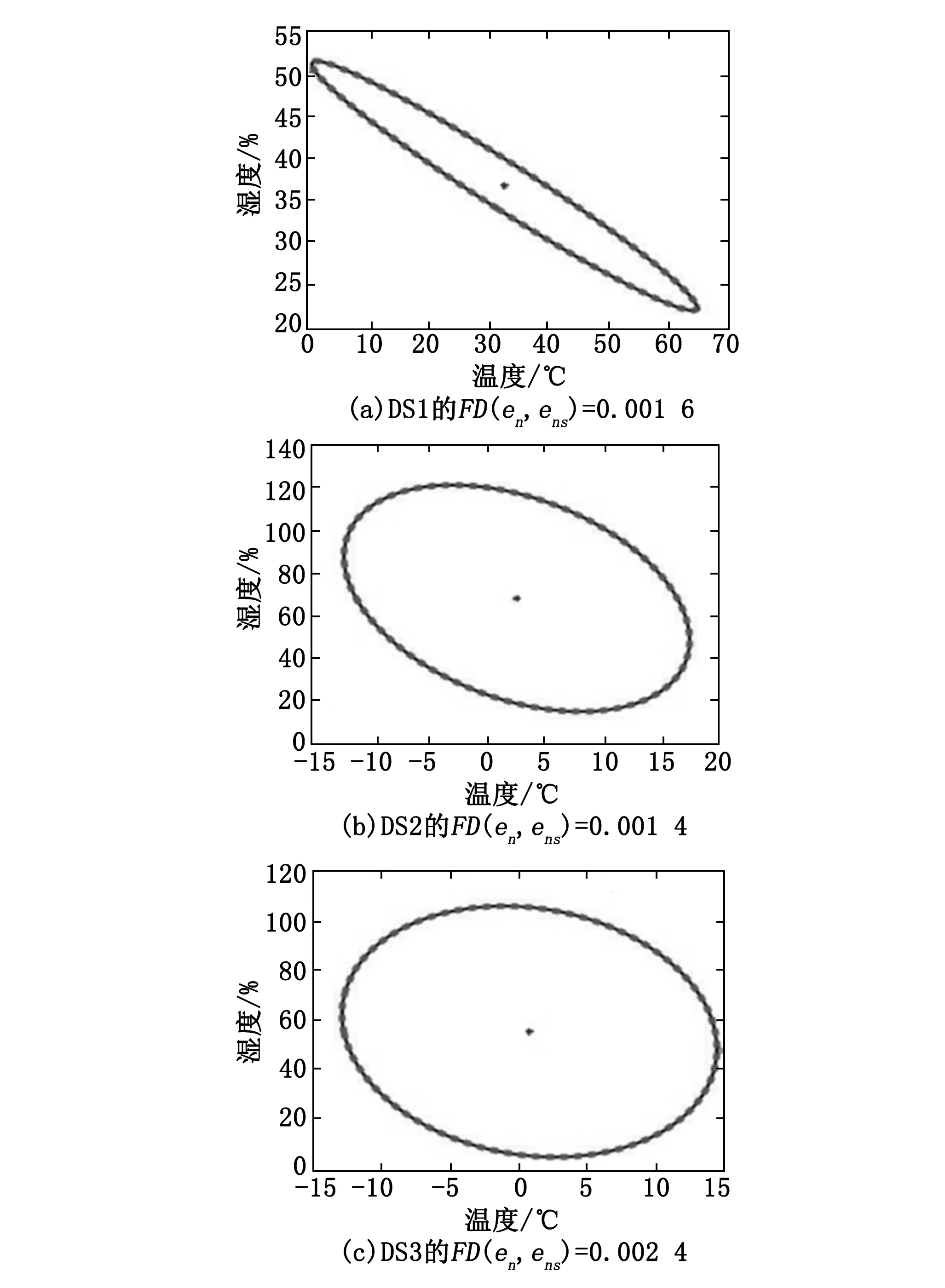
图6 采用DDCAD和SDCAD得到的最终椭圆边界与相应的焦距
3.3 跟踪能力的比较
为了比较提出的跟踪方法,我们首先用合成数据集来比较所提出的异常检测模型的准确性。对于基准方法,考虑300个样本的窗口大小。同样,neff设置为300个样本。表2所示为两种跟踪方法的检测率和误报率,其中DR表示检测率,FA表示误报率。可见,有效N跟踪方法具有与基准方法相当的准确性。这说明有效N跟踪方法是基准方法的良好近似,neff可以代替跟踪迭代公式中的k来当解决k变大时的不稳定性问题。
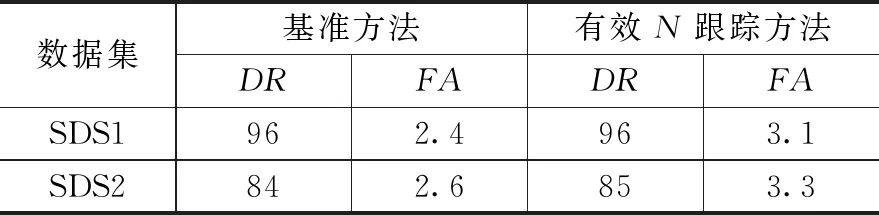
表2 不同跟踪方法在合成数据集上的比较
3.4 异常检测能力的比较
我们对两个合成数据集SDS1和SDS2比较采用有效N跟踪方法的FFDDCAD和文献[9]提出的SDCAD方法,得到的检测率和误报率如表3所示。可见,在代表非平稳环境的这两个数据集中,采用有效N跟踪方法的FFDDCAD比批处理的SDCAD方法有更高的准确性。这是因为用于批处理学习的数据不是来自单个分布,所以正态性假设很弱,从而导致模型无法检测异常。

表3 异常检测能力的比较 %
3.5 数据流中的变化检测
本节比较了本文提出的FFDDCAD方法与文献[13]的方法用于数据流的在线异常检测。在数据流分析中,通常采用动态预测模型和残差分析(如CS)来检测数据流中的变化或异常。为便于比较,我们不直接采用文献[13]的方法,而是采用递归最小二乘(RLS,recursive least squares)迭代建立以湿度作为输入(激励信号)的温度预测的自回归各态历经(ARX,autoregressive eXogenous)模型,阶数为np=4,并对其残差应用CS来发现数据流的变化。FFDDCAD的定义是发现单点异常,并且可以很容易地修改来检测变化点。当FFDDCAD模型在数据流中发现na个连续的单点异常时,它可以发出变化信号。
由于在实际的数据集中缺乏基本的真实性,这使得很难解释变化的点。因此,这里我们仅采用DS1和两个合成数据集来比较两种方法的结果。ARX/RLS和FFDDCAD在初始状态时都视为是不准确的,因此,延迟采用这两个模型对初始化后的前nd=50样本进行异常检测。注意,在每个变化点之后,模型重置回其初始状态。
图7为ARX/RLS方法和FFDDCAD方法对于数据流变化检测的结果,加号表示变化点;可见,FFDDCAD方法和ARX/RLS方法对于DS1的性能是相当的,但采用FFDDCAD方法可以检测到更多的变化点,表明FFDDCAD方法优于ARX/RLS方法;而对于SDS1,ARX/RLS方法不能发现模式之间的变化点,而FFDDCAD方法可以检测到5个变化点;在SDS2中,FFDDCAD方法可以检测所有模式变化,而ARX/RLS方法仅检测到一个模式变化;总之,FFDDCAD方法对于数据流变化的检测始终优于ARX/RLS方法。
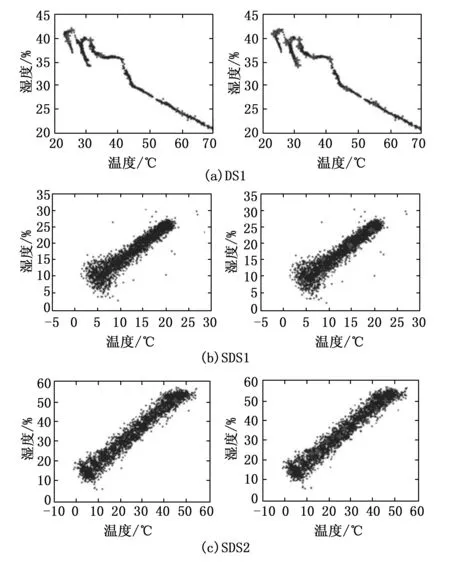
图7 ARX/RLS(左)与FFDDCAD(右)对于数据流分析和变化点检测的比较
4 结束语
本文针对WSN中的异常检测提出了一种迭代模型,其迭代性使得它更适合于流数据分析;此外,在模型中引入遗忘因子,使其适合于非平稳环境;评价表明,提出的方法可以密切跟踪环境中的变化,在非平稳环境中能获得比批处理方法更好的准确性。同时在数据流的异常检测中,本文提出的采用遗忘因子的FFDDCAD可以更好地检测环境中的变化,计算复杂度也比目前先进的方法更低。
