基于改进人工蜂鸟算法的VRV空调需求响应功率削减策略
2023-10-28陈羽飞闫秀英
陈羽飞,闫秀英,门 琪
(西安建筑科技大学 建筑设备科学与工程学院,西安 710055)
0 引言
随着经济的快速发展,社会总电力需求日益增加,夏季高峰负荷逐年上升,给电网的安全稳定运行带来了挑战[1]。其中空调负荷是夏季高峰负荷的主要组成部分,具有数量多、潜力大、灵活可控以及调控效益大等特点,因此被看作是重要的负荷调控资源[2]。在夏季用电高峰时期,空调设备的大规模使用以及用户对空调设定温度的随意调节等行为会加剧建筑能源的消耗,同时也会增大电力系统的负担,严重则会威胁电网的安全,因此对于建筑中空调设备在夏季负荷高峰时期的调控策略的研究是十分有必要的。需求响应是一种有效的需求侧负荷控制手段[3],分为基于价格和基于激励两种调控方式[5]。在空调负荷参与电网调控的研究中,除了要考虑用电功率的削减以及用电负荷的转移等用户用电行为模式的改变[6],还要考虑用户的意愿、舒适度以及调控的成本与效益等因素[7]。
关于空调优化调控策略的研究中,大多都是先对空调负荷按特定指标进行数学仿真建模[8-9],常见的指标有空调能耗[10]、室内温度[11]、用户舒适度[12]以及用电费用[13]等,再结合所制定的目标函数与约束条件构建优化模型,最后利用相关优化算法对模型进行求解。元启发式算法(Meta-heuristic algorithm)是基于计算智能的机制求解复杂优化问题最优解的方法,也被称为智能优化算法。随着计算机网络与人工智能技术的发展,其逐渐被应用到空调系统优化调控策略的制定中。李楠等[14]提出了一种基于非支配排序的粒子群优化算法,并结合克里金方法对典型办公房间的暖通空调系统进行优化。孙宏昌等[15]提出了一种结合并行时间卷积神经网络和改进黑猩猩优化算法的控制策略,可以在保持室内热舒适的同时实现能耗节约。杨思远等[16]提出了一种改进的并行人工免疫系统算法来确定系统在不同负载下的最优运行参数,以最大限度地提高系统的运行能效。J.L.Chiuhsiang等[17]提出了一个基于多目标鲸鱼优化算法的优化模型来平衡空调加机械通风系统的能耗和热舒适,模型实现了16.51%的能耗降低和49.06%的舒适度提升。但目前智能优化算法的应用大部分是在空调系统的正常运行工况下,在与电网需求响应调控指令的结合上还不是很多,而且大多数研究只考虑到用户侧的效益,对负荷聚合商的经济利益考虑得不够全面。并且智能优化算法在解决“多变量、多目标、多约束”的实际工程应用问题中的收敛性能与求解精度方面有待进一步提高。
本文以某办公建筑变制冷剂流量(VRV,variable refrigerant volume)空调系统为研究对象,综合考虑用户舒适度、负荷聚合商利益以及需求响应调控效果这3个方面,针对夏季需求响应期间办公建筑空调系统的功率削减展开研究。空调在制冷工况下通过适当的升高温度设定值可以降低空调功耗,考虑到建筑内不同区域的差异性以及不同用户对温度的需求,提出基于不同舒适度的温度控制档位。为了充分调动用户参与需求响应的积极性并发挥用户的“体验价值”,提出用户不满意百分比的概念,并以此为依据为每个控制档位制定不同的激励电价。以功率控制偏差和激励费用最小为目标,空调运行特性和用户舒适度为约束,构建基于室内机温度分档控制的多目标优化(ITSC-MOO,indoor units temperature staging control - multi-objective optimization)模型。提出了一种混合Hammersley序列初始化和高斯变异扰动的改进人工蜂鸟算法(HAGSAHA,hybrid hammersley sequence initialization and Gaussian variation perturbation of artificial hummingbird algorithm)。运用HAGSAHA对优化模型进行求解,并与人工蜂鸟算法(AHA,artificial hummingbird algorithm)、粒子群算法(PSO,particle swarm optimization)、灰狼优化算法(GWO,grey wolf optimization algorithm)和鲸鱼优化算法(WOA,whale optimization algorithm)的优化求解结果进行对比,以证明所提策略的有效性。
1 空调模型建立
1.1 研究对象介绍
选用西安市高新区某办公建筑VRV空调系统为研究对象,其系统如图1所示。整个系统采用R410A环保冷媒作为制冷剂,压缩机采用全封闭涡旋式直流变频压缩机。系统共由2台室外机和30台室内机组成(共30个空调房间,每个房间配有一台室内机)。室外机和室内机的连接采用“一拖多”的形式,其中一台室外机连接14台室内机,另一台室外机连接16台室内机。表1为空调室外机和室内机的详细设备参数。

表1 多联机空调系统设备参数
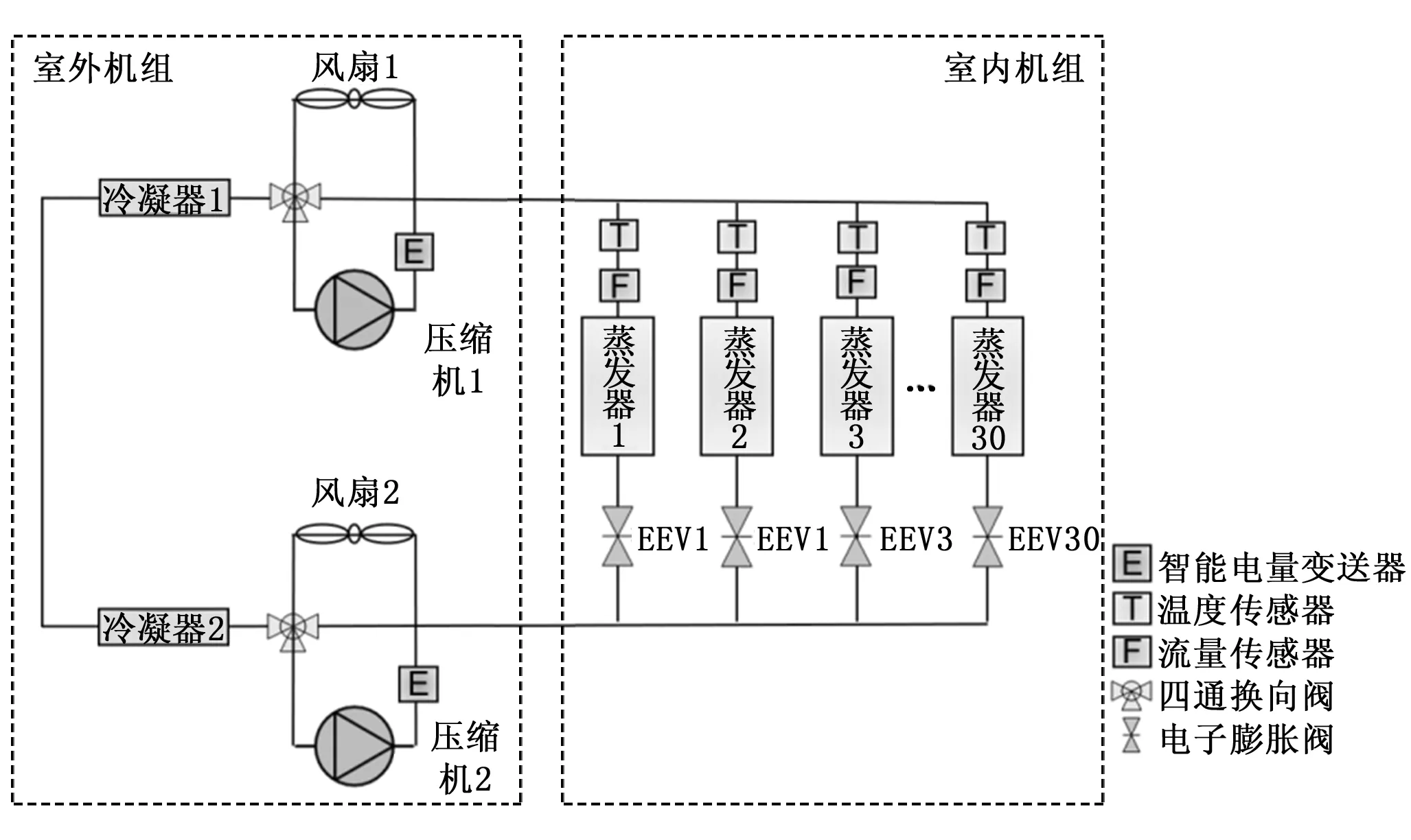
图1 某办公建筑多联机空调系统图
1.2 EnergyPlus物理仿真模型建立
1.2.1 建筑模型建立
结合研究对象的建筑设计图纸,使用SketchUp软件建立该办公建筑的三维模型并赋予其热工属性,如图2所示。并在EnergyPlus软件中设置组成建筑围护结构材料相关参数。表2给出了组成建筑围护构件材料的尺寸和热特性。
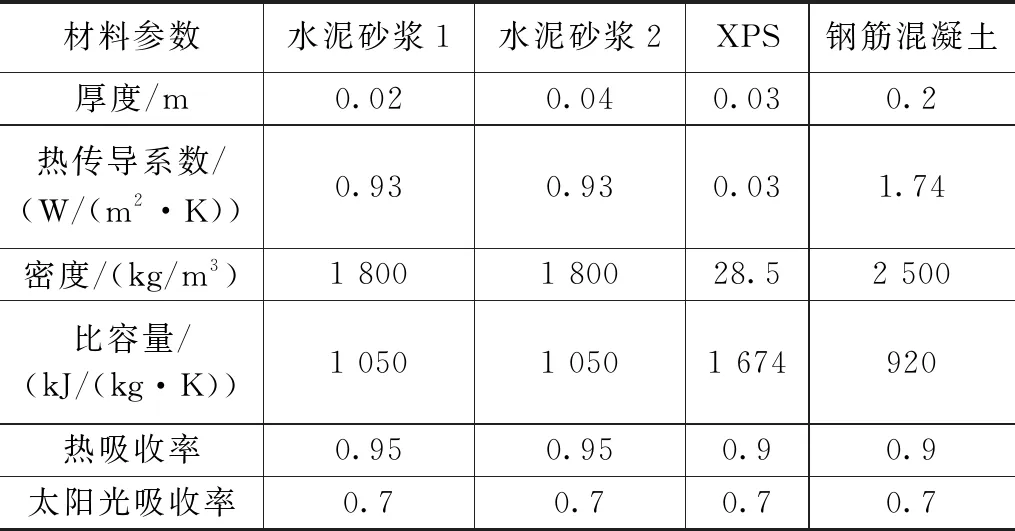
表2 建筑材料相关参数
图2 办公建筑的三维模型图
1.2.2 空调系统参数设置
利用EnergyPlus中已有的风冷型DX(direct expansion直接膨胀式)盘管充当室内机组,为建筑物各区域提供冷热量,将表征其制冷(热)量及功率的特征曲线用研究对象VRV系统室内机的性能曲线进行替换(性能曲线从空调产品手册中获得),并参照表1设置额定功率/制冷量等相关参数。用同样的方法设置室外机相关参数,最终建立室外机与室内机之间的连接关系。
1.2.3 室内热扰设置
为了更真实地反映出建筑内部的实际热扰情况,包括人员数量、室内风速、灯光强度以及电力设备的功率,在EnergyPlus中进行室内环境及热扰等参数的设置。根据实际调查结果,按照办公建筑内部区域在人员数量和使用功能上的差异将建筑内所有房间分为了四类,分别是:Zone1(综合服务性区域)、Zone2(办公区域)、Zone3(人少的办公区域)、Zone4(活动区域)。在软件中的“People”、“Lights”、“Electric Equipment”、“ZoneInfiltration:DesignFlowRate”4个模块中按表3~4中的参数进行室内热扰及人员舒适度的设置。

表3 室内热扰参数设置

表4 人员热舒适参数设置
1.3 仿真模型验证
建立好的模型需要进行准确性检验,可以用来检验准确性的参数有很多,常用的有负荷、功耗、能耗等。检验参数的时间间隔可以是月、日、小时等。在模型准确性验证时,被广泛接受的是 ASHRAE 14-2014标准[20]。在 ASHRAE 14-2014 标准中,归一化平均偏差(NMBE)和均方误差变异系数(CVRMSE)是两个常用误差评价指标,具体表达式分别为式(1)和式(2)。该标准规定,如果以逐时数据进行验证,要求逐时的NMBE小于±10%以及CVRMSE小于±30%。
(1)
(2)

在 2021 年夏季制冷季对该建筑空调的功耗数据进行收集,总共收集 180组(每天9组,共20天)逐时功耗数据。其中,有169组数据空调设定温度为24 ℃,因此模型仿真中的设定温度按24 ℃进行设置。模拟期间所用到的天气文件按照数据采集期间实际的气象数据进行修改,模拟在EnergyPlus9.0.1软件中进行。图3展示的是空调功耗模拟值与实际值的对比情况,两者的计算误差值结果如表5所示,由此可看出模型的两种误差指标均在规定的误差范围内,表明所建立的仿真模型是合理的。

表5 模型验证结果 %

图3 空调功耗模拟值与实际值对比
1.4 VRV空调功耗数学模型建立
空调功耗数学模型的建立包含空调房间的热力学建模和空调系统的能效建模两方面内容。前者主要描述了室内温度与空调制冷(热)量的时变关系;后者则建立了制冷(热)量与功耗之间的数学关系,将二者结合则可建立起室内温度与空调系统功耗的联系。
1.4.1 房间热力学模型
空调房间的热力学原理采用等效热参数(ETP,equivalent thermal parameter)模型[21]描述,将其简化成一阶方程,可以得到房间温度与空调制冷量的时变关系如下:
(3)

1.4.2 VRV功耗模型
VRV空调系统的运行功率主要由机组制冷量以及能效比(EER,energy efficiency ratio)决定[22],如式(4)所示。EER 主要由空调室外机的部分负荷率(PLR,part load ratio)决定,VRV空调的部分负荷率定义为某时刻的室内机制冷量之和与室外机额定制冷量的比值,通常可按式(5)进行描述:
(4)
式中,Qindoor,w为第w台的室内机的制冷量,Qindoor,all是指所有室内机制冷量之和,n为室内机台数。
(5)
式中,a、b、c、d为模型待拟合系数,Q0为室外机额定制冷量。
通过1.2节建立的物理仿真模型对空调在夏季典型工况下的运行情况进行模拟,得到的办公建筑空调系统运行的数据,将其用作对模型参数的辨识。一共模拟出300组逐时数据,选择一半用于模型参数的辨识,另一半用于对辨识结果进行验证。通过 Matlab 软件采用最小二乘法对模型参数进行辨识,从而得出VRV空调能效比EER与部分负荷率PLR的函数关系。辨识及验证结果如表6所示。
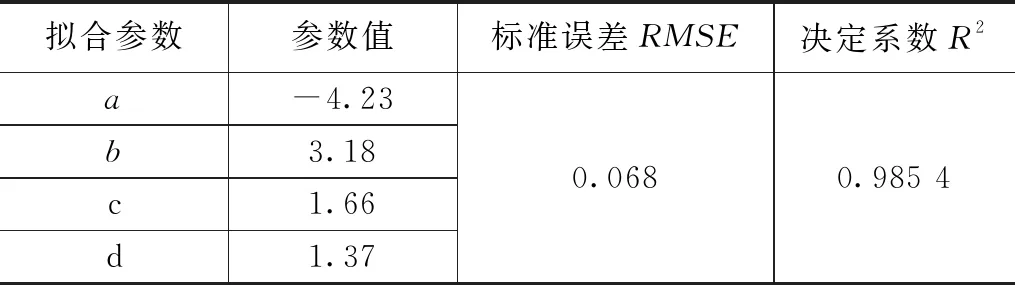
表6 EER 与 PLR 的拟合系数及精度拟合结果
因此VRV空调的功率PAC表达式如下:
(6)
由此可看出,VRV系统室内机的制冷量之和将直接影响机组部分负荷率,进而影响机组能效比的大小,二者共同决定了机组的运行功率。
2 室内机温度分档控制模型
2.1 控制方案制定
需求响应过程中,在保证舒适度要求的前提下,空调的室内温度设定值可以在一定范围内提高,从而降低机组运行功率,最终达到响应目标。结合多联式空调机组的特点,改进传统的温度控制方式,制定 VRV 室内机温度分档调控多目标优化模型。模型能够根据优化目标,结合电网的功率削减指令对空调用户所受控的档位进行合理安排与调整。假设所有房间室内机在受控前的初始温度设定值为 24 ℃,考虑到不同用户对于室内舒适度需求的差异,将温度控制方案按设定温度不同分为四挡,第一档的温度设定值为 25 ℃,以每档提高 1 ℃ 依次递增。
为充分调动用户参与需求响应的积极性,在用户参与需求响应的过程中,负荷聚合商应对用户进行相应的激励补偿。由于不同控制档位下用户的“体验感”不同,因此对不同档位所设置的激励价格也应存在差异。为了更加突出用户对空调服务的“体验”价值,现针对不同档位的人体热舒适差异分别制定不同激励价格。
人体热舒适可通过预测平均投票(PMV,predicted mean vote)来表征[12]。表7为人体热感觉标尺,理想的热舒适范围应在 [-0.5,0.5]范围内。为了解用户在不同档位下的热舒适情况,在EnergyPlus中进行不同档位下人体热舒适的模拟。在“People”模块中完成对热舒适相关参数的设置,见1.2.3节。在Output:Variable中选择变量“Zone Thermal Comfort Fanger Model PMV”输出得到 PMV 逐时数据,模拟时间段选取典型年7月1日—7月31日,4个档位的设定温度按表8中“空调温度设定值”中的值分别设置。不同档位除了室内温度设定值外,模拟中的其他参数设置情况完全相同。图4为30个房间用户分别在不同档位控制下PMV的平均值变化情况。只考虑每天办公时段8:30-17:30的PMV值,其余时段的值不考虑。规定|PMV|>0.5 的时间为用户不满意时间,4个档位下的用户不满意时间见表8中“用户不满意时长”。

表7 PMV热感觉标尺

表8 不同控制档位激励套餐
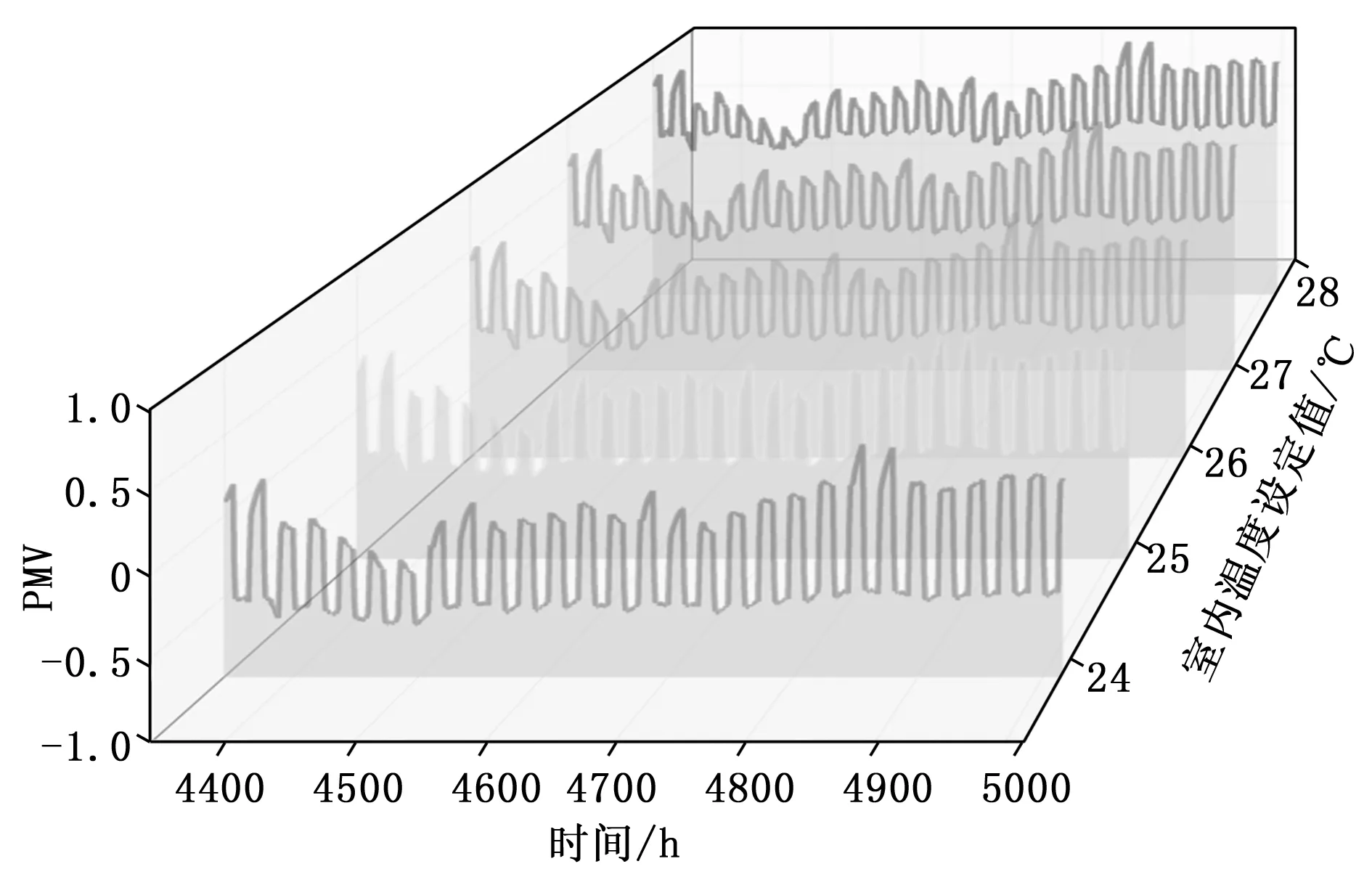
图4 不同控制档位下用户PMV平均值变化
为了差别衡量不同档位的激励价格,现提出用户不满意百分比(ε%)的概念。ε% 表示的是受控时期用户不满意时间占总受控之间的百分比,如式 (7)所示。不同档位的激励价格通过其各自ε%之间的相对关系来确定,规定档位Ⅰ的激励费用为0.2元/kW·h,根据式 (8)可得出相应控制档位的激励费用如表8所示:
(7)
(8)
式中,Tno表示用户不满意时间,Tto表示控制总时间;Ci和Cj分别表示第i、j档位的激励电价;εi%和εj%分别表示第i、j档位的用户不满意百分比。
2.2 功率调控目标值确定
选取典型年7月20日~7月22日连续三天作为需求响应日,办公楼的工作时间08:30-17:30作为空调参与调控时段。图5为调控期间室外气象参数情况。利用1.3节建立的VRV功耗数学模型,通过仿真计算得出未调控之前空调各时段的功率值,假定对办公建筑工作时间的各个时段均实行功率削减,目标调控功率和原始功率的关系如下:

图5 调控期间室外干球温度和相对湿度变化
PDR,t=PAC,t·(1-η)
(9)
式中,PAC,t为未调控之前t时段的平均功率,PDR,t为t时段的功率目标调控值;η为功率削减百分比,为测试在不同功率调控目标下的调控效果,分别取5%、10% 和 15% 三个值。
由式(9)得出VRV空调在需求响应期间各时段的功率目标调控值,各时段的原始功率与目标功率值如表9所示。
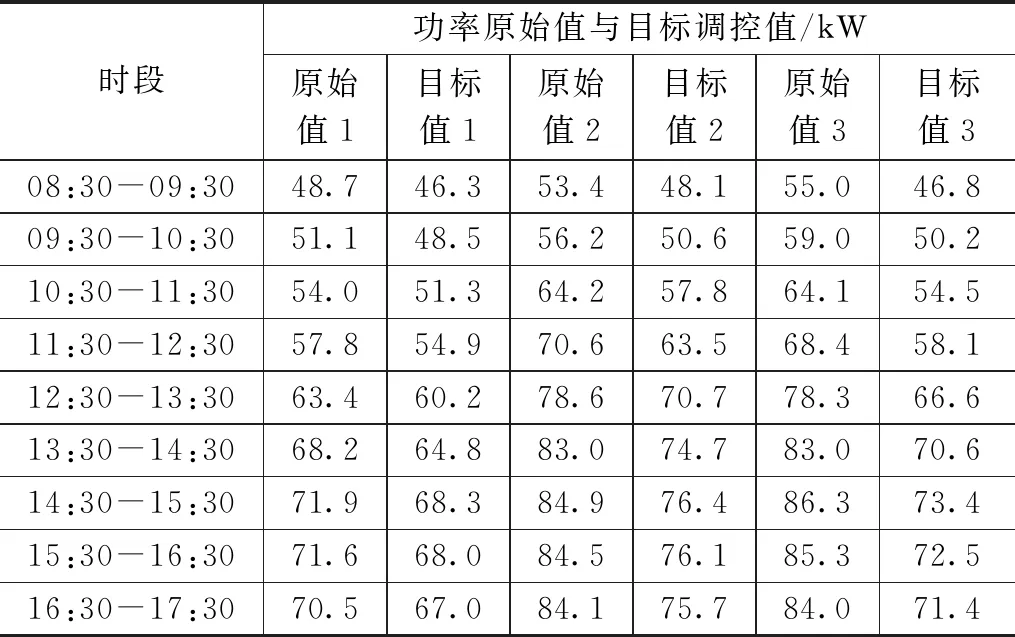
表9 各时段功率原始值与目标值
2.3 目标函数
需求响应手段的实施效果,是在调控策略的制定中需要着重关注的一个方面,其关键的一点就是用户侧实际功率响应目标功率的精度。功率控制精度越高,即实际功率与目标功率的差值越小,就说明了用户侧对电网调控指令的响应效果越好,就更加有利于电网的稳定高效运行。为了反应实际功率与目标调控功率之间的偏差,使用参数误差(PE,parameter error)和平均参数误差(APE,average parameter error)两个指标来表示调控的误差大小,如式 (10)和(11)所示。为了准确响应电网在需求响应期间各个时段的功率削减指令,现要求需求响应期间调控的平均参数误差最小,如式 (12)所示:
(10)
(11)
F1=minAPE
(12)
式中,P*DR,t为空调系统在调控期间第t个时段的实际消耗功率,PDR,t为t时段的功率目标调控值;n为时段数。
2)考虑负荷聚合商的经济效益,在满足调控目标的同时,要求需求响应期间其对用户的激励补偿费用最小。如式(11)所示:
(13)
式中,Ej为空调受控于各档位产生的电量,Cj为各档位的激励价格,j代表控制档位编号。
优化过程中,需要平衡不同优化目标对结果的影响,本文采用加权求和的方法将上述多目标优化模型转化为单目标问题进行求解,由于不同目标的量纲不同,因此需要对各个目标函数进行归一化处理,得出最终的优化模型为:
(14)
式中,F1、F2分别代表优化过程中当前功率偏差、激励成本,F1,max、F1,min、F2,max、F2,min分别代表历史寻优过程中功率调控平均误差、激励费用的最大值和最小值;Ti代表室内机设定温度,t代表控制时段,i代表室内机编号;λ1和λ2为权重系数,本次优化认为目标二者具有相同权重,即λ1=λ2=0.5 。
2.4 约束条件
为保证空调参与需求响应调控的效果,以及机组的正常运行并且不对用户使用空调造成过多的影响,制定如下约束条件:
1)所有时段调控的平均参数误差应控制在5%以内,即
APE≤5%
(15)
2)各室内机设定温度控制在24~28 ℃之间。
3)根据生产厂家对机组的性能要求,空调机组的部分负荷率PLR 不能低于30%,否则压缩机持续在低负荷情况下运转会出现停机等问题。
4)为了避免因频繁操作对用户造成太大影响,现规定每台室内机在需求响应期间所能够接受的最大控制次数为5次,受控于同一档位的次数最多不超过2次,并且每个时段参与调控的室内机数量不得超过室内机总数的2/3。
3 改进人工蜂鸟算法
3.1 算法原理
人工蜂鸟算法的灵感来源于自然界中蜂鸟的觅食行为,其在执行优化过程中模拟了3种觅食行为,包括引导觅食、区域觅食和迁徙觅食。同时,在觅食行为中模拟了轴向、对角和全方位3种飞行技能。此外,还使用访问表来模拟蜂鸟选择食物来源的记忆能力。访问表跟踪每只蜂鸟对每个食物来源的访问程度,访问表中的值越高,意味着该食物来源为蜂鸟积累了更多的花蜜量,将促使蜂鸟优先访问该食物来源。同时,在每个不同的觅食阶段,访问表都会根据候选解的质量进行更新。AHA首先随机初始化一组解和访问表。在每次迭代中,蜂鸟可以通过引导觅食向其预期的食物来源迁移,区域觅食使蜂鸟能够很容易地移动到自己的邻近地区以寻找新的食物来源,进行引导觅食和区域觅食的概率各为50%。每两次迭代则执行一次迁移觅食,直到达到停止规则。最后,返回花蜜补充率最高的食物源作为全局最优值。以下为算法在执行优化过程中的具体流程步骤。
3.1.1 初始化
随机给定n个食物来源,按如下方式随机初始化蜂鸟种群:
xi=Lb+r·(Ub-Lb),i=1,2,…,n
(16)
其中:Ub和Lb分别是d维变量的上、下边界,r是[0,1]中的随机向量,xi表示第i个食物来源的位置,即给定问题的解。食物来源访问表初始化如下:
(17)
其中:对于“i=j,VTi,j=null”,表示蜂鸟i正处在食物来源j处进食;对于“i≠j,VTi,j=0,”表示食物源j在当前迭代中被蜂鸟i已访问过。
3.1.2 蜂鸟觅食方式
1)引导觅食:在引导觅食阶段,蜂鸟为了获得更多的花蜜量,会倾向于在相同访问级别的食物源中选择花蜜补充率最高的食物源进行访问。在觅食过程中,方向切换向量的引入用来描述全向、对角和轴向3种飞行技能。3种飞行技能的数学模型分别描述如下:
(1)轴向飞行:蜂鸟可以沿着搜索空间中的任何坐标轴飞行,其数学表达式为:
(18)
其中:randi([1,d])表示生成从1到d的随机整数。
(2)对角飞行:蜂鸟可以从矩形的一个角飞到搜索空间的另一个角,其数学表达式为:
(19)
其中:randperm(k)表示创建从1~k的整数的随机排列,r1是(0,1]中的随机数。
(3)全方位飞行:蜂鸟可以朝搜索空间中每个坐标轴投影的方向飞行。其数学表达式为:
(20)
借助以上3种飞行方式,蜂鸟可以对目标食物源进行访问并且获得候选食物源。引导觅食候选食物源的位置更新数学描述如下:
vi(t+1)=xi,tar(t)+D·a·(xi(t)-xi,tar(t))
(21)
其中:Xi(t)是第i只蜂鸟在时间t所处的食物源位置,Xi,tar(t)为第i只蜂鸟打算访问的目标食物源在时间t的位置,vi(t+1)是蜂鸟新的食物来源位置,即新的候选解。a为引导因子,服从标准正态分布N(0,1)。
2)区域觅食:在区域觅食阶段,蜂鸟倾向于在自己的领地内进行局部搜索,而不是访问其他现有的食物来源。当蜂鸟在其区域内进行局部搜索时,会产生新的食物来源作为候选解。区域觅食的数学模型如下:
vi(t+1)=xi(t)+D·b·xi(t)
(22)
其中:b为区域因子,服从标准正态分布。
当在引导觅食和区域觅食阶段产生候选解决方案后,要进行解决方案的更新。将当前与候选食物源位置的花蜜补充率即适应度值进行比较,从而进行食物源位置的更新,第i个食物源的位置更新如下:
(23)
其中:f(·)表示函数适应度值。
3)迁徙觅食:当蜂鸟所在的某个地方的花蜜补充率很差时,蜂鸟往往会迁徙到远离当前区域的地方觅食。在AHA算法中,定义了迁移系数。如果迭代次数超过迁移系数的预定值,则位于花蜜补充率最差的食物源处的蜂鸟将迁移到整个搜索空间中随机产生的新食物源。此时,这只蜂鸟将放弃旧的来源,留在新的来源觅食,随后更新访问表。蜂鸟迁徙觅食的数学模型如下:
xwor(t+1)=Lb+r·(Ub-Lb)
(24)
其中:xwor是种群中花蜜补充率最差的食物来源,r是[0,1]中的随机数,Ub和Lb分别为搜索空间的上、下边界。
3.2 改进AHA算法
3.2.1 Hammersley序列初始化种群
人工蜂鸟算法的初始种群是在搜索空间中随机生成的,因此无法确保种群的均匀分布以及产生重复个体的可能性,从而会降低算法的收敛速度和精度。针对AHA随机产生的初始种群分布不均匀的问题,采用Hammersley序列来生成初始种群,该序列可以在高维空间中随机生成均匀分布的种群并且避免种群个体产生重复,从而提高初始种群的质量[23]。Hammersley序列是将任意一个整数表示成以素数p为数位的多项式求和的形式,并将各数位的系数进行反向排序放置在小数点后,从而组成以素数p为基数的小数。Hammersley序列生成的具体步骤如下:
1)对于任意自然数n,都能表示成以素数p为基数的多项式,其中,ai∈[0,p-1]。
(25)
2)将以基数p生成的表达式的系数am,…,a1,a0进行反向排列,并在前面加上小数点,求取 :
Φp(n)=(0.a0a1…am)p=a0p-1+a1p-2+…amp-m-1
(26)
3)n的维度为d,则生成的d维空间 Hammersley序列如下:
(27)
其中:p1,…,pd-1是根据维度确定的素数,N为样本集中点的个数。
将搜索范围划分为两个跨度相同的子空间,两个子空间分别按照式(28)和(29)生成N个H序列,然后计算2N个种群位置对应的适应度值,选取前N个较优的种群位置作为初始位置。
s(i,:)=Lb+(Mb-Lb)*H(i,:)
(28)
s(i+j,:)=Mb+(Ub-Mb)*H(i,:)
(29)
其中:Ub为变量的最大值,Lb为变量的最小值,Mb为变量的中间值。
因此,初始化种群蜂鸟种群的步骤为:
Step1:规定种群规模为N,维度为D,搜索范围为[Lb,Ub];
Step2:将搜索范围划分为两个相等的子范围 [Lb,Mb]和 [Mb,Ub];
Step3:根据维度D来确定素数向量 ,根据Hammersley序列生成N个蜂鸟食物源位置,并按照映射规则映射到相应区间内;
Step4:将2N个蜂鸟种群位置的适应度值进行排序,选取最优的N个作为初始蜂鸟食物源位置。
3.2.2 高斯时变策略
为了进一步平衡并提高算法的局部勘探与全局搜索能力,提出一种基于时变高斯变异的蜂鸟食物源位置扰动策略,在蜂鸟的觅食搜索阶段,采用时变高斯变异算子对蜂鸟食物源的位置进行扰动,即
(30)
其中:为更新后的蜂鸟食物源的位置,为原始的蜂鸟食物源位置;G(0,1)是满足高斯分布的随机变量;γ为时变参数,随着迭代次数的改变而变化;t当前迭代次数,T最大迭代次数。
在寻优初期,由于此时γ值较大,因此有着较大的变异尺度,有利于算法进行全局搜索并且及时跳出局部最优。在寻优后期,由于算法此时基本已达到收敛,因此γ值较小,变异尺度较小,只对蜂鸟食物源位置进行细微扰动,有利于算法的局部开发。得到通过扰动后的新食物源位置以后,计算新位置的适应度函数值,再通过与原始食物源位置的适应度值进行比较决定是否进行解的更新。
3.3 HAGSAHA求解步骤
应用HAGSAHA求解时,以所有时段功率调控偏差平均值以及激励费用同时最低作为蜂鸟食物源适应度函数,将各台室内机在调控期间的温度设定值作为优化变量,以空调机组工作特性和用户用电需求为约束条件。其求解流程如图6所示,算法具体求解步骤如下:

图6 MOAHA算法求解流程图
步骤1:按3.2.1节方式初始化参数,包括种群大小及位置、最大迭代次数和访问表;
步骤2:基于式(14)计算各个食物源的适应度值;并保存目前最佳食物源位置Xbest;
步骤3:利用式(21)执行引导觅食,并按式(23)更新候选食物源位置;
步骤4:利用式(22)执行区域觅食,并按式(23)更新候选食物源位置;
步骤5:利用式(24)执行迁徙觅食 ;
步骤6:利用式(30)对食物源位置进行扰动,重新计算适应度值并更新食物源位置,比较并保存当前最佳食物源位置Xbest;
步骤7:判断是否符合停止标准,若不符合,返回步骤3,否则输出优化结果。
4 实验与结果分析
4.1 算法参数设置
为了测试改进后算法的优化性能,选取PSO、GWO、WOA这3种成熟的智能优化算法以及改进前的AHA与HAGSAHA作为对比共同对模型进行求解。5种算法的相关参数设置见表10。4种算法代码的编写、调试和运行均在Matlab 2019b中进行。每个算法在求解过程中各运行20次,取运行结果的平均值作为优化结果。

表10 算法参数设置情况
4.2 优化结果分析
图7为采用不同算法的功率调控误差结果对比,由图中可看出,无论功率削减百分比为多少,所有算法的控制偏差均在5%以内,满足控制精度要求。此外,HAGSAHA总体上较其他4种算法均表现出了较低的相对误差,在3种功率削减指令下与目标功率的平均相对误差分别为:0.41%、1.07%、0.93%,如表11所示。

表11 调控结果平均相对误差 %

图7 不同算法功率调控误差结果对比
表12为使用不同算法计算出的需求响应期间应支付给用户的激励补偿费用情况,由此可以看出随着功率削减百分比的增加,激励费用呈上升趋势。其中,HAGSAHA除了在功率削减百分比为5% 时略高于 AHA的优化结果,在其余两种调控指令下的激励费用均为所有算法中的最低。HAGSAHA在3种调控指令下的平均激励费用为243.2元。
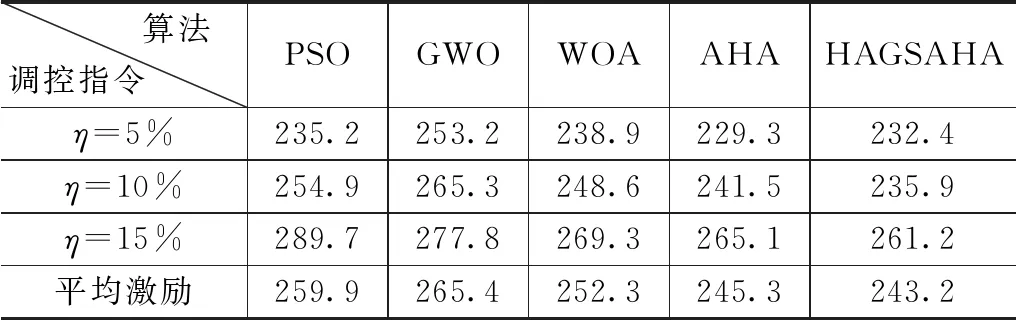
表12 不同算法激励费用对比 元
由此可看出,采用HAGSAHA优化求解后的功率调控精度与激励费用均优于其他4种算法。相比其他算法,HAGSAHA在3种功率削减指令下的调控精度最高分别提升了83.1%、54.3%和66.3%,平均激励费用最多减少了8.36%,在调控偏差与激励费用两个方面的优化结果上同时取得最优,实现了需求响应调控目标,达到了较好的优化效果。
4.3 室内机受控情况
图8为采用HAGSAHA优化后不同功率削减百分比下各时段的室内机受控情况,由此可看出随着功率削减百分比的增大,参与调控的室内机数量也在变多。其中,各时段受控于低档位(Ⅰ、Ⅱ档)的室内机数量占比总体呈下降趋势,受控于高档位(Ⅲ、Ⅳ档)的室内机数量占比总体呈上升趋势。这是因为,制冷工况下,空调功耗一般是随着设定温度的升高而降低,功率削减百分比越大即空调实际运行功耗越低,在参与调控的用户数量有限制的情况下,设定温度高的室内机数量也就越多。且各时段参与调控的室内机数量均在20台以内,满足调控要求。
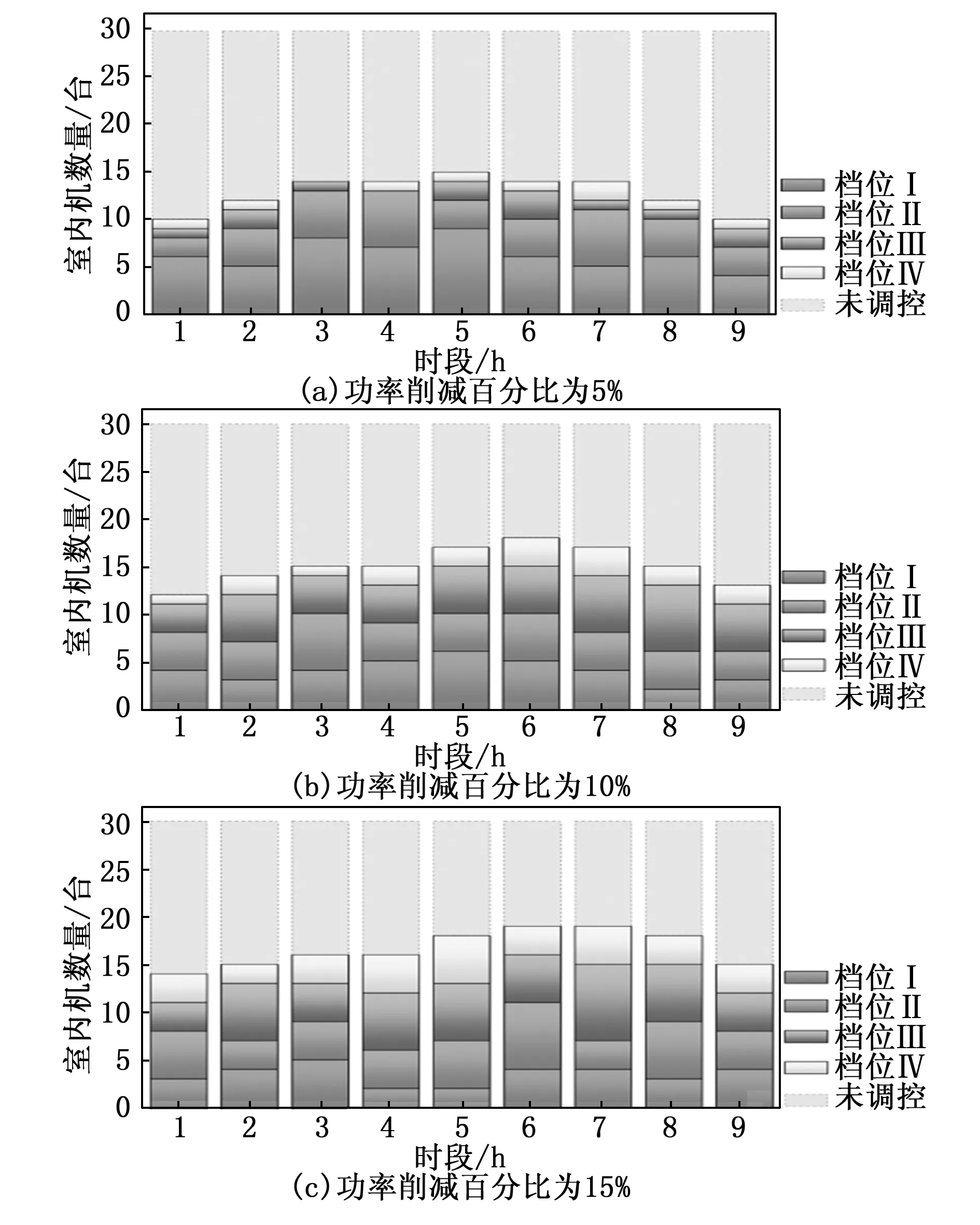
图8 调控期间各时段室内机受控情况
4.4 用户舒适度分析
在满足调控目标的同时,调控期间各个房间人员的舒适度也是值得关注的一方面。我国对于空调室内舒适性的要求可以参考《中等环境 PMV 和 PPD 指数的测定及热舒适条件的规定》[24](GB/T 18049-2000)中的相关规定,该标准指出,空调房间的舒适性在采用在 PMV指标评价时应符合的条件为:-1≤PMV≤1。
为了分析用户在需求响应中的舒适度变化情况,在EnergyPlus中进行调控期间建筑空调用户的热舒适模拟。分别对每台室内机在各个时段的设定温度按4.3节优化结果进行设置,空调参数与人员舒适度的设置见1.2节。图9为所有房间用户在各个时段PMV值模拟结果的统计分布。从图中可以看出,在3种功率削减百分比下,所有房间用户的PMV均值分别为-0.202,0.198和0.581。随着功率削减百分比的增加,用户PMV值有所升高,除了在功率削减百分比为15%下有大于1的情况出现,其他时候PMV值均在 [-1,1]内,满足调控期间用户对于舒适度的要求。
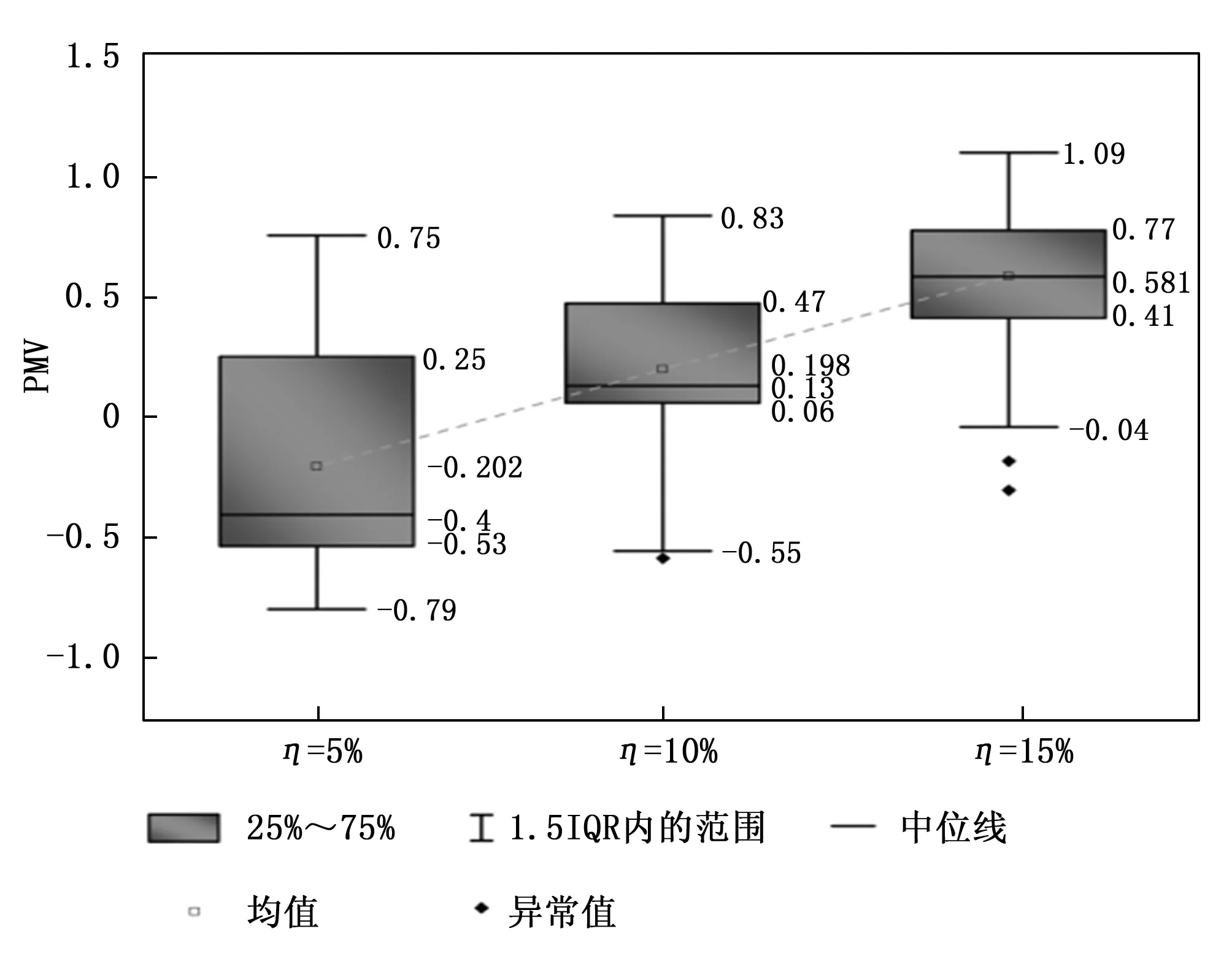
图9 不同功率削减百分比下调控期间PMV统计分布
4.5 算法性能对比
为了验证改进后算法的优化性能,分别绘制出5种算法运行20次的平均收敛曲线如图10所示,由图可以看出,虽然传统的PSO算法在迭代次数达到50次左右就达到收敛,但是寻优的精度很低,整体优化效果不是很好;GWO、WOA和AHA算法相比于PSO算法,在优化精度方面有一定的提升,但容易陷入局部最优解,收敛结果仍然不是全局最优解;而改进后的HAGSAHA算法,在第70次左右就达到了收敛,相比于改进之前的AHA算法在收敛速度以及优化精度上都得到了提升,这是由于使用Hammersley序列均匀化初始种群使得搜索效率得到了增强,也进一步提高了优化精度。而在搜索阶段高斯变异算子的扰动下又进一步增强了算法的搜索能力,同时能有效避免陷入局部最优的不足。相比之下,改进后的人工蜂鸟优化算法无论是在收敛速度还是求解精度方面都得到了较大的改善。由此可以看出,所提出的HAGSAHA算法可以有效地应用于办公建筑VRV空调需求响应优化调控策略的制定中。
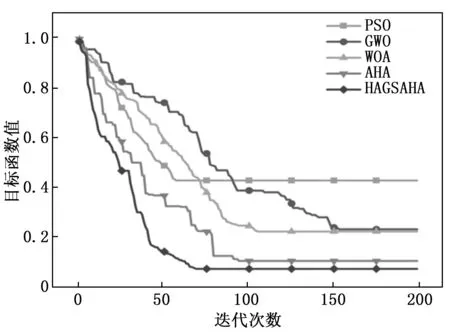
图10 不同算法的平均收敛曲线
5 结束语
针对夏季用电高峰用户对空调设定温度的随意调节影响电网运行安全以及用户侧对电网调控指令响应不够精确的问题,以某办公建筑VRV空调系统为研究对象,提出基于不同舒适度和激励电价的温度分档控制方案,基于功率削减指令构建室内机温度分档优化调控模型,运用所提出的HAGSAHA算法对模型进行求解,得出结论如下:
1)随着功率削减百分比的增大,参与调控的室内机数量也随之增多,其中各时段受控于Ⅰ、Ⅱ档位的室内机数量占比总体呈下降趋势,受控于Ⅲ、Ⅳ档位的室内机数量占比总体呈上升趋势。
2)应用HAGSAHA求解出的3种功率削减指令下功率调控值与目标值的平均相对误差分别为0.41%、1.07%和0.93%,平均激励费用为243.2元,同时保证了调控期间用户的舒适度处在舒适范围内。
3)在3种功率削减百分比下HAGSAHA相比其他3种算法的功率控制精度最高分别提升了83.1%、54.3%和66.3%,平均激励费用最多减少了8.36%,体现出HAGSAHA在求解实际工程问题上较好的优化性能。
