不同含水率条件下树木内部应力波传播规律的研究
2023-10-27鲍宇杜晓晨叶程浩
鲍宇,杜晓晨,2,叶程浩
(1. 浙江农林大学 数学与计算机科学学院,浙江 杭州 311300;2. 林业感知技术与智能装备国家林业和草原局重点实验室,浙江 杭州 311300 )
为了检测树木缺陷、评估树木质量,应力波、超声波、X 射线和CT 等工具和方法被应用于树木检测领域[1-4],其中应力波检测技术因为较为便捷的检测方式和较为准确的检测结果被广泛采用[5-6]。应力波检测主要基于树木中应力波传播速度、树木密度和树木弹性模量之间的关系[7-8]。而树木具有吸湿性、异质性和各向异性,所以应力波在树木中的传播会受到含水率和温度等因素的影响[9]。Gray 等研究了含水率和温度对应力波在红松Pinuskoraiensis树木中传播速度的影响,实验证明含水率和温度是影响树木中波速的重要因素[10]。刘昊等研究认为当水分含量低于纤维饱和点时,波速变化幅度更为显著[11]。Toyoshima 等经过大约半年的木材自然干燥实验,研究了树木从生材状态到接近纤维饱和点的过程中应力波速度的变化和木材纤维饱和点的关系[12]。Xu 等研究了含水率高于50%时应力波速度不会随着温度的降低而线性增加,而是在接近0 ℃时突然跳跃的现象,树木中的所有自由水和小部分结合水都由水转变为冰,从而影响了树木的物理性能[13]。徐华东等采用红松试件进行测量实验,深入分析了树木内波速在不同含水率水平下的变化规律[14]。
近年来,国内外对树木内部应力波的传播规律进行了许多深入研究。Teodorescu 等的研究表明树木中水的存在是影响树木机械性能的重要因素,并且会随着气候和季节的变化而改变[15]。翁翔等研究应力波在树木内部径切面上的传播规律及影响因素,建立了传播速度模型[16]。Wei 等研究了应力波在不同含水率下的三维空间中的传播速度,得到了不同空间角度下应力波传播速度的理论模型,以及含水率对树木物理力学性能的影响[17]。但目前并未有在树木检测实际应用场景,即在活树中进行含水率等因素对应力波在树木内部传播速度影响的研究。为此,本研究旨在分析不同含水率下树木内部空间应力波的传播速度,以期更为明确地探究应力波在树木内部的影响因素和传播规律,建立含水率的应力波传播速度的回归模型,为树木缺陷检测技术提供理论依据。
1 应力波在树木内部的传播过程理论
1.1 应力波在树木横切面中的传播理论分析
首先,将树身视为理想的圆柱形,然后建立如图1 所示以O为原点的三维坐标系,此中x轴、y轴、z轴分别代表径向、切向和纵向,则x-y平面代表横切面,x-z平面代表径切面。假设应力波由O点发出向S方向传播,则以α表示应力波传播方向与树木纤维方向之间的夹角,θ表示径向与应力波传播方向之间的夹角。在横切面与径切面中则分别以r和β来表示应力波传播方向与对应切面的夹角。

图1 树木坐标系统示意图Fig. 1 Tree coordinate system
Hankinson 公式对应力波在树木纤维中的强度和传播速度与树木纤维角度的关系进行了研究[18]。当应力波在树木的径切面中传播,设应力波的传播方向和树木纤维夹角为β,则可得出波速[v(β)]的计算公式如下:
张春晓等在Hankinson 研究成果的基础上,对应力波在树木纤维中的强度和传播速度与树木纤维角度的关系进行了研究,得出应力波在树木径切面中的传播速度与纵截面夹角之间的联系[19],即树木径切面中波速(v)与弦向角(r)关系的公式:
式中,ER、GRT分别为树木径向弹性模量、切向弹性模量以及树木剪切模量,数值大小固定不变。由上式可知,应力波在树木横切面中传播时,波速v与传播方向角r间的曲线可近似视为二次曲线,开口向下且当r=0 时对称。
树木的含水率对在其中传播的应力波频谱有着较为显著的影响,应力波频谱中的共振频率表现出由含水率水平的上升而降低的趋势,当树木中的含水率低于其纤维饱和点的时候,其中传播的应力波频谱共振频率受含水率的影响更为显著,所以应力波在树木中的传播速度大小随含水率的减小呈逐渐上升的趋势[20]。
不同树种的树木密度、纤维质地等属性存在差异性,这些属性也会显著地影响树木内部的应力波传播速度大小[21]。所以将含水率(mc)与树种性能系数(T)引入理论模型中,可得到下式:
1.2 应力波在树木径切面中的传播理论分析
刘光林等得出应力波在树木径切面中传播的速度与其传播方向和径切面的夹角大小相关,设树木中应力波传播方向角为θ,应力波与径切面夹角为α[22],则可得下式:
式中,vl为应力波在树木纵向传播的速度,vR为应力波在树木径向传播的速度。同样在径切面的波速公式中也引入含水率(mc)与树种性能系数(T),则可得:
1.3 应力波在树木内部空间的统一传播理论分析
通过以上树木横切面与径切面的应力波传播理论分析可以发现,应力波在两个切面上的传播速度公式化简后具有相同的形式。所以在此可以将树木内两个切面独立的模型合并统一为树木内部空间中的理论模型。化简后的应力波在树木内部传播的速度公式可以表示为:
式中,y为应力波在树木中的传播速度,x为应力波传播所在切面中传播角度与切面的夹角角度。k是树木内应力波传播速度系数,大小由树木弹性模量及应力波传播所在切面决定。由上式可得出应力波在树木内部空间中的速度公式为二次曲线型,曲线最大值即传播速度的最大值由应力波传播角度、树种和含水率决定。
2 材料与方法
2.1 研究区概况
选择浙江农林大学植物园作为试验基地,该基地位于浙江省杭州市临安区(30°23′ N,119°72′ E),在亚热带季风气候区南缘,年平均降水量约为1 600 mm,年降水日约为150 d。光照条件良好,四季分明。基地内主要分布有樟Cinnamomumcamphora、鹅掌楸Liriodendronchinense、乐昌含笑Micheliachapensis、响叶杨Populusadenopoda等树木。选择其中具有代表性的樟样木及其树木圆盘作为研究对象,樟样本树龄25 年,树木圆盘选取基地内相同树龄的樟进行采样,采样部位位于树干距离地面1.3 m 处。
2.2 实验设备
测量应力波传播速度使用浙江农林大学自主研发的林木缺陷检测仪,这套仪器配套应力波传感器和PC 端的缺陷二维成像程序。林木应力波缺陷检测仪的测量原理是计量应力波在树木各点之间传播的距离和时间,最终计算出速度矩阵并生成内部缺陷的二维图像。树木含水率的测量采用KT-R 撞锤针插式树木湿度仪,测量树木含水率范围为0 ~ 100%。树木圆盘样本烘干和温湿度控制采用济南奥迈电子设备有限公司AM-HG60 型电热鼓风烘箱,利用循环风机鼓风干燥,维持控制内部的湿度和温度范围。主要设备如图2 所示。

图2 树木应力波检测设备Fig. 2 Tree stress wave tester
2.3 实验方法
2.3.1 波速测量 在待测量树木各个应力波传感器部署点上依次设置好传感器,图3A 和图3B 分别为树木横切面和树木径切面波速测量中传感器的设置示意图,箭头指向代表各个编号应力波传感器的部署方位。发出应力波后测量应力波在树木中传播到每个接收端所用的时间,再结合每个传感器之间的间距便可以得出应力波在树木中传播的速率。测量树木横切面中的应力波传播速度时分别将每个传感器都依次视为坐标系原点,并将十二个应力波传感器的波速数据求平均值以减小误差。而在测量树木径切面中的波速时同样分别以每个传感器为原点,以不同的传感器为原点可以测量到不同应力波传播角度的波速数据,综合一侧的六个传感器可以得到应力波在树木径切面上完整传播角度范围的数据,然后两侧数据取平均值以减小误差。波速测量完成后,使用Origin 和SPSS 程序开展数据分析与制图。

图3 传感器部署方案Fig. 3 Distribution of sensors
2.3.2 含水率控制与测量 在每次波速测量时测量并记录对应的含水率,本研究实验样本分为活树样本和树木圆盘样本,测量活树含水率和温度采用KT-R 插针式木材湿度仪可以实时快捷读取数据。测量树木圆盘样本含水率则采用烘干法,参照现行木材含水率测定方法国家标准,对所要测量的样本展开初始的质量记录,然后将树木圆盘样本放入水中浸泡,经过一段时间后测量其质量以计算当前含水率,然后实验记录当前含水率下的树木内部的波速。完成一次测量后继续将样本放入水中浸泡,按照上述方法循环多次测量,在整个实验过程中共记录6 次含水率及相应的应力波传播速度。
3 结果与分析
3.1 不同含水率下树木横切面波速分析
将采集到的数据导入Origin 软件绘制得到树木内部波速的散点图,再经过曲线拟合之后可以得到不同条件下的波速曲线图。樟样本和圆盘样本在不同含水率下树木内部横切面的波速变化如图4 和图5 所示。拟合后的曲线呈现出开口向下且以0°方向角对称的抛物线。在树木内部横切面中,应力波的速度随传播方向角度的增大而减缓,在传播角度等于0°时应力波传播的速度最快。当树木中具有不同含水率的时候,方向角对树木横切面中应力波的速率有着较为相似的影响。同时,树木中的应力波速率随着含水率的升高而下降。在图5B 中,树木的含水率到达30%时,应力波速度变化较大,此时木材纤维达到饱和点,树木内部的物理力学性质将产生变化。当含水率大于这个点的时候,应力波的速度随含水率升高而变化的幅度较小,而当树木含水率小于这个点时,树木中应力波的速率随含水率变化的幅度较大。
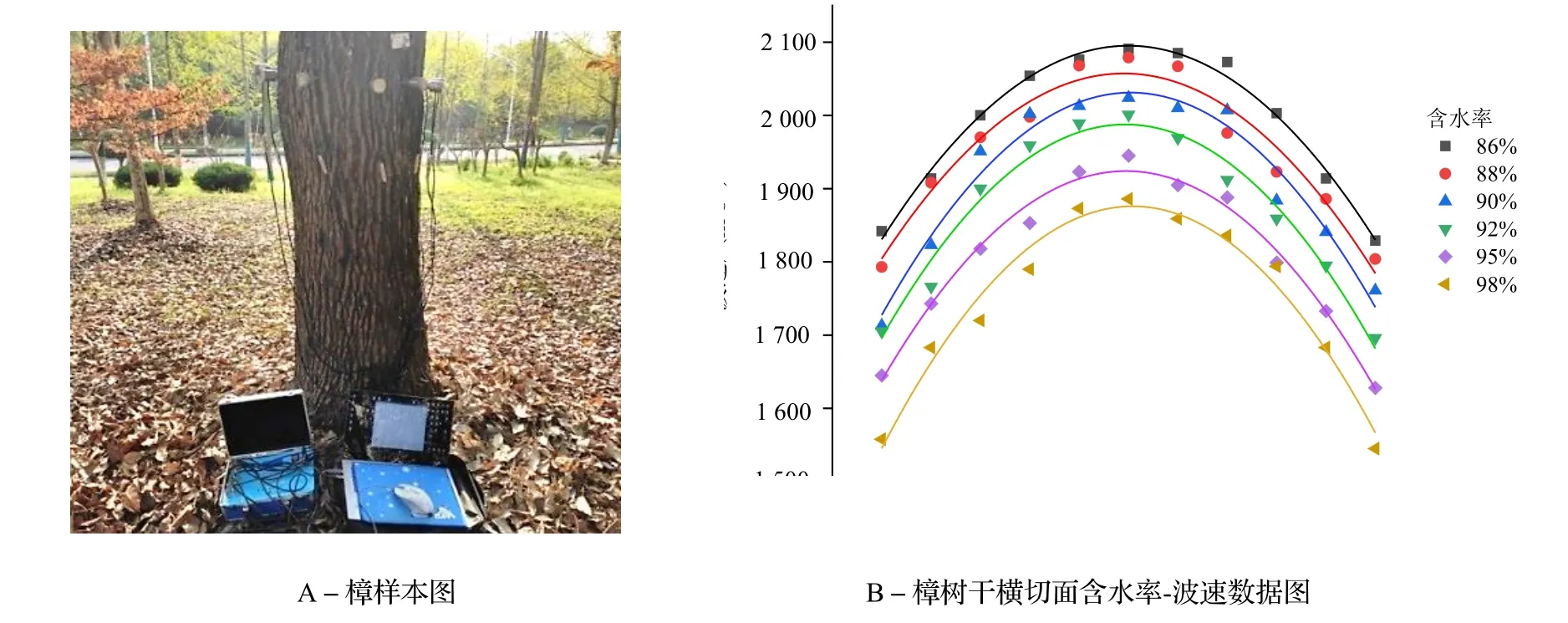
图4 在不同含水率下樟树干横切面中的波速Fig. 4 The wave velocity in radial section of living camphor tree under different moisture content

图5 在不同含水率下樟圆盘样本横切面中的波速Fig. 5 The wave velocity in the radial section of disc camphor sample under different moisture content
采用Origin 软件根据数学模型 y=1+kx2+mc·T 对应力波速度和方向角数据进行回归分析,并建立它们之间的回归模型(表1)。

表1 横切面中不同含水率的波速与方向角的回归分析Tab. 1 Regression analysis of wave velocity and angle of different moisture content in cross section
实验样本的所有树木含水率,应力波传播速度与方向角的回归曲线均满足模型函数,决定系数(R2)均在0.94 以上,表明该模型有着比较良好的相关性。除樟外,其他几个受测树种也都得到了相似的结果。可以得出,在不同树种内部横切面中,含水率对波速的影响都是相同的,即树木的含水率越高,在树木内部横切面中波速越慢,且当含水率在树木的纤维饱和点以下时此规律更为明显。
3.2 不同含水率下树木径切面波速分析
径切面的波速分析的活立木样本与上文横切面分析为同一株樟,树木长段样本则另外选取合适长度的樟树干长段。将不同含水率条件下的树木内部应力波的速率数据绘图拟合后如图6 和图7 所示。拟合后的抛物线以0°方向角为对称轴,开口向上,从图中可以得知树木内部径切面中的应力波速率随着方向角的增大而提升,当传播方向为径向时树木内波速到达最大值。与横切面相同的是在不同含水率时,方向角变化对径切面中应力波速率的影响同样有着相似性,并且波速同样随着含水率的升高逐渐下降,在木材纤维饱和点以下时应力传播速率受含水率的影响更大。但是应力波在树木径切面中的传播速度受含水率影响并没有在横切面中受到的影响显著,即波速随含水率变化的幅度更小。
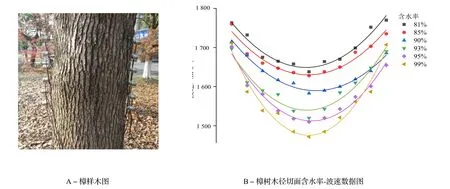
图6 在不同含水率下樟树木样本径切面中的波速Fig. 6 The wave velocity in radial section of the living camphor tree under different moisture content

图7 在不同含水率下樟树木长段样本径切面中的波速Fig. 7 Wave velocity in radial section of long tree samples under different moisture content
对应力波速度和方向角数据进行回归分析后建立它们之间的回归模型,结果见表2。由表2 可知,实验样本的所有含水率、应力波速度与传播角度的回归曲线均满足模型函数,决定系数(R2)均高于0.93,可看出模型的相关性较好。其他不同受测树种的样本数据也满足该模型。这表明在不同树种内部径切面中,含水率对波速的影响都是相同的,即含水率越高,波速越慢。且含水率在木材纤维饱和点以下时此规律更为明显。当树木含水率大于50%时,由于树木内部的自由水占比增大,不同传播角度上应力波的传播速度降低且变化幅度减小。
4 结论与讨论
为了给树木无损检测与成像技术提供更准确的理论依据,实现提高树木资源利用率的目标,国内外专家学者做了许多研究,在研究树木中应力波速度的影响因素和建立树木中应力波的传播速度模型等方面获得了许多成果。本研究旨在分析不同含水率下树木内部空间应力波的传播速度,以期在前人研究的基础上更为明确地探究应力波在树木内部的影响因素和传播规律,建立关于含水率的应力波传播速度的回归模型,为树木缺陷检测技术提供理论依据。
前人分别提出了树木横切面和径切面的应力波传播速度模型,并通过实验验证了所提出的波速模型的准确性。为了进一步提高模型的准确性,需要考虑影响树木内部应力波传播速度的因素,并将之引入波速模型中。本文通过研究树木内部应力波的传播过程理论与含水率对树木内部应力波传播速率的影响,分别提出了树木横切面和径切面中与含水率相关的波速模型,并将两个波速模型进行了统一。经过实验验证,波速(y)与方向角(x)、含水率(mc)和树种参数(T)满足函数关系y=1+kx2+mc·T,回归模型与实验结果吻合良好(R2≥0.93)。
本研究在前人研究的基础上进一步探究了含水率因素对于树木内部应力波传播速度的具体影响。研究结果表明树木内部应力波速率随着含水率提升逐渐减小,当树木的含水率低于其纤维饱和点,波速受含水率影响更为明显,而当含水率高于树木纤维饱和点,波速减小的趋势逐渐放缓。且本研究发现在树木内部径切面上应力波传播速度随含水率的变化幅度比横切面上的更为显著。
