强激光脉冲中高能电子辐射的时间演化研究

孙诗晨,田友伟,薛洪涛

(1.南京邮电大学 贝尔英才学院,南京 210023;2.南京邮电大学 理学院,南京 210023)

1 引言

近些年来,随着啁啾脉冲放大技术的进一步发展[1-3],激光脉冲的宽度得以被进一步的压缩,峰值功率也随之大幅提高,在适当聚焦后,为激光场达到相对论光强创造了条件。这就为探讨相对论电子动力学的有关问题提供了新途径、新方法,也更加激发了人们对于激光脉冲和粒子相互作用这个领域的研究热情。

在此基础上,对于激光脉冲与粒子相互作用的理论研究有了新的发现和进展。郑君等人对单电子非线性汤姆孙散射的影响因素进行了研究,发现入射激光的强度、偏振态以及电子的初始状态都会对电子的散射和辐射产生重要影响[4];兰鹏飞等人通过研究Thomson 散射辐射的空间分布,得出极角和方位角都显著地依赖于超短脉冲的载波相位η0[5];Wang等人分析了圆偏振激光脉冲非线性汤姆逊散射的空间辐射和运动特性[6-8],发现了强激光脉冲中非线性汤姆逊散射的涡旋与对称辐射特性[9]。

但是,我们目前了解到的关于高能电子辐射的研究并没有涉及其随时间的演化。因此在本文中,我们在前人的研究基础上探讨了激光与电子不同作用时间下的电子辐射能量。通过数据模拟仿真,可以发现二者作用的前1000飞秒内,辐射的空间分布随时间的变化幅度较大,此后辐射集中在中心位置。计算结果还能表明,随着作用时间的增加,电子辐射能量的最大值先增加,后稳定不变,呈现S型增长趋势。这说明,激光与电子作用时间的长短会对应辐射的空间分布和辐射能量大小的不同特征,可以通过合理调整作用时间得到更加理想的辐射效果。

2 电子与激光脉冲作用模型

电子与激光脉冲作用示意图如下所示:

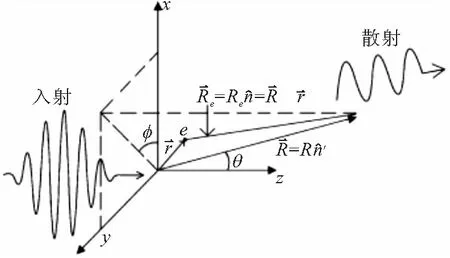
图1 电子与激光脉冲作用示意图

对于圆偏振啁啾高斯脉冲,它的归一化矢式通常表示如下:

(1)

其中,

aL=exp(-η2/L2-ρ2/b2)(b0/b),a0表示被mec2/e归一化的激光峰值振幅,大小为:

(2)

式(2)中,I0表示激光脉冲的光强,λ0表示激光的波长,本文取λ0=1μm处理。

笛卡尔坐标中,高斯圆偏振激光脉冲的相位φ表示如下:

φ=η+φR-φG+φ0

(3)

式(3)中,η=z-t,

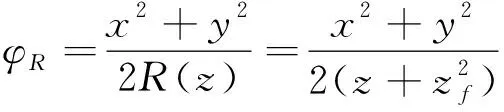
笛卡尔坐标中矢量势的分量如下所示:

ax=aLcosφ,ay=aLsinφ

(4)

(5)

其中θ=π-arctanφG。则辐射方向表示为:

其中θ为极角,φ为方位角,n为从电子与激光的作用点(选定为原点)指向观测点的单位向量,也就是辐射方向。

根据拉格朗日方程和电子的能量方程,电子在电磁波中的运动可以用下面两个公式描述:

dt(p-a)=-∇a(u·a)

(7)

dtγ=u·∂ta

(8)

其中u是用光速c归一化的电子速度,p=γu是标准化动量,γ是相对论因子(也是电子的归一化能量)。

将(4)(5)代入(7)(8)进行运算,可以得到下面的方程组:

(9)

求解这个方程组,就可以得到电子受激光作用影响导致的坐标、速度、加速度以及能量随时间的变化过程。

根据电动力学知识,做相对论加速运动的电子会放出电磁辐射,其单位立体角的辐射能量可以通过(10)计算。

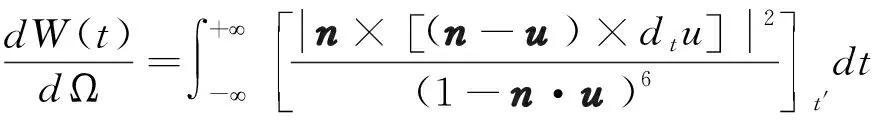
(10)

t=t′+R,R～R0-n·r

(11)

r为电子的位矢,R0是观察点和电子与激光脉冲作用点之间的距离,我们假定观察点远离作用点。

3 数值模拟结果

3.1 辐射能量的空间分布随时间的变化

通过matlab对圆偏振强激光脉冲与高能电子相互作用的过程进行模拟,不断改变激光与电子相互作用的时长,并且计算出相应时间段内单位立体角电子辐射的能量。图2和图3展现了激光与电子不同作用时长下电子辐射能量的空间分布与相应时间内电子的运动轨迹。在此,我们选取的归一化激光振幅为a0=8(I=8.832×1019W/cm2),脉宽L=7λ0,束腰半径b0=3λ0,其中一个波长λ0=1μm对应3.33 fs。

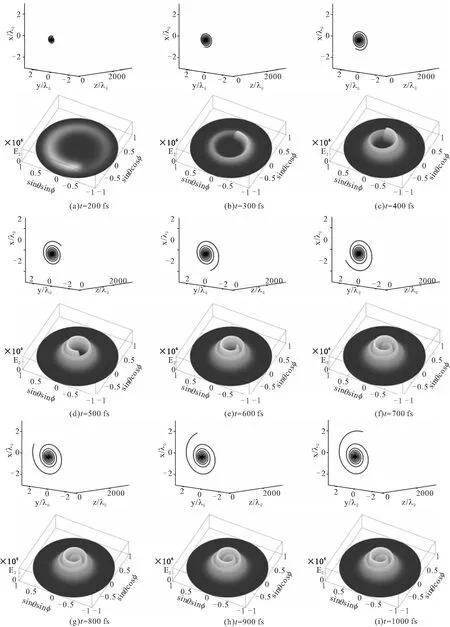
图2 电子运动轨迹和辐射能量分布图像(激光与电子作用时间在200-1000 fs内,每隔100 fs取值)

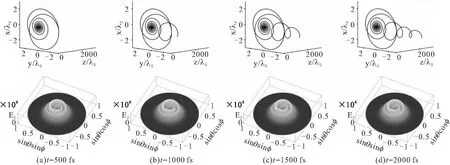
图3 电子运动轨迹和辐射能量分布图像(激光与电子作用时间在5000-10000 fs内,每隔5000 fs取值)

观察图2和图3可以发现,在激光与电子作用的时间段内,电子绕轴做螺旋线运动,轨道半径随时间的推移先增大后减小。并且当t<1000 fs时,其运动主要集中在xoy平面,t>1000 fs后z方向的运动逐渐明显。电子产生的辐射能量则先分布在外沿,且能量较小;随着时间的推移,辐射能量分布逐渐向内集中、形成套圈,呈现出涡旋的形态。从z方向上看,涡旋会先上升到一个最高点,再继续下降,这是因为电子在运动过程中到达了最大能量辐射方向对应的角度(θ,φ),此处的辐射能量就是这段时间内单位立体角的辐射能量dW/dΩ所能达到的最大值。

对比电子运动轨迹和电子辐射能量分布图像,两者随时间变化幅度的快慢有所不同。如图2所示,除去t<100 fs辐射能量太小难以观测的阶段,当作用时间在200～1000 fs内,电子辐射能量的空间分布随时间变化较为明显,且作用时间越短、图像变化越明显;而电子运动轨迹随时间的变化规律恰恰相反:作用时间越长,轨道半径增大的速度越快,且沿z方向运动的速度越来越大,轨迹图像变化也随之愈加显著。当激光与电子的作用时间达到1000飞秒之后,如图3所示,每隔5000飞秒对时间t进行取值,电子辐射能量的分布图像已经看不出变化,这说明在t=1000 fs时电子辐射能量已经集中到中心。此时,电子绕轴运动的轨道半径随时间而逐渐减小,运动速度放缓。

根据以上分析,我们还可以得知,电子辐射能量分布与电子的运动轨迹随时间的变化规律并不相同,这说明电子的运动轨迹大小与电子辐射能量分布并不是同步、同规律随时间变化的。

3.2 辐射能量的最大值随时间的变化

在上述研究过程中,我们还发现,当相互作用时间在1000飞秒内时,随着激光脉冲与电子作用时间的增加,辐射能量涡旋的最高点也有一定的上升趋势。于是,我们计算了不同作用时间下电子辐射能量的最大值,得到电子辐射能量最大值随时间的变化图像如图4所示。

图4 电子辐射能量最大值随时间的变化图像

观察图像可以发现,辐射能量最大值Emax随时间的变化趋势呈S型增长。当t<200 fs,辐射能量非常小。在t=200 fs左右,Emax突然开始增加,直到t=450 fs到达平台期,以极其微弱的趋势继续增长,最后稳定在3.1335×106,即对应归一化前的结果为1.18×10-12J/cm2。此外还注意到t在200～500 fs时间段内曲线的变化幅度先变大后变小,这说明Emax的增大速度先增加后减小,且约t=300 fs时增长速度达到最快。

4 结论

基于单电子在强激光场作用下的非线性汤姆孙散射的经典理论,借助matlab对激光和电子相互作用的过程进行了模拟仿真,细化了强激光脉冲中高能电子辐射随时间的演化过程,得到了激光与电子不同作用时间下电子辐射的空间分布与辐射能量最大值的变化情况。结果表明,在归一化激光振幅a0=8,脉宽L=23.33 fs,束腰半径b=3 μm的圆偏振激光脉冲的作用下,电子辐射能量随时间推移从外向内呈涡旋分布,且在1000飞秒时已经基本集中在中心。同时,随着作用时间越来越长,涡旋向中心集中的变化幅度有递减的趋势,这与电子运动轨迹随时间的变化规律是不同的。此外,电子辐射能量的最大值会受不同作用时间下空间角与最大能量辐射方向间距离偏差的影响,在t=200 fs左右突然增加,且增大速度先快后慢,在t=450 fs到达平台期后继续缓慢增加,直至最终稳定在1.18×10-12J/cm2。