基于改进DE 算法的目标分配问题研究*

李 静，鲁济帅，翟凯玥

（西安工业大学电子信息工程学院，西安 710021）

0 引言

在巡飞弹协同攻击决策中，目标分配是协同战役指挥决策中最重要的问题之一，但其本质仍属于武器分配（weapon target assignment，WTA）问题，WTA是指根据目标威胁、武器和目标的特性等相关约束条件，结合已获得的战场态势信息，对武器和目标进行有效合理分配，从而达到最优攻击效果［1］。

WTA 问题是NP（non-deterministic polynomial）问题，问题求解的难度随目标数量的增大呈指数型增加，而传统的启发式算法，目标规划方法等，难以适应对大规模WTA 问题的求解［2-3］。相比之下，智能算法如PSO 算法［4］、SA 算法［5］、GA 算法［6］和DE算法［7］等，凭借其自身收敛速度较快、寻优性能较强等优点被广泛用于求解此类问题。虽然上述智能算法最终都能得到较为满意的结果，但在求解大规模WTA 问题中，收敛性和寻优能力仍有改进的空间。

DE 算法是基于群体性差异的智能算法，因其鲁棒性好、优化能力强等优点被广泛应用［8］。近几年来，很多研究者借助DE 算法来解决WTA 问题，欧峤等提出一种改进的离散DE 算法，改进了自适应差分变异、随机均匀交叉等操作，提高了求解WTA 问题的时效性［9］；MENG 等提出了一种基于历史种群的突变策略且具有参数自适应机制的DE 算法［10］；徐英杰等提出一种基于小波基函数的差分进化改进算法，通过小波基函数对DE 的缩放因子进行改进，提高了算法性能［11］。

本文提出了一种改进的DE 算法，通过引导“探索性”种群协作进化、自适应选择变异率、变异策略及交叉率来进行改进，然后将改进的DE 算法应用到目标分配模型中进行最优求解，进而提高协同攻击作战决策中目标分配问题的效率。

1 WTA 问题的描述

在某次协同攻击作战中，有m 枚巡飞弹和n 个待攻击目标，对我方巡飞弹和待攻击目标进行分配。假设每枚巡飞弹携带多个武器，可对多个地面目标进行连续打击；假设在巡飞弹集群有效的作用时间和作用区域内，某时刻这m 枚巡飞弹同时到达攻击区域，且某枚巡飞弹在这一时刻可分配多个武器攻击同一目标。则巡飞弹协同攻击目标分配决策矩阵为：

式中，i=1，2，…，m，j=1，2，3，…，n，xij∈（0，mi）（mi为第i 枚巡飞弹的可用武器总数量）；xij=d 为第i 枚巡飞弹分配给第j 个目标d 个武器。

假设同一枚巡飞弹上携带的武器对同一目标的毁伤概率相同，且分配前已获得每枚巡飞弹的武器对攻击目标的毁伤概率，对应的毁伤矩阵如下：

式中，i=1，2，…，m，j=1，2，3，…，n，pij＞0，pij为第i 枚巡飞弹的武器攻击第j 个目标的毁伤概率。

第j 个目标总的毁伤概率可以表示为：

那么毁伤所有目标的数学期望Z 为：

结合战场中敌方目标的综合价值，则可建立目标毁伤综合价值最大的数学模型f（x）为：

其中，vj为第j 个敌方目标的综合价值，目标综合价值vj大小主要取决于目标的综合威胁程度Thi、目标造价Mei和目标任务价值Ati三者的综合加权，具体计算如下：

约束条件1：

该式表示对xij进行整数约束，其值必须为大于等于0 的整数。

约束条件2：

式中，mi表示第i 枚巡飞弹可用武器数量。上式表明某时刻某枚巡飞弹分配给目标的武器数量不超过该枚巡飞弹携带武器的总数。

约束条件3：

式中，sj表示某时刻目标j 受到攻击的最大阈值。该式表明分配给每个目标至少一个武器，且对综合价值较大的目标可分配多个武器同时攻击，但不能超过最大阈值，以免造成弹药浪费，一般取sj=5。

2 DE 算法基本原理

2.1 种群初始化

种群初始化方法，一般如式（10）所示：

2.2 种群变异

父代个体xiG进行变异操作，产生变异体viG；以下的7 种变异策略较为常用：

DE/rand/1：

DE/rand/2：

DE/current to rand/2：

DE/best/1：

DE/best/2：

DE/pbest/1：

DE/current to pbest/2：

2.3 种群交叉

变异体viG与父代个体xiG进行交叉，产生试验体u。试验体由式（18）计算得到：

式中，CR 为交叉率，xiG为第G 代种群的个体（或称为目标体）；uiG+1为第G+1 代的试验个体。条件j=jr是为了保证试验中必有部分基因来源于变异体，jr为［1，D］之间的随机整数。

2.4 种群选择

采用“贪婪策略”，试验体uiG与父代个体xiG执行选择操作，产生下一代个体u。如式（19）所示：

式中，f（·）为适应度函数。

3 DE 算法的改进

3.1 编码

针对复杂的目标分配问题，使用DE 算法求解时，首先需对待解决问题的性质进行全方面的考虑，其次对编码方案进行合适化的选择，其所选方案既要满足所建数学模型的约束条件，还要能对问题的解进行表示［12］。

基于上述考虑，本文选用十进制整数编码方案，每个个体都代表一个可行的解，其具体的编码方式，如图1 所示。

图1 改进的DE 算法求解目标分配问题的编码Fig.1 Encoding of improved DE algorithm for the solution of target allocation problem

编码块由各枚巡飞弹所携带武器预分配的目标编号组成，编码块按各枚巡飞弹顺序排列构成一个种群个体的编码，每种排列代表了一种分配方案。各枚巡飞弹所携带的武器总数决定了个体编码的长度。例如，某次巡飞弹协同攻击作战，第i 枚巡飞弹的所携带武器数为ki，则与该枚巡飞弹对应的编码块长度为ki，编码个体的长度（即编码维度）为D=ki；编码块里的数字代表该编码块所对应巡飞弹的武器预分配的目标编号，且数字须为（1-n）内的整数；如个体的k1段数字为3，4，6，2，表示第1枚巡飞弹有4 个可用武器，第1，2，3，4 个武器分配给3，4，6，2 号目标。

3.2 多种群协作进化

多种群协作进化是指多个种群单独进行交叉变异操作和定期共享信息，从而实现协作进化，提高算法的优化能力［13］。具体步骤如下：1）计算初始种群适应度值；2）排列初始种群的个体（按适应值从大到小顺序）；3）将排名在前Q%的个体存入“特定种群”中（为了方便，这里称“特定种群”为精英种群）；4）将（1-Q）%的种群重新划分为3 个“同等规模的种群”（为了方便，这里将“同等规模的种群”命名为探索种群）；5）每迭代1 次，探索种群和精英种群更新一次；6）当迭代次数超过设定总迭代次数的1/2 时，精英种群的优秀个体参与每个探索种群的变异。

多种群协作进化中，精英种群的任务是保留存在历史进化过程中探索种群的优秀个体，适时引导探索种群向最优搜索方向发展，探索种群的任务是探索更大的解空间，从而使整个种群朝着全局最优的方向发展。在进化的早期阶段，为了保持种群的多样性，探索种群需要不断地进行积极的变异操作，而精英种群仅对其内部的优秀个体进行更新，不干涉探索种群，其目的是避免提前“干预”导致局部优化和收敛。在进化的后期，以精英种群的优秀个体为基本变量，引导种群加速搜索全局最优解，进行种群变异。多次迭代进化之后，精英群体中的优秀个体逐渐逼近全局最优，从而可通过利用精英群体中的优秀个体引导算法向全局最优方向发展。如下页图2 所示。

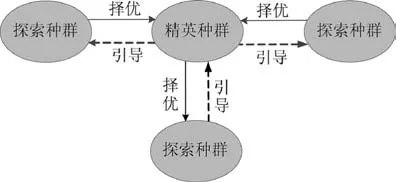
图2 种群协作进化Fig.2 Population collaborative evolution

更新种群的思路为：探索种群每次迭代后，取出前20%的个体组成一个集合（该集合为本次更新产生的精英种群的最佳候选个体）；每次迭代进化后，将集合中个体的适应值与原精英群体中的个体进行比较和替换，如此直至算法迭代完成，最优解即为最后精英种群中适应度值排名第1 的个体。

本文改进的DE 算法中，精英种群规模为10%NP，探索种群自适应选择变异策略、变异率和交叉率。

值得注意的是，精英种群参与进化过程（即引导探索种群的交叉变异），但自身不进化，只更新。

3.3 变异策略的多种选择

在DE 算法中，变异策略不同，起到的效果便会有差异。变异策略的适应性选择是指在种群每次进化中，其内部的个体根据能生成优秀变异体的历史统计信息，对最适用于本代进化的变异策略进行选择［14］。本文改进的DE 算法，探索种群将对DE/rand/1、DE/rand/2、DE/current to rand/2 和DE/current to pbest/2 这4 种变异策略进行适应性选择。变异策略自适应选择和更新步骤，如图3 所示。

图3 变异策略选择与更新Fig.3 Mutation strategy selection and update

其中，步骤1 中选择概率记为P1、P2、P3和P4，步骤4 中选择次数记为num1、num2、num3 和num4，步骤5 中选择次数记为num_best1、num_best2、num_best3和num_best4，其中，步骤1 变异策略的更新方式和步骤6 中选择概率需归一化处理，如式（20）、式（21）所示：

其中，k∈{1，2，3，4}。

在算法中后期阶段（即G＞1/2Gmax时），这一阶段的DE/current to pbest/2 的计算方法需进行变更，计算方法如下：

3.4 自适应变异率F 和交叉率CR

DE 算法进化过程中，变异率F 和交叉率CR 的取值常常很难把握［15］，F 取值偏大或者偏小，都会对算法产生不良影响［16］。为了防止上述情况的出现，本文将变异率F 和交叉率CR 调整为自适应变化。

3.4.1 自适应调整变异率F

设计关于迭代次数的非线性变化函数来调整F，设计公式如下式：

式中，G 为迭代次数；Gmax为最大迭代次数；F0为变异率初值。

3.4.2 自适应调整交叉率CR

设计关于迭代次数的非线性变化函数来调整交叉率CR，设计公式如下式：

式中，CRmin、CRmax分别为最小和最大交叉率。

3.5 算法的流程

1）算法的基本实现流程，如下页图4 所示。

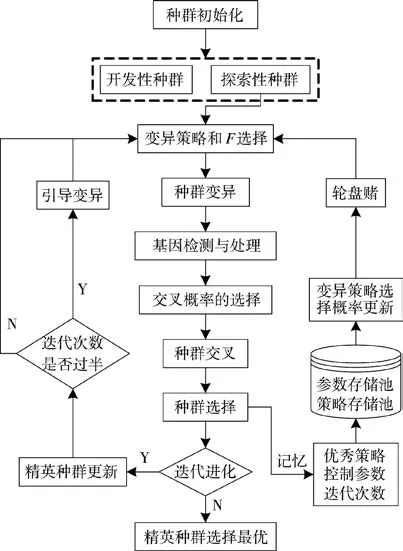
图4 改进DE 算法流程图Fig.4 Flow chart of improved DE algorithm

2）算法步骤。

Step 1 种群初始化，包括种群规模NP、最大迭代次数Gmax，变异率初值F0，最小和最大交叉率CRmax、CRmin等。

Step 2 探索种群独自进行自适应变异率F 如式（23）所示的选择和变异操作，并进行基因检测和处理。

Step 3 探索性种群独自进行自适应交叉率CR的选择如式（24）所示、交叉操作如式（18）所示和选择操作如式（19）所示。

Step 4 更新变异策略的选择概率如式（20）所示。

Step 5 更新精英种群。

Step 6 判断G 是否等于Gmax。若是，则取出精英种群适应度值最大的个体即为最优解；若否，返回Step 2，继续迭代。

4 仿真实验分析

假设我方发射4 枚巡飞弹对敌方阵地的防空导弹车（M1）、坦克（M2）、步兵战车（M3）、指挥车（M4）、雷达车（M5）和装甲运输车（M6）这6 种目标进行协同攻击，4 枚巡飞弹可记为W=（W1，W2，W3，W4），其对携带的武器数量为［4，4，4，3］，目标综合威胁程度为Thi=（0.43，0.25，0.17，0.04，0.05，0.06），权重为0.30，目标造价为Mei=（0.3，0.25，010，0.10，0.15，0.10），权重为0.25；目标任务价值为Ati=（0.25，0.10，0.10，0.30，0.15，0.10），权重为0.45，则目标综合价值Cvi为（0.31，0.18，0.12，0.17，0.12，0.09），目标毁伤概率和目标综合价值如表1 所示（其中目标综合威胁程度、目标造价、目标任务价值及其权重、武器的价值和目标毁伤概率由C3I 专家提供）。

表1 巡飞弹上的武器对目标的毁伤概率Table 1 Probability of damage to targets by weapons on loitering munition

算法仿真实验在Matlab 9.1，AMD R5—4600H CPU 3.0 GHz，16 GB 内存的PC 上运行。设置实验参数：种群规模NP=100，最大迭代次数Gmax=1 000，变异率初值F0=0.65，交叉率：CRmin=0.60，CRmax=0.9。

通过仿真可得到最优个体的编码：［（11 2 2）、（1 1 2 6）、（34 4 4）、（35 5）］，最优适应度值即目标分配最优函数值为f（x）=0.994 0，对应的目标分配决策矩阵为：

适应度值和种群适应度均值变化，如图5 所示。

图5 改进DE 算法的适应度值和适应度均值变化曲线Fig.5 The fitness value and fitness mean change curve of the improved DE algorithm

4.1 改进DE 算法与标准DE 算法的比较

标准DE 算法与本文改进的算法都采用同样的变异、交叉和选择机制，不同的是标准DE 算法中的交叉、变异率是不变值，且其采用单一的变异策略，而改进的DE 算法采用变异策略、变异率和交叉率是自适应的。经过仿真得到改进的DE 算法与标准的DE 算法采用DE/rand/1、DE/rand/2、DE/current to rand/2 和DE/current to pbest/2 模式对比的适应度值变化曲线，如下页图6 所示。

图6 改进DE 算法与各模式的适应度值曲线Fig.6 Improved DE algorithm and fitness value curves for each mode

从图5 和图6 可以看出，本文改进的DE 算法与分别采用4 种变异策略的标准DE 算法相比，具有更好的适应度值（即最优解）和收敛性，即该算法在迭代278 次时，就求解出了最优解且高达0.994 0。

4.2 改进DE 算法与不同算法的比较

分别采用SA-PSO 算法［5］、AI 算法［17］和改进的DE 算法进行求解，进行600 次迭代进化后，得到了3 种算法的适应度变化对比曲线及算法对比，如图7 所示和表2 所示。

表2 3 种算法最优解和迭代次数对比Table 2 Comparison of optimal solutions and iteration times of three kinds of algorithms

图7 3 种算法的对比曲线Fig.7 Comparison curves of three kinds of algorithms

由图7 和表2 可知，随着不断的迭代进化，这3种算法的适应度值不断增加，且最后趋于稳定；AI算法能够在较短时间内找到最优解，但找到的最优解较差；与AI 算法相比，改进的PSO 算法找到的最优解较好，但需要多次迭代进化，其收敛性能较差；本文改进的DE 算法相比改进的PSO 算法和AI 算法而言，能在较少的迭代次数下找到更好的最优解，说明本文改进的DE 算法具有很好的收敛性和全局寻优性。

5 结论

为了使协同作战指挥决策系统能更快、更合理进行目标分配，提出一种改进的DE 算法，采用精英种群引导“探索性”种群协作进化，以提高算法全局搜索和开发性能；采用变异策略自适应选择，以提高算法收敛性和全局寻优能力；采用自适应调整变异率F 和交叉率CR，以满足进化过程中种群对控制参数的要求。本文改进的DE 算法，提高了局部寻优精度、收敛性以及全局寻优性，该算法可用于解决大规模的目标分配问题，并且能快速、有效地求解出符合多巡飞弹-多目标分配模型要求的最优解。