基于BES-ELM的风电机组故障诊断

王俊,席芳,周川,蔡彦枫,王洁,王金城,许昌

(1. 广东科诺勘测工程有限公司,广东 广州 510663; 2. 中国能源建设集团广东省电力设计研究院有限公司,广东 广州 510663; 3. 中交智慧城市生态发展(广州)有限公司,广东 广州 510290; 4. 河海大学能源与电气学院,江苏 南京 211100)

风能作为一种清洁且与环境友好的可再生能源,具有低碳耗、低污染、低排放的特点[1].为了应对环境污染破坏所导致的全球变暖和能源危机等一系列问题,诸多国家积极发展风电产业寻求能源替代品,使得风电机组累计装机容量快速平稳增长.世界风能协会在2021年3月24日公布的风力发电统计相关数据显示,2020年全球风力发电总装机容量已达744 GW[2].

风电场通常坐落于偏远山区、草原、戈壁滩、沿海滩涂或近海等风能资源较丰富但环境相对较恶劣的区域,工作环境复杂多变,易受不稳定载荷与不可控因素影响,这些工况条件增加了风电机组故障的发生率[3].随着机组装机总量的提升,发生故障的机组比例也逐步提高,有效的故障诊断技术显得颇为重要.它能帮助运行维护人员及时发现机组的异常运行状态,快速分辨故障类型并采取相应的措施,在很大程度上减少故障对机组及电网的影响,确保整个风电场能够安全平稳、经济高效地运作[4].目前,SCADA系统多被应用于采集风电机组运行的关键参数,并搭建相应的数据库存储数据,可用于大数据分析机组运行状态,搭建数据驱动的故障诊断模型[5].

在风电机组故障诊断检测技术中,人工神经网 络(ANN)[6]、支持向量机(SVM)[7]和极限学习机 (ELM)[8]是应用较为广泛的分类算法.ELM具有学习速度快、泛化能力强、诊断精确度高等优点.但采用ELM网络模型时,需要人工设置输入层权重w和隐藏层偏置b等相关参数,若设置不当可能会导致故障诊断精度的降低.针对ELM模型对相关参数值要求较高的问题,文中提出一种基于秃鹰搜索(bald eagle search,BES)算法优化的ELM模型,并采用这个模型对风电机组故障进行分类.文中主要进行以下工作:① 构建BES-ELM故障诊断模型.通过BES算法优化ELM的输入层权重w和隐藏层偏置b,使用优化后的参数搭建诊断模型.② 对原始SCADA数据预处理,得到故障数据集,并把这些故障数据作为训练数据,分别采用ELM, GA-ELM, POS-ELM和BES-ELM模型进行故障分类,比较其分类效果.

1 研究方法

1.1 秃鹰搜索算法

秃鹰搜索算法是ALSATTAR等[9]、贾鹤鸣等[10]受秃鹰狩猎行为的启发而提出的一种新型群智能优化算法.它不受目标函数可微、可导、连续性等特性的限制,具有较强的全局搜索能力、较好的稳定性、收敛速度快等特点.

BES搜索算法模拟捕食猎物的行为,将其分为选择搜索空间、搜索猎物和俯冲捕获猎物等3个阶段.

1) 选择搜索空间阶段:在此阶段,秃鹰随机选择搜索区域,寻找猎物数量最多的区域.该阶段的位置更新描述为

(1)

2) 搜索猎物阶段:秃鹰在搜索猎物阶段,在选定的空间内以螺旋形状飞行搜索猎物,并在螺旋形空间内以不同的方向移动,锁定猎物位置之后加快搜索速度,寻找最佳俯冲捕获位置.螺旋飞行位置更新描述为

θ(i)=β·π·rand(0,1),

(2)

r(i)=θ(i)+γ·rand(0,1),

(3)

x·r(i)=r(i)·sin(θ(i)),

(4)

y·r(i)=r(i)·cos(θ(i)),

(5)

(6)

(7)

式中:θ(i)为螺旋方程的极角;r(i)为螺旋方程的极径;β,γ为控制螺旋轨迹的参数,β∈(0,5),γ∈(0.5,2.0);x(i)与y(i)为极坐标中位置,取值均为 (-1,1).位置更新为

(8)

式中:Li+1为第i只秃鹰下一次更新位置.

3) 俯冲捕获猎物阶段:秃鹰从搜索空间的最佳位置快速俯冲飞向目标猎物,种群其他个体也同时向最佳位置移动并攻击猎物,该阶段的运动状态仍用极坐标方程描述,即

(9)

δx=x1(i)·(Li-c1·Lmean),

(10)

δy=y1(i)·(Li-c2·Lbest),

(11)

式中:c1,c2为秃鹰向最佳与中心位置的运动强度,c1,c2∈[1,2].

为了验证BES的优越性,分别采用粒子群优化(particle swarm optimization, PSO)[11]、灰狼搜索(grey wolf optimization, GWO)[12]与鲸鱼搜索(whale optimization algorithm, WOA)[13]等算法进行几个基准测试函数的对比试验,试验中被采用的基准测试函数如表1所示,其中F1,F2为单峰测试函数,F3,F4为多峰测试函数,为复合函数,D为维度.

表1 基准测试函数

4种算法的种群规模统一设为20,最大迭代次数设为1 000,每种算法分别对各个测试函数进行20次独立试验,统计20次独立试验得到的每种算法对各测试函数求解的最优解、平均值、标准差作为评价指标,试验结果如表2所示.

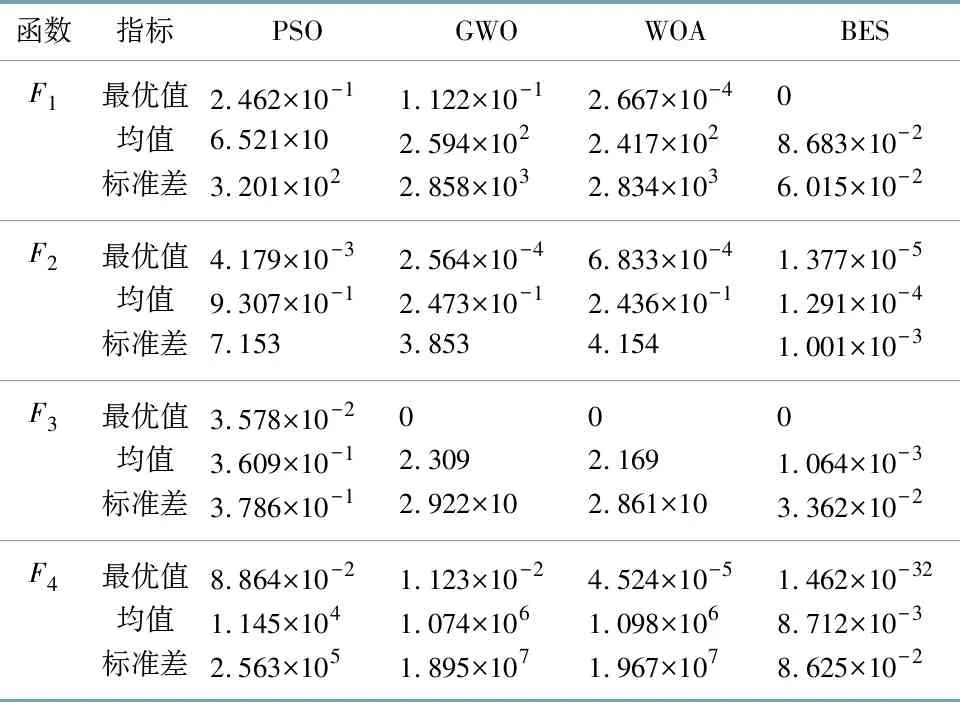
表2 测试结果

其中BES在基准测试函数F1和F3中的收敛最优值与理论最优值一致,在基准测试函数F2和F4中的收敛最优值分别为1.377×10-5和1.462×10-32.BES在4种基准测试函数中收敛的最优值均低于PSO,GWO和WOA对应的最优值.

由表2可知,与PSO,GWO,WOA相比,BES的收敛精度最好.

1.2 极限学习机

极限学习机ELM是在传统前馈神经网络的基础上提出的一种神经网络模型[14-15].在运算过程中,ELM网络的输入权值和偏置是随机给定的,然后在保持神经网络特性的前提下,使用正则化原则计算并获得输出权值.

ELM网络中的输入层和输出层均为1层,而隐含层可以是1层或者多层.在此算法中,输入层和隐含层是由输入权值连接,隐含层和输出层之间由输出权值连接,权值和偏置是随机生成的.通过在训练过程中设置隐藏层的数量,容易得到唯一的最佳解决方案.设n,l,m分别为输入层、隐含层、输出层的节点数,g(x)为隐藏的激励函数,则对应的ELM网络结构如图1所示.

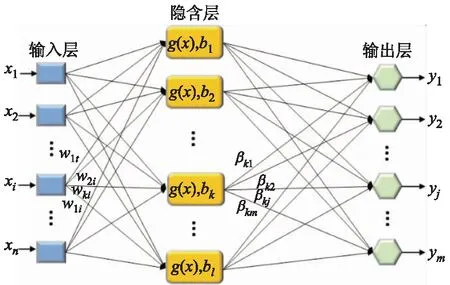
图1 ELM网络结构

如图1所示,输入层的神经元数量与输入变量、输出层的神经元数量与输出变量均是一一对应的,其中输入层对应n个相关变量,输出层对应m个相关变量;含有l个神经元的隐含层为中间连接层,通过输入权值w与输入层连接,通过输出权值β与输出层连接,2个权值的表达式为

(12)

(13)

式中:wki,βkj分别为单一神经元之间的连接权值和偏置;k记为连接隐含层第k个的神经元编号;i,j分别代表输入层第i个神经元与输出层第j个神经元的编号.设有Z个样本的训练集输入矩阵X和输出矩阵Y分别为

(14)

(15)

隐含层神经元的激活函数为g(x),偏置b=[b1b2…bk…bl]T,则这ELM网络的输出T为

T=[t1,t2,…,tZ]m×Z,

(16)

(17)

式中:wi=[wi1,wi2,… ,win];xj=[w1j,w2j,… ,wnj]T.

则式(17)可表示为

Hb=T′,

(18)

H=[w1,w2,...,wl,b1,b2,...,bl,x1,x2,...,xZ],

(19)

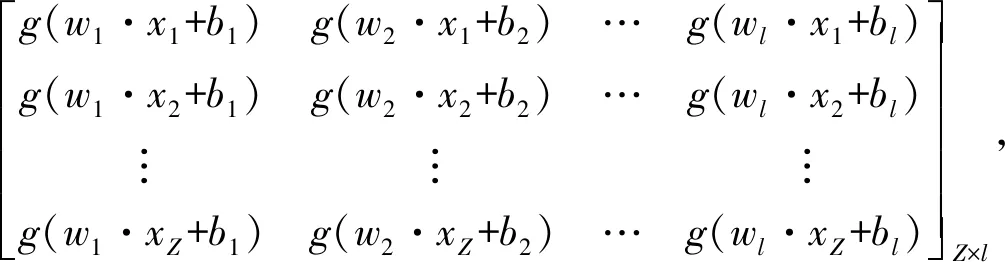
(20)

式中:Τ′为矩阵T的转置;H为ELM网络隐藏层的输出矩阵.

在训练过程中,输出层权重β是通过最小化损失函数来计算的.损失函数由训练误差项和输出层权重范数的正则项组成.而该式可使用Moore-Penrose广义逆矩阵理论计算求得最优权重,即

(21)

(22)

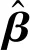
2 BES-ELM模型

在ELM计算过程中,相关参数的选择对分类结果有很大影响.通过BES算法对ELM的输入层权值w和隐藏层偏置b进行优化,能够获得较优的参数组合{w,b}.BES算法优化ELM相关参数的流程如图2所示,具体计算步骤为

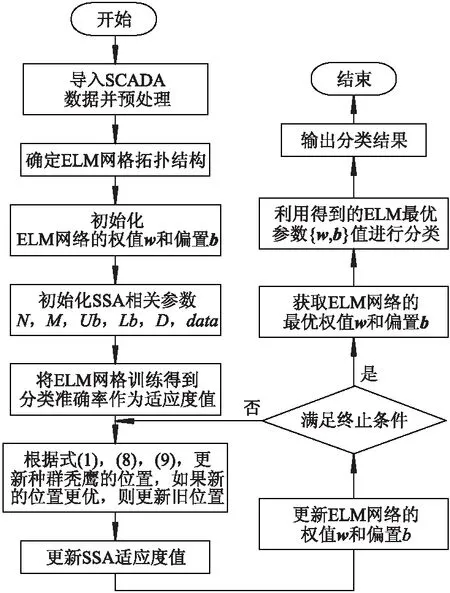
图2 BES-ELM模型流程图

步骤1:对原有SCADA数据进行预处理,将其分成训练集和测试集后导入算法中.

步骤2:根据训练集数据,确定ELM网络的输入层、隐含层、输出层节点数量,确定ELM网络拓扑结构.

步骤3:初始化ELM网络,随机取值并赋值给ELM网络的权值w和偏置b.

步骤4:根据样本数据特征,设置BES算法的种群数量N、最大迭代次数M、自变量上限Ub、自变量下限Lb、维度D等相关参数.

步骤5:根据权值w和偏置b的初始值训练ELM网络,将训练得到的分类准确率作为适应度值.

步骤6:利用文中公式(1),(8),(9)计算获取秃鹰新位置对应的适应度值,并将该值与原值进行对比,如果新的适应度值更优,则更新取值.

步骤7:在ELM网络训练过程中当前的适应度值随秃鹰位置变动而实时更新,不断保存最优的适应度值,及其对应的ELM的权值w和偏置b.

步骤8:如果满足算法中设置的终止条件,则直接跳出该循环,同时输出ELM最优的参数组合{w,b}及其对应的最优适应度值;如果不满足,则迭代次数加1,跳转执行步骤6.

步骤9:获取ELM网络的最优权值w和偏置b,并根据最优参数组合{w,b}搭建ELM网络.

步骤10:使用已选取的样本对ELM网络进行训练,并输出分类结果.

3 实例分析

3.1 SCADA数据预处理

为验证BES-ELM诊断模型的性能,文中采用风电机组在4种状态下的相关数据作为故障分析数据,它们分别为发电机过热状态(S1)、馈电故障状态(S2)、变流器冷却系统故障状态(S3)和正常状态(S4).相关的特征参数如表3所示.

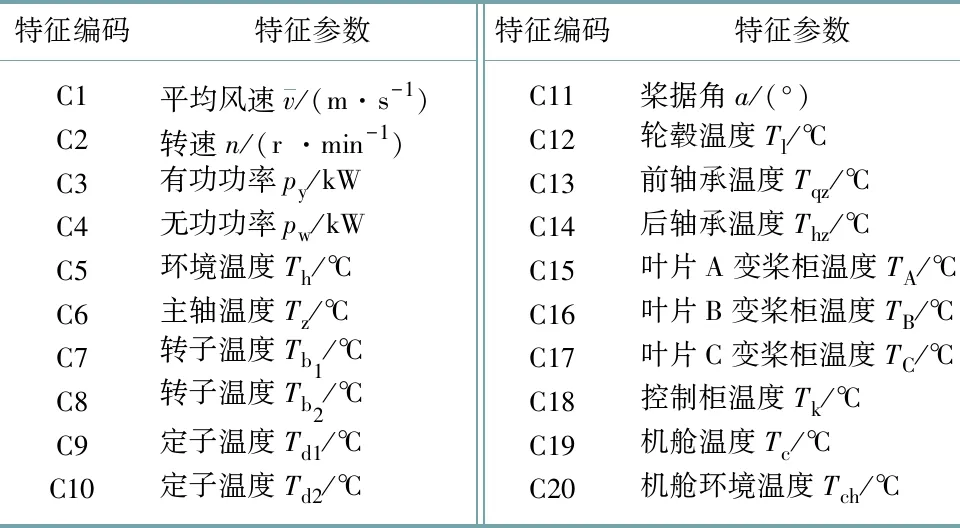
表3 特征编号及描述

试验总共选取了800个样本,其中560个为训练样本,240个为测试样本.在4种状态中,每个状态选取了200个样本,其中140个为训练样本,60个为测试样本.部分样本归一化后的特征值如表4所示.

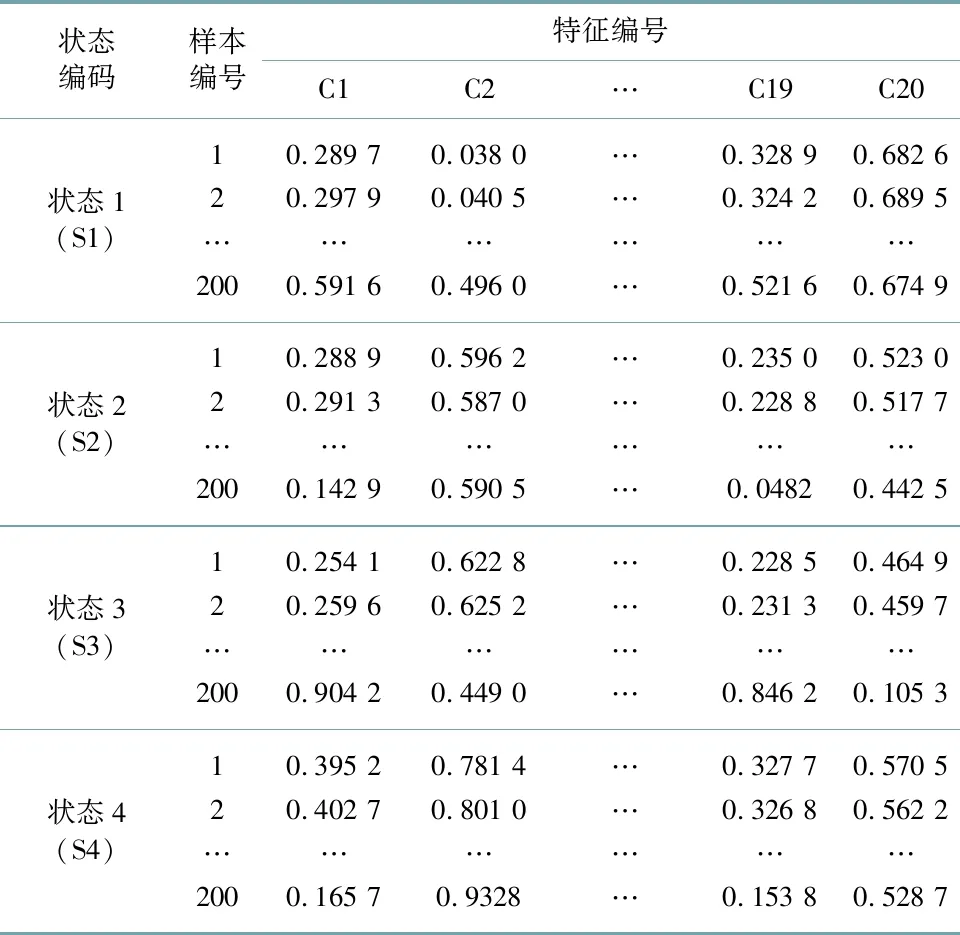
表4 风电机组的4个状态特征样本

3.2 模型的参数设置

为体现模型的故障识别与分类能力,文中分别使用遗传算法、粒子群算法和秃鹰搜索算法来优化ELM的参数,相关参数设置值如表5所示.

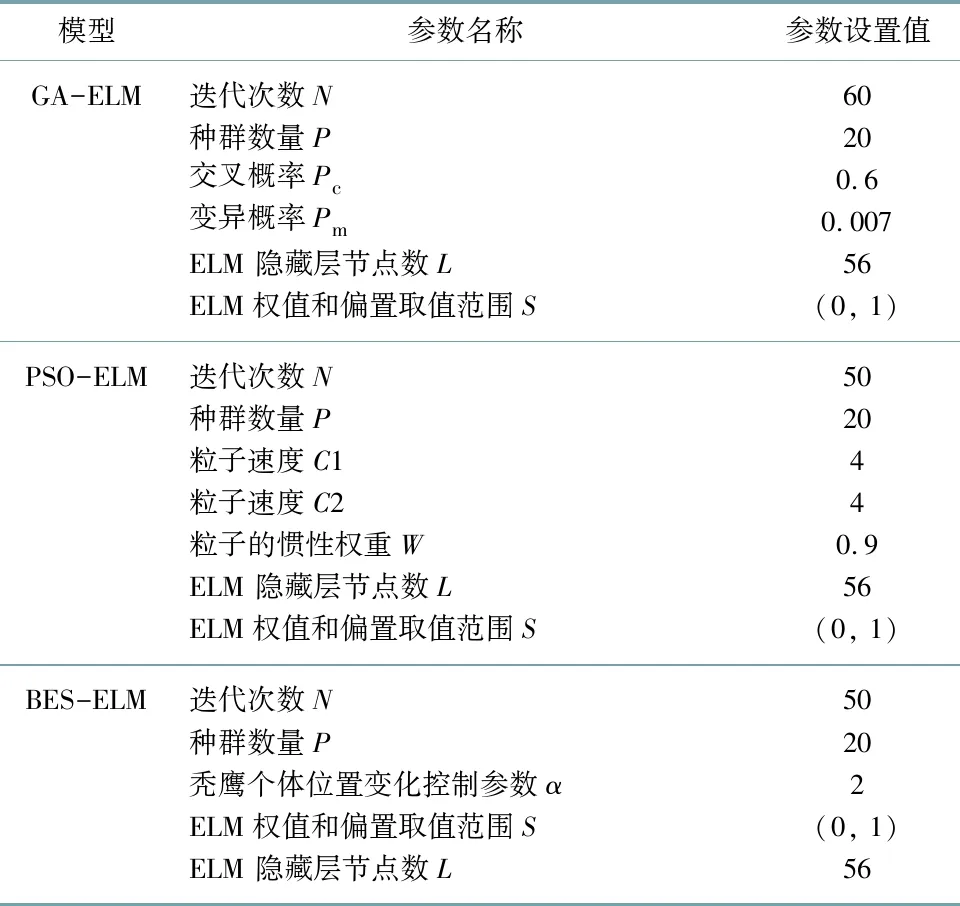
表5 GA-ELM, PSO-ELM, BES-ELM模型的参数设置表

3.3 模型性能比较

文中BES-ELM 与GA-ELM,PSO- ELM模型进行寻优适应度值比较,其结果如图3所示,图中I为模型的运行次数,A为准确率.BES-ELM模型第6次运行时搜索到最优值(98.75%);PSO-ELM模型第14次运行时基本达到最优值(96.25%),而GA-ELM模型到达最优值(92.08%)需要运行到第26次.采用BES算法对ELM参数优化后寻优速度最快且诊断准确率最高,PSO-ELM算法次之,而GA-ELM算法最低.

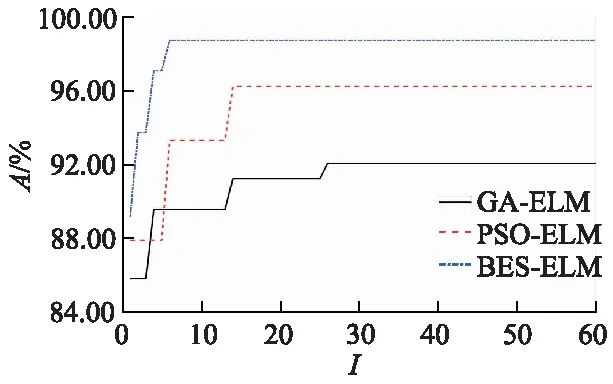
图3 3种模型迭代次数与适应度关系

为了进一步直观地体现BES-ELM模型在风电机组故障诊断的优势,用标准ELM,GA-ELM,PSO- ELM等模型分别计算并绘制了混淆矩阵,即如图4所示.

图4 4种模型的混淆矩阵

标准ELM模型能准确分类状态S2和S4,原属于状态S1的17个样本错判为状态S3.在240个测试样本中,标准ELM模型能准确分类213个.BES-ELM模型能准确分类状态S1,S2和S4,只有原属于状态S3的3个样本误判为状态S4.BES-ELM模型能准确分类237个,在所用的分类模型中它准确分类的样本数量最多.表6为故障诊断模型的性能指标.

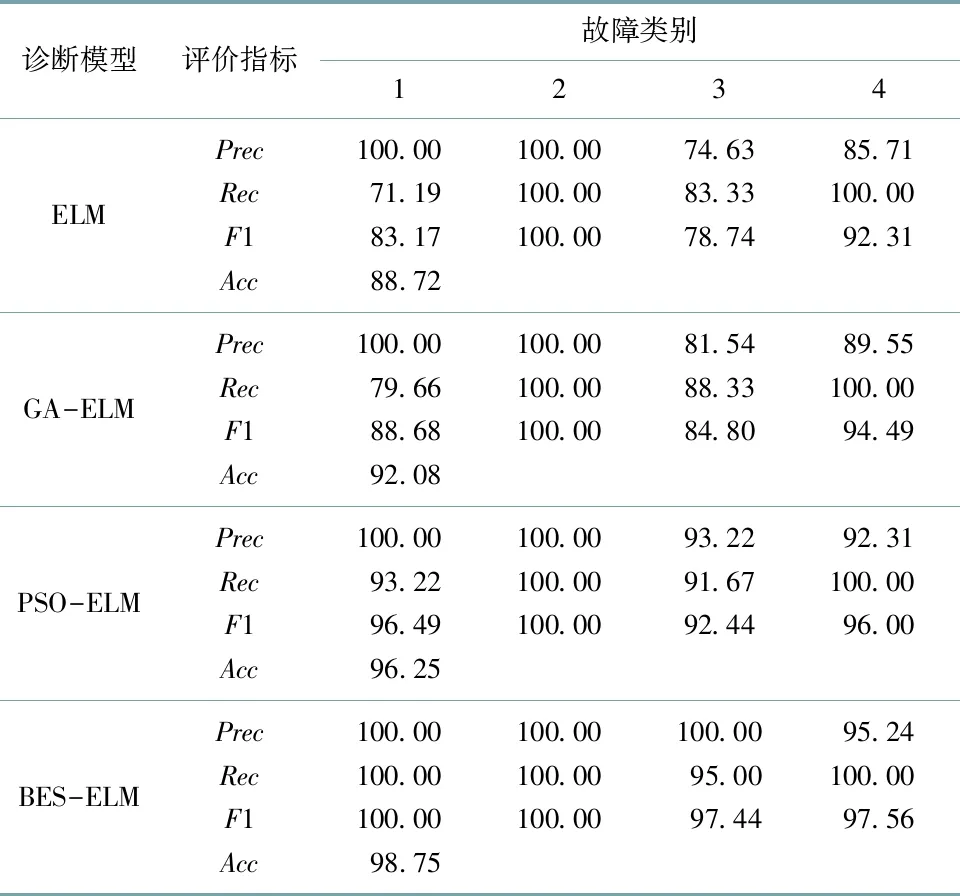
表6 故障诊断模型的性能指标

为进一步显示这些模型的诊断性能,分别计算精度(Prec)、召回率(Rec)、F1值和准确率Acc等分类性能指标,其计算结果如表6所示.当使用BES-ELM模型进行故障诊断时,诊断准确率达到98.75%,优于其他3种诊断模型,能够较好地完成对风电机组故障诊断的任务.

4 结 论

作为一种前馈神经网络,ELM具有学习速度快、泛化能力强等优点.但是相关参数设置不当易导致ELM分类准确率较低.针对该问题,文中采用秃鹰搜索算法对ELM相关参数的选取进行优化,提出了BES-ELM模型,可较大程度上弥补ELM模型的不足.

1) 采用BES算法优化ELM的权值w和偏置b的参数,有效提高了ELM模型分类的准确率.用秃鹰搜索算法优化后的极限学习机在风电机组故障诊断试验中表现较好,它的分类性能指标均优于标准ELM,GA-ELM和PSO-ELM,在测试集上的分类准确率也达到了98.75%.

2) 在风电机组的典型故障诊断中,虽然BES-ELM的分类准确率已经很高,但仍有一些困难问题需要解决,比如难以区分一些复杂的故障情况,分类的准确率仍需要进一步提高等.探索其他更适合的故障特征提取和特征选择方法有助于提高该模型的分类精度,提高故障数据集的质量将有助于模型的强化训练,这些都是下一步的研究方向.