时序效应对多级侧流道泵压力脉动的影响

宋梦斌,刘润石,陈轲,王业芳,张帆*

(1. 利欧集团湖南泵业有限公司,湖南 湘潭 411201;2. 江苏大学国家水泵及系统工程技术研究中心,江苏 镇江 212013)

侧流道泵是一种特殊的旋涡泵,其拥有流量小、扬程高、可自吸、气液混输能力强等优点,一般运用于化工、汽车、医药工业和油气开采等场所.与传统旋涡泵相比,侧流道泵结构特殊,其只在叶轮一侧具有空间流道.根据叶轮数量,侧流道泵可分为单级侧流道泵和多级侧流道泵.为了提升空化性能,通常会在多级侧流道泵首级处设置离心叶轮以提高径向叶轮的进口压力.

20世纪初期,SIEMEN等[1]首次提出侧流道泵的结构.RITTER等[2]于1930年提出侧流道泵内部流体的流动规律.SCHMIEDCHEN等[3]于1932年进一步分析了几何参数对于侧流道泵性能的影响,定义了工作系数.PFLEIDERER等[4]于1949年对前两者的研究做了系统性的总结,并利用动量交换理论对侧流道泵的水力性能进行分析计算.2005年,MEAKHAIL等[5]对于侧流道泵的内部流动提出了新的见解,认为流体不仅仅从叶尖区域进入侧流道,也从叶片中上部离开叶轮区域进入侧流道.由此,修正了侧流道泵的扬程和效率的计算公式,并发现叶片侧出口角对于侧流道泵的性能有较大影响.

近年来,张帆[6]发现叶片吸力角的增加对侧流道泵内部的流动交换有利,提升了侧流道泵的性能.魏雪园[7]设计了小凸形叶片,这对于拓宽侧流道泵高效区有所帮助.WANG等[8]研究CFD中不同湍流模型对于模拟结果的影响,指出SAS模型和FBM模型的模拟结果与试验结果更加接近.张帆等[6,9]指出侧流道泵与常规叶片泵不同,其压力脉动的主要影响因素是叶轮与侧流道间的流体交换次数.同时,随着叶片吸力角的增大,压力脉动在频率不变的情况下幅度增大.陈轲等[10]基于MUSIG模型对气液混输下侧流道泵内压力脉动进行了研究,发现在低进口含气率下压力脉动主频与含气率无关,但在少量通气下会导致轴向间隙部分出现高强度压力脉动.

另一方面,WALKER等[11]在对某1.5级轴流压气机的研究中发现,静止部件的相对周向位置能够对其机械性能和整体噪声产生显著影响.对于旋转部件间的时序效应研究则始于1998年,CIZMAS等[12]对某型涡轮机研究中发现,旋转部件之间也存在明显的时序效应,且其影响是静止部件之间时序效应影响的2倍,由此提出全时序效应理论(Fully Clocking Effect理论).2015年,谈明高等[13]以一台多级离心泵作为研究对象,发现合适的交错角能够有效利用相反的压力脉动减小振动幅度.

从国内外研究现状可知,目前侧流道泵的运行原理、压力脉动特性、非定常流动特性、性能优化研究已经比较完善,然而,对于多级侧流道泵各级叶轮和侧流道之间互相干涉的研究仍然处于初级阶段,尤其是叶轮和流道之间的时序效应对侧流道泵的性能影响目前还鲜有涉及.文中针对多级侧流道泵,深入分析时序位置对多级侧流道泵的压力脉动影响规律.

1 压力脉动分析方法

文中首先采用傅里叶变换分析压力脉动频域特性,再利用小波分解分析其时域信息.

1.1 傅里叶变换

傅里叶变换是一种常用于频谱分析的研究方法,通过式(1)将任意周期函数分解为若干不同正弦波的和.

(1)

虽然傅里叶变换可进行频谱分析,但它不能表征出信号的局部特性,对于突变和非平稳信号分析不准确,显示不出时域信息.

1.2 小波变换

小波分析是一个时间和频率的局域变换,它能有效地从信号中提取信息,通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析.小波分析解决了短时傅里叶变换的缺点,其窗口是可变的,从而使其能够兼顾时域和频域的精度[15].小波变换的基础公式如式(2),(3)所示.

(2)

(3)

式中:a为尺度变量,控制小波的伸缩,对应频率变化;τ为平移变量,控制小波的平移,对应时间变化.

选取Matlab作为小波分解软件,选取Daubechies小波(DB小波簇)作为分解的小波簇.因本研究中主要目的是分析其在不同时序位置下稳定运行时的非定常压力脉动规律,故经过分析采用DB4小波进行分解,分解层数为4.

2 模型建立与边界层设置

选取带有前置离心叶轮的三级侧流道泵作为研究对象,该泵进口直径为40 mm,出口直径为32 mm.其离心叶轮有6枚叶片,进出口外径分别为40 mm和120 mm.径向叶轮有24枚叶片,叶片宽度为10 mm,叶片厚度为5.4 mm,叶片外径为130 mm.原型泵中两级侧流道相关部件周向相差180°.该泵内水体极为复杂,难以进行结构化网格划分,因而只对旋转部件进行结构化网格划分,其他部位采用非结构化网格划分.

为确定最佳的网格数,对所绘制的网格进行网格独立性验证.当网格数量为3 000万左右时,扬程曲线趋于平缓,而效率曲线始终平缓,故后续模拟用模型的网格数量为3 000万.另一方面,网格的模拟效果不仅仅与网格数量有关,还需要通过参量Y+值验证网格合理性及计算结果的准确性[7],其定义式为

(4)

式中:τw为壁面切应力,Pa;ρ为流体密度,kg/m3;Δn为离壁面最近2个网格点间距离,m;ν则是运动黏度,m2/s.由式(4)所定义的Y+是一个纲量为一的量,在拟采用的网格模型中,所得到的旋转部件表面Y+云图如图1所示.由图可知,静止区域壁面平均Y+值为73.20,旋转区域壁面平均Y+值为32.43.根据文献[6]可知,文中网格能够满足模拟要求.

图1 旋转部件表面Y+云图

选取设计工况点作为模拟工况点,其转速为2 900 r/min,流量为4.00 m3/h.采用DES-CC模型作为非定常模拟的湍流模型.在进出口方面,采用质量流量出口和静压进口的设置;选择Upwind作为网格空间离散设置以获得更好的鲁棒性.考虑到泵的运行环境,采用25 ℃的水作为流体,并将传热模型设置为等温模型.壁面无滑移,同时由于原型泵内部流道大多数壁面比较粗糙,因此,对于表面进行过精加工的径向叶轮,将粗糙度设为0.05 mm;对于内部流道存在明显铸造痕迹且没有精加工痕迹的其他部件,将粗糙度设为0.25 mm.在非定常模拟中,选取瞬态转子-定子作为动静交界面设置.文中以叶轮旋转1°角所需要的时间作为瞬态时间步长,计算稳定后叶轮旋转1周所需时间内的流动情况.监测点的选取对于计算多级侧流道泵的压力脉动十分重要.选取两级径向叶轮每错3°角为一个时序位置,共选取5组作为时序效应的原始组和时序对照组,简称位置1,2,3,4,5.以旋转轴为z轴,流向为正向,选取叶轮几何中心为原点建立柱坐标系,如图2所示.在两级径向叶轮的叶根、叶中、叶尖各取9个监测点,如图3所示.监测点1—9的坐标(z,r)依次为(-5,35),(-5,50),(-5,65),(0,35),(0,50),(0,65),(5,35),(5,50),(5,65).同时,取进口段延长中心和出口段延长中心2个监测点,共20个监测点监测静压和总压,用于分析在不同工况、不同时间节点和不同时序位置上两级径向叶轮和多级侧流道泵整体上的压力脉动分布规律.

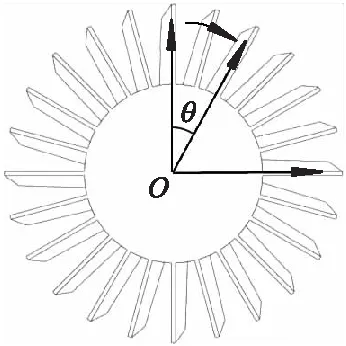
图2 多级侧流道泵时序位置变化角

图3 多级侧流道泵内部压力脉动监测点位置

3 结果与讨论

3.1 出口处压力脉动对比

由于在模拟设置时采用静压进口,因而进口处的压力脉动几乎不存在,故只对出口处进行压力脉动对比分析.

3.1.1 时域特性分析

图4为出口压力监测点的时域分布图,图中p为压力,T为时间步.图中以ca表示分解出的主波,cd表示分解出的杂波,以数字代表分解层数.由图4可知,小波分解能够有效地区分压力脉动中的不规则杂波,并将由前置离心叶轮引起的干扰分离出来,进行有效过滤.在1个脉动周期里,压力出现2次上升和2次下降,因而出现了一高一低的2个波峰和波谷.同时还发现,在不同的时序位置下,压力脉动的幅度存在差异.具体而言,当时序位置为θ=6°和θ=9°时,压力脉动的幅度相对较小和相近,其高波峰下降,低波峰上升.这说明动态时序效应对于提高多级侧流道泵的出口压力脉动具有积极作用.

图4 出口压力监测点的时域分布图

3.1.2 频域特性分析

图5为出口压力监测点的频域分布图.图中FFT为频域幅值,f为频率.由图可以发现,改变时序位置并不能对多级侧流道泵的整体频域产生足够的影响.此外,频域上出现明显的波峰,且这些波峰符合叶轮机械压力脉动的普遍理论.

图5 出口压力监测点的频域分布图

选取频域峰值点进行分析,发现其峰值位置都处于1 160 Hz的倍频位置,具体幅值如表1所示.

表1 出口的压力脉动频域特征

通过表1可知,不同时序位置出口脉动主频基本一致,平均幅值则存在差异,位置1幅值最大,位置3和位置4次之,位置2和位置5最小,位置1平均幅值较位置5大15.7%,位置3和位置4的平均幅值较位置5分别大8.3%和8.8%.综合考虑时域的情况,发现动态时序效应对于多级侧流道泵的压力脉动具有明显的影响.通过选择合适的动态时序位置,可以有效抑制多级侧流道泵出口的压力脉动幅度.

3.2 径向叶轮内压力脉动对比

研究发现,未改变时序位置的第一级径向叶轮内部压力脉动并未发生明显变化.因此,文中只对第二级径向叶轮内部压力脉动进行详细分析.

3.2.1 时域特性分析

第二级径向叶轮监测点1的压力脉动时域分布如图6所示.由图可知,不同的时序位置下,压力脉动的幅度会有所变化.试验结果表明,在时序位置3和位置4时,压力脉动幅度最小.为更好地观察压力脉动的情况,采用了小波分解的方法,将高频杂波从信号中分离出来.利用第二级分解方法,有效排除了前置离心叶轮的影响,成功从分离出的杂波中发现了前置六叶离心叶轮对压力脉动的影响,其脉动幅值呈现出在1个周期内先升后降的趋势,但由于其最大幅值也不能够达到主脉动的5%,因而在主脉动中不显著.在此后只对小波分解后的主波进行分析.

图6 压力监测点1的时域分布图

图7为监测点2—9在不同时序位置的压力脉动时域分布图(ca2).由图7a可以发现,时序位置1和位置2的压力脉动趋势与其他时序位置有所不同,这值得进一步研究其原因.此外,还发现压力脉动的幅度会随时序位置的变化而变化,这进一步证明了动态时序效应对侧流道泵压力脉动的影响.由图7b可知,监测点3脉动波峰值较监测点1和监测点2更高,这是由于监测点3位于叶尖,此处压力相对更高.由图7c可以发现,随着叶片的转动,监测点4叶根区域的压力逐渐提升.同时还观察到,监测点1的数据与监测点4的数据非常相似,压力脉动的幅值和整体变化趋势基本一致,在相同的时刻压力按相同的规律上升,并在相同的时刻压力陡降.这表明,叶根区域的不同位置可能不存在较大的压力脉动差异.将图7d监测点5的结果与其他同叶高区域的监测点进行比较,发现监测点5的压力脉动变化更大,并且相对较高,与叶根区域比较同样体现了这一情况.这表明,当流体从叶根区域流向叶中时,其动能得到增加,从而使其压力升高.由图7e可以发现,监测点6的情况相对平缓,与监测点5有所不同.试验结果显示,时序位置3和位置4的压力脉动幅度最小.图7f中监测点7的结果进一步证实了在叶根区域压力脉动情况差距不大的事实.在这一轴向位置的3个监测点中,只有监测点7的压力水平随着叶轮的转动而逐渐上升.监测点8和监测点9的压力脉动大致相似,与监测点7不同的是,它们呈现出较为平缓的压力脉动,没有出现压力大幅上升而后陡降的现象.

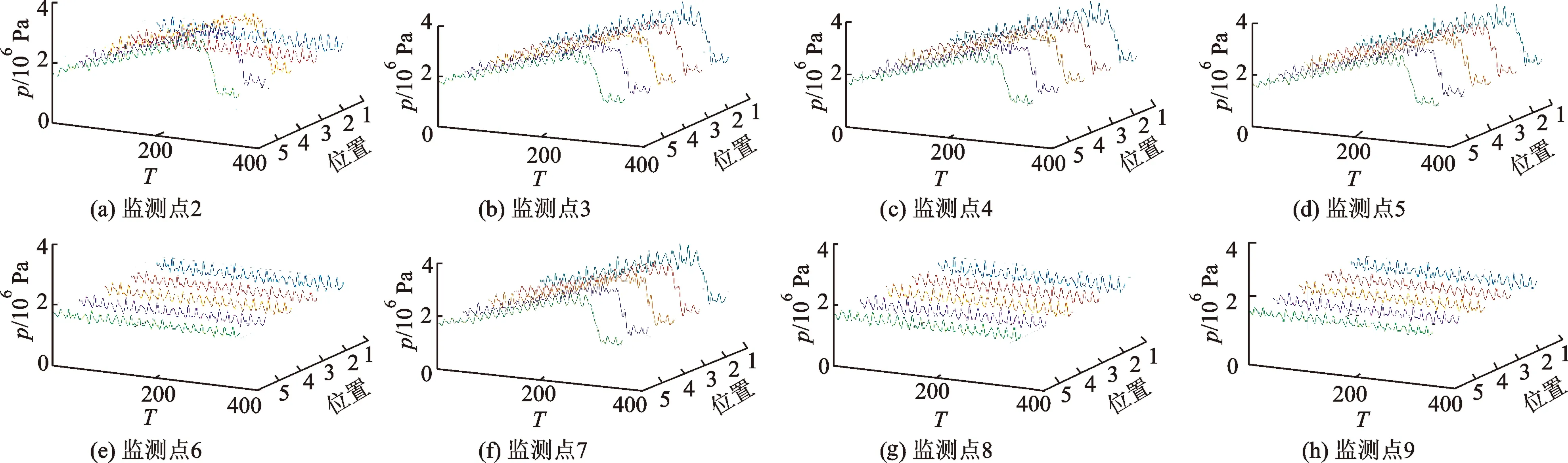
图7 压力监测点2—9的时域分布

由上述压力分布曲线可知,所有监测点验证了适当的时序位置(位置3和位置4)可以有效降低压力脉动幅度,且下降幅度约为7%.多级侧流道泵的最佳时序位置可能与级数成反比,而与夹角成正比.虽然不同监测点的波动有各自的特点,但选择合适的时序位置仍然是降低多级侧流道泵压力脉动的有效方法,最大可降低7%以上的压力脉动幅度.如果此优化对频域影响不大,那么选择合适的时序位置就是有效的.

3.2.2 频域特性分析

为了研究某一特征点的频域特征,选取监测点1进行观测.图8为压力监测点1的频域分布图,图中监测点1的频域分布显示其固有频率仍为倍轴频,并且时序位置的调整对其没有影响;选取频域峰值点进行分析,发现其峰值位置都处于1 160 Hz的倍频位置,具体幅值如表2所示.

表2 监测点1的压力脉动频域特征

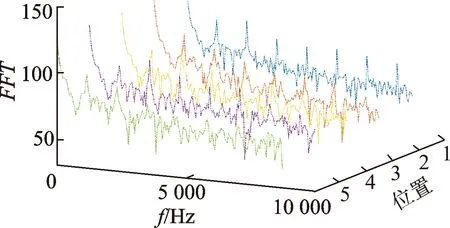
图8 压力监测点1的频域分布图

由表2可知,不同时序位置监测点1脉动主频基本一致,平均幅值则存在差异,位置1幅值最大,位置3和位置4次之,位置2和位置5最小,这与出口压力脉动的现象一致.其他监测点的频域曲线与该点基本一致,说明动态时序效应对压力脉动的频率影响不足.因此,合适的时序位置调整不会对多级侧流道泵的整体共振频率造成较大的改变.同时,这也意味着在设计多级侧流道泵时,不需要针对其共振条件进行特殊的修改,只需要关注适当的时序位置调整即可有效地减少压力脉动对泵的影响.

4 结 论

1) 通过合适的时序调整,可有效降低压力脉动幅度.此外,叶轮的周向排布对压力脉动的影响也很重要,其中错位角与叶轮级数和叶片数成反比例关系.因此,在设计多级侧流道泵时,需要考虑时序调整和叶轮的周向排布等因素,以最大程度地减小压力脉动.

2) 合适的时序位置调整可以减轻压力脉动的共振现象,但不会显著改变泵的整体共振频率.因此,在设计多级侧流道泵时,不需要针对其共振条件进行修改,而可以通过适当的时序位置调整来减小压力脉动对泵的影响.

3) 通过合适的时序位置调整,可以控制侧流道泵整体的振动和出口压力的稳定性,从而提高侧流道泵的性能.因此,在设计和运行侧流道泵时,需要注意时序位置的优化调整,以获得最佳的性能.