一类非线性系统的有限时间有界跟踪控制
2023-10-26孙怀辉姚玉武产黄峰
孙怀辉,姚玉武,产黄峰
(1.合肥学院 生物食品与环境学院,安徽 合肥 230601;2.合肥学院 应用数学与人工智能机理研究重点实验室,安徽 合肥 230601)
在控制工程领域,由Dorato[1]引入的系统的有限时间稳定性(finite-time stability,FTS)得到了越来越多学者的关注。有限时间稳定是指在一段固定时间区间内系统达到期望的性能指标且满足期望的状态轨迹,强调系统响应的瞬时状态行为,在机器人控制、航天飞行器控制、智能制造、材料化工等领域中都有着广泛的应用。Lyapunov稳定性是指当时间趋于无穷时,系统渐近稳定的一种演变状态,强调系统是无限区间内的稳态性能。有限时间稳定性与Lyapunov稳定性的概念是不同且独立的。在实际工程中,尤其是对一些需要做出快速响应的系统,如无人机的姿态控制、机器人轨迹跟踪、反应釜温度控制等[2-3],即使证明了系统状态最终是Lyapunov渐近稳定的,但也可能出现超调量过大或者响应不及时等不良情况,导致系统具有较差的暂态性能,从而无法满足系统期望的性能要求。因此,在控制工程中关于有限时间有界性的研究是十分有意义的[4-8]。随着现代控制理论发展和工具不断的更新迭代,理论的发展需要求解大量的不等式,线性矩阵不等式(LMI)工具箱的引入加快了不等式的求解,使得与有限时间稳定性、有限时间有界性、有限时间跟踪问题的条件易于求得[9]。依据已有的有限时间控制理论研究成果[10-12]可知,有限时间控制的优点在于可改善控制系统的快速收敛性能,从而实现在有限时间内稳定,当系统存在内外部扰动时,相对比Lyapunov渐近稳定的系统具有更好的鲁棒性和抗干扰能力。当考虑具有外部输入的系统时,有限时间稳定性的概念又拓展到了有限时间有界性(finite-time boundedness,FTB)、有限时间有界跟踪等问题上,通常这里的外部输入包括外部扰动以及外部控制率等,由于外部输入使得系统状态在有限时间上的行为更加复杂,使得研究系统在有限时间内的状态更加有意义。
本文采用以下记号,N0表示不包含0的自然数集,Pn表示n维的实欧几里得空间,矩阵P表示矩阵PT的转置,P>0(P<0)表示P是一个对称的正定(负定)矩阵,而P≥0(P≤0)则表示P是一个对称的半正定(负定)矩阵,P≥Q(P≤0)表示P-Q≥0,λmax(A)表示实对称矩阵A的最大特征值,λmin(A)表示实对称矩阵A最小特征值。
1 预备知识
考虑如下的系统
x(k+1)=Ax(k)+f(x(k))ω(k)+Bu(k),
x(0)=x0,y(k)=Cx(k)。
(1)
其中,x(k)∈n是状态向量,A∈n×n、B∈n×q、C∈m×n是系数矩阵u(k)∈q是输入向量,y(k)∈m是输出向量,ω(k)∈p是扰外部动向量,f(x(k))∈n×p是线性或非线性的映射,其中f(x(k))满足:
外部扰动生成的动力方程为:
ω(k+1)=Dω(k),ω(0)=ω0,
(2)
D∈p×p系数矩阵。
假设1对于给定的N∈0,外部扰动满足条件:设系统的跟踪目标r(k)由动力方程(3)生成:
r(k+1)=Gr(k),r(0)=r0,
(3)
其中,参考信号r(k)∈m,G∈m×m是系数矩阵,设Δr(j)=r(j)-r(j-1)。
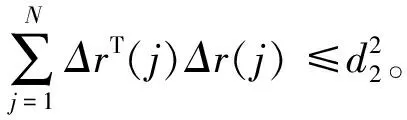
如果满足以下定义[13]:
定义1
其中k∈{1,2,…,N},N≥1,δ>0,d>0,ε>0,R>0。则认为系统(1)和(2)称为关于(δ,d,ε,R,N)是有限时间有界跟踪的。设系统跟踪误差为:e(k)=y(k)-r(k)。
定义2系统(1)和(2)称为对参考信号r(k)关于(δ,d,ε,R,N)是有限时间有界追踪的,如果满足
∀k∈{1,2,…,N},N≥1,δ>0,d>0,ε>0,R>0。
以下是一些重要引理[14]:

引理2设U,V和W是具有适当维数的向量或矩阵,则不等式:UTV+VTU≤UTU+VTV成立。
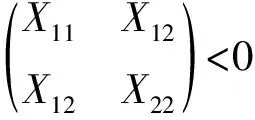
2 主要结论
状态变化量为:
Δx(k+1)=x(k+1)-x(k)
=AΔx(k)+f(x(k))Δω(k)+
Δf(x(k))ω(k-1)+BΔu(k),
(4)
相应的跟踪误差变化量为:
Δe(k+1)=e(k+1)-x(k)=
CΔx(k+1)-Δr(k+1)。
此时注意参考信号变化量Δr(k+1)=r(k+1)-r(k)=Gr(k)-Gr(k-1)=GΔr(k),故有:
e(k+1)=e(k)+CAΔx(k)+
CBΔu(k)+Cf(x(k))Δω(k)+
CΔf(x(k))ω(k-1)-GΔr(k)
(5)
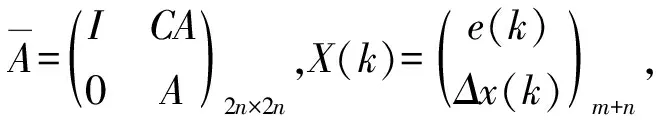
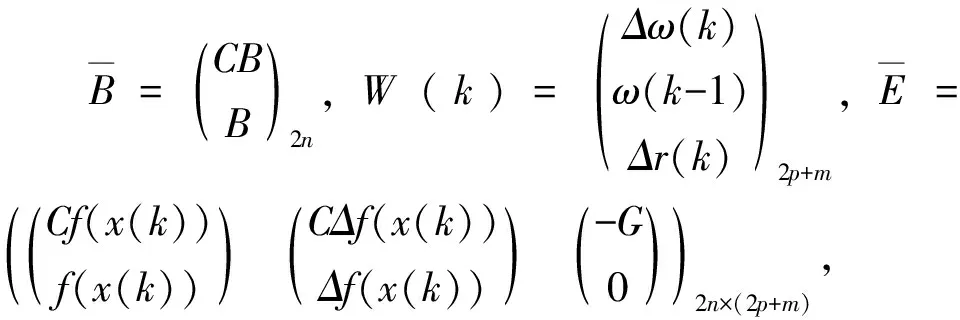
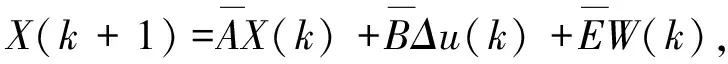
(6)
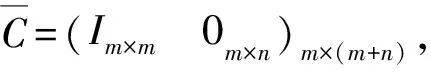
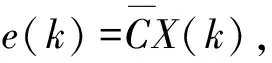
(7)
令其为系统(6)的输出。
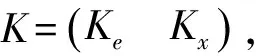
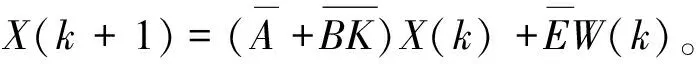
(8)
定理1系统(6)关于(δ,d,ε,R,N)是有限时间有界的,如果对任意给定的数γ>1存在矩阵P1>0,P2>0,使得
(9)
(10)
(11)
其中
证明令V(e(k+1))=e(k+1)P1e(k+1),则由(6)式有
V(e(k+1))=e(k+1)P1e(k+1)=
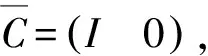
V(e(k+1))≤
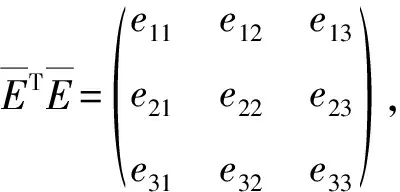
ωT(k-1)e21Δω(k)+ΔrT(k)e31Δω(k)+
ΔωT(k)e12ω(k-1)+ωT(k-1)e22ω(k-1)+
ΔrT(k)e32e12ω(k-1)+ΔωT(k)e13Δr(k)+
ωT(k-1)e23Δr(k)+ΔrT(k)e33Δr(k)。
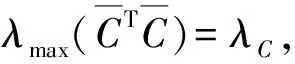
12ωT(k)α2(λC+1)ω(k-1)+
这里设
这样由引理1得到:
由于定理中的条件(9)有
V(e(k+1))≤γV(e(k))+γWT(k)P2W(k)≤
γV(e(k))+γλmax(p2)WT(k)W(k)
(12)
考虑到γ>1,由式(12)可得:
V(e(k))≤γk-1(V(e(1))+
这样,对∀k∈{1,2,…,N},有
V(e(k))≤γN-1(V(e(1))+
由于
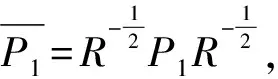
由上面各式有
又对∀k∈{1,2,…,N},由(10)式得
V(e(k))=eT(k)P1e(k)≥
所以
由于定理中的条件(11)即得 eT(k)Re(k)≤ε2。
这样就完成了定理1的证明。
上述定理中,条件(9)、(10)、(11)对于未知矩阵P1,P2来说,各个量之间是非线性的关系,因此验证起来比较麻烦,下面讨论系统(1)和(2)的有限时间有界跟踪问题。为了能利用线性矩阵不等式(LMI)的方法验证结果,取R=I,这也可以考虑是2-范数情况的定理的情形。
令I≤P1≤λ1I,λ2≤P2≤λ3I,由此
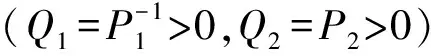
(13)
18α2λ1-γλ2<0,2λ1GTG-γλ2I<0,
(14)
(15)
(16)
证明由定理1中的记号知
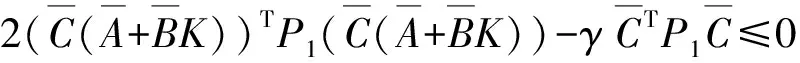
令P1=Q-1,并把前后分别乘以对称矩阵diag(Q1,I)及其转置,并利用引理3可知上式等价于式(13)。
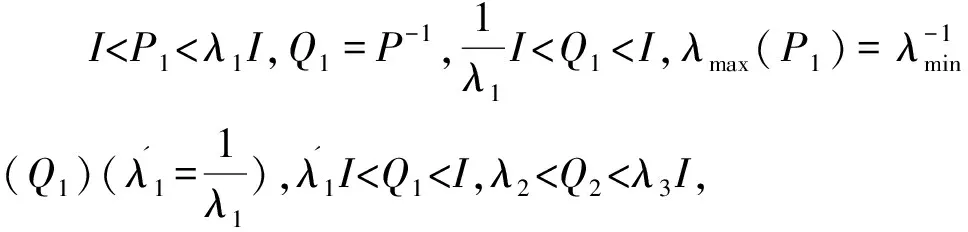
由不等式(11)有
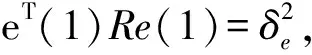
注当系统
x(k+1)=Ax(k)+f(x(x))ω(k)+
Bu(k),x(0)=x0
(17)
其中,f(x(x))=F∈n×n是一个常值矩阵时,式(14)为一个具有外部扰动的线性系统,此时显然满足存在α>0,得λmax(FTF)≤α以应用定理中的充分条件。参考文献[11]给出了一个相应的充分条件。
3 案例模拟
考虑如下的带有外部扰动的单输入单连杆柔性关节机器人系统(其连续情形见文献[4])
x(k+1)=Ax(k)+Bu(k)+
rg((k))LTω(k),y(k)=Cx(k)
式中
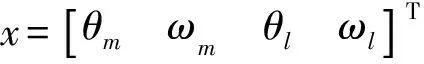
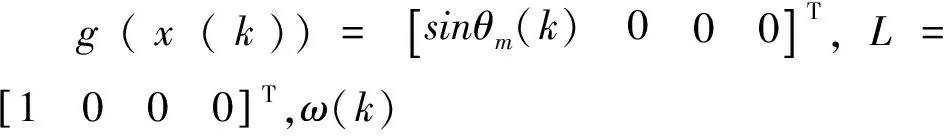
ω(k+1)=Sω(k),

由引理1有:
f(x(k),ω(k))Tf(x(k),ω(k))≤
2x(k)ATAx(k)+2r2ωT(k)LLTω(k)≤
2λmax(τ1I+ATA)xT(k)x(k)+
2r2(τ2I+LLT)ωT(k)ω(k),
这里τ1>0,τ2>0取得适当的值使得τ1I+ATA,τ2I+LLT是正定的对称矩阵。
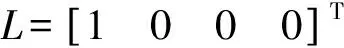
这样就得到:
f(x(k),ω(k))Tf(x(k),ω(k))≤
xT(k)R1x(k)+ωT(k)R2ω(k)=
2.9528IxT(k)x(k)+2.02r2IωT(k)ω(k)。
因此向量值函数f(x(k),ω(k))满足条件,此时Q=I,R1=2.9528I,R2=2.02I2。取r=-0.0007,γ=25,利用线性矩阵不等式LMI工具箱求解(9)-(13)可得λ1=3.7148,λ2=56.5871,λ3=167.1860,Q1=0.9995I,Q2=111.5457I,
由定理2可知系统关于(δe,d1,d2,ε,R,N)=(0.01,0.001901,0.002,0.01,I,6)是有限时间有界追踪的。
图1中显示了所给的非线性系统状态分量x1(k),x2(k),x3(k),x4(k),给定初始x1(k)=-10,x2(k)=-20,x3(k)=-30,x4(k)=-40,可以看出案例中闭环离散系统状态随着时间能够较好地收敛,从而有效地验证了前面定理中所给条件的可行性。
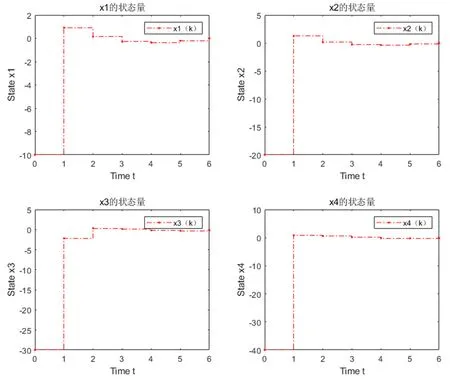
图1 x的状态分量
4 总结
本文研究了一类具有外部扰动的非线性系统,通过对所构造的新系统的有限时间有界性来讨论其有限时间有界跟踪问题,得到了这类非线性系统有限时间有界跟踪的充分条件,这些条件能较为有效地判别系统的状态在有限的时间段上的运行情况。最后,数字仿真也可以看出关于这类非线性系统的有限时间有界跟踪的结论是可行的。
