云制造环境下的两级多任务调度
2023-10-26尹向兵
尹向兵,周 婷
(1.安徽警官职业学院 教务处,安徽 合肥 230031;2.安徽城市管理职业学院 商贸管理学院,安徽 合肥 230011)
随着全球制造业的发展,云制造模式备受关注。云制造平台作为云制造系统体系结构的一个重要组成部分,聚合了不同供应商所提供的分布式资源[1],并对它们进行集中式规划管理,从而为客户提供最佳的云服务[2-3]。然而,在大多数情况下,由客户所提交上来的任务是十分复杂的,它们必须被分解为多个子任务,再由聚合的分布式资源进行处理。而分解后的子任务之间往往具有复杂的优先级关系。同时,受不同资源能力的限制,并不是每个在平台上注册的资源都能满足各种任务请求。因此,如何调度多个任务以及如何在考虑优先级约束和资源服务资格的情况下调度所有必要的子任务,是云制造中一个困难且重要的问题。
迄今为止,已经有许多研究人员对云制造中的调度问题进行了研究,但只有少数人关注多任务的调度。而大规模定制会有多种多样的需求,因此,关注异构多任务的调度更为实际、更为合理。先前的大部分相关工作都将多任务分解后的所有子任务视为相同的任务,并在它们之间进行无差别调度。这样做可能导致单个任务需要花费很长时间才能完成。除此之外,需要完成的任务不止一项,并且不同任务之间可能存在利益冲突。因此,与其最小化某个任务的最大完工时间,不如最小化所有任务的平均完工时间。同时,从云制造平台的角度来看,所有的请求也应该尽快完成,这样,相关的资源服务不仅能得到高效利用,还有机会对即将到来的新任务集进行快速响应。所以,多个任务的总完成时间也应该最小化。
基于上述思路,本文提出了一种新的两级调度模型,用于处理提交给平台的多个任务调度请求。该模型包括任务级和子任务级调度,其目标是在考虑优先级约束和资源能力约束的情况下,最小化每个复杂任务请求的最大完工时间。针对所提出的两级调度模型,设计了两种不同的解决方案进行比较,即两级一优化调度(two-level-one-optimization scheduling,TLOOS)和两级二优化调度(two-level-two-optimization scheduling,TLTOS)。这两种方案都采用了Liao等[4]提出的有效改进蚁群算法并应用于子任务的调度。具体来说,TLOOS方法根据“先进先出”规则对多个任务进行排序,而TLTOS策略则是寻找一个接近最优的任务序列,目标是最小化所有请求的总完成时间。为了评估所提出的模型和解决方案的优点,随后对随机生成的数据进行了大量计算实验。
1 相关工作
近年来,有关人员研究了云制造环境中的调度相关问题。许多研究从不同的角度处理调度问题,本文从任务数量、任务特征、调度方法、调度目标和优化方法等角度对各项工作进行了总结。
对于多个复杂任务的调度已经研究了很多年。为了解决云设计资源调度问题,文献[5]设计了一个调度模型,并通过遗传算法实现。该算法使用了线性加权多目标定义的适应度函数,以最小化成本和时间并最大化服务质量。文献[6]在考虑任务优先级约束和资源限制的情况下,开发了一种改进的遗传算法,用于调度云制造中的多个简单任务,目标是最小化最大完工时间。
上述所有论文的优化方法都是基于单一目标或者将多目标转化为单一目标。其他一些研究则关注多目标优化。文献[7]建立了一个基于云的拆卸系统的数学模型,该系统为多个请求提供拆卸服务,并应用多目标遗传算法,以最小化总完工时间和总成本两个优化目标来求解该模型。文献[8]提出了一种多目标优化调度模型以提高可重构装配线的生产效率,并采用基于距离排序粒子群优化的有效方法对该模型进行求解,其目标是将装配线改造成本降至最低,实现生产负荷均衡,并最大限度地减少工作量的延迟。
为了克服单独优化整个系统的局限性,文献[9]提出了面向多任务的一个云制造服务组合与调度模型,该模型考虑了云制造的关键因素,如服务导向、物流参与和服务可用性的动态变化。文献[10]建立了一个多任务调度模型,并用以客户为中心的方法和综合方法等不同的设计视角进行求解。
上述文献中提出的任务调度策略都是集中式的。为了实现实时数据驱动的调度,文献[11]提出了一种基于博弈论的云制造柔性作业车间调度问题的动态优化模型。与集中式调度策略不同,该模型中的每台机器都是一个活动实体,在考虑最小化负载指数和最大化利用率的情况下,请求处理任务以使其收益最大化。文献[12]提出了一个支持RFID的实时制造执行系统,可以为计划和调度决策提供实时数据。实时调度策略可以极大地消除调度与执行之间的偏差,但需要依靠实时数据,因此,实时调度并非总是可用的。基于以上情况,本文遵循集中式调度策略。
2 问题描述
考虑在调度期开始时提交给云制造平台的n个任务。这n个任务根据接收到的顺序被标记为T={T1,T2…Tn}。令w={w1,w2…wn}表示所有任务的工作负载集,即每个任务的数量。任务i可以分解为im个子任务,即Ti={ti1,ti2…tim}。对于每项任务,分解后的子任务的依赖关系不是简单的序列结构,而是并行和序列结构的结合。此外,每个子任务只能由可用服务的子集来完成,具体可由式(1)来形式化描述。ESij(k)表示服务k对于任务i的子任务j的资格,当它等于1时,意味着服务k可以完成任务i的子任务j。
(1)
如上所述,不同的任务在子任务之间具有不同的优先级关系,其约束形式可以表示为式(2)。RCjl表示子任务j和子任务l之间的关系约束。
(2)
影响每个子任务完成时间的因素有三种,即处理时间、设置时间和传输时间。处理时间是所选服务执行每单位工作负载的某个子任务所花费的时间。如果任务i中的子任务j被安排在服务k上,那么单位工作负载的处理时间可以表示为Pij(k)。因此,总处理时间为PTij(k)=Pij(k)*wi。设置时间是指服务准备处理子任务的时间。传输时间指将已完成的先前子任务转移到所选服务所在位置,以执行后续子任务所需的时间,包括打包、文档和运输时间。假设服务始终可用,则服务k上任务i的子任务j的预测开始时间,即PSTij(k)可以用式(3)表示:
(3)
其中mn(k)指服务k在tij之前执行的任务tmn。因此,STmn(k)ij(k)表示在服务k上从执行任务tmn到tij的设置时间。服务k和服务g应遵循等式(4)中的约束。这意味着服务k应该完成子任务tmn和子任务tij,而服务g应该完成子任务til。
ESil(g)=ESij(k)=ESmn(k)=1
(4)
如果在服务k上的tij之前没有执行任务,则STmn(k)ij(k)=ST0ij(k),表示服务k上的tij的初始设置时间。FTil(g)是服务g处理的前一个子任务til的完成时间,其中,l∈preij,其中preij表示子任务tij的前一个子任务的集合,可以通过preij={l|l∈RCjl=1}获得。TTil(g)ij(k)是将服务g执行的任务til转移到服务k执行的任务tij所需的时间。如果服务g和k都由同一家企业提供,则TTil(g)ij(k)为零。
事实上,从任务i分解出来的子任务j的实际开始时间还取决于所选服务k的可用时间ATij(k),即服务k可用于处理当前请求的最早时间。因此,资源k处理任务i的子任务j的实际开始时间和结束时间(分别表示为ASTij(k)和FTij(k))计算如式(5)(6):
ASTij(k)=max(PSTij(k),ATij(k))
(5)
FTij(k)=ASTij(k)+PTij(k)
(6)
目标函数可以从完工时间、延误成本和资源利用率等多个方面以不同的方式定义。本文采用的性能标准是最大完工时间,包括以下两种:单个任务的最大完工时间和总任务的最大完工时间。
对于单个任务i,目标是最小化其所有子任务的最大完成时间,该时间可通过公式(7)计算,其中ASij(k)∈{ES|ESij(k)=1}。这意味着处理任务i的子任务j的实际服务k(用ASij(k)表示)属于使ESij(k)等于1的集合。在式(7)中,i是一个从任务集T中选择的任务。
(i=T1,T2,…,Tn)
(7)
从云制造平台的角度来看,调度目标是找到一个完成所有任务的时间最短的方案,具体如式(8):
(8)
除了(1)和(2),优化还受到附加约束,如式(9):
(9)
如果Prijcdk=1,FTij(k)≤ASTcd(k)
(10)
(11)
约束(9)意味着每个子任务应该只分配给一个合格的服务。在约束(10)中,Prijcdk=1表示任务i的子任务j被安排在任务c的子任务d之前的服务k上。约束(10)确保服务在任何给定时间只能执行任务的一个子任务。约束(11)表示并非所有服务都能满足任何请求,即对每个服务都有资格限制。
3 方法设计
3.1 一级调度方法
一级调度,也称为一级优化调度(one-level-one-optimization scheduling,OLOOS),即对所有任务分解得到的子任务在不违反优先级关系的前提下进行无差别调度。在为子任务选择服务时,必须考虑资源的资格,并非所有资源都可以用于每个子任务。子任务级调度被用作一级调度方案,其目标是在不考虑每个单独任务完成时间的情况下尽早完成所有子任务。一级调度的目标函数如式(8)所示,这表示最小化所有任务的总完成时间。本文成功地验证了蚁群算法ACO4STLS(ant colony optimization for subtask-level scheduling)在确定一级调度最优解方面的有效性(具体细节见3.3节)。
3.2 两级调度方法
本文提出的两级多任务调度方法包括任务级调度和子任务级调度。两级调度包括三个部分:所有任务的排序、每个任务子任务的资源选择和子任务的排序。任务级调度涉及第一部分,后两部分由子任务级调度处理,不违反与每个任务相关的子任务的优先级约束和服务资格。
根据该模型,多个任务的顺序起着重要作用。因此,在上层,本文考虑了两种任务级调度方法。第一种方法根据简单的“先进先出”规则对所有任务进行排序。而为了探索更好的序列,以实现更短的总完工时间,第二种方法使用了ACO4TLS(ant colony optimization for task-level scheduling)算法进行任务级调度,将在3.3节中具体介绍。ACO4TLS算法能够有效地分配每个任务的处理顺序,目标是根据等式(8)最小化总完工时间。
基于本文提出的任务级和子任务级调度方法,得到了两级多任务调度方法:两级一优化调度(TLOOS)方法和两级二优化调度(TLTOS)方法。
结合一级调度方法和两级调度方法,上述三种调度方法的示意图如图1所示。具体地说,对于OLOOS,优化目标是最小化整体完工时间,如式(8)所示。对于TLOOS方法,优化目标是根据式(7)最小化每个单独任务的完工时间,总完工时间是所有任务中的最大完工时间。另外,对于TLTOS,上层调度的优化目标是最小化式(8)中所示的整体完工时间,而下层调度的目标是最小化式(7)中每个单独任务的完工时间。

图1 三种调度方法的框架
3.3 ACO4STLS和ACO4TLS
3.3.1 ACO4STLS
ACO4STLS算法是一种用于一级调度和二级调度下层的子任务调度方案。ACO4STLS算法基于文献[3]中提出的改进ACO算法(IACO)。IACO是一个依赖于两个向量的两阶段调度过程。第一个向量称为分配向量,其大小与要调度的子任务数相同。因此,向量大小是一级调度中所有任务的子任务数,而向量大小等于两级调度中与被调度任务相关联的子任务数。向量中的每个值表示分配给所选子任务的服务。第二个向量是子任务序列排列的向量,它也具有相同大小的子任务。为了得到可行的调度方案,需要两个用于服务分配和子任务排序的概率矩阵。对于服务分配过程,服务k被分配到任务i的子任务j的概率矩阵如式(12)所示:
(12)
其中
(13)
其中,PTij(k)是服务k执行任务i的子任务j的处理时间。
对于子任务排序的步骤,子任务j将在子任务i确定后安排,如式(14):
(14)

上述两个概率矩阵中的信息素矩阵更新如式(15):
(15)
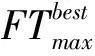
如前所述,属于同一任务的子任务具有优先约束。因此,子任务序列应该符合优先约束。如果违反了优先约束,则需要调整顺序。ACO4STLS算法在一级调度方法中只调用一次,但调用次数与TLOOS方法中的任务数相同。
3.3.2 ACO4TLS
ACO4TLS用于TLTOS的上层调度。ACO4TLS与ACO4STL类似,但在以下方面有所不同。首先,如前所述,它们在目标函数上有所不同。其次,ACO4TLS中的候选解决方案是将一系列任务用向量表示,这与ACO4STLS中使用的第二个向量类似。然而,两个向量的大小很可能不同。第三,ACO4TLS与ACO4STL排序部分的不同之处在于信息素矩阵和启发式信息矩阵的更新方式。在ACO4TLS中,从任务i到任务j的信息素由以下等式更新:
τij(itr+1)=(1-ρ)τij(itr)+Δτij
(16)
式中,itr是迭代次数。Δτij的计算如式(17):
(17)
其中M是蚂蚁的数量,Q是一个常数(在本文中设置为1),TMm是目前为止由蚂蚁m构造的序列的最大完工时间。与经典的旅行商问题不同,任何一对任务之间都没有明显的启发式信息。因此,将启发式信息矩阵设置为单位矩阵。最后,与ACO4STL中的子任务排序不同,ACO4TLS中的任务排序没有优先级约束问题。TLTOS方法只是ACO4TLS和ACO4STL的组合。
4 实例分析
4.1 数据生成
为了评估和比较不同的多任务调度方法,生成数据,通过改变服务数量、任务数量和每个任务的子任务数量来模拟不同规模的问题。服务的数量取三个值:4、8和12。可以选择每个服务来执行多个子任务。任务的数量在三个级别上选取:4、8和12,而子任务的数量在8、10和12上有所不同。因此,总共可以形成33=27个问题大小的组合。受正交实验设计的数据选择策略的启发,从这27个组合中选择了9个,即4s4t8st、4s8t10st、4s12t12st、8s4t10st、8s8t12st、8s12t8st、12s4t12st、12s8t8st、12s12t10st,以测试不同调度算法的有效性和效率。此外,表1总结了生成数据集的处理时间、设置时间、传输时间和工作负载的范围。

表1 不同数据集的时间和工作负载范围
4.2 蚁群算法参数
表2给出了子任务级调度中使用的ACO4STLS算法的参数,以及任务级调度中使用的ACO4TLS算法的参数。[·]是整数运算。具体来说,对于两级多任务调度,将蚂蚁的数量设置为与每次调用ACO4STLS算法时的子任务数|ST|成正比,即|ST|等于任务i的子任务数,即当前正在考虑的任务。另外,对于一级多任务调度,ST是所有任务的所有子任务集合。T的基数|T|等于调用ACO4TLS算法时要调度的任务数。对于每个问题,每个调度方法重复运行10次,以获得关于最优解质量的统计信息。

表2 不同方案中使用的ACO算法的参数
4.3 实验结果及分析
测试结果从两个角度组织和呈现:单个任务的最大完工时间和所有任务的总完工时间。从单个任务的完工时间的角度出发,分别计算了10次运行期间所有任务完工时间的平均值和标准偏差。由于每个数据集中都包含多个任务,因此,在每次运行中都会计算所有单个任务的最大完工时间的平均值和标准偏差。表3总结了不同调度方法的测试结果。从表3可以看出:
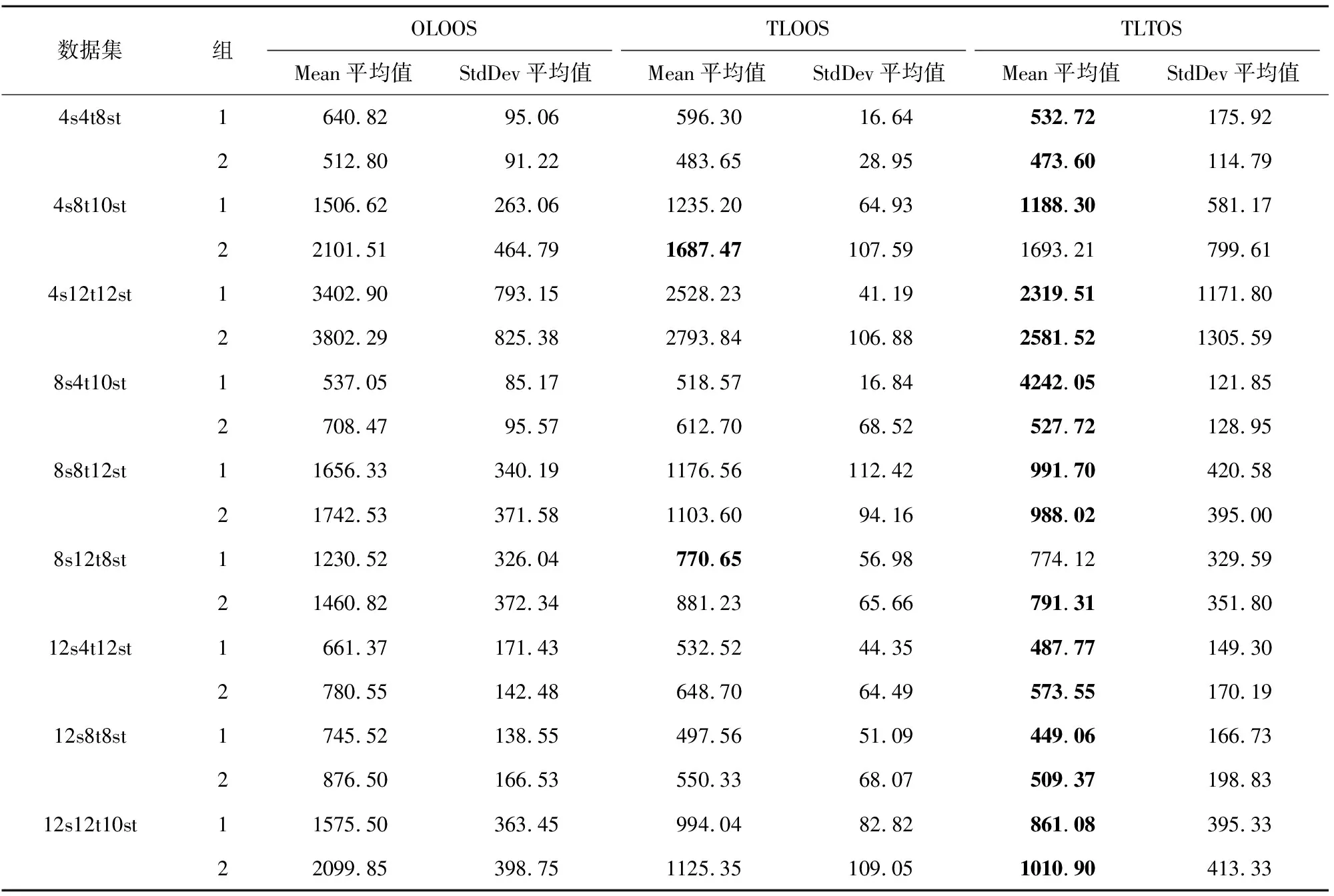
表3 不同调度方案得到的单个任务完工时间的均值和标准差的平均值
(1)两级调度方法TLOOS、TLTOS在所有情况下都优于OLOOS;
(2)在所有18个测试数据集中,TLTOS在16个数据集中得到低于TLOOS的平均值(以粗体突出显示),而TLOOS在2个数据集中得到低于TLTOS的平均值。因此,TLTOS明显优于TLOOS。
从平台的角度来看,如果一批计划的所有任务都可以尽早完成,那么被调用的服务可以更快地开始处理下一批任务。因此,总任务的完成时间也非常重要。为了从平台的角度比较不同调度方案的性能,在每次运行中计算完成每个仿真案例中所有任务的总完工时间。表4总结了批量完成10次以上的所有任务的最大完工时间的平均值和标准偏差。结果表明:
(1)当服务和任务数量较少时,TLOOS未能获得比OLOOS和TLTOS更好的时效;
(2)当服务的数量较大时,TLTOS在整体完工时间上优于其他两个方案;
(3)上述观察结果适用于从不同值范围生成的两组数据,这意味着性能差异主要来自调度方案本身,对数据生成不敏感。
图2显示了三种方案在处理所选数据集(即组1的8s4t10st)时的收敛过程。对于每个调度方案,描绘了两个收敛曲线:一个是所有单个任务完成时间的平均值,另一个是所有重复测试的总完成时间的平均值。结果表明:
(1)无论从整体完工时间还是单个完工时间的角度来看,所提出的两级调度模型在大多数情况下都优于一级调度模型;
(2)TLTOS的收敛速度低于TLOOS;
(3)所有配置文件都会收敛,表明设置的停止运行的迭代次数是足够的。
总之,TLTOS不仅在最小化单个任务的最大完工时间方面优于其他两种调度方法,而且在最小化被调度的整批任务的最大完工时间方面也优于其他两种调度方法。然而,TLTOS的这种优异性是以计算时间为代价的。TLTOS的复杂度高于其他两种方法,这从表5所示的CPU时间可以看出。可以观察到,在三种调度方案中,TLOOS占用的时间最短,而TLTOS占用的CPU时间最长。因此,对于希望以较低计算质量为代价获得快速响应的请求,TLOOS方法相比于其他调度模式是更好的选择。然而,在复杂的制造要求需要很长时间才能完成的情况下,缩短完工时间比增加CPU时间带来的惩罚更重要。因此,在云制造环境中,使用TLTOS来寻找一个更好的、时间更短的时间表来调度多个复杂的请求是有意义的。
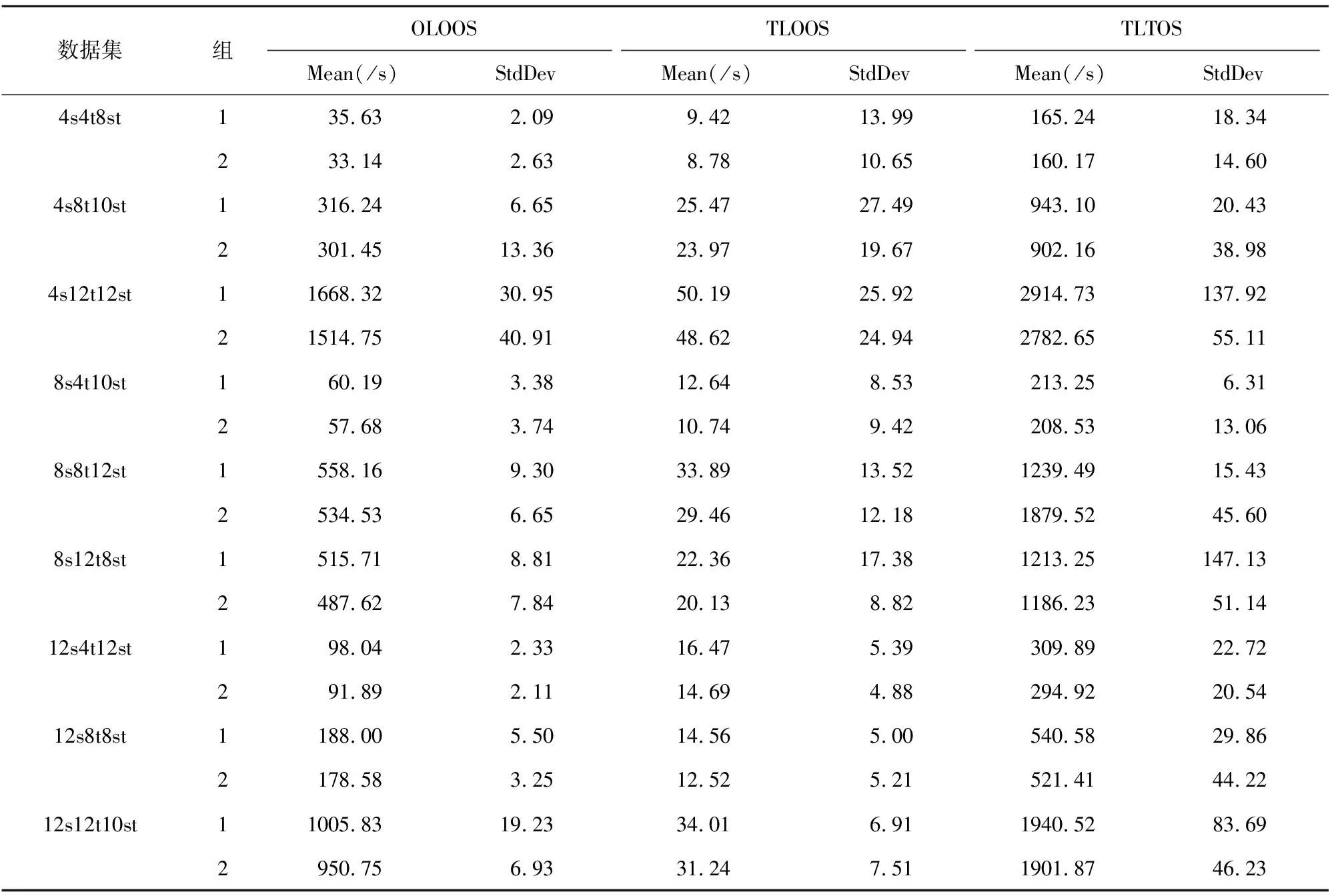
表5 不同调度方案对应的CPU时间的均值和标准差
5 结语
本文提出了一种新的两级调度模型,在考虑子任务优先约束和资源服务资格的情况下,描述了云制造环境下的多任务调度问题。基于该模型,提出了两种新的两级调度优化方法,即两级一优化方法和两级二优化方法。为了验证所提出的模型和求解方法的有效性,将其与常用的一级调度模型和求解方法进行了比较。针对时间目标,基于随机生成的不同规模的数据集进行了计算实验。试验结果表明,所提出的两级调度模型在单个任务的最大完工时间以及所有任务的完工时间方面优于一级调度模型,所提出的两级二优化调度方法也优于其他两种优化方案。
