基于Hessian矩阵和LBF模型的指静脉图像分割

杨罗坤,张 浩*,方 畅,叶明全,3,毕迎春

(1.皖南医学院 医学信息学院,安徽 芜湖 241002;2.皖南医学院附属弋矶山医院,安徽 芜湖 241004;3.网络与信息安全安徽省重点实验室,安徽 芜湖 241003)

互联网技术快速发展的同时也伴随着网络盗窃案件的层出不穷,使得人们越来越重视个人的隐私安全。生物识别技术通过计算机结合数学、物理、生物、医学等学科,利用人体自身的生理特征来完成个人身份的认证,是隐私保护的重要手段。传统生物识别所用的生理特性包括指纹、人脸、虹膜和指静脉等。其中指纹、人脸具有易采集、成本低的优势,但存在易磨损、伪造和隐私问题[1];虹膜则具有识别率高、难伪造的特点,但存在成本高、可接受性低的问题。近年来,指静脉研究受到越来越多的关注,该生理特性既具备易采集和难伪造的特点,又具有较好的隐私性。目前,指静脉识别技术正处于飞速发展阶段,具有广泛的发展空间和研究价值。

指静脉图像由红外摄像头拍摄获取,图像质量受到光照、采集者自身条件的约束,相较于指纹、人脸等图像,对比度明显降低。图像分割技术是图像预处理阶段的重要步骤,对图像识别率的提高起到关键作用[2]。传统的阈值分割[3-4]和最大曲率分割[5]对血管边缘与背景的对比度非常敏感,不能很好地区分静脉血管和图像背景的边界。基于Gabor滤波和LBP纹理提取的指静脉分割算法相较于原始LBP方法提高了分割的准确率和识别率[6],但同时也降低了分割效率。李凡等[7]运用图像金字塔和NiBlack方法提取静脉特征,可得到对比度清晰的指静脉细化图,然而这种方法在处理模糊图像时会产生较多的伪静脉纹路。Yao等[8]提出一种RLF(radon-like features)的指静脉特征提取方法,该方法通过计算指静脉图像中每个像素的平均曲率实现对指静脉图像的处理。林剑等[9]利用高斯滤波器的二阶导数与图像卷积得到Hessian矩阵,再基于实对称矩阵的特点提取静脉图像,并通过调整滤波器窗口半径得到最佳效果。Jong等[10]提出一种基于对比度受限的自适应直方图均衡化的指静脉分割方法,但该方法对于边缘模糊的图片分割效果不佳。蓝师伟等[11]提出融合静脉曲率特征、曲率细线特征和背景曲率灰度特征的方法,进一步优化了图像提取和识别的性能。王保生等[12]利用Gabor滤波和水平集方法对指静脉图像进行分割,得到了较好的分割精度,但对于低质量图像,曲线的演化很难完全包裹静脉边缘。Khamis等[13]提出了以模糊直方图均衡化为中心的增强阶段集,该方法完善了一套具有低计算复杂度和高分辨能力的指静脉增强技术。Zhang等[14]将卷积神经网络与Gabor滤波器相结合,基于目标函数计算Gabor滤波器参数的梯度,通过反向传播对其参数进行优化,得到较好的增强效果,但此方法难以区分低对比度的指静脉图像。

综上所述,国内外专家学者在指静脉的分割和图像增强方面已进行了较多研究,但在低对比度、边缘信息模糊图像的处理上仍存在较多的不足之处。手指静脉纹路总体呈线状结构且静脉宽度不同,基于Hessian矩阵的方法被广泛应用于血管类图像的增强。文中将基于手指静脉特点,利用Hessian矩阵增强手指静脉结构,同时对血管响应函数进行改进,提高手指静脉和背景区域的对比度。对增强后的图像利用LBF(Local Binary Fitting,局部二值拟合)模型提取手指静脉纹路,通过对阈值τ的判断去除静脉纹路中孤立和间断部分,最后将图像进行细化操作得到最终的手指静脉骨架。与原始的图像相比,该方法可得到脉络特征明显、分割清晰的静脉图像。另外,文中的方法对处理边缘模糊、对比度低的静脉图像也有很好的效果。

1 指静脉图像预处理

由于原始指静脉数据集中存在若干边界和背景区域。需对图像进行ROI区域提取,获取指静脉区域信息。研究运用Canny算子提取出手指轮廓,得到较为清晰的手指轮廓图像。由于测试者的手指粗细与弯曲程度差别较大,单纯按照手指轮廓线提取的图片形状、大小也各不相同,很难统一。通过分析发现,可以将手指形状近似地看成矩形,并基于该形态学特性提取统一的图像。

通过对数据集的整理发现,手指轮廓横向整体位置趋于图像中心。此时以中心线为对称轴,从左至右依次扫描整个图像,分别沿线(X,Y0)向上、下寻找第一个像素值为255的点坐标,将上下移动的距离之和相加,作为当前手指宽度。扫描完成后,将宽度的最小值作为提取矩形的宽度。为防止部分图像手指轮廓内部因出现噪点导致距离过小,设置阈值M,若距离小于M则继续向上移动。

统计所有图像的宽度,得到宽度的区间范围。分析发现宽度集中在100～110之间。根据原始图像轮廓边缘几乎没有静脉信息的特点,取矩形宽度为100。图1为最终确定的ROI图像。

图1 指静脉ROI区域

2 基于Hessian矩阵的指静脉图像增强策略

Hessian矩阵常用于牛顿法解决优化问题,可被用于判定多元函数的极值问题,因此也常被用于血管图像的增强。

2.1 Hessian矩阵的基本原理

(1)

将式(1)写成矩阵的形式,得到:

(2)

其中,令:

(3)

式(3)为f(x1,x2)在X(0)点的Hessian矩阵。

2.2 基于Hessian矩阵的指静脉图像增强算法

低精度、低对比度的图像是影响图像识别率的主要原因。对指静脉图像进行增强操作主要是对静脉脉络进行增强,增加图像的对比度,为下一步的特征识别做铺垫。Hessian矩阵的表示形式如式(4),它是由图像在水平区域、垂直区域和对角上的二阶偏导组成的方阵。通过对矩阵的特征值进行分析,可以预测区域内是否有静脉血管出现。

(4)

式(4)中fxx、fdx、fyx、fyy表示图像在不同方向的二阶偏导数。f(x,y)是当前图像的灰度值,那么f(x+1,y+1)表示f(x,y)在3×3的邻域像素区域的灰度值。由尺度空间理论可知,图像的二阶导数可以通过高斯函数的二阶导数与原图像卷积得到,因此在计算Hessian矩阵时一般使用公式(5):

(5)

其中,G(x,y;σ)为高斯函数,σ为标准差,也称尺度因子。具体对图像进行处理时,一般选取窗口半径为3σ,实验证明,尺度因子越接近静脉宽度,静脉显示效果越好。

对于图像中的某一个像素而言,它的Hessian矩阵是2×2的规模,所以一定存在两个特征值(重根算重数)。通过对图像进行卷积操作,得到两个特征值λ1、λ2和与其相关的特征向量v1、v2,不妨设|λ1|≤|λ2|。由于v1和v2相互垂直,对于检测到的静脉区域,ν2垂直于静脉方向,静脉图像在该处灰度变化大。ν1平行于静脉方向,静脉图像在该处灰度变化较小。根据特征值大小可以判断静脉的线状结构,如表1所示:

表1 特征值和对应的结构

Hessian矩阵的特征值和相关的特征向量分别代表该点沿某一方向上的曲率大小和方向。λ2表示曲率变化较大的方向,λ1表示曲率变化较小的方向。对于处于指静脉血管位置的像素点,设特征值λ2的绝对值较大,它所对应的特征向量ν2与血管方向垂直,此处血管边缘的灰度值变化明显;特征值λ1的绝对值较小,它所对应的特征向量ν1与血管方向平行,灰度值变化非常小。根据图像形态把图像中的像素大致分为三类:

(1)背景:它们的灰度分布较均匀,任意方向上灰度变化都较小。

(2)孤立的点、角点:它在任意方向上的灰度变化都很大。

(3)血管:获取的图像中,血管沿径向方向λ2上的灰度变化始终较大,轴向方向λ1上的灰度变化较小。

通过对λ1、λ2的特征值进行判断,可以将背景、孤立的点以及血管分割出来。研究中所使用的二维手指静脉图像背景灰度值高于手指静脉区域灰度值,手指静脉区域在图像中为暗线结构。

2.3 Hessian矩阵的指静脉图像增强算法的优化

通过2.2节的分析,对λ1、λ2的特征值进行判断,可以将背景、孤立的点以及血管分割出来。研究中手指静脉区域为暗线结构,如图2所示。

图2 指静脉原始图像

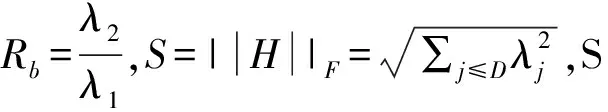
(6)

表2 λ1、λ2值图像区分对照表

从表2可以看出,A对孤立点有抑制作用,B对背景有抑制作用,只有血管处的信号响应强烈。式(6)中β、γ为阈值系数,β用于对图像中块状和条状区域的敏感程度进行调节。如果β很大,A趋近于1,对孤立位置的抑制就会降低;当β很小时,A容易受到Rb的影响趋近于0,在血管弯曲处,孤立点也容易受到抑制。系数γ用于对图像的平滑程度进行控制。S的变化影响函数对血管处的响应,如果γ变大,S的变化减弱,图像就变得平滑。γ很小,把S放大,那么滤波后的图像就变得上下浮动较大。

由于Hessian矩阵和血管响应函数与特征值的平方成正比,主要是为了抑制低对比度和不均匀区域的噪声,这些区域的特征值较小。但在实际图像中,静脉血管特征值的分布并不均匀,它在静脉的中心位置达到最大,接着沿截面方向往边缘依次递减,在静脉交叉位置和弯曲部位的响应较差,在对比度低的图像中灰度值无明显变化。如图2所示,原始的图像中静脉信息相对模糊,图像灰度不明显。针对这种缺陷,对式(6)中血管响应函数进行优化,提高血管增强效果。为了保证增强函数对于低特征值的健壮性,对特征值的系数做出相应改进。改进后的响应函数如式(7)所示。经过实验证明,当特征系数为特征值绝对值的二次方时,效果最佳。如图3所示,改进响应函数后的图像对比度比原响应函数的图像高。

图3 改进响应函数前后的增强效果对比图

V(p)=f(x)=

(7)

3 基于LBF模型的图像分割算法

指静脉图像经过Hessian矩阵的增强后,静脉血管和背景的对比度更加明显,在Hessian矩阵增强的基础上,运用LBF算法来提取手指静脉纹路。LBF模型是一种基于可变区域的能量泛函模型,运用于分割不均匀的图像。初始轮廓的选取对LBF模型的影响较大,且对于一些具有弱边界的医学图像处理的效果不佳。LI等[15]人提出LBF模型,设给定的图像为I:Ω∈Rd,Ω表示图像域,d表示表示图像维数,C表示图像上的轮廓线,故LBF模型的能量泛函为:

(8)

式(8)中,λ1和λ2为拟合项系数,in(C)和out(C)是曲线C所围的内外部区域,f1(x),和f2(x)是在点x处图像的灰度拟合值。其中:

引入水平集函数φ,in(C)对应{x∈Ω,φ(x)>0},out(C)对应{x∈Ω,φ(x)<0},引入Heaviside和Dirac函数进行区域划分,重新书写LBF模型的能量函数,如式(9):

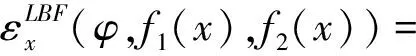
(9)

运用Hessian矩阵增强手指静脉结构,对增强后的图像使用LBF算法提取手指静脉纹路。将Hessian矩阵增强算法与LBF模型结合使用,完成对图像的分割。

4 实验结果和分析

4.1 实验环境

实验数据集采用SDUMLA-HMT手指静脉图像,经处理后的图像大小为100×260像素,通过Matlab在Windows10,Core i5-8400,8G内存环境下进行实验。

4.2 基于Hessian矩阵与LBF模型的指静脉图像分割结果

4.2.1 对普通指静脉图像的处理

由图4(c)和(d)可知,改进后响应函数在静脉区域亮度和静脉结构的连续性的增强效果上均优于原始响应函数。图4(c)中存在多处静脉区域边缘与背景分界不明显,同时有很多的间断区域;图4(e)显示出图像经原始响应函数增强后,使用LBF模型分割,出现了多处错误边界;图4(f)显示出经改进响应函数增强后使用LBF模型分割,曲线基本正确覆盖静脉区域边界。接着将图像进行二值化处理,如图4(g)和(h),通过计算白色连通区域的面积,选取阈值τ=60,将低于该面积的部分去除,如图4(i)和(j),经细化后得到最终的手指静脉骨架。对比图4(k)和(l)可以看出,图4(l)在静脉骨架的完整性和连续性上明显优于图4(k)。

图4 基于Hessian矩阵与LBF指静脉分割效果图

4.2.2 对模糊指静脉图像的处理

图5(a)与图4(a)相比,图像质量明显下降,静脉边缘与背景区分度较低,存在多处大面积的模糊区域。从图5(b)可以看出,使用原始LBF模型,不能很好地将静脉血管区域分割出来。使用文中的方法对图像进行增强后虽然出现了部分间断和孤立点,但整体结构仍与原始图像较为符合,如图5(d)所示。而图5(c)使用原始响应函数增强的效果对比度很低,静脉边缘与背景分离度不高,在使用LBF模型时,由于图5(c)的增强效果不明显,导致曲线演化过程无法清晰地与静脉边缘拟合。图5(e)中几乎整个黑色背景被认为是内部区域,进而造成在二值化过程中将大部分背景区域划分为静脉区域,如图5(g),最终的细化结果也无法反映原图真实的静脉纹路,如图5(k)。而图5(l)的静脉骨架虽由于原始图像的模糊问题也出现了一定的间断,但在整体结构上仍符合原图像。

图5 模糊图片基于Hessian矩阵与LBF指静脉分割效果图

5 结语

本文针对模糊手指静脉图像分割展开研究,提出基于Hessian矩阵和LBF模型结合的指静脉图像分割方法。利用Hessian矩阵和指静脉结构的线性特征,通过对血管响应函数的改进,并结合LBF模型获取静脉主要轮廓。通过图像二值化、剔除孤立点和细化操作,最终得到手指静脉骨架图。实验结果表明使用文中方法得到的最终骨架图,在整体结构和连续性上均优于原始方法。