传统法有条不紊 高观点扶摇直上
——谈2023年唐山一模第22题一题多解以及命题手法
2023-10-26唐洵
唐 洵
(福建省福清第三中学,福建 福清 350000)
高考或质检中的导数证明问题,其求解过程一般是利用导数工具分析函数的性质,进而得到问题的答案.此类解法虽然步步为营,但过程往往错综复杂,一招不慎,满盘皆输.因此在解题时,若能充分挖掘表达式的代数结构,联想几何特征,再融入一些高等数学的观点,势必能速战速决,蹑影追风.
1 题目呈现
题目(2023年唐山3月一模)已知x>-1,证明:(ex-1)ln(x+1)≥x2.
2 解法展示
思路1整体构造,一马平川.

令g(x)=x2ex-1lnx+(2x-1)ex-1+1-2x2,x∈(0,+∞),
则g′(x)=2xex-1lnx+x2ex-1lnx+(3x+1)ex-1-4x

易知h(1)=0,即g′(1)=0.

故g(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
故g(x)≥g(1)=0.
则f″(x-1)≥0在(0,+∞)上恒成立.
故f″(x)≥0在(-1,+∞)上恒成立.
即f′(x)在(-1,+∞)上单调递增.
易知f′(0)=0,故当x∈(-1,0)时,f′(x)<0,当x∈(0,+∞)时,f′(x)>0,故f(x)在(-1,0)上单调递减,在(0,+∞)上单调递增,则f(x)≥f(0)=0.
故当x>-1时,(ex-1)ln(x+1)≥x2.
点评整体构造函数后,将所证问题转化为求解函数的最值是处理此类证明问题的基本思路.本题运用此法解题时,其难点在于所证不等式中的指对数以“抱团”的乘法形式出现,因此在求解的过程中对数学计算以及逻辑推理的核心素养做出了更高层次的要求.
思路2分而治之,逐个击破.
解法2显然x=0时,(ex-1)ln(x+1)=x2=0,即(ex-1)ln(x+1)≥x2成立.


故当x>0时,h′(x)>0,当-1 则h(x)>h(0)=0. 即g′(x)>0,所以g(x)在(0,+∞)上单调递增,则g(x)>g(0)=0. 则f′(x)>0. 故函数f(x)在(-1,0)和(0,+∞)上单调递增. 由洛必达法则可知, 故f(0)=0. 当x∈(-1,0)时,f(x)<0,ln(x+1)<0,f(x)·ln(x+1)=(ex-1)ln(x+1)>0,同理可得当x∈(0,+∞)时,(ex-1)ln(x+1)>0. 故当x∈ (-1,0) ∪(0,+∞)时,(ex-1)ln(x+1)>0. 综上所述,当x>-1时,(ex-1)ln(x+1)≥x2. 解法3显然x=0时,(ex-1)ln(x+1)=x2=0. 即(ex-1)ln(x+1)≥x2成立. 令h(x)=(1-x)ex-1,则 h′(x)=-xex. 当x<0时,h′(x)>0,h(x)单调递增; 当x>0,h′(x)<0,h(x)单调递减. 所以h(x)≤h(0)=0,当且仅当x=0时等号成立. 所以g(x)在(-∞,0)和(0,+∞)上单调递减. 易知当-1 当x>0时,x>ln(x+1)>0, 所以g(x) 又当x>-1且x≠0时,x(ex-1)>0, 所以(ex-1)ln(x+1)>x2. 综上所述,当x>-1时,(ex-1)ln(x+1)≥x2. 点评分离参数或分离函数的目的是使得复杂的函数问题简单化,因此在分离时,应当联想常用的函数模型,选择合理的分离,使得分离后得到的新函数的性质可以信手拈来.本题在分离的过程中有两种选择,一是单纯地处理ln(x+1),如解法2;二是将ex-1与ln(x+1)同时变形,如解法3. 思路3对数平均,化繁为简. 解法4显然x=0时,(ex-1)ln(x+1)=x2=0,即(ex-1)ln(x+1)≥x2成立. 当x≠0时,由对数均值不等式可得 易知xln(x+1)>0. 故(ex-1)ln(x+1)>x2. 综上所述,当x>-1时,(ex-1)ln(x+1)≥x2. 思路4积分领航,几何杨帆. 解析5 显然x=0时,(ex-1)ln(x+1)=x2=0,即(ex-1)ln(x+1)≥x2成立. 图的大小比较 图的大小比较 则(ex-1)ln(x+1)>x2. 则(ex-1)ln(x+1)>x2. 综上所述,当x>-1时,(ex-1)ln(x+1)≥x2. 点评定积分的几何意义是曲边梯形的面积.若遇到分式结构,可以考虑通过变形转化为某个函数在区间上的定积分,进而联系几何意义,实现数形结合,进而快速解决问题. 思路5中值定理,如履薄冰. 解法6显然x=0时,(ex-1)ln(x+1)=x2=0,即(ex-1)ln(x+1)≥x2成立. 当x≠0时,由于xln(x+1)>0,则 (*) (ex-1)ln(x+1)≥x2. 综上所述,当x>-1时,(ex-1)ln(x+1)≥x2. 思路6泰勒展开,否极泰来. 解法7由泰勒公式可知, 此时ln(x+1) ≥0, 此时ln(x+1)≤0, 故要证(ex-1)ln(x+1)≥x2, 令f(x)=(2+x)ln(x+1)-2x, 当x≠0时,由对数平均不等式,得 综上所述,当x>-1时,(ex-1)ln(x+1)≥x2. 故当-1 当x>0时,f″(x)>0, 故f′(x)在(-1,0)上单调递减,在(1,+∞)上单调递增. 则[f′(x)]min=f′(0)=0. 故f′(x)≥0. 即f(x)在(-1,+∞)上单调递增. 综上所述,当x>-1时,(ex-1)ln(x+1)≥x2. 图3 切线放缩 图4 凹凸反转 通过观察题目,不难发现y=ex-1与y=ln(x+1)互为反函数,两者的图象关于直线y=x对称,且该直线为公切线,两个函数在公共的定义域内都存在着明显的凹凸性,于是笔者认为本题的命题思路如下: 第一步,选取一个凹(凸)函数f(x),明确函数的单调性; 第二步,在(x0f(x0))处作曲线y=f(x)切线y=h(x),保证f(x)≥h(x)或f(x)≤h(x)恒成立,且等号仅在x=x0处取得; 第三步,求解曲线y=f(x)关于直线y=h(x)的对称曲线y=g(x); 第四步,构造不等式f(x)·g(x)≥[h(x)]2,其中等号只在x=x0处取得. 在近年的高考中,以泰勒展开式为背景的不等式问题屡见不鲜,因此笔者认为,在教学时,有必要增加对部分高等数学知识的渗透,既提高了解题效率,又避免了复杂的运算,使得学生能够会当凌绝顶,一览众山小[3].








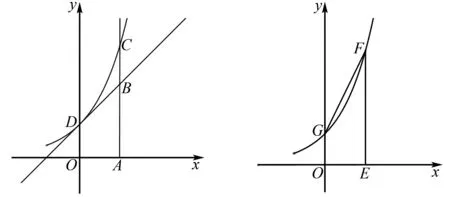



















3 命题思路
