铜铝导体超声波焊接温度场模拟研究

尚小良

（比亚迪汽车工业有限公司， 广东 深圳 518118）

1 金属超声波焊接原理及应用

超声波焊接是母材不发生熔化的一种固态焊接技术，能实现同种或异种金属的组合焊接连接[1]。其基本原理是焊接设备发生器通过换能器将高频电能向高频机械能进行转换，焊头将高频的机械能通过往复摩擦的形式作用在焊接金属母材上，在摩擦热和静压力共同作用下使被焊金属母材之间产生晶格结构重组从而实现结合的一种技术。金属在进行超声波焊接时，既不向工件施以高温热源，也无需向工件添加助焊辅料，只是在超声振动频率和静压力的共同作用下将能量转变为工件间的摩擦功、形变能及有限的温升使接头达到冶金级别结合[2]。因此金属超声波焊接具有安全、环保、焊接效率高的优势，可广泛应用于汽车线束电缆、锂电池极片、极耳以及铜铝导电母排的焊接。

2 金属超声波焊接成型机理

超声波焊接技术自上世纪发明后虽已广泛应用于各行业，但对超声波金属焊接接头的形成机理仍然存在诸多争议，尚未形成统一的认知。超声波金属焊接过程复杂，且涉及金属间的机械嵌合，也存在金属原子间的扩散和晶粒的再结晶过程[3]。以下概括总结了金属超声波焊接过程的4个阶段，很好解释了内在成型机理的演变规律。

1） 机械嵌合。在超声波焊接初期由于焊接时间短，焊接压力较小，焊接界面摩擦热能和金属形变能不足，而未能穿透焊接母材镀层（镀银） 作用到紫铜基材。此时的焊接界面只是在外力作用下，大部分与母材表面镀层相互挤压，摩擦形成的机械嵌合。机械嵌合通常呈现涡流或锯齿状[4]，这种嵌合仅是宏观上机械互锁，在外力作用下容易脱落，因此焊接母材的机械嵌合连接并不是超声波焊接主要结合机制。

2） 原子扩散。随着焊接压力和时间的增加，由于焊接界面的摩擦热引起的温度升高，金属原子热运动加剧，当其获得的能量大于其扩散激活能时，原子发生扩散。金属的扩散机制[3，5]是由于体系内原子在有化学式或电化学梯度情况下，所发生的定向流动和相互混合过程，即内部结构的缺陷是由于焊接界面在摩擦热和金属形变能综合作用下母材发生剧烈塑性流动，造成材料晶体间隙、空位、错位、破碎等晶体缺陷密度急剧增大[5]；其次是机械嵌合阶段时，使得界面两侧金属的接触面积显著增加，有利于焊接界面处原子之间的相互扩散。

3） 金属键合。铜铝焊接母材在摩擦热能和形变能的共同作用下，当金属原子获得的能量大于其扩散激活能时，原子发生扩散，随着金属原子扩散距离进一步减小，当金属材料界面间原子之间距离达到纳米级别时金属原子即形成键合，金属之间的键合作用大幅增强了焊接的结合强度。当焊接工艺参数合适时，焊接接头的部分力学性能超过了母材[6]，导电性能也十分优异。因此在铜、铝导电母材超声波焊接成型过程中，金属键合起关键作用。

4） 金属再结晶。原子的扩散是指获得的能量大于其扩散激活能时，原子发生扩散，此时由温度和压力引起的母材晶体缺陷具有自发从热力学不稳定的高自由能状态恢复到未变形时低自由能状的趋势，即随着焊接温度的升高，金属将发生回复、再结晶和晶粒长大的过程。其中，回复是指在加热温度低于变形紫铜发生再结晶温度时，由于原子的激活能不大，只能做短距离的扩散运动，此时只是消除晶格的畸变缺陷，但不能形成新的再结晶晶粒。当变形金属的加热温度进一步高于回复温度时，在变形组织的基体上产生新的无畸变的晶核，并迅速长大形成等轴晶粒，逐渐取代全部变形组织的这个过程称为再结晶[7]。

3 金属超声波焊接再结晶温度

金属材料的再结晶行为是在一定温度的范围内产生的，而材料能进行再结晶的最低温度称为该材料的再结晶温度。变形金属的再结晶与液体结晶及同素异构体转变不同，它没有一个固定的结晶温度，而是受多种因素的影响，其中影响最大的是金属的变形程度，随着变形程度的增大，材料内部的储能越大，再结晶的驱动力也越大，作用的再结晶温度就会降低[8]。另外金属的原始晶粒尺寸越小，再结晶温度越低，通常变形程度较大的纯金属或合金，材料的再结晶温度约为0.3～0.4Tm。根据金属的变形程度不同，在30%～80%熔点温度都可以发生再结晶行为，因此未达到母材熔点的焊接称为固态焊接。紫铜的熔点为1083℃，因此紫铜温度约为380～430℃时即可发生再结晶。6系铝合金熔点660℃，经过较大冷变形的铝合金的再结晶温度约350～420℃。

金属超声波焊接时不向工件施加高温热源，焊接时有限的温升显然并未达到母材的熔点，故金属超声波焊接过程中的焊接温度一直是学者的研究对象。

4 铜铝超声波焊接温度场仿真模拟

由于超声波焊接作用时间短，焊接界面是封闭面，外在的观测和测量手段无法精确地测量焊接界面的温度场变化。通过前人的一些研究，对超声波焊接再结晶成型的过程有了很好的了解，但对该过程的温度场变化缺少认知。

以下采用ABAQUS有限元分析软件对铜铝材的超声波焊接温度进行仿真模拟，以检验焊接界面区域的温度是否达到母材的再结晶温度。

4.1 实验材料及设备

4.1.1 实验材料

本模型的焊接材料研究对象为长45mm×宽23.5mm×厚3.5mm表面镀银紫铜板，直径16mm的6101铝合金圆棒材，前端被冷压成长22mm×宽22mm×厚7.5mm矩形鼻子，将紫铜板焊接在铝合金矩形鼻子上。

4.1.2 焊接方式

本实验模型采用卧式超声波焊接机进行焊接。由于铝材较厚，焊接能量穿透困难。此外铜材熔点高，焊头作用在铜板材上引起铜材发生更大程度的变形，可以降低其发生再结晶的温度。所以采用“铜上铝下”的方式进行超声波焊接实验，超声波焊接-零部件结构示意和剖面图如图1、图2所示。

图1 超声波焊接-零部件结构示意图

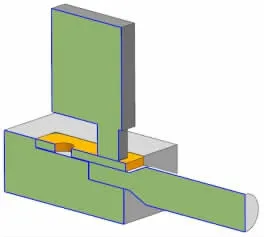
图2 超声波焊接-零部件结构局部剖视图

4.1.3 实验设备参数

本实验使用某国外品牌超声波焊接机，最大输出功率8kW，焊接示意见图3，焊接时采用能量模式，设备振动频率、振幅、焊头面积保持不变，焊接压力和总焊接能量为控制变量。具体超声波焊接参数见表1。焊接设备及焊接效果如图3所示，在使用表1焊接参数后，实测焊接点平均拉脱强度超过8000N，故结合强度可靠。

表1 超声波焊接参数

图3 焊接设备及焊接效果

通过对焊接结合点横切面进行电镜晶相分析，可见铜铝形成了约20～25μm的扩散带，如图4所示，铜铝组织的扩散和实际拉脱强度能证明铜铝焊接面发生了再结晶结合。

图4 铜铝焊接面处晶相图

4.2 铜铝材有限元模型的建立

4.2.1 有限元模拟问题简化与假设

本次研究采用ABAQUS有限元分析软件进行，鉴于超声波焊接实际工况过程的复杂性，在研究之前，需要对实际的模型进行简单优化，对于一些影响不大的因素进行了假设：①假设焊头、焊接件、基座等之间接触为理想无间隙接触；②焊接过程中，焊头和底毡对铜铝工件的驱动力远大于工件焊接面摩擦力，相对运动激发的热流只发生在焊接界面；③环境温度在整个研究过程恒定为t0=20℃；④焊头面积等于母材塑性形变面积。

4.2.2 材料参数

通过查阅相关书籍以及文献，得到焊头以及基座的物理性能参数如表2所示，紫铜和铝合金的物理性能参数见表3、表4，在确认以上数据后，采用20℃的属性建立有限元分析模型。

表2 焊头及基座材料物理性能参数

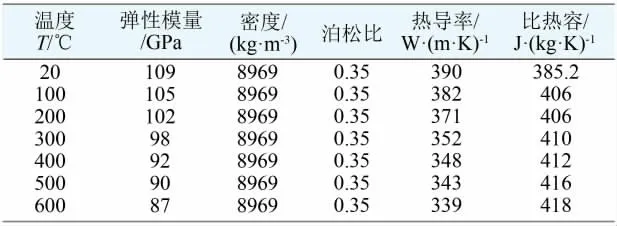
表3 紫铜的物理性能参数

表4 铝合金的物理性能参数

4.3 对有限元模型进行网格划分设置

网格划分就是为了将模型分成很多小的具备计算能力的单元，是有限元分析前处理设置中的重中之重，不合理的网格划分会导致求解中断而无法继续分析。鉴于实物模型类似于板类结构，采用六面体网格进行划分，还能降低计算机的计算时间。本次仿真使用的单元类型为8节点线性传热六面体单元DC3D8。有限元网格模型如图5所示。

图5 有限元网格模型

4.4 载荷的设置

本次研究端子焊接过程的温度场分布涉及到热量的产生和传导。其中，热量的传导主要分为热传导、热对流以及热辐射；热量的产生主要由端子之间的塑性变形热以及摩擦生热所得[9]。下面先来计算热量的产生，其次再来计算这个过程中的散热问题。

4.4.1 塑性变形热的热流密度计算

超声波焊接中塑性变形热流密度为：

式中：FW——焊接力的计算。公式为[9]：

式中：FW——焊接力；Y（T）——取决于温度的屈服强度值；ADZ——塑性变形区面积；FN——焊接静压力；AW（t）——焊接面积。

在焊接过程中，前期截面只是小部分区域的机械结合，结合面积远小于焊头面积，随着焊接的持续，材料在压力和升温后会发生塑性流动，焊接面积大大提高，因此可以得到一个近似公式：

K为常数，本文借鉴吴宗辉等人的关于钛合金焊接时间和焊接面积的实验拟合数据，取值39[3]。综上，FW见式（4）：

此外，超声波焊接的平均速度Vavg计算步骤如下所述。超声振动遵循正弦规律，其中位移S可表示为：

对式（5）求导得到：

对式（6）积分得到：

而ω=2πfw，则：Vavg=4ε0fw。

式中：ω——正玄角速度；ε0——振幅。

综上所述，最终塑性变形热流密度理论计算式如下：

由于材质屈服强度和温度呈负相关，在20℃温度下紫铜屈服强度为70～90MPa，AL合金屈服强度为65～80MPa，取铜铝屈服强度的最大数值后结合现场实际工艺参数，将数值各代入上述，可得QW≈9.8×10-6W/mm2。

本次实验采用的超声波焊接设备最终作用在焊头上的做功频率约为发生频率的90%，则fw取18kHz。

4.4.2 摩擦热的热流密度计算

式中：QFR——摩擦热流密度；FFR——焊接摩擦力；AFR——摩擦面积。因为FFR=uFN，将Vavg=4ε0fw代入式（9），可得：

此外，焊接压力约为0.2275MPa，该数值是代表设备中气缸的压强，而加载在试样上的垂直压力则需要经过下式进行计算。

式中：FN——静压力；Pq——气缸的压强；Dq——气缸的直径。设备的气缸直径为200mm。将气压的压强0.2275MPa以及气缸的直径200mm代入公式（11），可求得FN≈7147N。

查阅资料，取铝铜件表面的摩擦系数u=0.22，则理论计算的摩擦热流密度为QFR≈30.8W/mm2。

4.4.3 热对流散热量的确定

超声波焊接是属于非稳态导热的模型，焊接时间短，本文分析采用半无限大的非稳态导热模型，鉴于有稳定的热流密度输入的情况，符合采用第二边界的要求，可采用公式（12）进行求解。

将相应的参数填入公式（12），可以算得：当x=0时，1.65s后的温度为t（0，1.65）=630.6℃；当x=0.0035m时，1.65s后的温度t（0.0035，1.65）=502.4℃。

鉴于实际情况，焊接处的热流密度不单单向x方向（垂直焊接界面） 传递，其还会向着y和z的方向传热，热量传动方向示意图如图6所示。先假设热量正向传递的有效率为85%，将上述温度进行修正，则：当x=0时，1.65s后的温度为t（0，1.65）=536℃；当x=0.0035m时，1.65s后的温度t（0.0035，1.65）=427℃。

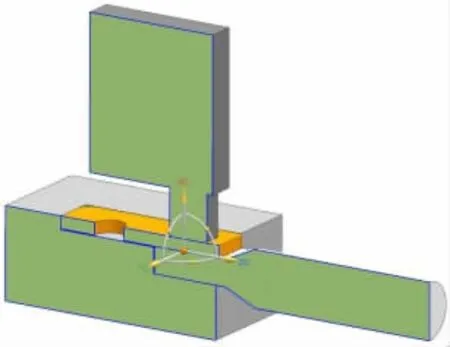
图6 热量传动方向示意图

在本研究中，热对流模型采用的是大空间内自然对流传热，在工程计算中，常用以下形式的大空间自然对流实验关联式：

但对于平板和圆柱这两种比较典型的模型，根据前人的大量数据可以简化取值。但是需要计算出Gr值才能进行数值的确定。而Gr数可根据Gr

式中：αv——体胀系数，αv=1/T；υ——运动粘度；Δt——表面温度差；l——特征长度；qh——散热热流密度；g——重力加速度；λ——导热系数。

Pr数值可根据定性温度tm查得，一般介质为空气时，该数为0.6～0.7。针对热面向下（冷面向上） 的情形，努塞尔数可采用以下公式：

将Gr代入式（13）可得：

由上述公式，可完成热对流散热量的计算。

在本次的模拟中，已知大气环境温度假设为20℃，铜排的表面温度为427℃，求得定性温度tm约为220℃，通过查阅资料插值取相应的空气物性参数如下：运动粘度υ为37.154×10-6m2/s；导热系数λ为0.04066W/（m×k）；Pr普朗特数为0.695。求得对流换热系数如下。

则相应的热对流散热热流密度为：

4.4.4 热辐射散热量计算

根据斯忒藩-玻尔兹曼定律，一个物体的空间辐射换热量热流密度可以按下述公式进行计算：

式中：ε1——发射率；σ——玻尔兹曼常数。

已知环境温度为20℃，代入铜排的最高温度536+273K，计算得出：qθ=0.01456W/mm2。

4.4.5 计算小结

从上面的计算中，可以得出热量主要由摩擦产生。在实际情况下，设备作用的功产生的热量存在部分是通过热传导、热对流以及热辐射对周边进行散热传递了出去，具体数值和占比见表5。可见散失的热量与产生热量相比较占比较小，可以看成绝热状态进行后续的分析。在本研究中，热传导占据了主导的地位。

表5 各热流密度与摩擦生热热流密度占比

4.5 模拟结果及分析

将计算的理论摩擦热流密度载入到有限元模型中，截取焊接时间为210ms、850ms、1650ms时的模拟结果如图7～图9所示，铜排及设备的参数见表6。

表6 铜排结构参数及设备焊接参数

图7 时间为210ms时的温度场结果

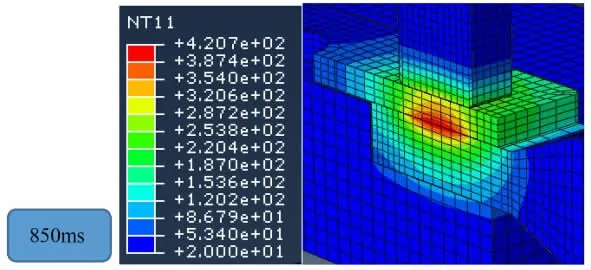
图8 时间为850ms时的温度场结果

图9 时间为1650ms时的温度场结果

焊接中心点的温度依次为：420.7℃、527.8℃，铝的熔点是660℃，其最高温度分别为铝熔点的63.7%、79.9%，铜的熔点是1083℃，其最高温度分别为铜的熔点的38.8%、48.7%，在大家认同的30%～80%范围之内，此外，模拟结果中心的最高温度和前期假设的85%有效转化率的中心最高温度结果536℃对比，误差约2%，再观察该条件下的铜排的表面温度为421℃，误差不到1%，说明本次的模拟结果以及假设的热流流失百分比是比较合理的。

选取焊接结合面中心的单元格绘制温度随时间变化曲线图如图10所示，可以得到以下结果。

1） 六面体的8个节点，焊接界面同一侧的4节点温度相差基本相同，不同一侧的单元结果也相差不大。这一相差的结果随着网格的细化，也会逐步减小。

2） 焊接在前200ms内，温度由环境温度20℃骤然升到约260℃，由此可以了解到，在超声波焊接过程中，能量的转化是非常快的，后续的温度随着时间呈缓慢线性上升，最终在850ms时，中心处的最高温度到达420.7℃。符合变形铝的再结晶开始温度350～420℃，铜的再结晶温度为380～430℃。随着时间增加，摩擦界面温度继续上升，来到1650ms时，到达铝的熔点温度的80%，故可以推论出：在焊接的前850ms内，母材的快速变形和摩擦热加速了母材原子的相互扩散；在到达850ms～1650ms过程中，焊接面的温度达到变形铜铝的再结晶温度，铜铝母材在焊接界面的变形组织基体上产生新的无畸变的晶核，并迅速长大形成等轴晶粒，逐渐取代全部变形组织，完成再结晶结合。

3） 摩擦界面中心温度最高，并且迅速通过内部向母材四周热传导，越远离中心面区域的温度越低。故焊接产生的热量，大部分通过热传导被母材热容吸收，留在铜排铝杆之间产生了温度场的变化。

5 结论

通过ABAQUS有限元模拟，能较准确地还原金属超声波焊接过程中的温度场变化，其仿真模拟的结果与理论的再结晶成型过程所需的温度高度吻合。利用有限元模拟的方法了解金属超声波焊接温度场的变化规律，能在设计初期掌握焊接模型的结构变化对焊接品质产生的影响，为设备的焊接提供参数预设指导，能有效提高开发和测试效率。