基于等价输入干扰估计的电子分析天平前馈控制
2023-10-25赵冠华杨传国吴静
赵冠华,杨传国,吴静
(商洛市计量测试所,陕西商洛 726000)
电子分析天平是一种具有高性能的精密计量仪器,广泛用于医药、国防、实验室、质量控制等领域。电子分析天平的质量传感器结构复杂,响应较慢[1-2]。一般采用电磁力反馈平衡零位法原理,因此天平系统平衡调节的稳定与快速是实现仪器准确、快速称量的重要因素[3]。
传统电子分析天平一般采用PID(比例积分微分)控制来实现,调节相关参数可以在一定范围内达到稳定可靠的要求[4]。传统PID整定参数固定,不能及时在线调整,存在自适应性差、调节时间长等缺点[5]。
基于闭环传递函数,Tomizuka提出了零相差跟踪控制器的控制策略[6],采用零极点相消的方式消除了系统的相位误差,可以达到快速称量的目的,文献[7]将此方法应用在电子天平中,但依然存在增益误差,且这种控制方式需要知道超前值,而超前值很难获取。文献[8]采用时间最优控制与模糊PID 控制相结合的控制策略进行实时控制,既可发挥时间最优控制快速消除大偏差的优点,又能发挥PID 控制精度高、超调小的优点,达到准确、快速测量的目的,但是在切换两者控制方法时控制器可能出现畸变现象,从而导致切换点处不稳定的情况。周围环境变化及建模不准确均会不同程度地影响电子分析天平的称量准确性,文献[9]通过分析影响电子天平称量准确度的原因,将外部环境温度和湿度数据作为模型输入,运用BP 神经网络寻找最优参数,建立电子天平称量误差模型并进行误差补偿,但是这种算法本质上为梯度下降法,而它所要优化的目标函数非常复杂,因此会出现“锯齿形现象”,并且受数据样本的局限。为了得到简单而快速的控制方法,提出一种基于等价输入干扰(EID)的前馈控制策略,提高了称量的快速性与稳定性,缩短了系统的稳定调节时间,并且控制方式具有较强的适应模型能力,示值误差优于国家标准JJG 1036—2022 《电子天平检定规程》规定的I级天平指标。
1 电子分析天平的数学模型
电子分析天平是实验室最常用的称量仪器,一般由电磁力平衡传感器、调节电路等许多设备组成。在不考虑其它干扰的情况下,电子分析天平名义模型的传递函数Gn[10]可表示为式(1)或式(2):
式中:K——传递比例系数;
T0——时间常数;
s——拉普拉斯算子;
ξ——衰减系数。
对电磁力平衡传感器的开环系统进行系统辨识,可以得到相应的系统参数,则电磁力平衡传感器系统的近似传递函数G1[10]按式(3)计算 :
2 控制器的设计
在带有干扰观测器的电子分析天平上,加入数字前馈控制器及带有EID估计器的电子分析天平的闭环反馈环节。控制器结构如图1所示。

图1 控制器结构图
2.1 EID估计器的设计
考虑如图2(a)的线性时不变系统按式(4)表示:

图2 EID原理图
式中:A、B、C、B——系数矩阵,A∊Rn×n,B∊Rn×nu,C∊Rny×n、Bd∊Rn×nd;
x0(t)——状态变量,x0(t)∊Rn;
u(t)——控制输入,u(t)∊Rnu;
y0(t)——控制输出,y0(t)∊Rny;
d(t)——外部扰动,d(t)∊Rnd。
假设被控对象是能控和能观的,且在虚轴上没有零点。
当矩阵B和Bd的维数不同时,扰动便会通过不同的渠道加在被控对象上,扰动等价到输入端后的对象如图2(b)所示,等价后的系统按式(5)表示:
令控制输入u(t)为零,如果对于所有的t≥0,系统(5)输出都满足y1(t)≡y0(t),那么,扰动de(t)就叫做扰动d(t)的EID[11]。
基于EID的控制结构[12]如图3所示。


图3 EID控制结构图
对系统的状态空间描述设计状态观测器,按式(6)计算:

如果存在Δd(t)满足式(8):
把式(9)代入式(8),并令EID的估计值得:
则可得式(10):
由式(6)和式(10)可得:


2.2 前馈控制策略
数字前馈和带有EID估计器的电子分析天平的闭环反馈构成的复合控制方法简单而有效地提高了信号跟踪的精度,且易实现,复合控制策略结构如图4所示[13-14]。

图4 复合控制结构图
由于该复合控制方法具有对信号畸变不敏感的特性,所以可以避免测量畸变的瞬态影响,保证系统的稳态性能。
3 仿真实验结果分析
根据电子分析天平的结构和实验参数,利用MATLAB软件建立电子分析天平模型,进行仿真分析,以检验基于EID的前馈控制方法调节的有效性。
3.1 加卸载仿真
分别对使用传统PID控制和基于EID前馈控制的电子分析天平系统进行仿真,在第1 s时加载质量为100 g,并于1.5 s后卸载,得到的质量仿真曲线如图5所示。

图5 加卸载仿真曲线
由图5 可见,虚线为PID 控制,实线为基于EID前馈控制。实线稳定在100 g值附近比虚线要早很多,这说明基于EID前馈控制调节时间短;实线率先到达预设值100 g,这说明基于EID 前馈控制响应快;虚线超出预设值100 g很高,而实线超出预设值100 g很低几乎无超调,这说明基于EID前馈控制超调小,因此与传统PID控制相比,基于EID前馈控制的电子分析天平系统具有调节时间短、超调小、响应快的优势。通过对图5 中相关数据进行统计分析,当输出质量与加载质量之间误差为0.1 mg时,传统PID控制的调节时间为1.30 s,基于EID前馈控制的调节时间为0.57 s,可以看出基于EID前馈控制能够快速达到输出稳定。
在实际称量及天平检定时,有时会进行多次加载,对这种情况进行仿真,在第1 s时加载100 g的基础上,于1.5 s 后再加载10 g,得到的质量仿真曲线如图6所示。

图6 连续加载仿真曲线
由图6 中数据可以看出,连续加载采用基于EID前馈控制的称量系统在0.57 s后达到输出稳定,且不超调,称量结果为110.000 3 g。优于国家标准JJG 1036—2022 《电子天平检定规程》规定的I 级天平示值误差指标[15]。
3.2 变系统参数仿真
受制造厂家永磁体、簧片等传感零件的工艺制造以及材料的制约,电磁力平衡传感器输出一致性参差不齐,再加上实际测量中存在误差,因此所构建的电磁力平衡传感器的数学模型会存在一定的误差。虽然采用EID估计器对传感器的数学模型进行补偿,但仍存在误差。为了更大程度减少模型误差的影响,通过改变数学模型中的参数来检验控制方法对不同传感器的适应性。传递函数为Gn=,分别改变a、b、c的值,对相同输入下(加载10 g)电子分析天平质量仿真曲线进行比较。其仿真结果如图7所示。
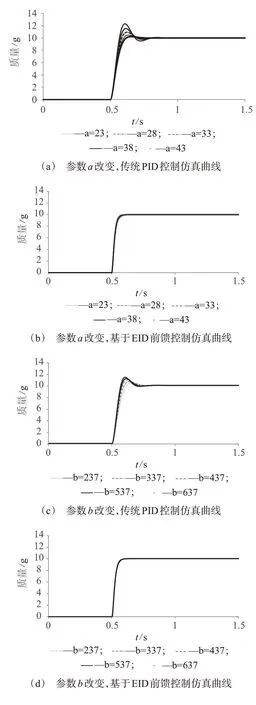

图7 系统模型参数变化时质量仿真曲线
参数的扰动对控制的影响就是看仿真曲线的一致性,如果一致性较好,则说明参数的扰动对控制的影响小,反之则影响大。从图7 中(a)与(b)、(c)与(d)、(e)与(f)中可以看出,所有的参数a、b、c中,传统PID 控制仿真曲线在参数变化时曲线变化较大,一致性较差,而基于EID 前馈控制仿真曲线在参数变化时曲线变化很小,一致性较好,因此对于相同的输入信号,当传感器系统的参数发生变化时,采用基于EID前馈控制方法的一致性明显要优于传统PID控制方法,体现了其对传感器系统数学模型依赖性小的优势。
4 结语
研究了一种带有EID估计器的前馈控制方法并将其应用于电子分析天平的控制中。其中,EID 估计器对未建模部分及参数摄动等干扰进行估计并补偿,数字前馈和带有EID 估计器的电子分析天平的闭环反馈构成的复合控制方法达到了快速、准确测量的目的,为计量专业人员以及科研人员提供了比较准确的称量值。仿真实验结果表明了该方法提高了称量的稳定性与快速性,缩短了系统的稳定调节时间,且具有较强的适应模型能力,调节效果明显高于传统PID控制方法。
