考虑双目竞争视觉现象的非对称失真立体图像质量评价方法
2023-10-24唐祎玲江顺亮徐少平肖建陈晓军
唐祎玲,江顺亮,徐少平,肖建,陈晓军
南昌大学数学与计算机学院,南昌 330031
0 引言
随着立体图像获取、传输、处理及显示技术的发展,立体图像质量评价(stereoscopic image quality assessment,SIQA)研究变得越发重要(方玉明 等,2021)。获取能够准确描述双目输入特性的特征,并依据这些特征估计立体图像实际感知质量是SIQA的核心设计目标之一(Shen 等,2021;Liu 等,2020;Li等,2019)。根据立体图像左右视点图像失真的对称程度,可以将立体图像分为对称失真立体图像和非对称失真立体图像。对称失真立体图像的左右视点图像失真类型相同,且失真程度也较为接近。已有的SIQA 算法在评价对称失真立体图像时,取得了较高的评价准确性。然而,在实际应用中立体图像更容易出现非对称失真的情况,即左右视点图像具有不同的失真程度或失真类型,许多SIQA 方法难以准确地评估此类图像的质量。如何准确描述左右视点图像的非对称失真特性,并利用这些信息提升SIQA方法评价非对称失真立体图像的准确性和鲁棒性具有重要的研究意义(Fang等,2021;Shao等,2018)。
较早的SIQA 算法通常使用已有的二维图像质量评价(image quality assessment,IQA)方法预测立体图像质量。例如,Benoit等人(2009)、Yasakethu等人(2008)使用多种全参考IQA 算法估计单目图像的质量值,将两个视点图像的质量均值作为最终的立体图像质量预测值。然而,人类视觉系统(human visual system,HVS)中的立体视觉感知是通过大脑的初级视觉皮质对双目输入信息进行复杂处理后产生的,简单地将左右视点图像质量值进行平均,无法模拟人类视觉这种复杂的生理机制,因此早期SIQA方法在评价非对称失真立体图像的质量时,预测准确性会明显下降。
双目竞争与融合是人类立体视觉生理中的现象,当两眼输入的信息较为一致时,双眼的信息能够较为容易地实现融合,当两眼输入的信息存在如几何结构差异、失真等不一致时,会出现双目竞争现象(Han 等,2017)。基于双目融合与双目竞争的研究为立体图像质量评价模型的构建提供了新的依据(Su 等,2015b)。许多立体图像质量评价研究发现,当两眼输入不同时,某一眼输入在视觉信息识别过程中产生主导作用(Chen等,2013a;Wang等,2017),使得在立体图像质量判别中,某一视点图像的视觉质量相比于另一视点图像的视觉质量对整体质量评价产生更大的影响(Shao等,2015)。同时,视觉感知的最终目标是从视觉场景中有效地提取有用信息,包含有用信息更多的视点图像应具有更大的权重(Wang和Li,2011;Liu等,2017)。
一些学者在双目竞争现象的启发下建立了基于左右视点图像融合的立体图像质量评价模型,用于提升非对称失真立体图像的质量评价准确性。Chen 等人(2013a,b)利用Gabor 滤波响应模拟双目输入的刺激强度,融合一幅用于体现双目竞争的独眼图像,分别构造了基于独眼图像的全参考(cyclopean image-based full-reference,CIFR)SIQA 算 法(Chen 等,2013b)和基于独眼图像的无参考(cyclopean image-based no-reference,CINR)算 法(Chen等,2013a)。Su 等人(2015a)在CINR 算法的基础上,结合左右视点图像之间的视差图合成收敛的独眼图像(convergent cyclopean),并提取融合图像中的空域和小波域中的双目特征用于图像质量评价。Liu 等人(2017)认为立体图像质量的感知往往由包含更多空间活动的图像主导,提出了基于独眼图像、双目乘积图的立体综合质量(S3D integrated quality,SINQ)算法。Yue 等人(2018)使用协方差矩阵来获取独眼图像中的结构信息,以及左右视点图像的梯度差异图来估计非对称失真立体图像的质量值。
由于融合独眼图像较为耗时,一些学者将左右视点图像的质量值加权平均来预测立体图像质量值。Wang 等人(2014)提出基于信息内容和失真权重的结构相似性(information content and distortion weighted structural similarity,IDWSSIM)比较算法以计算两个视点图像的质量值权重。Shao 等人(2015)结合左右视点图像特征的稀疏性和双目竞争原理,估计左右视点图像的权重系数,实现两个视点图像质量值的融合。Ma 等人(2018)利用结构相似性(structural similarity,SSIM)算法计算左右视点图像的质量值,并基于双目对比度和双目能量的差异将左右视点图像的质量值融合为立体图像的质量值。
还有一些学者探讨了利用左右视点图像特征融合的方式实现立体图像质量预测的方法。Shao等人(2018)利用字典学习方法估计左右视点图像特征的权重系数,融合左右视点的特征值,用于特征质量映射。沈丽丽和王莹(2020)提出了基于奇异值分解的融合方法,将左右视点图像以及左右视点图像的特征向量进行融合。
总的来说,上述方法采用了多种不同方式计算双目信息融合的权重系数,来模拟双目竞争现象。Chen 等人(2013a,b)认为双眼竞争时,某一个视点的Gabor 能量的增加会抑制另一个视点在图像质量感知中的作用,因此他们利用左右视图的规格化Gabor 滤波幅值响应来计算两幅图像的融合权重系数。Su 等人(2015a)使用可控金字塔的小波系数的计算左右视点的能量图,进而计算两个视点的权重系数。Liu 等人(2017)利用量化的单目图像的空间活动生成左右视点图像的融合权重系数。Wang 等人(2014)则通过计算空间位置的局部方差,构造左右视点的局部能量比图,计算左右视点的权重系数。可以看出,研究立体图像的左右视点信息融合的权重设置,模拟人类视觉中的双目竞争现象,能够提升非对称失真立体图像预测结果与人类主观评价的一致性。
由于在非对称失真立体图像质量的评价中,需要处理的失真情况十分复杂,如何将双目竞争应用于立体图像质量评价仍然是一个重要的研究内容,简化模型的构建方法对于将其运用到实际应用中非常重要。因此,本文提出了图像质量衰减系数,利用两个视点图像中包含的有效信息的不同,计算左右视点图像的图像质量衰减系数,量化单目图像质量改变的程度,判别左右视点对立体图像质量的影响程度,并依据双目竞争的视觉现象,利用图像质量衰减系数生成特征融合的加权因子,将单目图像在灰度空间与HSV(hue-saturation-value)彩色空间中的统计特征进行融合用于立体图像质量预测。此外,由于非对称失真立体图像左右视点图像之间的失真程度或失真类型不同,在结构以及所包含的信息量等方面也存在较明显的差异,本文构造左右视点图像的结构相似性映射图(binocular structural similarity,BSSIM),用于量化非对称失真立体图像左右视点的结构差异等双目差异特性。最后,将双目融合特征与双目差异特征串接在一起,建立基于支持向量回归(support vector regression,SVR)的特征—感知质量预测模型。
1 评价模型的总体框架
基于双目竞争的无参考非对称失真立体图像质量评价模型如图1 所示。考虑到非对称失真图像左右视点的质量衰减程度不同,计算图像质量衰减系数,用于融合从左右视点图像中提取的灰度空间和HSV 彩色空间特征,获得能够反映双目竞争视觉特性的图像质量感知特征。同时,通过构建BSSIM 进一步描述非对称失真图像两个视点之间的结构差异等双目差异特征。最后,使用已知人类主观评价值的图像训练基于SVR 的特征—质量映射模型。

图1 利用双目竞争的非对称失真立体图像质量评价算法总体框架Fig.1 The framework of the proposed asymmetrically distorted stereoscopic image quality assessment method based on binocular rivalry
2 图像质量感知特征提取与评价模型
2.1 基于图像质量衰减系数的双目融合特征提取
2.1.1 图像质量衰减系数
信息熵可以用来度量图像中包含的不确定性信息,与图像的质量以及图像的失真类型密切相关(Liu 等,2014;Sheikh 等,2005)。给定一幅图像,其灰度图像信息熵计算为
式中,pi表示图像中第i个灰度等级出现的概率。将左右视点图像的信息熵分别标记为El和Er。
图2 以立体图像基准测试数据库IVCIIWaterloo-IVC 3D IQA Database Phase II(Wang 等,2015)中的白噪声(white noise,WN)和模糊(gray blur,GB)对称失真立体图像为例,说明信息熵与立体图像失真类型及其质量之间的关系。两种失真类型均选取5 幅相同场景、不同失真程度的图像,信息熵按立体图像主观评价值(mean opinion score,MOS)取值从大到小的顺序排列。MOS 值越大,表示图像质量越高。

图2 失真立体图像信息熵及标准差随立体图像质量变化的取值变化图Fig.2 Variation of entropy and standard deviation of distorted stereoscopic image with MOS values((a)entropy of WN distorted image;(b)standard deviation of WN distorted image;(c)entropy of GB distorted image;(d)standard deviation of GB distorted image)
从图2(a)(b)可以看出,随着WN 失真图像中的噪声增多,图像质量下降、图像包含的信息量增大,数据的离散程度增大,相应地图像信息熵和标准差会随着图像质量的下降而增大,MOS 值接近的WN失真图像,其信息熵和标准差的取值也较为相近。从图2(c)(d)可以看出,对于GB 失真立体图像来说,随着图像的模糊程度逐渐增加,图像中的细节信息越来越少,图像信息熵和标准差的取值也会随着图像质量衰减程度的增加而降低。可以看出,不同失真类型立体图像的信息熵及标准差随图像质量变化的趋势并不相同,但对于同类失真图像,信息熵与标准差随图像质量变化的趋势一致且变化幅度不一样。
为了生成适用于多种失真类型图像的能够根据图像质量变化而线性变化的特征,本文将信息熵与标准差所表示的图像降质信息叠加,计算图像质量衰减系数,具体为
式中,σl和σr分别是左、右视点图像的标准差,El和Er分别是左、右视点图像的信息熵。C1和C2是用于保证公式计算稳定性的常数。
对同一场景、相同失真类型的立体图像,图像质量衰减系数dl和dr会随着图像质量值的改变而线性变化。图3展示了IVC-II数据库中WN和GB两类失真立体图像的dl和dr取值随图像MOS 值变化的趋势。

图3 图像质量衰减系数随MOS取值变化的变化图Fig.3 Variation of image quality degradation coefficients with MOS((a)WN symmetrically distorted image;(b)WN asymmetrically distorted image;(c)GB symmetrically distorted image;(d)GB asymmetrically distorted image)
图3(a)(c)给出了立体图像为非对称失真图像时dl和dr的取值随图像质量变化的情况,可以看出,当立体图像为对称失真图像时,由于对称失真立体图像的左右视点图像的失真类型相同、失真程度近似,其dl值和dr值基本相等,同时,两种失真类型图像dl和dr的取值都会随着图像质量的下降而减小。
图3(b)(d)给出了立体图像为非对称失真图像时dl和dr的取值随图像质量变化的情况。为了便于观察,图中所使用的是一个视点为原始图像、另一个视点为某类失真的非对称失真立体图像。从图3(b)(d)可以看出,当非对称失真立体图像的MOS 值减小时,无失真视点图像的图像质量衰减系数保持不变,而失真视点图像的图像质量衰减系数值减小。说明当两个视点中有一个视点失真时,失真视点的质量对立体图像的整体感知质量的影响更大,即当两个视点图像的失真程度不同时,出现了双目竞争,图像质量衰减系数取值小的视点会对立体图像的整体质量产生更大的影响。
2.1.2 单目图像特征提取
由于人类视觉系统对图像信息的感知是从局部到整体逐步形成的。本文在获取单目图像特征时,一方面从灰度空间获取图像局部分块的统计特征;另一方面从HSV 彩色空间提取图像整体的统计特征。
对一幅尺寸为M×N的灰度图像,首先采用均值减损对比度方法对其进行归一化处理,来获取具有显著统计特性的质量感知特征。灰度图像的归一化计算为
式中,I(i,j)是宽和高分别为M和N的图像;i和j是像素索引,i=1,2,…,M,j=1,2,…,N;μ(i,j)和σ(i,j)分别为I(i,j)的均值与标准差;C用于避免合成图像的方差为零;ωk,l是窗口尺寸为(2K+1) ×(2L+1)的二维高斯加权函数。
接着,将归一化图像划分为P个相同尺寸的图像块,使用图像分块的标准差、峰值和偏度作为部分质量感知特征。偏度S和峰度K计算为
式中,p是图像块的索引,p=1,2,…,P;W和H为图像块Ip(i,j)的 长和宽;i和j是各像素的索引,i=1,2,…,W,j=1,2,…,H;μp和σp分别为图像 块Ip(i,j)的均值与标准差。则左右视点图像的灰度空间统计特征向量可以表示为
颜色作为视觉质量感知的一个重要的参考因素,也应用于图像质量评价算法中。例如,Redi等人(2010)将颜色分布特征应用于部分参考图像质量评价中。Temel 等人(2016)基于YCbCr 颜色空间提取图像的结构信息,建立了基于无监督学习的图像质量评价模型。由于HSV 彩色空间包含的信息十分接近人类所能感知的颜色信息,本文从HSV 彩色空间中获取色度、亮度以及饱和度的统计信息作为图像质量感知特征的一部分。
对RGB 格式图像的红(R)、绿(G)和蓝(B)3 个分量进行变换,可以得到一幅图像各个像素的色调(H)、饱和度(S)和取值(V)分量,计算为
图像经过变换后,色调通道H的取值范围为0~360o,饱和度S和V的取值范围为0~1。将左右视点图像在HSV 颜色空间3个通道的均值、标准差、偏度以及峰度作为单目图像特征的一部分,则两个视点图像的HSV 彩色空间在3个通道上的统计特征向量分别记为
2.1.3 单目图像特征融合
由2.1.1 节的分析可知,本文所提取的图像质量衰减系数能有效地反映出单目图像质量的改变程度。当左右视点图像的失真类型和失真程度一致时,两个视点的图像质量衰减系数值近似相等;当左右视点图像为非对称失真图像时,图像质量相对差的视点,其图像质量衰减系数取值相对较小。因此,本文基于双目竞争的视觉现象,利用图像质量衰减系数生成左右视点图像质量感知特征融合的权重系数。并利用融合权重系数将左右视点图像的单目图像质量感知特征融合在一起,作为能够体现双目融合与双目竞争现象的立体图像质量感知特征之一。单目图像特征的融合权重系数wl和wr为
式中,dl和dr分别为左和右视点图像的图像质量衰减系数,wl与wr的和为1。
利用wl和wr对左、右视点图像的单目图像特征进行加权平均融合。两个视点的HSV 彩色空间的融合特征向量表示为
两个视点的灰度空间融合特征表示为
2.2 双目差异特征提取
2.1 节的分析表明,非对称失真立体图像左右视点之间的方差、信息熵和图像质量衰减系数存在较为明显的差异。因此,本文利用从左右视点图像之间的上述特征差来描述立体图像的非对称失真特性。将左右视点图像之间的方差差值Dv、信息熵差值DE以及图像质量衰减系数差值Dd作为左右视点图像之间的双目差异特征之一。3 个差值计算为
对于对称失真立体图像,其左右视点图像之间的失真类型相同,且两个视点图像之间的失真程度也较为接近,两幅失真图像的信息熵、方差、图像质量衰减系数的取值会较为接近,上述3 个双目差异特征的取值较小。而非对称失真立体图像左右视点图像之间的差异性较大,从两个视点图像中获得的特征的取值差异也会较为明显,双目差异特征的取值也会较大。
本文以非对称失真立体图像测试数据库IVC-I(Waterloo-IVC 3D IQA Database Phase I)(Wang 等,2014)和IVC-II中的图像为例,来说明双目差异特征所具有的区分对称失真图像与非对称失真图像的能力。图4 给出了两个数据库中所有图像的双目差异特征散点图。IVC-I数据库和IVC-II数据库包含3类非对称失真图像。1)一个视点图像为未失真图像,另一个视点图像为失真图像,记为RD(referencedistorted);2)左右视点图像的失真类型相同、失真程度不同的图像,记为DL(different distortion level);3)左右视点图像的失真类型不同的图像,记为DD(different distortion type)。
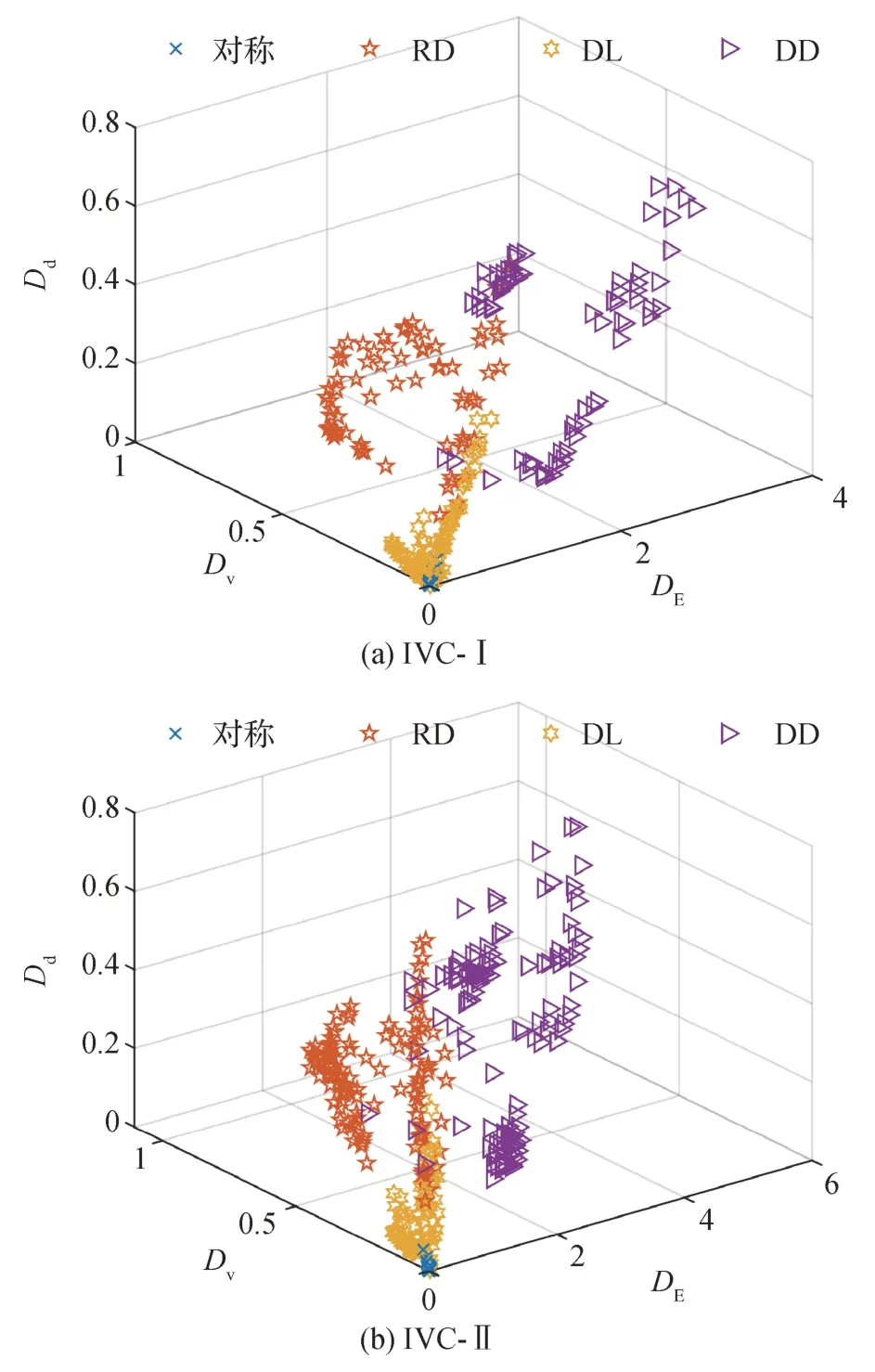
图4 左右视点图像的双目差异特征散点图Fig.4 Scatter plots of binocular difference features between the left and right views((a)IVC-I;(b)IVC-II)
从图4可以看出,对称失真图像与3类非对称失真图像的双目差异特征散点图分布在特征空间的不同区域。其中,对称失真图像的双目差异特征散点主要聚集于坐标系的原点处;由于DL类型的非对称失真图像只是左右视点图像的失真程度不同,3 个双目差异特征的取值变化较小,散点相对集中;RD类型的非对称失真图像,其左右视点图像的差异较DL 类型左右视点图像之间的差异更大,散点相对分散;DD 类型左右视点的失真类型不同,因此两个视点之间的差异最大,3 个双目差异特征的取值变化最大,散点最为分散。由上述分析可知,左右视点的3 个双目差异特征能够较好地描述非对称失真立体图像的失真特性。
除了上述3 种信息的差异,当立体图像为非对称失真图像时,左右视点图像在失真类型和失真程度上的差异较大,其结构上的差异也会增大。鉴于人类视觉系统对结构信息的变化十分敏感,本文进一步利用左右视点图像之间的结构相似性来反映两个视点之间的差异性特征。
经典的结构相似性比较SSIM 算法(Wang 等,2004)能够用来比较两幅图像之间的结构相似性。因此,本文利用该方法比较左右视点图像之间的结构相似性。如果立体图像的左右视点图像分别记为IL和IR,则左右视点图像的亮度l、对比度c与结构相似性s计算为
式中,μL和μR分别表示左和右视点图像的局部均值,σL和σR分别为左和右视点图像的局部标准差,σLR为左右视点图像的交叉相关标准差,C1、C2和C3是常量,用于减小饱和度在低亮度和对比度区域中的影响,同时用于避免当分母近似为零时的不稳定情况。则左右视点图像的BSSIM表示为
在计算左右视点图像的相似度时,使用滑动窗口对两幅图像的局部分块进行处理,用于减小图像统计特征的空间不稳定性,获取更多图像的结构变化信息。使用滑动窗口处理后的图像的局部统计特征计算为
式中,w 是一个尺寸为11 × 11 的高斯窗口,窗口标准差为1.5;x∈[IL,IR],N=11。
图5 以IVC-II 数据库中相同场景下的对称失真和非对称失真立体图像为例,用于说明BSSIM 对不同类型失真图像结构特性的描述能力。其中,图像从左至右依次为左视点、右视点和BSSIM。立体图像的BSSIM 清晰地展示了不同类型失真图像的左右视点图像结构上的不同。图5(a)所示为左右视点均为GB失真的对称失真图像,从该图像的BSSIM可以看出,当左右视点图像均为GB 失真图像,且两个视点图像的失真程度较为接近时,其BSSIM 在视觉上呈现出模糊失真的特性。从图5(b)所示的左视点为无失真图像、右视点为WN 失真图像的BSSIM中,可以很容易地观察到白噪声对图像结构特性的改变。图5(c)(d)所示的是左右视点图像分别为不同类型失真的非对称失真情况,从图5(c)的BSSIM可以明显地观察到JP2K 的压缩效应和模糊造成的图像细节信息的损失带来的叠加效应,相似地,从图5(d)中的BSSIM 也能够观察到压缩效应和噪声同时对图像结构施加的影响。

图5 IVC-II数据库中非对称失真立体图像及其BSSIMFig.5 Asymmetrically distorted images and their BSSIM in IVC-II database((a)GB-GB distortion;(b)REF-WN distortion;(c)JP2K-GB distortion;(d)JP2K-WN distortion)
上述分析表明,BSSIM 能够较好地描述对称失真与非对称失真立体图像左右视点图像之间的结构上的不同,同时能够体现不同失真类型视点图像组合在一起时产生的双目视觉影响,适用于度量立体图像多种失真类型的特性。本文利用BSSIM 的前三阶图像矩,包括均值μB、标准差σB和偏度SB,作为立体图像的双目差异特征的补充。
2.3 图像质量预测模型
为了预测立体图像的质量值,需要训练基于SVR的特征—质量预测模型。用于训练预测模型的特征包括:1)从左右视点图像的HSV 彩色空间和灰度空间中提取的融合特征fc和fg,共39维;2)由左右视点图像的信息熵、标准差和图像质量衰减系数计算得到的双目差异特征(DE,Dv,Dd),以及从左右视点图像的BSSIM 中提取的双目差异特征(μB,σB,SB),共6 维。训练SVR 特征—质量映射模型时基于LIBSVM(Chang 和Lin,2011)软件包,采用Epsilon-SVR模型以及径向基核函数。
除了训练图像质量预测模型之外,本文还利用所提取的左右视点图像之间的双目差异特征(μB,σB,SB,DE,Dv,Dd),共6 个特征,训练基于支持向量分类(support vector classification,SVC)的特征—分类模型,用于判别失真立体图像是对称失真图像还是非对称失真图像。训练SVC 模型时,使用LIBSVM软件包的C-SVC多分类模型,核函数使用径向基核函数。
3 实验结果与分析
为了测试本文算法的性能,在4 个立体图像质量评价测试数据库LIVE 3D IQA Database Phase I(LIVE-I)(Chen 等,2013b)、LIVE 3D IQA Database Phase II(LIVE-II)(Moorthy 等,2013)、IVC-I和IVC-II数据库上进行测试。LIVE-I 是对称失真数据库,包含365 幅图像。其余3 个测试数据库均为对称与非对称失真混合数据库,其中LIVE-II 包含360 幅图 像,IVC-I 包 含330 幅图像,IVC-II 包 含460 幅图像。
测试指标包括立体图像质量预测值与立体图像的DMOS(differential mean opinion score)或MOS 之间的Spearman 等级相关系数(Spearman rank ordered correlation coefficient,SROCC),Pearson 线性相关系数(Pearson linear correlation coefficient,PLCC)和均方根误差(root-mean-squared error,RMSE)。
对比算法选取经典的2D 无参考算法DIIVINE(distortion identification-based image verity and Integrity evaluation)(Moorthy 和Bovik,2011)和BRISQUE(blind/referenceless image spatial quality evaluator)(Mittal 等,2012)、3D 全参考算法CIFR、Lin(Lin 等,2017)、IWSSIM(information content weighted SSIM)(Wang 和 Li,2011)、IDWSSIM(Wang 等,2014)和3D无参考算法SINQ(Liu 等,2017)、Ma(Ma 等,2018)、Yue(Yue 等,2018)、Yang(Yang 等,2019)、Chen(陈勇 等,2021)等。实验中,2D算法分别从左右视点图像中提取单目图像特征,然后串接为一个特征向量,用于训练SVR预测模型。
硬件测试平台使用Intel i7-6280HQ、2.7 GHz 的CPU,内存为16 GB,软件编程环境为MATLAB 2018b。
3.1 算法的准确性与一致性
首先,对比各算法在4 个测试数据库上的预测准确性与一致性。测试时,将各测试数据库随机分为两部分,将包含80%图像的部分作为训练集,剩余20%的图像作为测试集,两个子集中的图像无重复,比较各算法1 000 次测试的SROCC、PLCC 和RMSE 的中值。本文算法与对比算法在LIVE-I、LIVE-II和IVC-I、IVC-II数据库上的实验结果分别如表1和表2所示。

表2 各算法在IVC-I和IVC-II数据库上的比较Table 2 Comparation of performance indexes of each SIQA method on IVC-I and IVC-II databases
从表1和表2可以看出,2D无参考算法DIIVINE和BRISQUE 性能在LIVE-I 和LIVE-II 数据库上的评价准确性较好,但2D算法在评价时没有考虑任何双目视觉特性,在包含左右视点图像失真类型不同的非对称失真图像数据库IVC-I 和IVC-II 上的性能明显较低。本文算法和SINQ 算法在4 个数据库上均取得了最好的评价准确性。本文算法在采用双目竞争视觉特性的基础上,还考虑了非对称失真图像左右视点之间的差异特性,在3 个包含非对称失真图像的数据库上的SROCC 和PLCC 均在0.95 以上,RMSE 也是所有对比算法中取值最低的,优于SINQ算法。在LIVE-I 数据库上,其包含的失真图像均为对称失真图像,左右视点之间的差异较小,各图像之间的差异性特征区分度不大,因此本文算法在评价LIVE-I 数据库中的图像质量时,准确性略微低于SINQ算法的准确性。
图6 进一步给出了本文算法在4 个测试数据库上的预测结果与图像主观评价值DMOS 或MOS 值的散点图来说明本文算法预测值与人类主观评价结果的一致程度。测试时,将测试数据库随机分成训练集和测试集两个部分,训练集包含数据库中80%的图像,测试集包含数据库中其余20%的图像,测试集和训练集中的图像无重复。使用训练集中的图像训练预测模型,并预测测试集中图像的质量,利用5次实验的测试结果绘制散点图。从图6可以看出,本文算法在各数据库上的散点分布均匀,散点的聚集性较高,进一步说明本文算法的预测结果与人类主观评价的一致性高。

图6 本文算法预测值与人类主观评价值散点图Fig.6 The scatter plots between DMOS/MOS and the predicted quality of the proposed method on 4 databases((a)LIVE-I;(b)LIVE-II;(c)IVC-I;(d)IVC-II)
3.2 不同特征对算法性能的贡献
本文算法通过计算左右视点图像的图像质量衰减系数融合左右视点的图像特征,并结合两视点之间的差异特征实现立体图像质量的预测。为了详细了解双目融合特征和双目差异特征对图像质量预测结果的影响,进一步采用本文算法所提取的部分感知特征训练评价模型,比较使用不同特征时算法在4个数据库上的性能。第1种方式,将从左右视点图像中提取的灰度空间和HSV 彩色空间特征串接在一起,构成的特征向量长度为78,所训练模型记为M1;第2种方式,将从左右视点图像中提取的单目图像特征求均值,得到长度为39 维的特征向量,所训练模型记为M2;第3 种方式,利用图像质量衰减系数,将从左右视点中提取的单目图像特征融合在一起,构成长度为39 维的特征向量,所训练模型标记为M3;第4 种方式,使用本文算法提取的所有特征,即在双目融合特征之后串接双目差异特征,记为M4。在表3 中给出上述4 种方式下算法的预测结果。测试时采用3.1 节提到的数据分配方式,重复1 000次相同的实验。

表3 使用不同特征的本文算法在4个测试数据库上的性能比较Table 3 Comparation of performance indexes of the proposed method using different features on 4 databases
从表3 可以看出,在LIVE-I 数据库上,M1、M2、M3 和M4 的评价准确性相差不大,4 种方式的SROCC 和PLCC 都达到了0.95 以上,RMSE 的取值在4.4 左右,相对来说,使用基于融合系数获取的双目融合特征的M3 和M4 方法能够取得较优的评价结果。但是,由于LIVE-I 数据库仅包含对称失真图像,左右视点图像之间的差异很小,所以加入双目差异特征的M4 方法相较于M3 方法不能更进一步提升预测的准确性。在非对称失真图像测试数据库上的实验结果表明M4 方法在LIVE-II、IVC-I 和IVC-II数据库上的评价结果最优,其SROCC、PLCC 和RMSE 明显优于其他方式。尤其是在包含了左右视点失真类型不同的复杂非对称失真图像的IVC-I 和IVC-II 数据库上,M4 方法的性能较其他3 种方法有明显的提升。相对来说,使用双目融合特征的M2和M3方法较M1方法的性能更优。使用融合系数融合两个视点的图像特征的M3 方法性能较采用左右视点图像特征均值的M2方法性能更好。
由上述实验结果可知,在包含了多种复杂的非对称失真图像的测试数据库上,使用基于图像质量衰减系数生成的双目融合特征以及两个视点图像之间的双目差异特征,能够更准确地描述图像的失真特性,有助于提升非对称失真立体图像的评价准确性。
3.3 执行时间比较
算法的执行效率也是评价SIQA 算法性能的重要指标之一。本文以LIVE-II 数据库中的330 幅失真图像为测试对象,统计各算法预测图像质量值或合成转换图像与提取特征的平均时间。仅对比部分已知执行时间的算法。由于2D 算法BRISQUE 只需对左右视点图像的质量求均值,无需计算质量融合系数,其所需的执行时间相对最短,为0.071 s。而CIFR 算法和SINQ 算法在融合图像权重系数计算方面需要对图像进行Gabor 滤波变换或可控金字塔变换,耗时较高,花费的特征提取时间分别为16.485 s和4.149 s。而本文算法在特征融合权重系数计算方面,只需计算图像的信息熵和标准差,所提取特征也无需对图像进行复杂变换,因此提取特征的时间仅需要0.406 s。相对来说,本文算法在3 个非对称失真立体图像测试数据库上的评价准确性稍优于对比算法中性能最好的SINQ 算法,但所需的特征提取时间仅为SINQ 算法的1/10,说明本文算法具有更好的实用性。
3.4 立体图像的非对称性检测
本文利用左右视点图像之间的双目差异特征训练能够用于区分对称失真与非对称失真立体图像的SVC 分类模型。为了验证该模型的分类准确性,在LIVE-II、IVC-I 和IVC-II 这3 个非对称失真数据库上实验。LIVE-II 数据库包含2 种类型失真图像:对称失真图像和左右视点失真类型相同但失真程度不同的非对称失真图像。IVC-I和IVC-II数据库中包含4种类型失真图像,RD 表示一个视点图像为未失真图像、另一个视点图像为失真图像的非对称失真图像,DL 表示左右视点图像的失真类型相同但失真程度不同的非对称失真图像,DD表示左右视点图像的失真类型不同的非对称失真图像。图7 为本文提出的分类模型在3 个非对称失真数据库上1 000 次相同实验的分类混淆矩阵。分类实验时,随机抽取测试数据库中80%图像作为训练集,剩余20%图像用于建立测试集,训练集和测试集中无重复图像。

图7 对称失真与非对称失真图像分类模型在非对称失真数据库上的分类混淆矩阵Fig.7 Confusion matrix for the classifier of symmetrically distorted and asymmetrically distorted images on asymmetrically distorted image databases((a)LIVE-II;(b)IVC-I;(c)IVC-II)
从 图7(a)可以看出,LIVE-II 数据库中有95.46%的非对称失真立体图像能够被准确分类,仅有4.54%非对称失真立体图像被错分为对称失真图像,其原因是当左右视点图像的失真程度近似时,左右视点图像之间的双目差异较小,不容易被区分。此外,LIVE-II 数据库中有10.09%的对称失真图像被分类为非对称失真图像,其原因是LIVE-II数据库中包含FF 失真图像,该类型失真是JP2K 压缩图像经过传输网络随机丢包后生成的,当左右视点图像的压缩程度相同但传输网络丢包的数据不同时,两个视点的结构信息会有明显不同,因此容易被划分为非对称失真图像。
从图7(b)(c)可以看出,在IVC-I和IVC-II数据库上,对称失真图像的分类准确性分别达到了94.76%和98.97%,只有少数图像被错分为左右视点失真类型相同、失真程度不同的DL类型图像。对于左右视点图像失真类型不同的DD 型失真图像,IVC-I 和IVC-II数据库上的分类准确性均分别达到了99.09%和95.32%,说明此类图像的左右视点之间的信息熵、标准差、图像质量衰减系数、结构特征等差异较为明显,用这些特征能够准确描述图像的失真特性。相对来说,RD类型图像和DL类型图像的分类准确性稍低,仅有90%左右,RD 类型图像容易被错分为DL类型,而DL类型的图像容易被错分为对称失真图像,其原因主要在于当两个视点图像之间的失真程度差异较小时,左右视点之间的信息熵、标准差、图像质量衰减系数、结构特征等的差异也会较小,容易被错分为对称失真图像。总体来说,本文利用左右视点图像之间的双目差异特征能够较准确地实现对称失真立体图像与非对称失真立体图像的分类。
4 结论
本文旨在提升非对称失真立体图像质量的评价准确性,提出一种基于双目竞争视觉现象的无参考非对称失真立体图像评价方法。首先,基于人类视觉系统的双目竞争现象,计算左右视点图像的图像质量衰减系数,判别左右视点对立体图像总体质量的影响程度,进而生成两个视点图像特征的融合系数,融合单目图像特征。其次,通过加入左右视点图像之间的在结构等方面的双目差异特征,进一步提升非对称失真立体图像质量感知特征的描述能力。实验结果表明,本文算法提取的特征维数少,特征提取速度快,提高了非对称失真立体图像质量预测的准确性,对多种类型非对称失真图像的质量预测鲁棒性好。此外,本文利用左右视点图像之间的双目差异特征建立的分类模型,能够有效区分对称与非对称失真立体图像,分类准确性高。
本文方法在一定程度上解决了非对称失真立体图像的评价准确性,但特征提取方法还是基于传统的统计特征提取方法,没有结合深度学习方法。后续工作中,如何将本文提出的融合特征方法与深度学习方法结合,进一步提升评价模型对更多种失真类型非对称失真立体图像的普适性,是重要的研究方向。
