基于KDTree改进的Super-4PCS+ICP算法在点云配准中的应用研究
2023-10-24夏军勇高睿杰
夏军勇,高睿杰,钟 飞
(湖北工业大学机械工程学院,湖北 武汉 430068)
1 引 言
点云配准是三维模型重建的关键环节。在工程实际测量中,安装在扫描仪内部的相机角度固定不动,要想获得待测物体完整的点云数据,需要多次转动不同的角度扫描,其中不同视角多次扫描就是点云配准的过程,用最精确的点云配准算法,对多个视角下获得的不同点云片段进行配准处理[1]。从二十世纪末期开始,国外研究人员对点云配准技术做了大量的实验研究,最开始配准的是图像,现在主要是配准三维点云数据。
早在20世纪90年代,国外学者就将四元数求解矩阵的思想运用到点云配准上,提出用四元数法进行点云配准实验[2]。Besl[3]在1992年提出了最近点迭代算法ICP,这个算法至今还是使用最多、应用最广的算法。Chen[4]的改进方法是将两个对应点切平面的距离来代替直线距离,这样就可以让点云重叠区域变多,成功实现了两块点云的配准。文献[5]提出了一种基于法向量与其K近邻法向量夹角不变特征的点云配准方法,可以加快点对应关系的选择。2010年,文献[6]用最小二乘法匹配重叠曲面,先估计局部和模板坐标系的刚体变换参数。Milos Prokop提出用KDTree结构来提高搜索效率,用四元数法和最小二乘法计算配准结果,这个方法明显提高了配准的速度和精度[7]。朱延娟等提出将曲率相似约束条件应用到对应点的构造中,成功实现了配准[8]。储珺等利用二维SIFT提取特征点实现点云配准,这个方法可以有效排除无效数据的影响[9]。
针对于传统的点云配准在配准精度上还是不能达到一些高精度设备的要求。Super_4PCS算法常用于粗配准,ICP算法常用于精配准,本文将对Super_4PCS算法和ICP算法进行改进,通过对点云数据进行“先粗后精”处理,提高点云数据的配准精度。本文提出的“先粗后精”点云配准流程图如图1所示。

图1 点云配准流程
2 点云粗配准
对于需要进行配准的两片初始扫描点云,获取手法及方式的差异会导致它们的初始位姿区别很大。而点云精配准的前提是两片点云初始位姿良好,故在精配准前需要进行粗配准[10],使两片点云的初始位姿大致对齐。粗配准使用的算法是基于随机采样一致性思想,其中使用比较多的就是SAC-IA[11]算法以及Super-4PCS[12]算法。
2.1 Super-4PCS算法
4PCS是将同一个平面内的四点作为基本单位点来寻找对应点,然后进行RANSAC迭代。其原理是根据同一平面内四点之间的仿射不变关系来确定对应点。假定其共面的四点B={a,b,c,d}可以确定满足下列关系的两个仿射不变量r1和r2:
(1)
(2)
得到了两个仿射不变量后寻找对应的四点集,取目标点云里面的任意两个点,计算可能会存在的交点e1,e2:
e1=q1+r1(q2-q1)
(3)
e2=q1+r2(q2-q1)
(4)
假如任意选取的一对点所计算出来的e1与另一对点计算出来的e2近似相等,如下图3所示,就可以确定这两对点之间构成的四点集U1是和基B对应的一个四点集。而对于刚体而言,刚体变换时对应点对之间的距离保持不变,故在点云旋转平移变换过程中四点集还应该满足下式条件:
(5)
(6)
Super-4PCS算法降低了4PCS的计算复杂度,该算法通过角度的约束手段减少了4PCS算法中无效对的产生。同时采用了一种栅格化的方法,将计算距离的二次复杂度降低了,从而极大地提高算法的效率。
2.2 基于KDTree树改进的Super-4PCS点云粗配准
本文点云数据由三维激光扫描仪FreeScan_UE自动扫描轮廓获得,数据量很大,在对点云处理过程中会耗费大量的时间,极大地影响了点云配准的效率。故本文先对扫描得到的数据进行去噪处理,在保留特征点的前提下进行点云精简,极大地减少了点云数量。然后提出KDTree树搜索对应点,结合提取特征点[13]方法对点云的粗配准进行改进,解决计算量巨大的问题。
本文将选取局部区域法向量变化较大的点集来选为特征点集。假定点云区域内的一点pi处法向量的特征度用k近邻点法向量和此局部区域本身的法向量夹角的算术平均值来表示:
(7)
式中,θij是近邻点pj处的法向量与点pi之间的夹角。
选取合适的阈值ε1,因为fi<ε1时会出现局部区域特征不明显的问题,故选取所有fi>ε1的点,而fi<ε1的全部不考虑,去除这不部分无用点。对于其中任意一点pm,若满足:
f(pm)=max[f(pm1),f(pm2),…f(pmk)]
(8)
其中,点pm就被设定为局部区域的一个特征点。
本文改进方法的具体步骤为:
1)对初始散乱点云建立KDTree,加速邻域点的查找。通过三维激光扫描仪获得的点云数据是散乱的,点云的分布没有规律,无法用数学模型来描述,故无法对点云坐标信息进行查询,所以需要建立拓扑信息使得扫描得到的点云数据变得更有规律,从而实现可查询的功能和要求,而KDTree就是建立拓扑关系中应用最为广泛的一种方法。
2)对散乱点云数据按照设置的边长l mm进行分块,使其在边长为l mm的正方形小局部区域内都能获得相应的法向量。
3)通过计算指定的夹角算术平均值得出各分块区域的特征度,并将特征度大于给定阈值的点保留下来。
4)选取任意保留点计算其邻近点的特征度,若保留点的特征度为最大值,则此点即为此局部区域的特征点,直至选完所有的特征点。
5)再使用Super-4PCS算法中的随机采样一致性算法RANSAC进行迭代来确定匹配关系,实现点云粗配准,求解旋转平移矩阵。
2.3 点云粗配准实验及分析
为验证本文方法改进的有效性,本文将在AMD Ryzen 7 2700,机带RAM为16GB的Windows10操作系统上基于MATLAB平台对标准的点云测试实例斯坦福兔点云、龙点云进行算法有效性验证实验。其中源点云为深灰色显示,目标点云浅灰色显示。各实例粗配准实验前初始位姿如图2所示。

图2 粗配准实验前初始位姿
对其使用Super-4PCS算法及本文改进算法进行粗配准,配准后得到的效果图如图3所示。

图3 粗配准结果
本文方法成功完成了源点云与目标点云的粗配准。兔点云和龙点云的点云数据残缺较大,轮廓特征不明显,粗配准效果一般。但相对于Super-4PCS算法,明显可以看出本文方法配准效果更优。
Super-4PCS与本文方法的粗配准实验数据结果如上表1所示,分别列出了粗配准时间、粗配准误差。从表中可以看出,两种方法在配准时间相差无几的情况下,应用本文方法的两个实例两片初始点云已经大部分重叠,成功实现了源点云与目标点云的粗配准,且配准误差相对于Super-4PCS算法明显降低,配准精度有所提高。本文方法对标准数据库实例斯坦福兔点云进行点云配准时,其配准精度相对于Super-4PCS算法最大提高了38.71 %,而龙点云的配准精度提高了11.8 %。数据证明本文改进方法的可行性。满足后续使用精配准算法对于初始位姿的要求。
3 点云精配准
上一节介绍了两片散乱点云的粗配准,从实验结果可以看出,散乱点云经过粗配准后,两片点云的初始位姿发生了很大变化,距离变近,方向对齐,基本实现重叠。但是对于初始位姿很差的点云,错位等问题依然存在,粗配准的精度还远远达不到我们的要求。故在此基础上需要进行精配准来提升配准精度。
3.1 ICP算法
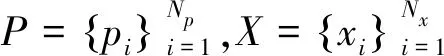
(9)
然后求解使得上述误差函数值最小的刚体变换向量q=[qR|qR]T,记作(q,d)=ϑ(P,Y),上式中d为相应的均方误差函数,即d=f(q)。算法将求解得到的刚体变换作用到第一片点云数据上,记作q(P)。ICP算法迭代地进行该操作直到满足某一设定的收敛准则。
3.2 基于KDTree树改进的ICP点云精配准
1)减少无用点集,本文在进行实验之前,用三维扫描仪获取点云时,会将旁边环境物刷漆涂黑,使周围物体不被扫出,避免出现不必要的噪声点。
2)对应点的选择采用的是KDTree结构搜索欧式距离最小的点。匹配点是选择源点云中与其欧式距离最近的点,设定距离阈值,剔除错误点对。因为经过粗配准后的两片点云初始很近,不需要再用特征点进行快速匹配,而使用KDTree临近查找可以极大地提高搜索效率。
3)点加权采用所有点对常数加权均匀分配,并取权值为常数1,因为本文精确配准之前使用了粗配准,初始位姿保持极好,使用常数为1的加权可以满足条件且便于计算。
4)去除算术平均值以下的错误点对,只保留处于阈值范围内的对应点。误差函数选取点到面的距离平方和。
5)将目标误差函数最小化采用自适应阈值的方式,去中心化后对斜方差矩阵进行SVD分解[14]和ICP算法计算[15-17],求解当前旋转矩阵和平移向量的误差函数是否收敛,若误差函数不收敛,则回到KDTree搜索对应点继续计算,直至迭代收敛,算出最后的旋转平移矩阵。
其中,SVD分解具体原理如下所示为:
对于任意的矩阵A∈Rm×n,存在矩阵U=[u1u2…un]∈Rm×n和V=[u1u2…un]∈Rm×n使得满足:
(10)
式中,∑r=diag(σ1…σn)且σ1≤σ2≤…≪σn。
基于SVD分解改进的ICP算法的计算步骤如下示:
首先计算目标数据点集P和源数据点集Q的重心坐标;
其次计算源数据点集和目标数据点集中点坐标相对于重心坐标的变化量;
(11)
(12)
然后利用其各自的重心变化量构造SVD分解矩阵;
(13)
最后计算旋转平移矩阵。
(14)
R=VUT
(15)
3.3 点云精配准的实验及分析
为验证本文改进的点云精配准方法的有效性和可行性,继续使用标准数据库中的兔点云和龙点云及非标准实例篮球进行有效性验证。其中深灰色点云为源点云,浅灰色点云为目标点云,使用ICP算法和本文改进精配准算法得到的实验结果如图4所示。

图4 精配准后结果
从效果图上看,相较于ICP算法,本文方法对点云精配准的效果更加好。但由于两点云的配准误差非常细微,故对两种方法的实验数据进行统计,作出详细对比,如表2所示。
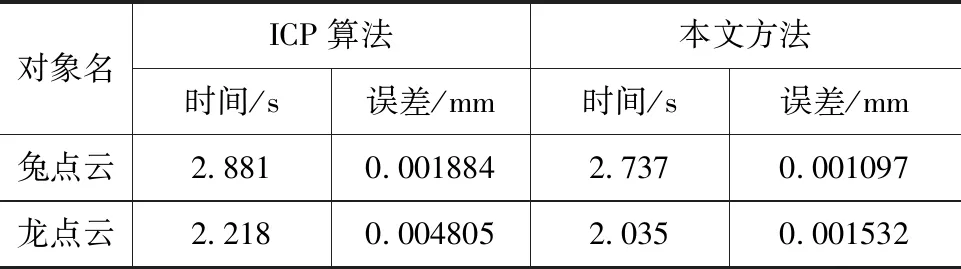
表2 精配准结果数据
由上述可知,本文方法进行精配准后,相较于ICP算法来说配准误差更小,配准精度得到了提高,表明了本文方法精配准的必要性。使用本文方法配准标准例子兔点云和龙点云的精度相对于传统ICP算法精度提高了41.77 %和68.12 %,证明了本文改进方法的有效性。
兔点云旋转平移矩阵为:
龙点云旋转平移矩阵为:
篮球点云旋转平移矩阵为:
4 结 语
本文利用“先粗后精”的思想对两点云进行配准。首先对Super-4PCS算法改进优化,进行粗配准。配准精度最大提高了38.71 %。然后在精配准时用KDTree临近查找,常数加权及对误差函数采用自适应阈值等方法对ICP算法进行优化,分别使用标准数据库和非标准例子进行实验验证,实验结果表明本文方法精配准的效果相较于ICP算法的配准效果有显著提升,配准精度相较于ICP算法最大提升了68.12 %。因此本文的点云配准方法对后期点云模型重建有一定的参考价值。
