基于残差网络的刀具图像超分辨率重建*

崔春蕾,袁德志,朱锟鹏

(1.中国科学院合肥物质科学研究院智能机械研究所,合肥 230031;2.中国科学技术大学,合肥 230026)

0 引言

在机床加工过程中,刀具与加工件之间的高速摩擦会使刀具产生磨损,严重磨损的刀具会降低加工效率和加工精度,故需对刀具的磨损状况进行监测。刀具磨损监测方法可以分为间接法和直接法。间接法是对加工过程中采集的一维信号,例如声信号[1]、振动信号[2]、主轴电流[3]、切削力[4]等,进行特征提取,通过特征值对刀具磨损状态进行监测的方法。然而间接法不能直观监测刀具磨损情况,并且基于深度学习的方法受到训练集数据量的约束,无法满足加工条件多变的情况。

直接法是通过光学相机对刀具切削刃进行拍摄,利用机器视觉方法对刀具图像进行分析的方法。直接法分为两种:传统图像处理法与基于深度学习的方法。前者主要包括边缘检测[6]、阈值分割[7]以及形态学分析[9]等方法。后者利用神经网络对刀具图像进行图像分类[11]以及目标检测[12]等处理。使用直接法对刀具状态进行监测的精确度较高,且不受加工条件的影响。但目前直接法所用图像,是将刀具取下后,使用高分辨率相机进行拍摄。而在实际加工中,由于刀具的高速旋转、微细刀具直径较小以及成本的限制,导致获取的图像分辨率较低。因此直接使用低分辨率图像进行刀具磨损进行监测,会降低监测的准确度。

超分辨率重建方法可以建立高低分辨率图像对之间的关系,可以用于刀具图像,将低分辨率图像重建为高分辨率图像。超分辨率重建方法可分为3类:基于插值、基于建模和基于深度学习的方法。基于插值的方法如双三次插值方法,实现简单,但重建效果较差。基于建模的方法[13],其效果比插值法好,但方法复杂,且需要较多的计算资源。基于深度学习的方法是目前最常用的方法。DONG等[14]构建了用于超分辨率重建的卷积神经网络SRCNN(super-resolution convolutional neural network)。DONG等[15]还提出了利用反卷积层的快速超分辨率卷积神经网络FSRCNN(fast super-resolution convolutional neural networks)。KIM等[16]提出了学习全局残差映射的超分辨率卷积神经网络VDSR。目前基于深度学习的方法主要针对自然图像或人脸图像的特点进行超分辨率重建。然而刀具图像本身具有自己的特点,其纹理较多,且刀具边缘信息是超分辨率重建的重点。

为获得高分辨率刀具图像,本文以微细铣刀为例,提出一种基于残差网络的超分辨率重建方法。为了加强对图像边缘的重建效果,本文提出一种加入边缘信息的图像边缘损失函数对网络进行训练。对不同测试集的重建结果表明,本文网络在客观图像质量评价指标和主观评价上,较双三次插值以及典型超分辨率网络均有所提升。

1 基于卷积神经网络的超分辨率重建方法

1.1 相关工作

相较于插值和重建的方法,基于深度学习的方法可以直接学习高低分辨率图像之间的映射关系,无需对图像进行较多的预处理。DONG等[14]在研究了YANG等[13]提出的基于稀疏编码的超分辨率方法后,将其重建过程等效为一个具有3层卷积层的超分辨率卷积神经网络,网络层次越深,重建效果不一定越好。但KIM等[16]却提出了相反的意见,认为网络深度是影响重建效果的因素之一,故提出了拥有更多卷积层层数的VDSR网络。

VDSR的网络结构如图1所示。在图1中,ILR为LR图像的Y通道,经过双三次插值放大后的ILR表示为Y,IHR为重建得到的高分辨率图像,Conv(fi,ni,ci)表示第i个卷积层,fi、ni、ci分别表示每一层所用的卷积核大小、卷积核数量和通道数,D为卷积层数量,D=20,R为残差图像。为了解决网络结构过深导致收敛速度缓慢的问题,VDSR采用全局残差学习,即只学习插值放大后的LR图像与真实图像之间的残差。插值放大后的图像Y经过D次的卷积操作后,得到残差图像R,残差R与图像Y相加,得到重建的HR图像IHR。第一层卷积层对输入图像进行特征提取,最后一层卷积层则利用特征图重建图像,故f1=fD,c1=cD,n1=nD,中间的卷积层对特征进行非线性映射,其使用的卷积核都是相同的大小和数量,即fi=3、ni=64、ci=64,其中i=2,3,…,19。每个卷积层的计算可简化为:

图1 VDSR网络结构

F1(Y)=max(0,W1*Y+B1)

(1)

Fi(Y)=max(0,Wi*F1(Y)+Bi)

(2)

IHR=WD*FD-1(Y)+BD

(3)

1.2 本文网络

针对刀具图像的超分辨率重建问题,VDSR仍存在训练过程出现梯度爆炸,训练集较小时出现过拟合等问题,故本文在其基础上进行改进。对于卷积神经网络而言,网络结构越深,重建效果越好,但过深的网络结构会导致训练速度缓慢,且容易产生梯度爆炸问题。针对这一点,本文网络采用了全局残差与局部残差相结合的方法来解决。另外,由于刀具磨损区域位于图像中的边缘部分,故刀具图像的边缘信息是超分辨率重建的重点。因此本文提出一种图像边缘损失函数,对重建图像和原始图像进行边缘信息提取,将其加入网络训练所使用的损失函数中,从而提升网络对刀具图像边缘部分的重建效果。

1.2.1 网络结构

本文所提出的网络结构如图2所示。本文网络的结构可以分为5个部分:特征提取、收缩、非线性映射以及反卷积。本文无需对输入图像进行插值放大的预处理,可以直接将LR图像的Y通道作为网络的输入,利用卷积层对LR图像进行特征提取。因为本文使用的刀具图像数据集图像数量较少,所以为了在特征提取层尽可能多的提取特征,使用了Conv(3,d,1)的卷积层,其中d为敏感变量,其值大小决定了从LR图像所提取的特征数量。故该部分卷积层可表示为:

图2 本文网络的网络结构

F1(ILR)=max(0,W1*ILR+B1)+α1min(0,W1*ILR+B1)

(4)

式中:ILR为LR图像的Y通道,W1和B1分别为第一层卷积的权重和偏置,*为卷积运算,α1为激活函数的负向斜率。本文网络使用的激活函数为PReLU激活函数f(x)=max(0,x)+αmin(0,x),该函数可以避免ReLU函数的“神经元死亡”问题。

在上一层对LR图像进行特征提取后,由于特征维度较高,这会导致之后的卷积层训练速度变慢甚至会增大过拟合现象出现的可能性, 故对高维特征进行降维收缩。将该层卷积层设置为Conv(1,s,d),其中s为敏感变量,其值决定了收缩后的特征维度。该部分的卷积层可表示为:

F2(I)=max(0,W2*F(ILR)+B2)+
α2min(0,W2*F(ILR)+B2)

(5)

过深的网络结构可能会导致梯度消失或梯度爆炸问题,网络的训练速度和重建速度也会变慢,甚至会出现“退化现象”[17]。为了避免出现这些问题,并且降低网络的训练难度,本文网络使用了局部残差和全局残差相结合的方法。在这一部分,本文网络使用了HE等[18]提出的ResBlock来实现局部残差,即在卷积层之间增加了跳跃连接,ResBlock的结构如图3所示。

图3 非线性映射部分的ResBlock

ResBlock中的卷积层可以表示为:

Fi+1(I)=max(0,Wi+1*Fi(I)+Bi+1)+
αi+1min(0,Wi+1*Fi(I)+Bi+1)

(6)

Fi+2(I)=max(0,Wi+2*Fi+1(I)+Bi+2)+
αi+2min(0,Wi+2*Fi+1(I)+Bi+2)+Fi(I)

(7)

式中:i的取值范围为i=2,3,…,2+m,m为ResBlock的数量,其数值决定了本文网络的深度。

在收缩层对特征维度进行收缩后,还需要利用扩展层将特征维度进行扩展。DONG等[15]认为,直接利用低维特征进行超分辨率重建,重建质量会比从高维特征中重建的要差,故需要将低维特征扩展到高维再进行超分辨率重建,用于扩展的卷积层可设置为Conv(1,d,s)。该部分卷积层可表示为:

Fi+m+1(I)=max(0,Wi+m+1*Fi+m(I)+Bi+m+1)+
αi+m+1min(0,Wi+m+1*Fi+m(I)+Bi+m+1)

(8)

在网络最后使用反卷积层对图像进行上采样重建。对图像进行步长为k的卷积操作,输出图像的尺寸会变成输入的1/k。而反卷积可以视为卷积的逆操作,在反卷积层中,当步长为k时,输出图像就变成输入的k倍,所以利用反卷积层对图像进行放大重建,反卷积操作的步长k即为重建图像的放大倍数。反卷积层其实是对一组上采样卷积核进行学习。将反卷积层设置为DeConv(9,1,d),该层也是本文网络结构的最后一层,该层的输出为超分辨率重建后的刀具图像。经实验验证,当d=168,s=36,m=3时,网络重建效果最好。

1.2.2 图像边缘损失函数

典型超分辨率网络例如:SRCNN、FSRCNN与VDSR等,为了提升峰值信噪比(peak signal-to-noise ratio,PSNR),均使用MSE函数作为其损失函数。但MSE函数作为超分辨率卷积神经网络的损失函数存在缺点:由于MSE函数是平方计算,所以其对真实图像和重建图像之间的大误差有强惩罚,对小误差有弱惩罚,忽略了图像内容本身的影响。如果图像中出现纹理或者网格,优化MSE函数则会将该区域平滑。所以,对于具有丰富纹理的刀具图像来讲,将MSE函数作为本文网络的损失函数显然是不合适的。相较于MSE函数,L1函数允许异常值的存在,可以减少在优化过程中将图像中的高频信息平滑的现象出现。对于刀具图像而言,在对其进行超分辨率重建时,需要着重注意的是刀具的磨损区域,而该区域位于图像的边缘部分,如图4所示,所以刀具图像中的边缘信息是超分辨率重建的重点。为了提升网络对图像中边缘信息的重建效果,本文提出了一种图像边缘损失函数,在L1损失函数的基础上中增加了图像的边缘损失。边缘损失的计算为:

图4 直径为0.5 mm微细铣削刀具不同磨损状态的边缘纹理

(9)

式中:r为放大倍数,W和H分别为ILR图像的宽和高,ILR为LR图像,GT为HR图像,F()为超分辨率卷积神经网络,故F(ILR)为超分辨率重建后得到的刀具图像,C()为图像边缘信息提取函数,这里的C()采用的是Canny算子,其阈值参数是根据所使用的刀具图像数据集来确定。综上所述,本文网络所使用的图像边缘损失函数为:

l=(1-λ)×lL1+λ×ledge

(10)

式中:lL1为HR图像和重建图像之间的L1损失,ledge为边缘损失函数,λ为加权系数。

2 实验与结果分析

2.1 实验环境

实验所用的刀具图像采集装置由三坐标调节仪、200万像素工业相机、环形垂直光源、VS-TCH-65远心镜头以及笔记本电脑等组成。实验机床为HSM600U五轴联动高速加工中心,采用铣槽方式的干铣削加工。使用直径为0.8 mm和0.5 mm的硬质合金微铣刀分别对纯铜和钢AISI4340进行铣削加工。为了使刀具能够具有不同的磨损状态,实验设置了多种工况对加工件进行铣削,即改变主轴转速、轴向切削深度、单齿进给量等加工参数。网络模型训练使用的电脑系统为Windows 10,显卡为NVIDIA GeForce GTX 1080,Python版本为3.8,Pytorch版本为1.9.0,CUDA版本为11.1。

实验在不同工况下共采集了186张刀具图像作为高分辨率图像,其中包含29张直径为0.8 mm刀具的图像与157张直径为0.5 mm刀具的图像。因为对刀具图像进行超分辨率重建不受工况的影响,故随机选择直径为0.8 mm和直径0.5 mm的刀具图像各10张分别作为测试集1和测试集2,剩余166张图像作为训练集和验证集,其中训练集包含144张,验证集包含20张。为了增加数据量,对训练集进行了图像增强(即对图像分别旋转90°,180°以及270°),将图像数量扩大了4倍。在真实图像中添加随机高斯噪声以模拟图像采集时的环境噪声,进行3倍下采样后得到LR图像。网络训练阶段设置学习率初始值为0.001,使用余弦退火算法提高Adam优化器的性能。

重建后的图像需要使用图像质量评价方法以判断重建效果的好坏。本实验使用全参考图像质量评价方法:峰值信噪比(peak signal-to-noise ratio,PSNR),结构相似度(structural similarity index,SSIM)以及无参考图像质量评价方法:学习感知图像块相似性(learned perceptual image patch similarity,LPIPS)对重建图像的质量进行评估。为了证明图像边缘损失函数在网络训练过程中的优越性,使用PSNR观察验证集在网络训练过程中的重建质量,PSNR值越大,说明验证集重建质量越好。对于测试集,则使用更能体现图像结构信息的SSIM和LPIPS来衡量,SSIM越接近于1,LPIPS越接近于0,则说明经过超分辨率重建的图像质量越好。

2.2 结果分析

2.2.1 不同损失函数对比

本文针对刀具图像的特点以及为了避免MSE函数作为损失函数所出现的问题,提出了一种加入图像边缘损失信息的函数作为网络训练的损失函数,称为图像边缘损失函数。为了探究不同损失函数对网络重建效果的影响以及确定图像边缘损失函数中参数λ的值,分别使用MSE函数、L1函数以及参数λ不同的图像边缘损失函数对网络进行训练。图像边缘损失函数的参数λ取值范围为0.1～0.9,步长为0.1,选择其中重建结果较好的实验与其他损失函数进行对比。

图5为使用MSE函数、L1函数以及λ=0.3的图像边缘损失函数在网络训练过程中PSNR和Loss值的变化曲线图。由图5左图可以看出,使用图像边缘损失函数以及L1函数进行训练的网络,在验证集上的表现均优于使用MSE函数训练的网络,尤其是使用图像边缘损失函数训练的网络,其在验证集上的表现最好,验证集的PSNR值最高。由Loss值的变化曲线可以看出,由于MSE函数的计算方式为平方,所以相比图像边缘损失函数来讲,其Loss值较小,并且因为MSE函数对于较大的误差会有较大的惩罚,所以其Loss曲线并不平稳,导致在训练过程中的PSNR值变化曲线也有较大的变动。但L1函数和图像边缘损失函数可以避免该现象的出现,从图5可以看出,使用这两种损失函数训练的网络,PSNR和Loss值的变化曲线会相对平稳。

图5 使用MSE函数、L1函数以及λ=0.3的图像边缘损失函数在网络训练过程中PSNR和Loss值

表1为使用不同损失函数训练的网络在0.8 mm刀具图像测试集以及0.5 mm刀具图像测试集上的表现。使用图像边缘损失函数训练的网络实验数据共9组,选择3组在测试集上表现最好的网络进行对比。根据表1可知,使用L1函数训练的网络在各测试集上的表现均比使用MSE函数训练的网络重建效果好,证明了L1函数的优越性。同时从表1中也可以看出,使用图像边缘损失函数进行训练的网络,在两种测试集上的表现也均优于仅使用L1函数的网络。因为本文网络所使用的图像边缘损失函数加入了边缘损失信息,使用该损失函数进行训练,就是在针对图像的高频信息损失量进行迭代优化,尽可能减少超分辨率重建图像与高分辨率图像在高频信息上的误差,故使用本文提出的图像边缘损失函数可以增强网络对图像边缘的重建效果,提高图像质量评价指标。

表1 不同损失函数在0.8 mm刀具图像测试集和0.5 mm刀具图像测试集上的表现

2.2.2 不同网络重建结果对比

为了体现本文网络在刀具图像超分辨率重建上的优越性,选取了双三次插值、SRCNN、FSRCNN以及VDSR等3种典型的超分辨率卷积神经网络与本文网络进行对比实验。SRCNN、FSRCNN、VDSR以及本文网络的网络结构参数如表2所示。

表2 不同网络的网络结构参数

另外,SRCNN、FSRCNN以及VDSR使用与本文网络相同的刀具图像训练集进行网络训练,重建放大倍数为3。不同网络训练过程中PSRN和Loss值的变化曲线如图6所示,测试集重建结果如表3和图7所示。

(a) PSNR值的变化 (b) Loss值的变化图6 不同网络的网络训练过程中PSNR和Loss值的变化

图7 不同网络在不同测试集上的重建效果对比图

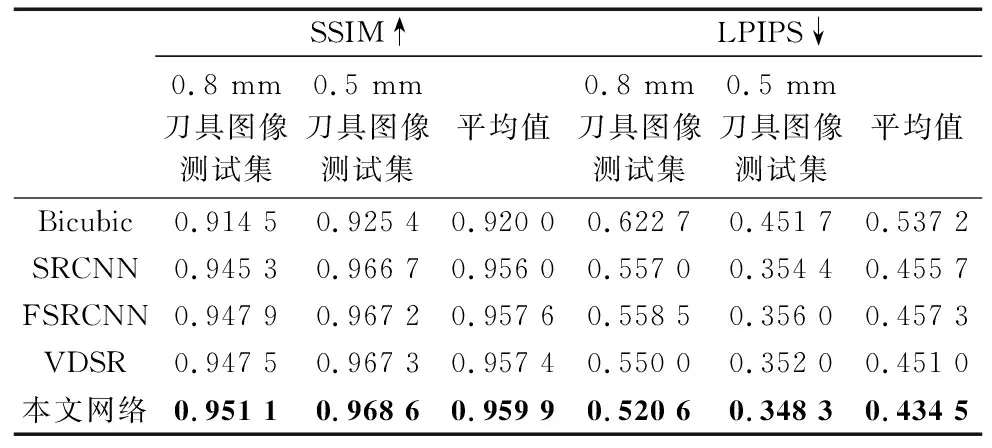
表3 不同网络在0.8 mm刀具图像测试集和0.5 mm刀具图像测试集上的表现

由表3可知,与双三次插值、SRCNN、FSRCNN以及VDSR相比,本文网络在两种刀具图像测试集上的表现均为最佳:在0.8 mm测试集上,SSIM为0.951 1,LPIPS为0.520 6,在0.5 mm测试集,SSIM为0.968 6,LPIPS为0.348 3。因为本文网络在训练过程中使用的是所提出的图像边缘损失函数,而另外3种网络使用的则是MSE函数,故本文网络可以针对刀具图像的边缘重建效果进行加强,故可以提高两种图像客观评价质量指标。

图6a表示不同网络训练过程中PSNR值的变化,图6b表示Loss值的变化。从图6a中可以看出,本文网络在验证集上的表现要优于其他3种网络,其PSNR值明显高于另外3种网络。由于本文网络在训练时使用了余弦退火算法对学习率进行优化以避免陷入局部最小值,而另外3种网络使用的是学习率线性减小的方法,故相比另外3种网络,本文网络在训练过程中的PSNR与Loss值会产生一定的波动,但整体呈收敛趋势。

从0.8 mm刀具图像测试集和0.5 mm刀具图像测试集中分别选择两张不同磨损程度的刀具图像进行超分辨率重建,不同网络对不同测试集的刀具图像的重建效果如图7所示,图7a和图7b为0.8 mm刀具图像,图7c和图7d为0.5 mm刀具图像。从图中可以明显看出,SRCNN与FSRCNN所重建的图像较为模糊,但比双三次插值方法要好。相较于SRCNN与FSRCNN,VDSR网络结构较深,从主观上看,该网络的重建效果明显要比浅层的两种网络重建效果要好。虽然VDSR取得了较好的重建图像,但从图7c和图7d中可以看出,VDSR所重建的0.5 mm刀具图像上出现了“伪影”,即出现了原图所不具有的纹理,这是因为VDSR网络结构过深,出现了轻微过拟合现象,将低分辨率图像中具有的噪声信息也进行了超分辨率,故出现了原图不具有的纹理。而本文网络比SRCNN与FSRCNN深,比VDSR更浅,并且使用局部残差与全局残差相结合的方法来避免过拟合现象的出现,故可以减少超分辨率重建后的图像出现“伪影”。通过对比实验可知,无论在客观图像评价标准还是主观感受上,相比其他典型超分辨率卷积神经网络,本文网络在刀具图像超分辨率重建问题上都有着更好的表现。

3 结束语

本文构建了一种刀具图像超分辨率重建卷积神经网络,并且根据刀具图像的特点,针对MSE函数作为损失函数所出现的问题,提出了一种包含图像边缘信息的图像边缘损失函数,并利用客观图像质量评价指标对超分辨率重建后的两种直径不同的刀具图像测试集进行评价。为了探究图像边缘损失函数对网络的影响以及确定该损失函数中参数λ的值,本文使用不同损失函数对网络进行训练。通过训练过程中验证集在PSNR和Loss值的变化与不同测试集的重建质量,证明本文所提出的图像边缘损失函数相较于MSE函数可以提升网络的超分辨率重建效果,并且通过实验确定图像边缘损失函数中的最佳参数λ=0.3。为了体现本文网络的优越性,与3种典型的超分辨率卷积神经网络进行对比试验。由实验结果可知,本文网络在刀具图像超分辨率重建上的表现,无论在客观评价还是主观评价上均为最佳,在两种不同的刀具图像测试集上,SSIM平均表现为0.959 9,LPIPS为0.434 5,明显优于其他网络。

当前本文只使用了微细平头铣刀的底面图片进行训练与重建,对于其他类型的刀具并没有做更多的泛化性验证实验。下一步将丰富刀具图像数据集,采集结构更加复杂的刀具图像,并在重建速度上对网络性能进行进一步的提升。