考虑行星轮不平衡影响下的啮合边带特征研究*

刘 聪,董惠敏,张 楚

(大连理工大学机械工程学院,大连 116024)

0 引言

行星齿轮传动因具有传动比大、结构紧凑、承载能力强、传动效率高的优点,被广泛应用在汽车、航空航天、船舶和风力发电等领域[1]。行星轮作为传动系统中重要的构件,受安装、材料不均匀因素的影响会产生不平衡故障,在故障的影响下,使得啮合频率及其谐波周围存在大量以故障齿轮特征频率为间隔的调制边带[2],在定轴系统中通常将其作为故障诊断的指标指导工程实践,为此,吸引了很多学者围绕啮合边带调制问题对行星传动系统的故障诊断展开研究。

MCFADDEN等[3]围绕啮合频率周围边带不对称以及啮合频率存在抑制问题展开研究,结果表明这一特征与齿轮箱中行星轮个数、内齿圈齿数有关。随后,INALPOLAT等[4]提出了一种揭示健康状态下齿轮箱边带调制机理的简化振动模型,模型应用汉宁窗函数模拟行星轮转动引起的通过效应,并用该模型对5种不同结构参数的齿轮箱进行分析,揭示了其在正常状态下的边带调制机理。之后模型中又考虑时变啮合刚度和由轮齿交替啮合引起的非线性因素[5],基于该模型对齿轮箱频域特征中由制造误差引起的幅值调制以及相位调制进行研究,同时对其中由行星架转动引起的幅值调制进行解释。LIU等[6]通过建立一种二维集中质量模型,分析振动源到传感器之间传递路径对振动合成信号的影响。LI等[7]对存在稳态、冲击型以及耦合故障的定轴齿轮振动特征进行预测并开展实验,同时研究了共振状态下齿轮箱的振动特征。HE等[8]在传统振动模型的基础上引入测量投影函数,准确模拟单轴传感器的单方向采集特性。LI等[9]在模型[8]的基础上分析不同传递路径下因太阳轮浮动引起的啮合边带特征,揭示太阳轮浮动对啮合边带调制特征的影响。HE等[10]基于LMS建立一种刚柔耦合模型,利用该模型研究太阳轮浮动结构下太阳轮存在轴不对中和轮齿剥落故障时的振动特征,揭示故障状态下的边带调制机理。DANIEL等[11]研究了伺服驱动器中减速器的振动调制特征和制造、装配误差之间的联系,同时揭示运行工况对振动调制特征的影响。

综上所述,学者们在模型简化、健康状态啮合边带调制特征、太阳轮等定轴构件存在某种缺陷时的啮合边带调制机理方面做了很多工作,但鲜见针对具有公转和自转耦合运动特点的行星轮在其不平衡因素影响下的边带特征研究。而不平衡作为行星轮最常见的故障,通过诊断降低其对齿轮箱的影响,对减振、降噪具有重要意义。因此,本文建立了综合考虑行星轮不平衡和太阳轮浮动与时变啮合刚度耦合因素的行星传动系统振动模型,基于该振动模型研究同相位和顺序相位结构特点的齿轮箱在不平衡激励下啮合边带调制机理、特征以及运行工况对啮合边带特征影响,为齿轮箱的故障诊断提供一种参考。

1 振动传递路径与振动模型建立

1.1 振动信号传递路径分析

行星齿轮传动系统中为减少由载荷分布不均引起的振动,齿轮箱中的太阳轮通常采用浮动结构,在与行星轮不平衡产生的横向振动(图1双箭头)耦合作用下,将导致太阳轮向某一方向偏转,使内、外啮合副轮齿不正常啮合,引起啮合力的变化。考虑信号经过轴承以及路径较长时衰减大,以一个行星轮存在不平衡的情况为例,啮合力信号主要通过3条路径传递[6],如图1所示。

(a) 路径1 (b) 路径2 (c) 路径3图1 行星轮不平衡振动信号传递路径

传感器安装在内齿圈上,通常内齿圈与箱体固定,如图1所示。啮合力信号由啮合副到传感器拾振之间存在一定距离,受行星架转动影响,信号传递的路径可分为沿齿圈和齿圈内传递两种形式,其中沿齿圈内的传递,路径长度为常数(图1);另一种沿齿圈传递,不同时刻路径长度不是常数(图2)。因此,每条路径下信号在传递过程中的衰减可分为两种形式:变系数衰减和常系数衰减。

图2 变系数衰减示意图

(1)变路径长度引起的变系数衰减。如图2所示,当行星轮接近传感器时,信号衰减逐渐减小,当行星轮运行到传感器正下方时,衰减最小;行星轮远离传感器时,随着距离的增大衰减逐渐增大,当行星轮运动到传感器对面位置时衰减最大,此时幅值最小。针对行星架旋转引起的变系数信号衰减问题,采用改进的Hanning窗函数(式1)等效。k值越大,啮合频率周围调制边带的分析范围越广,为简化分析,k取1。

(1)

式中:fc为行星架转动频率,a为行星轮距离传感器最远时振动信号幅值衰减系数,ξj、ηj为j阶多项式的幅值、相位。

(2)恒路径长度引起的常系数衰减。信号经过太阳轮或行星轮传递至内齿圈,与信号沿齿圈传递不同,路径长度不受行星架转动影响,即长度是常数。按照对信号衰减的描述,信号在固定距离传递衰减系数为常数。信号在箱体内部的传递(图1)为:

①啮合点n1-内齿圈(路径1)。传感器安装在内齿圈,由内啮合副产生的信号在传递过程中不涉及信号的衰减,因此假设Sr=1。

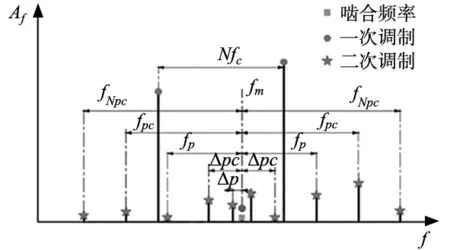
②啮合点n2-行星轮-内齿圈(路径2)。相对情况1的传输距离变长,因此假设0

③啮合点n2-太阳轮-太阳轮轴-太阳轮轴承-内齿圈(路径3)。情况3的传输距离远远大于情况1和2,且经过轴承,因此情况3的信号衰减要远远大于1和3,即Sss<

1.2 齿轮传动系统振动模型建立

为了求解考虑行星轮不平衡因素的啮合力,首先建立齿轮箱的运动微分方程求解系统的广义位移,并依据变形协调关系将广义位移投影到啮合线方向,结合时变啮合刚度得到系统的弹性啮合力,最后在上节传递路径分析的基础上建立系统振动模型。

如图3所示,齿轮采用集中质量点等效,每个质量点考虑x、y、z、θz四个自由度,为简化计算,将绕旋转轴的角位移转化为线位移uz。

图3 行星传动齿轮箱等效模型

根据牛顿第二定律,建立各齿轮运动微分方程,将所有齿轮微分方程按行星架(c)、内齿圈(r)、太阳轮(s)、行星轮(p)顺序组装,系统运动微分方程为:

(2)

(3)

Kw、Ch、Kh分别为系统向心刚度矩阵,轴承支承阻尼阵和支承刚度阵,具体形式为:

Ch=diag[chcchrchs0 0 0]
Kh=diag[khckhrkhs0 0 0]
Kw=diag[mc,mc,0,0,mr,mr,0,0,ms,ms,0,0,mp,…,0]

(4)

式中:chj=diag[cxjcyjczjcuj]和khj=diag[kxjkyjkzjkuj]分别为齿轮构件j(j=c,r,s)的支承阻尼阵和刚度阵。

广义位移和弹性变形在啮合线方向变形协调,将齿轮位移投影到啮合线方向(图4),则内外啮合副-内齿圈(太阳轮)与第i个行星轮之间的弹性变形为:

图4 啮合副相对位移示意图

(5)

式中:ψEi=φi-α,ψIi=φi+α,α为啮合副啮合角,忽略由齿轮中心位移变化引起的啮合角变化;φi为第i个行星轮位置角,φi=2π(i-1)/N+φ1;φ1为第一个行星轮与Xc夹角。

结合时变啮合刚度和啮合副间弹性变形,弹性啮合力可表示为:

(6)

啮合力与传感器的数据采集方向存在一定的夹角(图5),且随着行星架的旋转呈周期性变化。单向传感器只能采集某一方向振动数据,因此需要将啮合力向传感器测量方向投影。基于夹角随行星架转动周期变化,采用周期函数P表示为:

图5 啮合力投影示意图

pI=cos(2πfct-(π/2-α)+φi)
pE=cos(2πfct-(π/2+α)+φi)

(7)

式中:下标I、E分别代表内外啮合。

综上所述,基于传感器采集信号为多路径信号线性叠加假设,系统的振动模型表达为:

(8)

式中:S为固定距离衰减系数,w为变距离衰减系数,P为投影函数,f为啮合力,下标rp、sp分别代表内齿圈(太阳轮)与行星轮组成内(外)啮合副。

2 模型振动影响因素分析

2.1 不平衡力激励的表达

行星轮与定轴转动的转子不同,其运动包括相对行星架的自转以及随行星架的公转,其中对行星轮自转的描述是在行星轮坐标系,而随行星架的公转则在全局坐标系。因此,由不平衡产生的不平衡力在对应坐标系下均存在分量。从单一转子受力角度分析,需要将全局坐标系下的不平衡力统一到行星轮坐标系,以第i个行星轮为例,推导不平衡力分量的函数表达式。

(1)公转半径的表达。在行星轮上施加不平衡质量模拟行星轮不平衡。受行星架公转影响,在全局坐标系下,不平衡质量所在位置随行星架的旋转呈周期变化(图6)。很明显,公转半径变化的周期和行星架转频fc及行星轮转频fp有关,因此公转距离的变化可表示为:

图6 不平衡力分解示意图

(9)

式中:xi=qicos(2πfpt+γ(i))、yi=qisin(2πfpt+γ(i))分别为不平衡质量在第i个行星轮坐标系下的坐标,qi,γi分别为第i个行星轮的不平衡半径和初始相位,rs、rpi分别为太阳轮和行星轮的分度圆半径,rg为公转半径,下标g表示公转。

(2)不平衡力的确定。将公转力向x、y轴投影(如图6),得到公转坐标系下公转力的不平衡力分量,同时进行坐标变换,将公转力转到行星轮坐标系下,对应行星轮坐标系下不平衡力分量的函数表达式为:

(10)

式中:Fg、Fgz分别为全局坐标系下的公转力和行星轮坐标系下的公转力,下标gz代表公转到自转的转换,p=[px;py]为全局坐标系下不平衡质径积,大小为不平衡质量与公转半径乘积。

行星轮坐标系下由行星轮自转产生的不平衡分力为:

(11)

运动微分方程中引入的不平衡力矢量为:

(12)

式中:f为不平衡力在对应自由度上的分量,大小为两个矢量分力的叠加(未考虑轴向尺寸较大引入的力偶分量);下标u代表不平衡。

2.2 时变啮合刚度激励

齿轮啮合刚度变化是导致齿轮箱振动的重要因素。在传动过程中随着单双齿的交替啮合,啮合刚度周期变化,进而引起啮合力的变化。为此模型中考虑啮合刚度变化对啮合力的影响,并基于能量法[12]得到内外啮合副间综合刚度k(式13),结合投影向量[13]得到时变啮合刚度,变化规律如图7所示。

图7 时变啮合刚度

(13)

2.3 太阳轮浮动

太阳轮浮动是实现齿轮箱载荷均匀分配最简单的方法。由于浮动结构(太阳轮径向刚度:kxs=kys=0),行星轮存在不平衡时,太阳轮会受到不平衡啮合力的作用,产生沿合力方向的平动趋势(图8),相对于太阳轮不浮动情况,啮合副间的啮合状态被改变,从而影响整个传动系统的振动。

图8 太阳轮受力图

3 啮合边带调制特征仿真分析

为了揭示行星轮不平衡对啮合边带调制特征的影响,以同相位和顺序相位两种结构特点的传动系统为例,首先分析健康状态下齿轮箱振动调制特征,其中齿轮箱初始位置如图8所示,输出转速1500 r/min,负载转矩200 N·m,特征频率和模型结构参数如表1、表2所示,其中以行星架转频为归一化频率。表中括号内数据为同相位结构齿轮箱参数。

表1 行星齿轮箱特征频率 (Hz)

表2 行星齿轮箱模型参数

顺序相位和同相位健康状态下边带特征如图9所示,表明齿轮箱振动特征受内齿圈齿数和行星轮个数影响,当内齿圈齿数不是行星轮个数的整数倍,啮合频率周围不存在调制边带;内齿圈齿数为行星轮个数整数倍,啮合频率处幅值为0,两侧出现以Nfc为间隔的调制边带,振动主要由行星轮通过效应引起。

(a) 同相位 (b) 顺序相位图9 齿轮箱健康状态振动特征

为简化分析流程,在行星轮相位0°位置处施加质径积为600 g·mm的不平衡量,基于建立的振动模型分别研究同相位和顺序相位安装结构的行星齿轮箱单一行星轮和多行星轮均存在不平衡故障时系统的啮合边带调制特征。

3.1 顺序相位结构的齿轮箱

(1)单一行星轮不平衡振动特征分析。假设传动系统中行星轮除安装位置不同,其余参数均相同(表1)。图10为行星轮不平衡故障时振动信号的Fourier频谱。由图可见内齿圈齿数不是行星轮个数的整数倍,以间隔Nfc的边带为主导边带;边带主要集中在fm±kfc±nfp(k,n=0,±1,±2,…)位置处,这些边带频率均和行星轮故障特征频率fp相关。对边带与啮合频率之间间隔进行分析,可以得到行星轮不平衡情况下啮合边带的调制机理,即啮合力首先受到行星架转频调制然后再受到行星轮自转、公转转频调制。在双重调制影响下,出现特殊频率间隔Δp、fNpc,特殊频率阶次如表3所示,该特殊的频率间隔可以用来作为评价齿轮箱存在故障的指标。

图10 单行星轮不平衡啮合边带特征(顺序相位)

表3 相对归一化频率特殊阶次边带(顺序相位)

(2)多行星轮不平衡振动特征分析。不平衡参数同情况一。对齿轮箱中2个和3个行星轮均存在不平衡情况分析,Fourier频谱如图11所示。

(a) 双行星轮不平衡

(b) 三行星轮不平衡图11 多行星轮不平衡啮合边带特征(顺序相位)

相对于单个行星轮不平衡,多个行星轮存在不平衡时fpc边带幅值占主导地位,说明行星轮存在不平衡时可能造成不均匀的行星架载荷分配,使得行星架旋转运动对啮合振动的调幅作用进一步加大,即对应边带分量幅值增加,齿轮箱振动增大。特殊的是3个行星轮均存在不平衡时,系统中仅保留与啮合频率间隔为fpc的边带分量以及特殊频率间隔Δp、fNpc,而与之相对的fp及其余边带分量的幅值均在原来基础上被抑制。

多个行星轮不平衡情况下的调制机理与单个行星轮的调制机理相同,而由于顺序相位安装结构中行星之间的相位角不同,导致3个行星轮不平衡情况下振动幅值矢量叠加后为0;3个行星轮存在相同不平衡时,由于浮动设置,在啮合力作用下,太阳轮将呈现近似三角形运动(图12所示,由于顺序相位结构存在啮合相位差,故同一时刻啮合刚度不同)。

图12 太阳轮中心轨迹(顺序相位)

(3)运行工况对不平衡振动调制特征影响。研究不同工况对振动调制特征的影响,为此分析输出转速为600 r/min、900 r/min、1200 r/min、1500 r/min等4个转速以及10 N·m、50 N·m、100 N·m、150 N·m、200 N·m负载下传动系统的啮合边带特征。运行环境发生变化时,对于强度信号,边带与主频的幅值比相对稳定,因此通过边带主频幅值比即主频边带累积量与主频幅值的相对比值来衡量振动的变化(式13),以一个行星轮存在不平衡为例分析。结果如表4所示,表明在相同运行条件下边带特征在高转速、低负载时,故障特征明显;低转速和高负载情况下缺乏明显特征,但是应注意,随着运行环境变化,不平衡带来的边带累积量会发生突变,代表齿轮箱在运行环境发生变化后产生了剧烈的冲击。

表4 不同工况顺序相位结构齿轮箱边带主频幅值比

(14)

式中:fd为主频边带幅值。

3.2 同相位结构的齿轮箱

(1)单一行星轮不平衡振动特征分析。分析步骤同顺序相位,不再赘述。结果表明同相位结构中内齿圈齿数为行星轮个数整数倍,啮合频率为主导频率;边带主要集中在fm±kfc±nfp(k,n=0,±1,±2,…)位置处,边带调制机理与顺序相位相同,即啮合力首先受到行星架转动调制,然后再受到行星轮自转、公转转频调制。在双重调制影响下,出现特殊频率间隔边带Δp和fNpc(图13),特殊频率阶次如表5所示,该特殊的频率间隔可以用来作为评价齿轮箱存在故障的指标。

图13 单行星轮不平衡影响下的边带特征(同相位)

表5 相对归一化频率特殊边带阶次(同相位)

(2)多行星轮不平衡振动调制特征分析。不平衡参数与顺序相位相同,齿轮箱中2个和3个行星轮存在不平衡时Fourier频谱如图14所示。

(a) 双行星轮不平衡

(b) 三行星轮不平衡图14 多行星轮不平衡影响下的边带特征(同相位)

相对于单个行星轮不平衡,多个行星轮存在不平衡时fp、fpc边带幅值占主导地位,说明行星轮存在故障,且该故障可能造成不均匀的行星架载荷分配,使得行星架旋转运动对啮合振动的调幅作用进一步加大,即对应边带分量幅值增加,齿轮箱振动增大。特殊的是相对于顺序相位,3个行星轮均存在不平衡时,系统中边带分量fp占主导地位,Δp、fNpc和fpc及其余边带分量的幅值均在原来基础上被抑制。

多个行星轮不平衡情况下的调制机理与单个行星轮的调制机理相同;由于同相位安装结构行星之间的相位角相同,故同一时刻啮合刚度相同,在啮合力作用下,太阳轮受力平衡,其轨迹近似为一个点(图15所示,太阳轮x、y方向振动幅值轨迹变化范围小于2e-15)。相对于存在啮合相位差情况,同相位安装使得传动系统扭转方向的振动增加,径向振动降低,因此在相同情况下通常采用改变齿轮参数的方式降低传动系统的振动。另外由于存在啮合相位,导致了顺序相位和同相位安装结构下3个行星轮存在相同不平衡时(幅值和相位均相同)表现出的振动特征完全不同。

图15 太阳轮中心轨迹(同相位结构)

(3)运行工况对不平衡振动调制特征影响。同理,研究不同工况对同相位安装结构齿轮箱振动调制特征影响,分析输出转速为600 r/min、900 r/min、1200 r/min、1500 r/min等4个转速以及10 N·m、50 N·m、100 N·m、150 N·m、200 N·m工况下传动系统的振动特征。以一个行星轮存在不平衡为例分析,结果与顺序相位表现的特征相似,振动特征对运行环境的变化很敏感,结果如表6所示。

表6 不同工况同相位结构齿轮箱边带主频幅值比

4 结论

基于振动信号传递路径分析,建立了行星传动系统振动模型,仿真分析了同相位、顺序相位结构的齿轮箱在不平衡激励下系统振动特征、边带调制机理以及在不同工况下的振动特征,主要结论如下:

(1)健康状态,内齿圈齿数不是行星轮个数的整数倍时,由于相位矢量叠加,啮合频率处幅值抑制,且在啮合频率两侧会出现以行星轮通过频率Nfc为间隔的边带;整数倍时啮合频率处幅值最大,两侧不存在啮合边带;

(2)行星轮存在不平衡,振动信号首先受到行星架转动引起的行星轮通过效应影响,表现在频域即啮合频率周围存在间隔为Nfc的边带,该间隔会受到齿轮箱安装结构的影响;其次在不平衡引起的横向振动影响下,振动特征受到行星轮自转以及相对转动的影响,表现在频域中即啮合频率周围出现以行星轮自转、公转以及线性组合为间隔的特征频率边带,在双重影响下出现特殊频率分量fNpc、Δp,该频率分量可以用来判断行星轮存在故障;

(3)行星轮不平衡故障对运行工况变化很敏感,对于变工况运转的机械设备,当工况发生变化时必须停机检查,确认无问题时才可继续工作。