多端环型海底观测网供电系统故障主动定位方法

陈宁铤，黄文焘，杨欢红，方世源，余墨多，杨 咏

（1.上海电力大学电气工程学院,上海市 200090；2.电力传输与功率变换控制教育部重点实验室（上海交通大学）,上海市 200240；3.船舶与海洋工程特种装备和动力系统国家工程研究中心,上海市 200030；4.北京特种工程设计研究院,北京市 100028）

0 引言

海底观测网是海洋观测体系中功能最先进的平台之一,可对海洋环境与活动进行全天候连续观测,在生态调查、国防安全和灾害预警等方面都有着显著作用［1］。目前,中国正在快速构建全球海洋立体观测体系,大规模、远距离海底观测网成为其中的关键组成部分。为提高系统可靠性与稳定性,观测网主干网常采用多端环型结构,“海王星”海底观测网采用了双岸基源和三环网冗余结构。由于恶劣的海洋地质环境以及频繁的人类开发活动,海底观测网遭到破坏进而发生故障的事件越来越多,光电复合缆破损与海水接触后直接导致短路故障,给观测网供电系统带来严重威胁［2-3］。更为重要的是,观测网供电系统故障查找困难,不仅费时且成本高,多端环状结构更是增加了故障定位难度。因此,快速、准确地定位故障是多端环型海底观测网亟须解决的关键技术。

多端环型海底观测网采用直流供电的方式,目前已有大量直流系统故障定位的相关研究。文献［4］提出了一种基于主动式行波的故障定位方法,通过脉冲行波定位故障,但受线路类型、过渡电阻等因素影响,存在反射波检测不准的风险。文献［5］在行波法的基础上利用固有频率进行辅助定位,通过经验模态分解得到高频行波分量。该方法所需的固有频率参数由神经网络识别获取,对历史数据的数量与质量要求较高。文献［6］提出一种基于分布参数模型的故障定位方法,通过沿线电压、电流分布,计算并搜索过渡电阻最小值点,确定故障点位置,该方法并未考虑频变参数的影响,对长线路的定位误差较大。

多节点直流供电系统的故障定位方法均需要大量的节点量测数据,难以应用于量测数据有限的多端环型海底观测网供电系统。海底观测网供电系统通过分支单元连接光电复合缆构成,复杂环境使得分支单元不易维护和更换,分支单元弱化了量测元件和通信元件,从而有效提高了主干节点的可靠性和稳定性。但与此同时,系统也无法获取主干节点的电压、电流数据［7］,有限的量测数据一方面使得故障难以有效定位,另一方面分支电流会影响定位算法中线路电压幅值的计算,导致无法确定实际故障位置。同时,现有算法难以有效判定主干分支节点附近的高阻故障,存在定位死区［8-9］。

现有海底观测网供电系统故障定位大多采用阻抗法,具有简单、易实现的优点。但阻抗法通常利用直流稳态数据进行故障定位,因海底电缆上存在分散电感电容,所能获取的有效直流稳态故障信息较少,导致多端环型系统中故障定位实现困难。文献［10］利用岸基站到故障点的基尔霍夫电压方程来计算故障位置,但该方法须计算每条分支电缆的电流值,应用于大规模多端海底供电系统存在计算量大、定位速度慢等问题。文献［11］提出了时域-频域反射法和切线距离模式识别的海缆故障定位方法,但行波检测装置无法有效区分故障所在的环网间隔。文献［12］提出了基于多端故障行波时差的海底观测网故障定位方法,安装同步测量装置,捕捉各节点故障初始行波到达时间并构建时差矩阵,解决了多环网结构对故障定位的影响,但该方法需要在所有分支单元中增设高性能量测装置。文献［13-14］提出了检测相位突变的故障定位方法,在一定程度上改善了分支点附近死区问题,但该方法需要对所有分支进行逐一搜索计算,难以应用于数据有限且存在大量分支的多端环型海底观测网供电系统。

本文提出了一种附加量测节点的多端环型海底观测网供电系统主动故障定位方法。基于多端环型网络结构选择附加量测节点,提出了谐波注入的主动故障定位原理。该原理构建不同故障场景下虚拟故障点,通过虚拟双节点定位方程,判别故障支路并计算故障位置。“海王星”海底观测网系统仿真结果表明,所提方法在不同故障类型下均可实现可靠、准确的故障定位。

1 多端环型海底观测网结构与量测节点

1.1 多端环型海底观测网供电系统

典型多端环型海底观测网供电系统如图1 所示,供电系统主要由岸基站、分支单元、接驳盒和海底电缆组成［15］。其中,分支单元作为系统的主干节点,通过主干电缆与岸基站构成系统主干网,接驳盒则通过分支电缆接入主干网络。由于多端环型海底观测网供电系统规模较大,通常采用单极负高压直流输电方式,在保证供电系统稳定的同时可以降低设备成本并减少输电损耗。

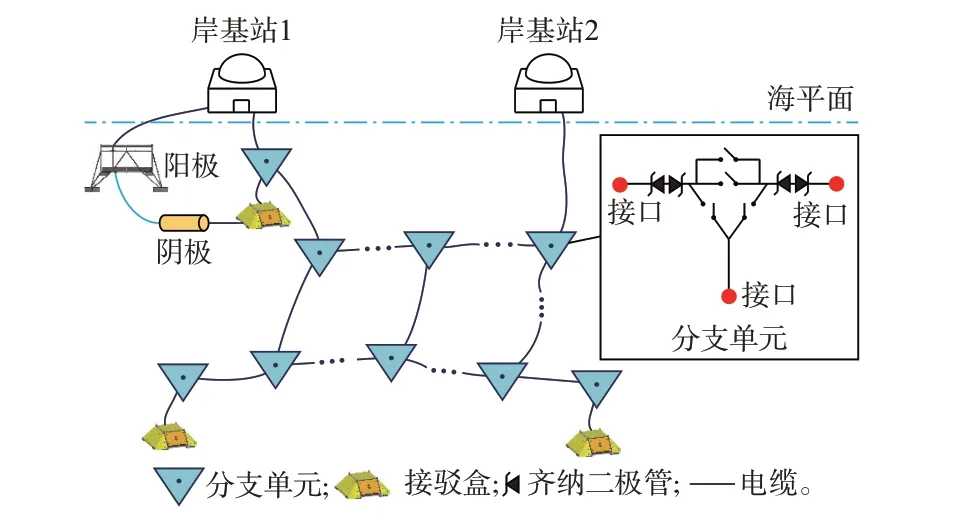
图1 典型海底观测网供电系统Fig.1 Typical power supply system for undersea observation networks

多端环型海底观测网供电系统通常采用双岸基站、-10 kV 高压直流供电。发生故障后可通过另一岸基站供电,大大提高了供电系统的可靠性。接驳盒主要收集数据并控制观测传感器,其内部DCDC 转换器可提供375 V 或48 V 供电接口［16］。每个接驳盒均配备阴极,与岸基站设置的阳极构成海水输电回路。分支单元主要功能为隔离故障电缆,以保证故障时其他电气设备的正常运行。基于实际观测要求,多个分支单元节点可以构成单个或者多个连续环型结构,不仅增强了系统供电能力,也提高了整体可靠性。海缆在海洋和人类活动的影响下容易受到损坏而导致故障,其中发生概率最高且危害最大的为短路故障。由于多端环型结构拓扑复杂,仅利用岸基站数据难以定位故障,需在少量关键节点附加量测装置,实现故障的主动、快速与准确定位。

1.2 多端环型结构的附加量测节点选择

多端环型海底观测网供电系统拓扑结构复杂,且由于简化了主干节点内部的通信元件和量测元件以提高其稳定性和可靠性,导致无法获取主干节点上的电压电流数据。仅根据岸基站量测数据无法实现多端环型海底供电系统的故障定位,因此,需设置附加量测节点以获取故障定位的必要数据。且由于多端环型结构由单独环网和多连环网组成,在环网中发生故障时故障电流双向流动,根据有限量测节点的数据无法确定环网中故障点的具体位置。因此,分解环网结构是确定附加量测节点的基础。如图1 所示,受结构限制,分支单元最多有3 个接口,通常每个节点都会与接驳盒相连。当3 个接口均与分支单元连接时,该节点无法连接接驳盒,仅用于连接主干网络,构成主干网的分支点。

需先对多连环网进行分解,为保证系统中每个节点都能获得可靠供电,应将两岸基站之间最长连通路径作为主要电能传输路径。通过列出两岸基站之间的所有连通路径,并对每一条连通路径的总长度进行比较以确定岸基站间的最长连通路径［17］。选择非最长连通路径上的多连环网相交点作为分解点,以保证分解后的所得分支都与最长连通路径相通,如图2 所示。图中:US为分解点S 的电压,IS1,IS2,IS3分别为分解点S 流向不同分支电缆的电流。

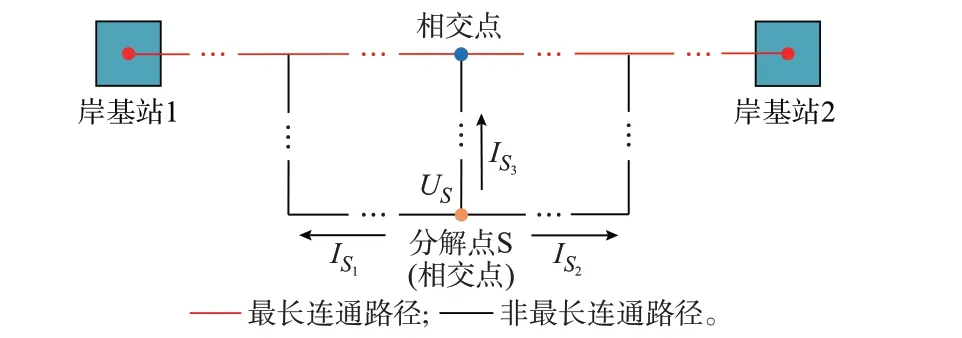
图2 多连环网结构Fig.2 Structure of multi-connection ring network

若多连环网分解后仍存在单个环网,则需确定该环网接入最长连通路径的分支点位置,分别记为C1,C2,…,Cn,根据系统结构和参数,可以获得各分支点到任一岸基站的最短距离,分别为LC,1,LC,2,…,LC,n。选择离岸基站最远的分支点作为分解点,并断开该点与最长连通路径的连接以实现分解。所选分解点S 离岸基站的距离为所有分支点到岸基站距离中的最大值,如式（1）所示。

式中:LS为分解点S 到任一岸基站的最短距离。

在确定分解点后,即可根据分解点所连接支路数量拆分为对应个数的新节点,如图3 中节点S1,S2,S3。分解所得节点为系统中新的末端节点,且与原分解点的电压与电流大小均相同。

图3 多连环网的分解结构Fig.3 Decomposition structure of multi-connection ring network

为了实现整个系统的故障定位,所有环网分解后系统的始端、末端节点都须被选为附加量测节点,即系统中连通数为1 的节点。因环网分解点在完成解环后会在系统中形成新的末端节点,所以环网分解点即为系统中的附加量测节点。连通数为2 的节点在主干网络中仅用于连接各分支点和始末端节点,连通数为3 的节点是主干网络分支点,仅起到连接作用,这两种情况的节点无须获取数据,则可定为非量测节点。

2 主动故障定位方法

2.1 基于谐波注入的主动故障定位原理

通过岸基站变换器向海底观测网供电系统主动注入谐波信号,量测节点获取额外谐波数据,实现故障快速定位［18-19］。岸基站和量测节点统称为计算节点,在如图4 所示的多节点供电系统中,U̇M、U̇N、İM、İN分别为计算节点M、N 的测量谐波电压和电流；LM、LN分别为分支点O 到计算节点M、N 的电缆长度。将各电缆分支进行编号,分别为B1,B2,…,Bk。将计算节点M 和分支点O 之间电缆上一点记为p,点p 的谐波电压和电流可由式（2）—式（3）得到。

图4 多节点供电系统Fig.4 Multi-node power supply system

式 中:U̇p和İp分 别 为 点p 处 的 谐 波 电 压 和 电 流；Lp为从点p 到计算节点M 的距离；ZC为海底电缆的特性阻抗；γ为海底电缆的传播常数。

设故障位于计算节点M 与分支点O 之间,将计算节点M 和N 之间的电缆均匀分段并对分段点进行编号,分别记为1,2,…,D。利用计算节点M 和N的谐波数据分别计算各分段点电压,并将其相应作差,根据最小电压差即可得到故障点位置如式（4）—式（6）所示。

式中:d为某一分段点编号；ΔU̇d为分段点d的计算电压差；dc为最接近故障点的分段点编号；LF为节点M 到故障点F 的距离。

由于分支点P 所对应的非故障支路会向分支点O 注入额外电流,因此,仅根据式（2）—式（6）进行的第1 次电压差搜索只能获得近似故障位置,称为“虚拟故障点”。选择任一计算节点作为参考节点,再选另一个计算节点作为对照节点,其相连电缆支路分别为参考支路和对照支路,除此之外的电缆支路都为旁路。直接利用两计算节点数据计算得到虚拟故障点后,需要利用该点与参考节点或最近分支点进一步构成虚拟双节点方程,从而获取实际故障点位置。根据所选参考支路和对照支路的不同,有以下4 种不同定位场景。

1）故障点位于参考节点和虚拟故障点之间,如图5（a）所示。虚拟故障点和参考节点将用于构建虚拟双节点方程并进行第2 次电压差搜索。由于故障点电压为电缆支路上最低点,且不会再受到分支电流的影响,所以虚拟双节点方程可以进一步搜索计算出实际故障点位置,即该场景下存在虚拟故障点。

图5 不同故障定位场景Fig.5 Different fault location scenarios

2）故障点位于虚拟故障点和最近分支点之间,如图5（b）所示。虚拟故障点和最近分支点将用于构建虚拟双节点方程。与图5（a）场景相似,虚拟双节点方程也不会受到分支电流的影响,可以搜索计算得出实际故障点位置,即该场景下存在虚拟故障点。

3）故障点位于对照支路上,如图5（c）所示。由于虚拟故障点无论与参考节点或最近分支点构建虚拟双节点方程都无法搜索获得最小电压差,电压呈现发散趋势,即虚拟双节点方程无解。因此,该场景实际不存在虚拟故障点。

4）故障点位于旁路上,如图5（d）所示。由于参考支路和对照支路上没有受到故障电流影响,因此计算所得虚拟故障点理论上位于旁路所对应分支点处。考虑到测量误差的影响,实际情况中虚拟故障点可能位于参考支路或对照支路上。根据前3 个场景的结论,可得该场景下可能存在虚拟故障点。

2.2 基于虚拟故障点的主动故障定位方法

对系统中各电缆支路进行编号,并按顺序依次选择两条不同电缆支路作为参考支路和对照支路进行计算,以虚拟双节点方程的计算结果构建判断矩阵。矩阵行坐标对应于所选的参考支路,列坐标对应于所选的对照支路。判断矩阵的秩等于系统电缆支路总数。以附录A 图A1 所示三节点供电系统为例,共有3 条分支分别记为B1,B2,B3。若故障发生在计算节点N与分支点之间,可得到判断矩阵MJ如（7）所示。

式中:DB,q,w为以第q条分支为参考支路、第w条分支为对照支路所构建定位方程的有效解；Δ为表示是否存在有效解的变量,其值为-1 时表示不存在有效解,否则表示存在有效解；矩阵中的元素-1 表示不存在有效解,0 表示无此项。

在多节点供电系统中,判断矩阵基于以下特征来定位故障。

1）当故障支路被选为参考支路时,相应行的元素都为有效解,如式（7）中第2 行所示,可由式（8）表示。

式中:f为故障支路所对应分支编号；y为除故障支路外的某一分支编号,y≠f；MJ,f,y为判断矩阵中的第f行第y列所指元素。

2）当故障支路被选为对照支路时,相应列的非对角元素都为-1,如式（7）中第2 列所示,可由式（9）表示。

式中:MJ,y,f为判断矩阵中的第y行第f列所指元素。

3）所有其他行和列的特征都与式（8）和式（9）的特征不匹配。

基于判断矩阵对故障行所有有效解取算术平均值,以获得精确的故障定位结果,如式（10）所示。

式中:LFA为故障支路对应计算节点到实际故障点的准确距离；R为判断矩阵的秩。

在多节点供电系统中,若所选的两条电缆支路不直接相连,利用上述故障定位方法所得的判断矩阵中对应元素为无效解。若供电系统在拓扑上近似对称,判断矩阵会出现大量无效解,导致故障支路误判。在图4 所示的多节点供电系统中,若环网分解后存在Σ条电缆支路,则可得判断矩阵的秩也为Σ,将各支路分别记为B1,B2,…,BΣ。假设故障发生在多节点供电系统的B3分支上,因除分支B1、B2以外其他分支在拓扑上都没有与B3分支直接相连,使得判断矩阵中非对角元素从第3 列到第Σ列不存在任何有效解,导致无法判断故障位置,如式（11）所示。

为防止判断矩阵失效,需要将所有电缆支路视为直接连接,并相应修改算法。若所选参考支路未直接连接到所选对照支路,则将对照支路的长度修正为参考节点最近分支点到对照节点之间电缆的长度。完成长度校正后判断矩阵将修正为式（12）,与前文所述判断矩阵故障特征式（8）—式（9）完全匹配。

3 主动故障定位流程与实现

利用岸基站换流器的控制能力,周期性产生谐波信号,注入供电系统网络以检测高阻故障。此外,当系统出现电压跌落时,利用换流器的高可控性对故障电流进行限流控制［20-21］,以防止换流器发生闭锁,在此基础上快速注入信号以检测故障。注入谐波信号h(t)如式（13）所示。

式中:k为比例系数,用于改变每个信号周期；T为谐波信号h(t)的周期；|h(ω)|为信号h(t)在频率ω下的幅值；α为信号幅值的阈值；t为时间。

通常情况下,随着注入谐波信号频率的增大,其在电缆中的损耗衰减作用急剧增加［22］。对于长达几百千米的海底电缆,为了减少信号衰减,选择频率100 Hz 以下的注入信号。一方面,注入谐波幅值α应小于系统额定电流的5%,以确保注入信号不会影响系统的正常运行；另一方面,注入信号幅值α应大于系统额定电流的3%,以保证故障定位方法的灵敏度［23］。

故障定位方法流程如图6 所示。利用计算节点的谐波数据构建双节点定位方程以确定虚拟故障点,分析虚拟故障点与实际故障点之间的位置关系以构建虚拟双节点方程,从而计算出故障距离。依次选择两个不同的计算节点并重复上述步骤直到所有计算节点组合都计算完成,构建判断矩阵并记入计算结果,根据判断矩阵特征可判别故障支路并确定故障位置。

图6 故障定位方法流程图Fig.6 Flow chart of fault location method

4 仿真分析

4.1 基于虚拟故障点的主动故障定位方法

“海王星”系统拓扑结构如图7 所示。根据环型结构分解原则,需要先确定两岸基站之间最长连通路径,从岸基站47 开始建立相应的结构树,遍历全部可连通路径并比较长度后即可确定系统的最长可连通路径。基于最长连通路径对拓扑结构做相应调整,系统中存在二连环网如附录A 图A2（a）所示。根据多连环网分解方法,选择节点6 为二连环网的分解点。二连环网分解后仍存在单个环网,通过比较分支点与岸基站之间的最短距离,选择节点25 为单个环网的分解点。

图7 “海王星”系统拓扑Fig.7 Topology of NEPTUNE system

完成环网分解后,可以将连通数为2 的节点与所在分支点间电缆进行合并,并对剩余节点和分支重新编号,各电缆支路分别记为B1,B2,…,B13。连通数为1 的节点都须被选为附加量测节点,如附录A 图A2 （b）所示。

4.2 故障定位方法验证

本文利用PSCAD 进行全波傅里叶滤波,其中窗口时间为20 ms,采样频率为2 400 Hz,每工频周期采样48 个点。不同的分段间隔会影响故障定位精度和定位时间,如附录A 表A1 所示。从表中结果可知,分段间隔从10 km 减小到100 m 时,故障定位精度有明显的提升,且定位时间的增长不大。在分段间隔减小到10 m 后,故障定位精度几乎没有提升,但定位所消耗时间却大大增加。因此,在保证故障保护快速性的同时应尽可能减小分段间隔,本文所选分段间隔为10 m。

在电缆支路B9（故障1）、B6（故障2）、B13（故障3）、B1（故障4）分别设置不同过渡电阻的短路故障。故障定位误差依据式（14）计算。

式中:Er为相对误差；CL为计算所得故障距离；L为实际故障距离。

在故障1 发生且电缆支路B9被选为参考支路时,不同过渡电阻下计算电压差如附录A 图A3 所示。不同过渡电阻下最小计算电压差都位于所选参考支路上,且都小于所选参考支路的长度60 km,因此构建的所有虚拟双节点定位方程都存在有效解。

以故障1 为例,当过渡电阻为10 Ω 时,判断矩阵结果如附录A 图A4 所示。从图中结果可得,B9支路所对应行全部为有效解,所对应列全部无解,恰好符合式（8）—式（9）。且判断矩阵中其他支路特征都与式（8）—式（9）不匹配,因此,可以判断B9为故障支路。将B9支路所对应行的有效解取算术平均值,可得故障位置离计算节点8 的距离为40.121 km。不同故障场景下定位结果如表1 所示。由表中结果可得,在任何故障情况下所提方法都能准确识别故障支路,并且能够实现故障距离的准确计算,其平均故障定位误差为0.459%。

表1 不同过渡电阻下“海王星”系统故障定位结果Table 1 Fault location results of NEPTUNE system considering different transition resistances

将本文所提方法与直流配电网中的行波法［24］和暂态分析法［25］进行对比,系统参数与附加量测点保持一致,在不同故障场景下故障定位结果如表2所示。从表中结果可知,行波法和暂态分析法都存在较大的定位误差,而本文方法在不同故障场景下均可实现准确定位。由于海底分支单元中存在的齐纳二极管会使行波发生反射和折射,导致难以准确捕捉到行波波头。因此,行波法在海底供电系统中定位精度较差。同时,由于海底供电系统中存在多个海水电极,在故障时海水电极发生电化学反应会影响电极阻抗参数,导致无法准确提取线路的暂态故障特征,因此暂态分析法的定位精度也不高。本文所提方法利用故障后稳态谐波数据进行定位,不受齐纳二极管和海水电极阻抗的影响,更加适用于海底观测网供电系统且定位精度较高。

表2 不同故障定位方法的比较Table 2 Comparison of different fault location methods

在“海王星”系统分支点附近设置高阻抗短路故障,分别模拟在支路B9（故障1）和B13（故障3）上发生故障,故障定位结果如附录A 表A2 所示。在不同过渡电阻和故障距离情况下,分支点附近0.5 km到1.5 km 内的故障都能被准确定位,且平均故障定位误差为0.779%。进一步,将本文方法和常用阻抗法［26］与相位突变法［27］进行比较,系统参数和附加量测点保持一致,不同故障场景下的故障定位结果如表3 所示,表中符号“-”表示无法正常定位故障。由表可知,当故障位置离分支点较近时,阻抗法无法准确判断故障支路,导致存在较大的定位死区。这是由于在分支点发生高阻故障时,由各节点计算得到的分支点电压基本相同,阻抗法难以通过比较分支点故障附加电压准确判断故障支路。相位突变法在分支点附近过渡电阻较大时会出现对故障分支的误判,且故障位置离分支点越近,相位突变法越容易出现误判。这是因为相位突变法并没有考虑分支电流对电流相位的影响,导致难以根据相位特征准确判别分支点附近的高阻故障。而所提方法提出使用虚拟故障点对线路进行二次电压差搜索,可以消除分支电流的影响,且充分利用了所有量测节点的故障信息,在不同故障情况下都能准确识别故障分支,且平均故障定位精度为0.36%。综上可得,所提方法能够准确定位多端环型供电系统中分支点附近的高阻抗短路故障,有效减小了分支点附近的死区范围。

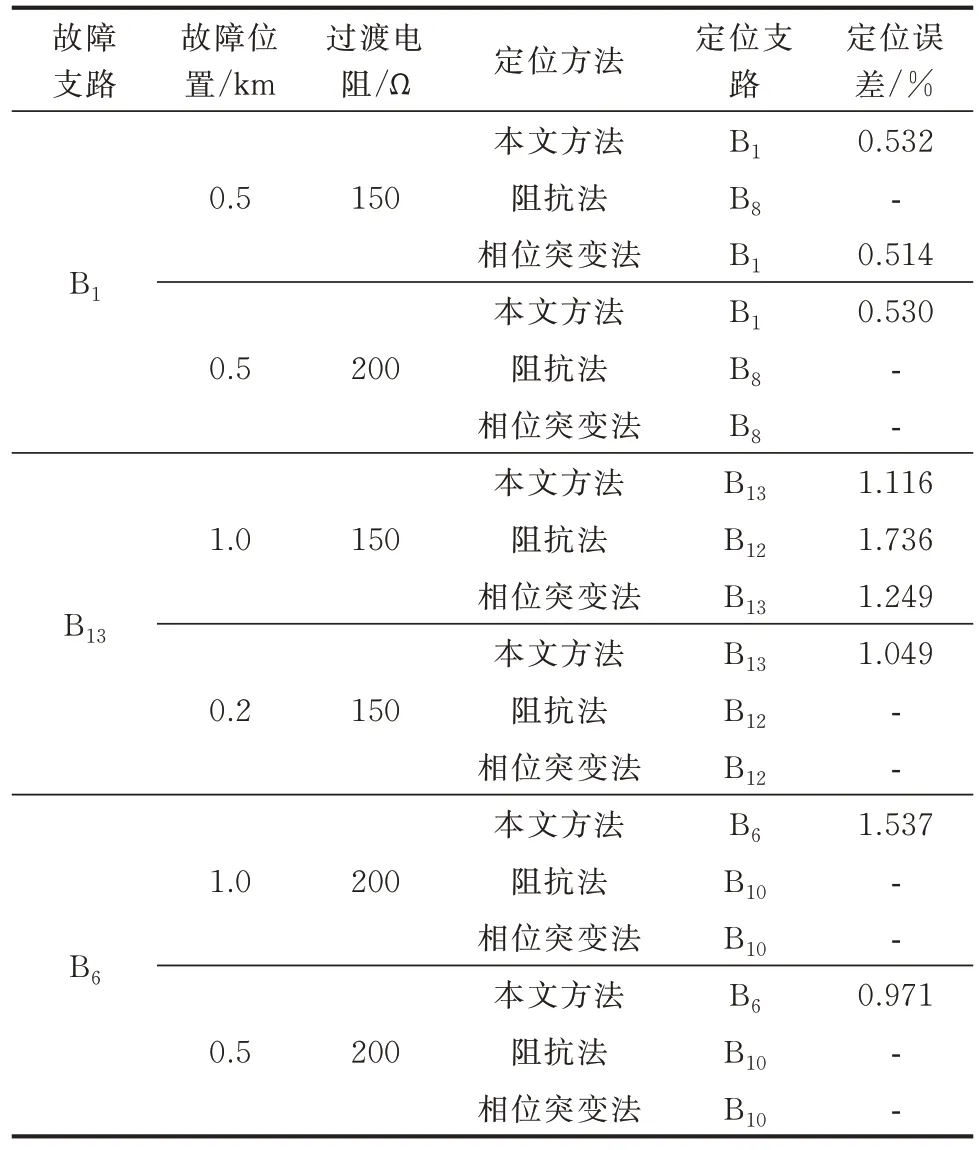
表3 分支点附近故障时不同故障定位方法的比较Table 3 Comparison of different fault location methods when faults are close to branch points

5 结语

有限量测数据给多端环型海底观测网供电系统故障定位带来了严重挑战,本文提出了一种附加量测节点的故障主动定位方法,选择不同电缆支路构建双节点定位方程以确定虚拟故障点,通过分析虚拟故障点与实际故障点相对位置关系以计算故障距离,构建判断矩阵并分析其特征以实现故障定位。建立了“海王星”系统模型,并在不同故障场景下对所提方法进行验证,故障定位平均误差小于0.6%,针对分支点附近的高阻故障,平均定位误差小于1.0%。本文方法有效提高了多端环型海底观测网直流供电系统的可靠性与安全性。下一步将研究多点高阻故障的准确定位方法,拓展本文成果的应用范围。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。