基于能路的综合能源系统安全域稳态建模与求解

2023-10-21宋晨辉李宗哲李瑾一李承晋

电力系统自动化 2023年19期

肖峻，宋晨辉，焦衡，李宗哲，李瑾一，李承晋

（1.智能电网教育部重点实验室（天津大学）,天津市 300072；2.长沙理工大学电气与信息工程学院,湖南省长沙市 410114；3.北京电力经济技术研究院有限公司,北京市 100055）

0 引言

以电力和天然气等异质能源系统为核心的综合能源系统（integrated energy system,IES）通过多能耦合,实现了异质能源协同互补与能量梯级利用［1］,是实现“双碳”目标的关键物理载体,但多能耦合也增加了系统运行的安全风险［2］。

安全性是系统运行的基础。单一能源系统已形成较成熟的安全分析方法［3-4］。对于IES,不仅需保障单一能源系统运行安全,还需注意系统交互带来的安全问题,应站在综合视角上对IES 安全性进行统一分析［2］。但IES 安全性的研究仍处于起步阶段,目前,主要围绕逐点法展开［2,5］,存在以下不足［6］:1）每次校验安全性时,都需预先进行多能流计算,计算耗时难以满足安全分析的在线需求；2）无法获取IES 完整运行范围与安全边界,无法给出工作点安全性的整体测度、可调裕度等调度员和市场参与者关注的信息。

与逐点法相比,安全域方法具有以下优势［3］:1）将能流计算等过程转移至离线预先完成,大大提升了在线安全分析的效率；2）通过计算工作点到安全边界距离,能得到系统安全裕度；3）能获取系统的全局安全信息,便于实现态势感知和主动预防控制。因此,研究人员借鉴电力系统安全域（security region of electric power system,EPS-SR）,对综合能源系统安全域（security region of integrated energy system,IES-SR）展开了研究［6-12］。文献［7］最早提出了IES-SR 的概念与模型。后续研究［6,8-12］在文献［7］基础上进行了扩展:文献［8］考虑风电随机性,提出了基于凸包的鲁棒IES-SR；文献［6］考虑了N-1安全性；文献［9］对IES 中的天然气网安全域进行研究；文献［10］在IES-SR 建模时,全面考虑了异质能源的多能流与压力约束；文献［11］研究了IES-SR的拓扑特征和基于动力学的安全域求解方法；文献［11］研究了IES-SR 的拓扑特征和基于动力学的安全域求解方法；文献［12］研究了耦合性对IES-SR的影响机理。IES-SR 弥补了逐点法的不足,但其研究仍存在以下问题:

1）已有的IES-SR 稳态模型均基于异质能源系统固有的能量流动方程［3-4］,这些方程多为非线性关系,数学形式与求解方法各异［13］,增加了IES-SR 尤其是高维IES-SR 的求解难度。虽然安全域在离线计算时并没有明确的时间要求,但对于大型IES-SR的完整高维结果计算,若不考虑计算效率,将耗费大量的计算时间与资源,导致其离线计算时难以得到计算结果。

2）计及网络动态特性的IES-SR 尚无研究。相较电力传输,天然气流动的时间常数为分钟、小时级,在这一时间尺度上的动态特性仍较为显著,若采用时空相关的偏微分方程描述,IES-SR 的建模与求解过程将变得非常复杂。

上述问题的成因在于异质能源系统缺乏兼顾精确性与复杂度的标准化模型。异质能源统一建模方法［13-20］为该问题提供了解决思路。该方法的思想在于考虑异质能源传输特性的差异性与网络特征的相似性,在一定条件下建立统一形式的数学模型［16］,通常为代数方程形式的标准化网络方程,而在此之前,天然气管网尚未采用过类似的网络方程进行分析。此外,异质能源统一建模通过等值参数进行不同系统间的信息交互,避免了直接提供管网实际参数,能更好地保护数据隐私,降低实际中的信息壁垒。统一建模方法主要包括广义电路理论［15-16］与统一能路理论［13,17-20］,本文主要基于能路理论［13,17-20］。能路研究已涉及建模方法［17-18］、多能流计算［13］、状态估计［19］、优化调度［20］等,但尚未见到在IES-SR 方面应用的报道。

本文是系列论文的第2 篇,首篇基于能路的天然气系统安全域（security region of natural gas system,NGS-SR）主要针对单一能源系统,本文首次建立了多能源耦合系统的能路安全域模型,在稳态层面上实现了电-气IES-SR 的数学形式统一。

1 IES-SR 的基础概念

1.1 工作点定义

电力系统采用工作点［3］描述安全性。参考电力系统定义IES 工作点:能描述系统运行状态安全性的最小变量集合。IES 运营时,负荷通常是需求主体,而电源、气源等通常是服务主体,服务主体应按照协议帮助系统满足安全运行需求［21］。因此,IES的工作点变量选取系统的负荷:

式中:W为工作点；Sl,ei为电力负荷节点i的功率；Gl,gj为天然气负荷节点j的流量；i=1,2,…,m,m为电力负荷节点数；j=1,2,…,n,n为天然气负荷节点数。附录A 给出了本文涉及的缩写名词与数学符号的详细说明。

区别于单一能源系统,IES 通过耦合单元建立了异质能源系统的联络关系。本文选用图1 所示的两类典型耦合单元:天然气压缩机作为电力负荷,由电力系统提供驱动功率；燃气发电机（GT）作为天然气负荷,由天然气系统提供输入流量。

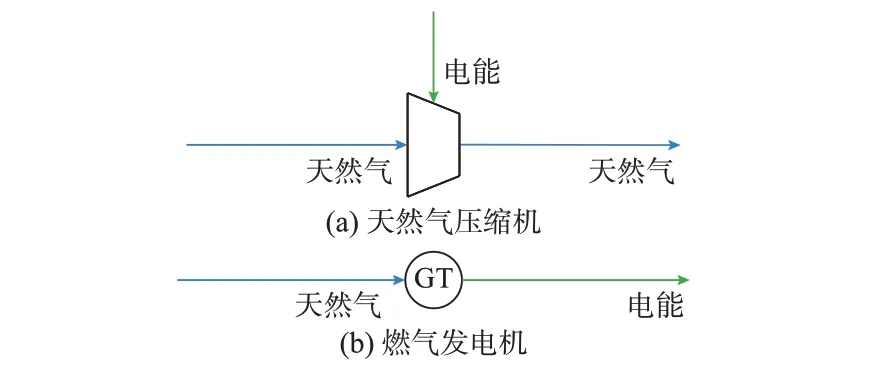
图1 典型耦合单元示意图Fig.1 Schematic diagram of typical coupling units

在区分耦合单元负荷与各异质能源系统固有负荷时,本文将工作点表示为式（2）形式。

式中:Sl,ci为驱动压缩机i所需的电功率；Gl,GTj为燃气发电机j输入的天然气流量。

1.2 安全性定义

类比电力系统［3］和天然气系统［4］,将IES 安全性定义为:对于某工作点,其所有状态量是否满足运行约束,若满足则运行安全,该点是安全工作点,记为Ws,若不满足则该点不安全。

IES 的临界安全性定义为:对于一个安全工作点,是否至少存在一个负荷节点,在其功率/流量增加或减少后,形成的新工作点将不安全。若存在,则系统临界安全,原工作点是临界安全工作点,简称临界点,记为Wb。规定功率/流量增加导致的临界安全性为正临界性,减少导致的临界安全性为负临界性。

1.3 安全域定义

IES-SR 定义为:IES 运行时,所有安全工作点构成的集合,记为ΩIES。IES-SR 在状态空间中为封闭区域,由EPS-SR 和NGS-SR 构成。

IES 安全边界定义为:IES-SR 中所有临界点构成的集合,记为∂IES。安全边界分为上边界和下边界:上边界由具有正临界性的工作点构成；下边界由具有负临界性的工作点构成。

本文沿用供电能力［22］（total supply capability,TSC）和输气能力［23］（gas transmission capability,GTC）来描述IES 安全运行时的最大供能能力,TSC 点和GTC 点分别对应IES 供电量和输气量最大时的运行状态,是IES-SR 中的高效工作点。

2 基于能路的IES-SR 建模

2.1 能路模型

异质能源统一建模时,采用能路分析能量流动过程,如电能采用电路、天然气采用气路［13,17,23］、热能采用水路和热路［13,18］。利用能路模型,可以建立具有相同数学形式的网络方程,实现异质能源系统能量流动平衡关系的统一描述。

2.1.1 电力系统的电路和网络方程

电力系统一般采用π 形电路［24］对支路进行等值,对应的网络方程如下:

式中:Ye为节点导纳矩阵；Un和In分别为节点电压和注入电流构成的向量。

引入电力系统网络方程,目的是建立形式统一的能路安全域模型,使得网络结构的能量系统都可由其扩展。此外,还具有如下优势:1）网络方程是电力系统的基本模型,是稳态、暂态分析的基础,网络方程建模具备通用性,便于扩展；2）电力系统的许多场景中,网络方程更易于直接应用,如采用分布系数法分析支路开断影响；3）符合安全域研究习惯,基于网络方程的EPS-SR 建模很常见［3］,如热稳定安全域等。网络方程在潮流分析可采用交流或直流模型［24］。

2.1.2 天然气系统的气路和网络方程

在能路模型中,天然气系统采用图2 所示的π形气路［17,23］对管道进行等值,如图2 所示。图中:Zb、kb和Y1、Y2分别为π 形气路的支路阻抗、受控气压源和对地导纳,l为管长。

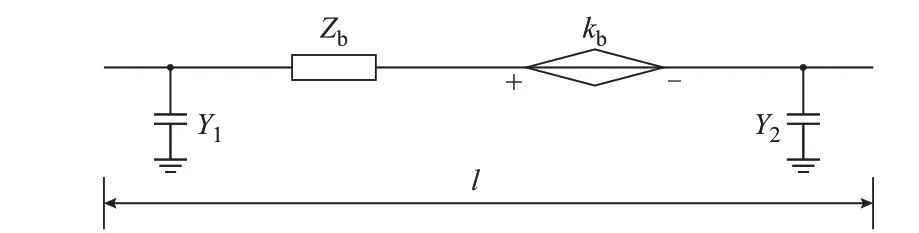
图2 天然气管道的π 形气路Fig.2 π-type gaseous circuit of natural gas pipeline

π 形气路参数在稳态［23］时的计算公式如下:

式中:λ、vb、s、d和θ分别为管道的摩擦系数、流速基值、横截面积、内径和倾角；g为重力加速度；R和T分别为天然气气体常数和温度。

文献［23］推导了气路对应的稳态网络方程,与电力系统网络方程的数学形式相同,即

式中:pn和Gn分别为节点天然气气压、流量构成的向量；Yg为天然气系统的广义节点导纳矩阵,计算公式如下

式中:Ag、Ag+和Ag-分别为节点-支路关联矩阵、节点-流出支路关联矩阵和节点-流入支路关联矩阵［23］；K为压缩机压比方阵［23］；yb和kb分别为支路导纳和受控气压源构成的对角矩阵,矩阵元素为π 形气路的对应参数值。

2.2 安全域模型

2.2.1 安全域

利用能路模型,IES-SR 的稳态模型为式（12）所示形式。

式中:Ws为安全工作点,需满足平衡约束h（Ws）和安全约束g（Ws）,即式s.t.（1）至（3）所示的3 类约束,s.t.（1）至（3）的具体含义如下。

1）s.t.（1）为电力系统约束,依次为:电力网络方程、节点电压上下限,节点注入（发电机、负荷）有功和无功功率上下限,支路功率上限。其中,Umaxn、Uminn分别为节点电压上、下限构成的向量,Pn、Qn分别为节点注入有功和无功功率构成的向量,Pmaxn、Pminn和Qmaxn、Qminn分别为节点注入有功和无功功率的上、下限构成的向量,Sb为支路视在功率构成的向量,Smaxb为支路容量构成的向量。

2）s.t.（2）为天然气系统约束,依次为:天然气网络方程、节点气压上下限、节点注入流量上下限、管道流量上限。其中,Gmaxn、Gminn和pmaxn、pminn分别为节点气压和注入流量上、下限构成的列向量,Gb为管道流量构成的向量,Gmaxb为管道容量构成的向量。

3）s.t.（3）为耦合单元约束,描述了异质能源网络间的能量流动关系。约束依次为:压缩机驱动耗电方程［25］、燃气发电机耗气方程［25］。其中,Sl,c为驱动压缩机所需的电功率,Gl,GT为燃气发电机输入的天然气流量,p0、T0分别为标准大气压强和标准温度,Z、κ和VGH分别为天然气的压缩因子、绝热常数和总热值,η、K和Gc分别为压缩机的效率、压比值和流经流量,aGT、bGT、cGT、dGT和eGT为燃气发电机热耗系数,PGT为燃气发电机输出的有功功率,PminGT为PGT的下限值。

上述IES-SR 模型中,若只计及约束s.t.（1）,则为传统的EPS-SR,若只计及约束s.t.（2）,则为基于能路的NGS-SR［23］。可见,采用能路后,单一异质能源系统的安全域模型非常易于向IES-SR 模型扩展,且彼此间的状态量具有对应关系,其数学形式是相互统一的。

2.2.2 安全边界

IES-SR 安全边界模型如式（13）所示。含义如下:xi为工作点元素,Wb∈ΩIES表示工作点Wb位于域内,是安全工作点,Wb任一元素xi增加ε*后形成新工作点W*。若∀ε*≠0,∃i=1,2,…,n,使得W*∉ΩIES,则Wb是一个边界点,全部Wb构成安全边界。若ε*>0,则Wb具有正临界性,位于上边界；若ε*<0,则Wb位于下边界。

2.2.3 供能能力

IES 供能能力包括TSC 和GTC,模型如下:

式中:STSC为TSC 点下的IES 总供电量；GGTC为GTC 点下的IES 总输气量。

3 安全域求解

3.1 求解难点与解决思路

安全域的维度取决于工作点的维数［26-27］。由于IES 的工作点维数通常较高,故IES-SR 通常为高维状态空间中的超多面体。这给IES-SR 的求解带来了以下困难:

难点1:难以求解高维IES-SR 完整的安全边界表达式。这是由于在高维空间中,超多面体形式的IES-SR 无法直接观测,使得无法观测到安全边界发生大幅曲率变化的分界处,进而难以找到对安全边界进行分段拟合时的分段点。

难点2:求解效率低。由于IES-SR 在边界点求解时,需要通过多能流计算［5］校验工作点的安全性。当安全域维度增加时,待校验的工作点数量将呈指数增长,若在多能流计算时,仍基于异质能源网固有的能量流动方程对工作点进行安全性校验,将耗时巨大。

本文针对上述难点的解决思路如下:

1）针对难点1,本文提出一种适用于高维状态空间安全域的安全边界表达式拟合方法,通过计算边界点到超平面的距离,实现分段点的自动求解。该拟合方法无须通过观测,即可得到安全边界发生曲率变化的分界。

2）针对难点2,本文在多能流计算时,利用网络方程代替异质能源网固有的能量流动方程,一定程度上避免了非线性方程的迭代求解过程,节省了计算时间。

3.2 求解方法的具体过程

基于上述方法,可得到高维IES-SR 的完整安全域结果,包括安全边界点与拟合所得安全边界表达式。具体过程如下:首先,进行网络方程求解,获得工作点的完整状态量,这是边界点求解的基础；其次,进行边界点求解,目的是找到满足临界安全性的工作点；最后,通过安全边界拟合,得到安全边界表达式。

3.2.1 网络方程求解

网络方程求解,即异质能源系统的多能流计算是IES 工作点安全校验的基础。对于电力系统网络方程,现有方法［7］常采用雅可比矩阵方法,为方便对比,本文也采用该方法。以下介绍天然气系统网络方程求解与耦合单元约束处理过程。

1）天然气系统网络方程求解

首先,类比电力系统,天然气系统节点可分为定压力节点和定流量节点,如表1 所示。

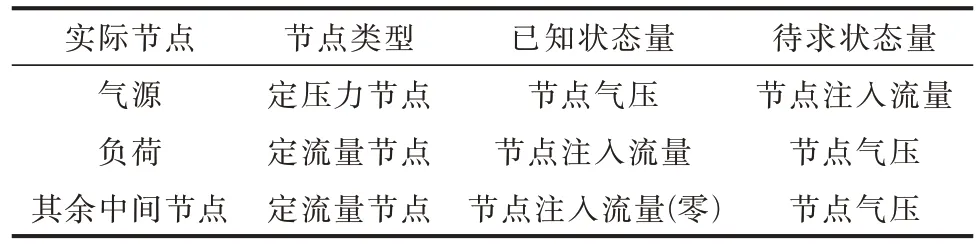
表1 天然气系统网络方程求解时的节点分类Table 1 Node classification during solving network equations of natural gas system

接着,按节点类型,重排式（10）的网络方程,得到:

式中:pp和Gp分别为定压力节点的节点气压和注入流量构成的向量；pg和Gg分别为定流量节点的节点气压和注入流量构成的向量；Yg,pp、Yg,pg、Yg,gp和Yg,gg分别为Yg重排后的对应分块。

最后,由式（16）可解得Gp和pg如下:

2）耦合单元约束处理

首先,基于能量流动关系,将异质能源系统中的耦合单元所在节点分类,如表2 所示。

表2 耦合单元的节点分类Table 2 Node classification of coupling units

接着,根据耦合单元在天然气系统中的节点分类,求解天然气网络方程,得到天然气系统的完整状态量。

最后,根据式（14）中的耦合单元约束方程,计算耦合单元在电力系统网络方程求解时所需状态量,从而实现异质能源系统间能量的参数传递。

3.2.2 边界点求解

文献［23］提出了基于气路的NGS-SR 求解方法,采用二分法求解边界点:通过对工作点迭代修正,将其修正至边界点。本文借鉴该方法,用于求解IES-SR 边界点。求解时,选定工作点的任一元素进行修正,对其余元素等间隔采样；同时,为方便后续的安全边界拟合,需保证求得的边界点个数不小于安全域维数。

3.2.3 安全边界拟合

IES-SR 是N维状态空间中的封闭区域,当N>3 时,常通过二维/三维观测［6-7］,得到域的降维视图［6-7］及对应的边界表达式,但降维后仅能反映IESSR 局部信息。边界点是N维的,反映了IES-SR 全局信息,但边界点在状态空间中是离散的,相对表达式不易使用。为此,本文提出一种拟合方法,能求解高维IES-SR 的安全边界表达式。

类比电力系统［3］,用一组超平面刻画IES-SR 的安全边界,采用分段线性化方法对超平面进行拟合。拟合难点在于:高维空间中难以找到超平面间合适的分段点。这是因为在高维空间中,难以直接观测到边界发生大幅曲率变化的分界。本文通过计算边界点到超平面的距离,实现分段点的自动求解。具体拟合步骤如下:

1）设定距离误差阈值Dmax。Dmax表示拟合时,全部边界点到拟合超平面距离的上限,代表了超平面的拟合精度,是分段拟合的结束条件。

2）构建初始超平面。首先,为提升拟合速度,应在保证精度的前提下减少拟合次数。因此,对于首次拟合的初始超平面,选取覆盖域范围尽可能大的N个线性无关的边界点进行拟合。初始超平面方程如下:

式中:H0为初始超平面方程；a0i、b0为H0的拟合系数,拟合系数可由拟合时选取的边界点计算得到；βi为H0的变量,与工作点元素相对应；N为IES-SR 的维度。

接着,计算各边界点到H0的距离。对于边界点Wb=[x1,…,xi,…,xN],Wb到H0的距离DWb→H0为:

3）分段线性拟合。第k次分段拟合时的步骤如下。

首先,对于选取的边界点,若满足线性无关条件,则按分组拟合成式（19）所示形式的超平面,共得到M个超平面方程。

接着,按式（20）计算边界点Wb到各个超平面的距离,取其中的最小值:

DWb→H k=min(DWb→Hjk)j=1,2,…,M（21）

需要指出,对于N维安全域,由于其每次超平面拟合时都选用了N个线性无关的边界点,从而保证了超平面拟合结果的唯一性。

4 算例分析

4.1 测试算例原始数据

以图3 所示的算例1 作为测试算例进行验证,系统由5 节点天然气系统［23］和3 节点电力系统［25］组成。图中:驱动压缩机cg所需电功率由电力节点Ne3提供,燃气发电机GT 所需天然气功率由天然气节点Ng2提供（图中用红色虚线表示）。具体参数如表3—表6 所示。

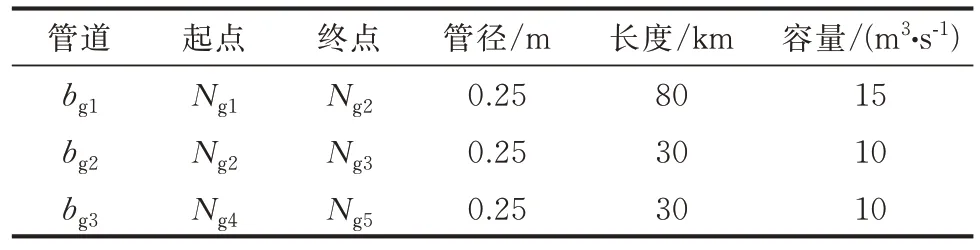
表3 算例1 的天然气系统管道参数Table 3 Pipe parameters of natural gas system in case 1

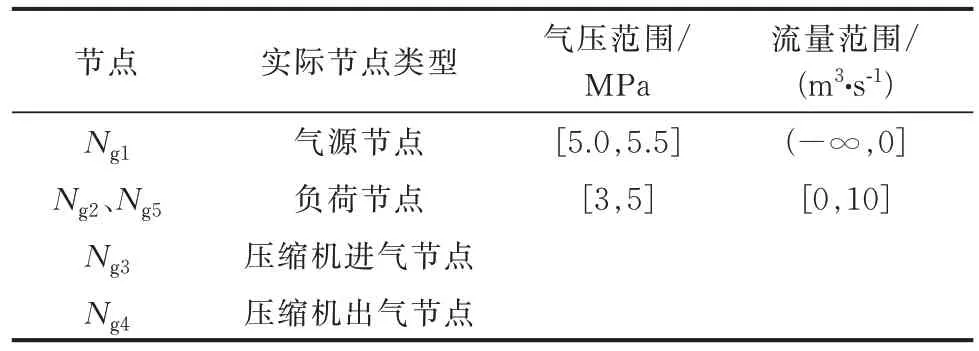
表4 算例1 的天然气系统节点参数Table 4 Node parameters of natural gas system in case 1

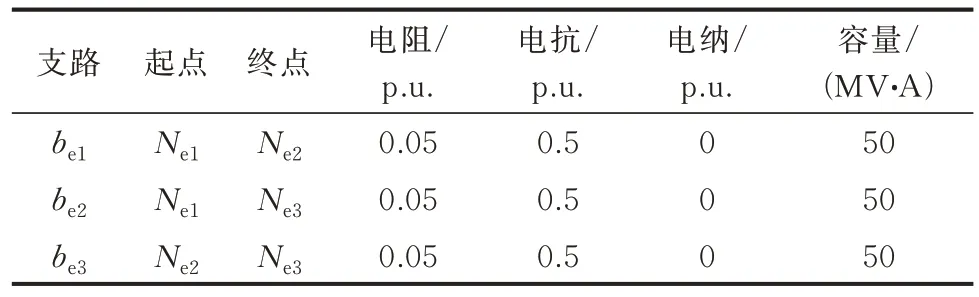
表5 算例1 的电力系统支路参数Table 5 Branch parameters of power system in case 1

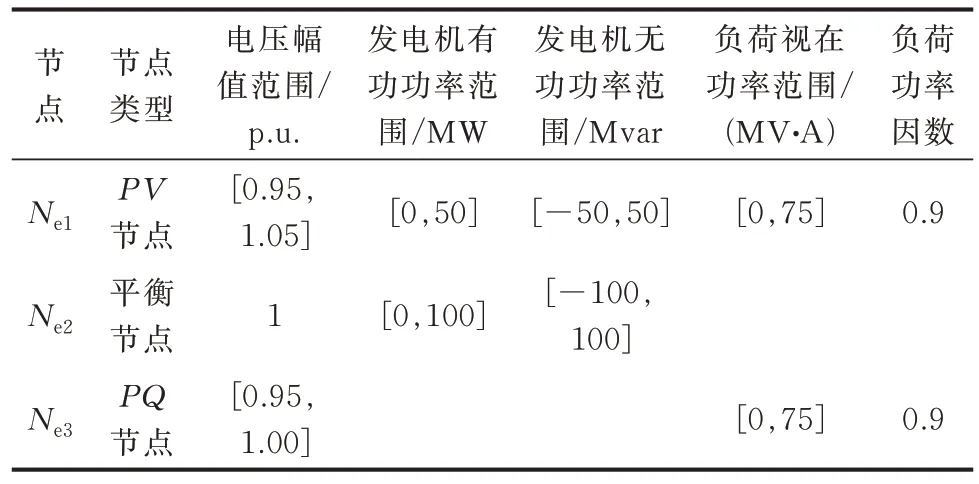
表6 算例1 的电力系统节点参数Table 6 Node parameters of power system in case 1

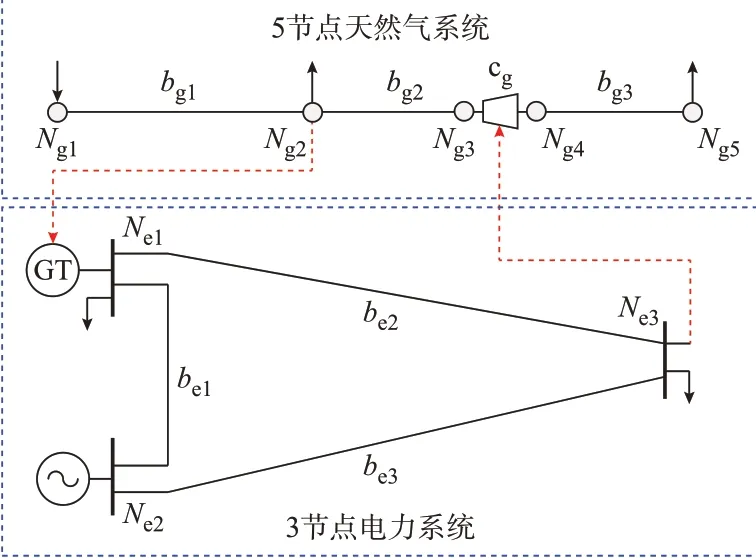
图3 算例1 系统结构Fig.3 System structure of case 1

4.2 测试算例安全域求解与观测

IES-SR 的求解结果包括边界点与安全边界表达式,观测结果为局部降维视图。实验环境如下:处理器为2.5 GHz Intel Core i5-2450M CPU,内存4 GB,仿真平台为IntelliJ IDEA。

4.2.1 安全域的完整求解结果

求解参数如下:在状态空间中对Sl,e1、Sl,e3、Sl,c、Gl,g2、Gl,GT等间隔采样；修正Gl,g5,修正时收敛精度取0.01。共求得上边界点25 731 个,如表7 所示；下边界点12 115 个,如表8 所示。

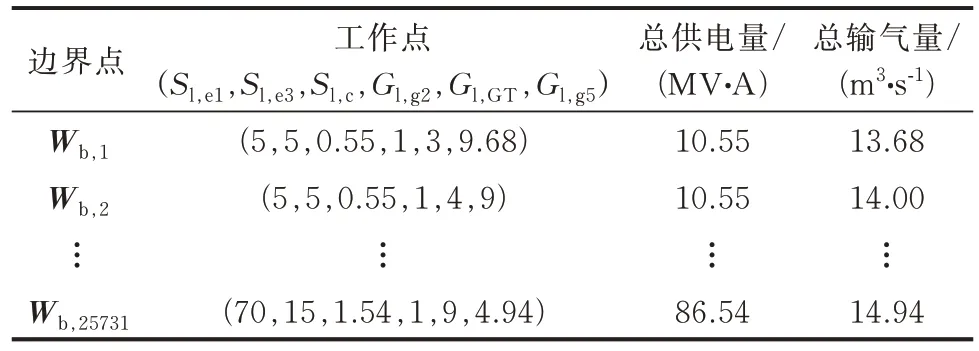
表7 算例1 的IES-SR 上边界点Table 7 Upper boundary points in IES-SR in case 1

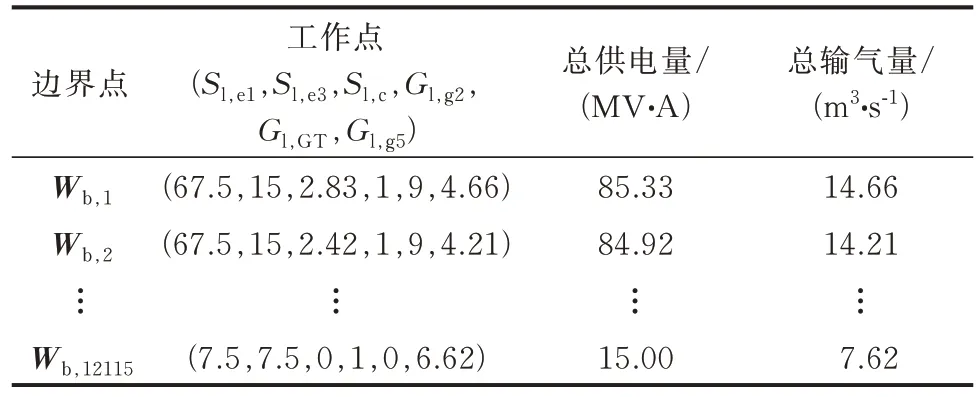
表8 算例1 的IES-SR 下边界点Table 8 Lower boundary points in IES-SR in case 1

计算边界点的总供电量和总输气量,求得算例1 的TSC 和GTC 分别为97.83 MV∙A、14.94 m3/s,表9 展示了对应的TSC 点和GTC 点。这些点是IES-SR 中的高效工作点,分别代表了IES 供电量和输气量最大时的运行状态。

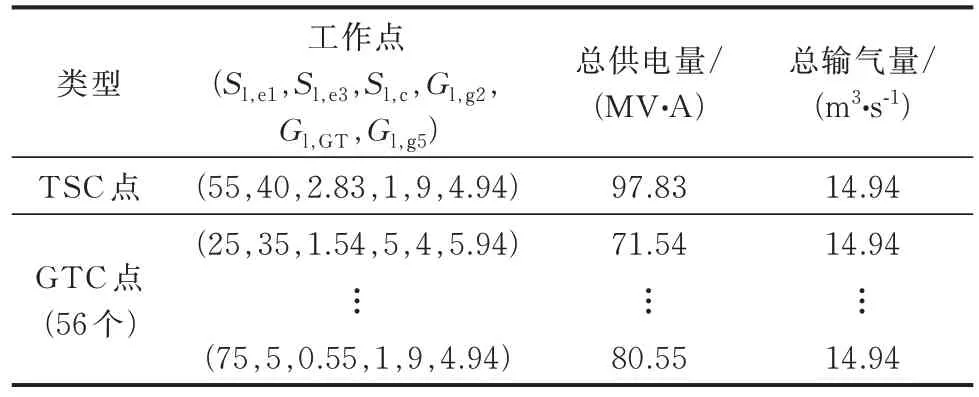
表9 算例1 的TSC 点与GTC 点Table 9 TSC point and GTC points in case 1

利用边界点拟合安全边界,设定距离误差阈值为0.1,可得到41 个上边界超平面、61 个下边界超平面,如表10 所示。

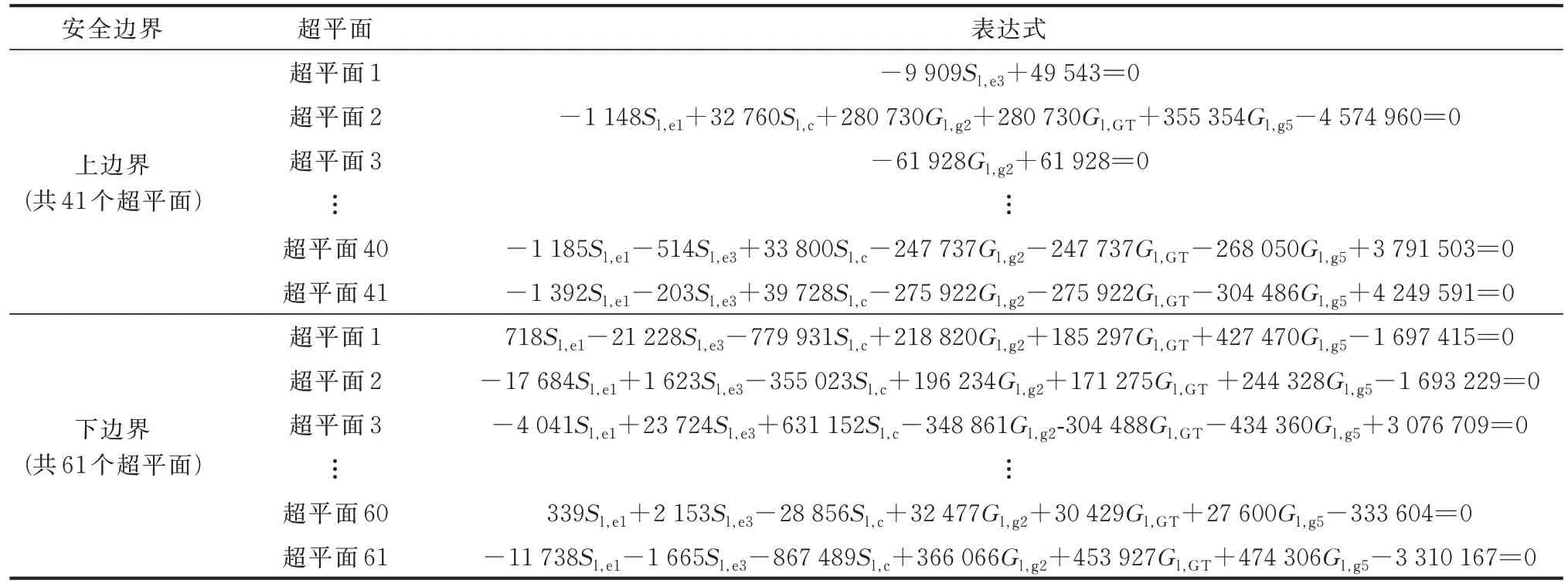
表10 算例1 的安全边界表达式Table 10 Expression of security boundary in case 1

4.2.2 安全域的局部观测结果

观测IES-SR 的局部二维视图。同时,为观测TSC 点、GTC 点与域的几何关系,本文基于TSC 点和GTC 点下的负荷分布进行观测。

图4 基于TSC 点（55,40,2.83,1,9,4.94）,展示了Ne1、Ne3为观测节点时的结果。由于观测节点为电力节点,该视图主要可视化了IES-SR 中EPS-SR的部分结果。可以看出,该部分域由上边界和状态空间边界围成,TSC 点位于上边界。

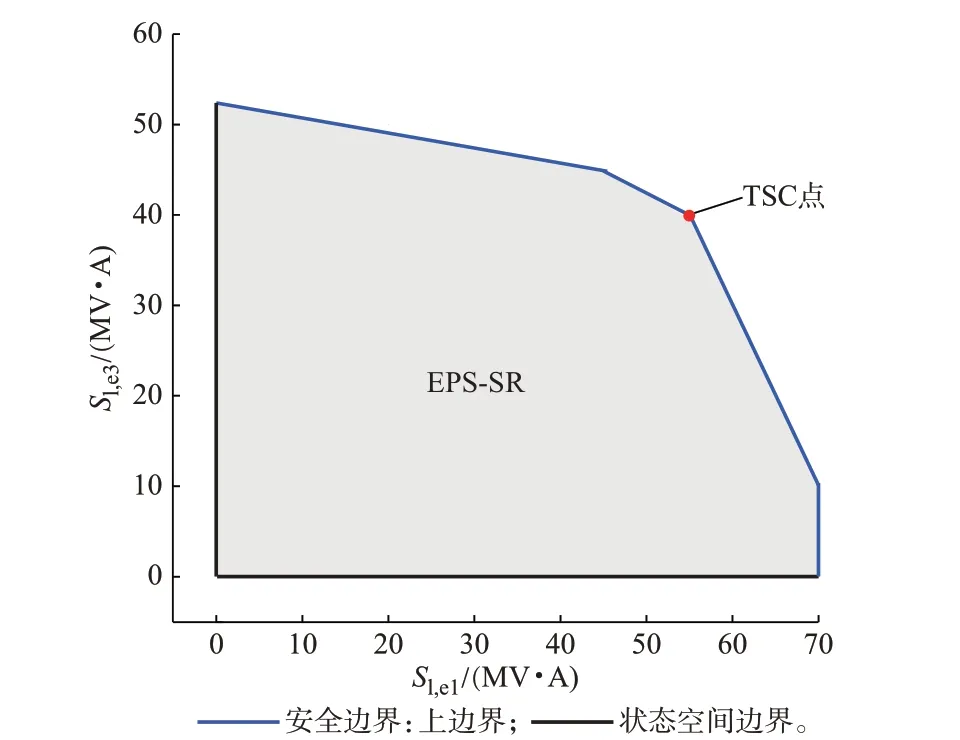
图4 算例1 的IES-SR 局部观测视图（观测节点：Ne1、Ne3）Fig.4 Partial observation figure of IES-SR in case 1(observation nodes: Ne1, Ne3)

图5 基于GTC 点（25,35,1.54,5,4,5.94）,展示了Ng2、Ng5为观测节点时的结果。由于观测节点为天然气节点,该视图主要可视化了IES-SR 中NGSSR 的部分结果。可以看出,该部分域由上边界、下边界和状态空间边界围成,GTC 点同样位于上边界。

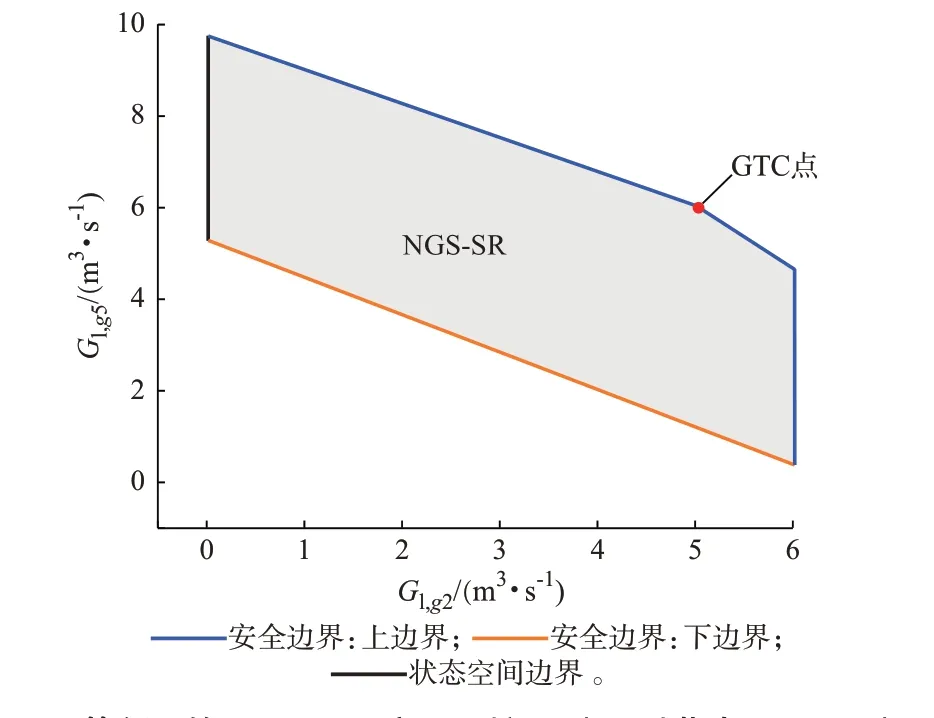
图5 算例1 的IES-SR 局部观测视图（观测节点：Ng2、Ng5）Fig.5 Partial observation figure of IES-SR in case 1(observation nodes: Ng2, Ng5)

需要说明,本文观测到的IES-SR 均为凸集,与主流研究结果［6-10］一致。安全域是凸集的原因是本文选取了负荷注入功率作为工作点元素。

4.3 与现有方法对比

首先,针对3.1 节IES-SR 求解难点1,现有方法尚未解决。现有文献［7,10］仅针对二维、三维情况,未得到高维安全边界的完整解析式。本文首次得到了高维IES-SR 安全边界的完整边界解析式,具有如下优势:

1）完整的安全边界表达式包含IES-SR 的全局信息,刻画了高维状态空间中IES 安全运行的完整边界；而现有方法只能得到高维空间中IES-SR 的降维结果［7］,该降维结果仅包含IES-SR 的局部信息,只刻画了IES 安全运行的部分边界。

2）利用安全边界表达式,能分析状态空间中任意工作点的安全性,并能计算出工作点在状态空间中所有方向上的安全裕度［28］；而现有方法仅能对位于降维断面上的工作点进行安全分析,且仅能计算断面维度方向上的安全裕度［29］。

其次,关于3.1 节IES-SR 求解难点2,对比现有方法和本文方法对IES-SR 边界点的求解精度和耗时。文献［7］最早提出了IES-SR 的概念,采用异质能源系统固有的能量流动方程建模；后续研究［6,8-12］在文献［7］基础上进行了扩展,但基本模型与文献［7］无本质区别。因此,本文选取文献［7］方法进行对比。对比结果如表11 所示。

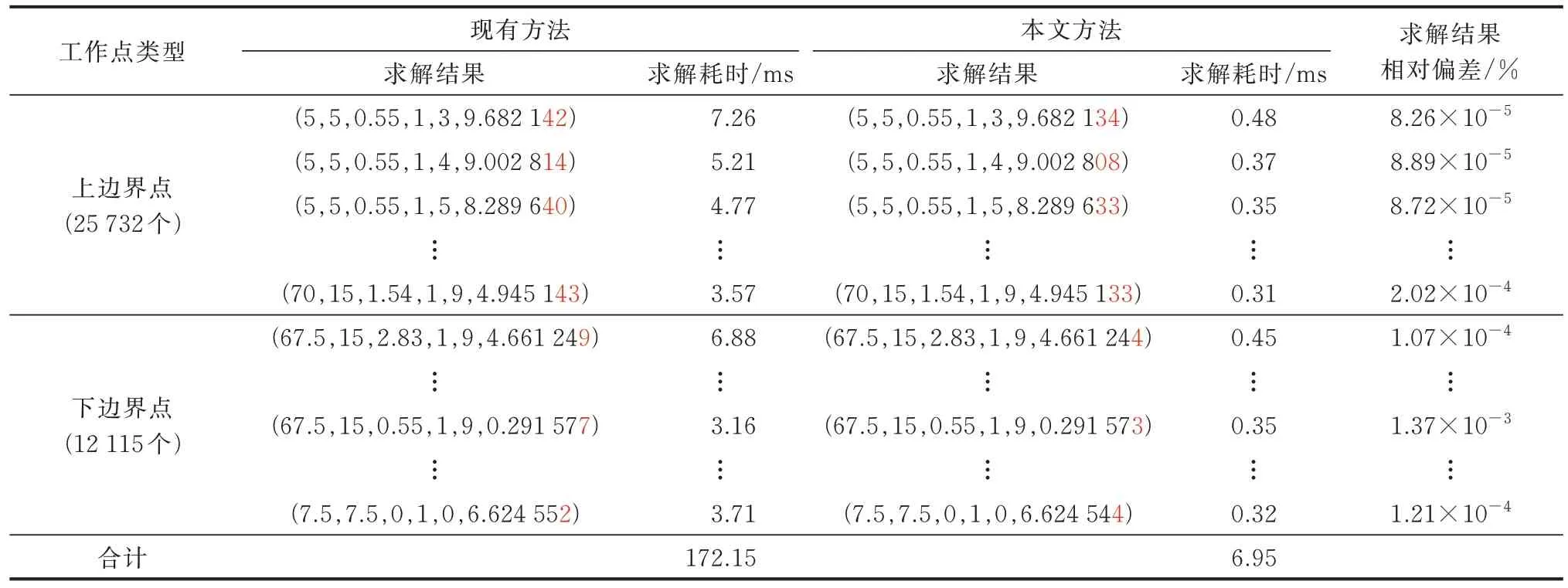
表11 本文方法与现有方法求解边界点精度与耗时对比Table 11 Comparison of precision and calculation time between method in this paper and existing method for solving boundary points

由表11 可以看出:1）两方法求得边界点数相同,边界点一一对应；2）两方法求得边界点偏差很小,最大相对偏差仅为0.001 37%。该偏差并不会影响到求解结果的保守性,原因是该偏差仅会影响到边界点在0.000 01 后的精度,远小于边界点修正时设置的收敛精度0.01。

偏差很小的原因如下:现有方法采用异质能源系统固有的能量流动方程建模,更为精确。本文将异质能源系统统一建模时,引入了误差。误差主要由于气路引入了管道流速基值:若基值等于实际天然气流速,则本文网络方程与管道压降方程等价,理论上将没有误差。合理确定基值可有效减小误差［13］。本文基值确定方法及算例中的基值确定过程详见附录B。

由表11 还可以看出,本文求解边界点的效率大幅提高:现有方法求解全部边界点耗时172.15 s,本文方法总耗时6.95 s,效率提升24.77 倍。需要指出,效率提升的原因在于线性化,具体如下:进行异质能源统一建模时,通过利用网络方程代替异质能源网固有的能量流动方程,线性化了流动过程的动量守恒方程［17］,避免了多能流计算时管道压降方程求解的迭代过程,节省了计算时间。

需要说明,由于本文方法和现有方法求得的边界点偏差很小,利用两组边界点拟合得到的安全边界表达式相同,均为表10 结果。该结果进一步验证了本文方法的正确性。

4.4 实际算例验证

4.4.1 实际算例原始数据

以附录C 图C1 所示的23 节点系统作为算例2,进行实际算例验证。算例2 由比利时东南地区9 节点天然气系统［23］和IEEE 14 节点电力系统组成。图中:驱动压缩机cg1～cg3所需的电功率由电力系统节点Ne13、Ne5、Ne4提供,燃气发电机GT1、GT2所需的天然气功率由天然气系统节点Ng5、Ng8提供。具体参数设置详见附录C 表C1 至表C5。

4.4.2 实际算例安全域求解与观测

边界点求解参数如下:在工作点所有元素中,选取Gl,g9修正,修正时收敛精度取0.1；对其余元素等间隔采样。共求得IES-SR 上边界点10 513 152 个,下边界点4 725 166 个,详见附录D 表D1。由表D1可以看出,较现有方法［7］,本文求得边界点的最大偏差为0.026%。计算总耗时由136.58 h 降至2.92 h,效率提升46.77 倍。需要指出,实际应用可离线预先计算安全边界,在线分析只计算安全距离,从而实现在线安全分析［3,22］。这样,耗时可由136.58 h 降至2.92 h,大大提升了离线计算的可行性与便捷性。

利用边界点拟合安全边界,设定距离误差阈值为0.5,拟合结果如附录D 表D2 所示。附录E 进一步展示了算例2 的局部降维观测视图。