Intelligent Electric Vehicle Charging Scheduling in Transportation-Energy Nexus With Distributional Reinforcement Learning

Tao Chen and Ciwei Gao

Dear Editor,

This letter is concerned with electric vehicle (EV) charging scheduling problem in transportation-energy nexus using an intelligent decision-making strategy with probabilistic self-adaptability features.In order to accommodate the coupling effects of stochastic EV driving behavior on transport network and distribution network, a risk-captured distributional reinforcement learning solution is presented by using explicit probabilistic information for action and reward function in Markov decision process (MDP) model, where the Bellman equation is extended to a more generalized version.Scheduling EV charging in a transportation-energy nexus, according to both transport and distribution network conditions, is an important topic in recent studies to improve the driving and charging energy efficiency, especially considering the high penetration rate of EV nowadays and even more extremely higher one in the future [1].In order to accommodate the coupling effects of stochastic EV driving behavior and battery state-of-charge (SoC) on transport and distribution network, various methods have been developed for designing the smart charging scheduling strategy with consideration of electricity price, renewable energy adoption, road conditions and many others.

However, it can be pointed out that most of existing works are dependent heavily on the optimization-based solutions with assumption of convex characteristics and various pre-defined forecasting information in a deterministic manner.In practices, the transportation-energy nexus is close to a complex system without holding such good model characteristics and well-structured given input parameters for highly stochastic driving and charging behaviors.Thus, it is desirable to address EV charging scheduling problem in transportation-energy nexus environment using an distributional reinforcement learning-based strategy with probabilistic and self-adaptability features.Many EV and ordinary vehicle navigation and routing applications using deep reinforcement learning (DRL) framework are briefed and summarized in [2].Less works study the joint transport routing and energy charging problems due to the resultant complex coupled constraints of congestion management, traffic flow overlap,energy allocation and many other issues that are not incurred in separated system [3].A few works tried DRL framework to solve EV charging and navigation problems at the same time in the coordinated smart grid and intelligent transportation system [4], [5].However, most of these works just exploit conventional DRL algorithms(e.g., soft actor-critic (SAC), deep deterministic policy gradient(DDPG), deep Q-network (DQN)) that are heavily dependent on deterministic reward value feedback and hard to capture the joint uncertain and distributional probability information, especially causal risks, in the coupled transport and distribution network system model.

Motivated by the above observation, this letter aims to develop a risk-captured distributional reinforcement learning solution for a joint routing and charging problem in the transportation-energy nexus.The main contributions of this letter can be summarized as: 1) An intelligent decision-making strategy with probabilistic self-adaptability features is designed to capture the system dynamics of coordinated transportation and distribution network.2) Some key characteristics of C51 algorithm are analyzed and derived to ensure the good enough performance for the joint EV routing and charging problem in the uncertain MDP environment.

Problem formulation: An expanded transportation network presented in [6] is used to model the EV driving and routing behavior,which could be further coordinated with the distribution network with consideration of promoting renewable energy as charging power source.Taking as example a simple networkG(V,E) in Fig.1.

Fig.1.The original (solid line) and expanded (dashed line) network.

It only has a single origin-destination (OD) pair,g=(o,d).The edges in edge set E are unidirectional arcs with distance marked besides.The vertices in vertex set V are indexed by numbers in the circles.They denote transportation links (roads) and transportation nodes with charging station available, respectively.The energy consumption in the selected travelling pathgis denoted as λgin the O-D travellingtuple(o,d,).Further more,this network canbe expandedtoa new networkG(V,)byconnecting anytwo nodesby a pseudo edge if they are neighbored to the same node.The transportation network constraints are written as follows:

wherectstands for the per-unit time cost,ξfor the energy consumption of each route distance,ηandprcfor charging efficiency and rated charging power, Q and c for the quadratic and linear cost coefficients of power supply, cCO2for the carbon tax, and crfor the renewable promotion credit (e.g., certified emission reduction).

To quantify the implicit uncertainty characteristics of reward function r caused by the stochastic power output prof distributed renewable energy resources and the driving behavior of routine choice for O-D travelling tuple (o,d,), the reward function r in conventional Markov decision process (MDP) model should be replaced by a random return functionZ.

Definition 1:Zis denoted as the random return or reward value,whose expectation is the normalQvalue function, in the modified MDP model within distributional reinforcement learning framework.

By using such representations, the random return functionZinstead of deterministic straightforward reward value will also be linked to the volatile transition probabilities on top of stochastic definitions of action space and state status space.Following the recursive equation to describeQvalue function, the distribution of random variableZis characterized by the interaction of three other random variableR, the next state-action pair (S′,A′) and its random returnZ(S′,A′).This quantity is called value distribution as the following equation:

Main results: In this section, some sufficient conditions are derived to ensure the applicability of distributional reinforcement learning framework for the well-defined reward maximization problem, where the characteristics of distributional Bellman operator are described.

Next,westatethe following mainresult.Innormal MDPmodel,the conventionalBellman operator Tπandoptimality operatorT∗are dependent on the expectation calculation and usually defined as the following:

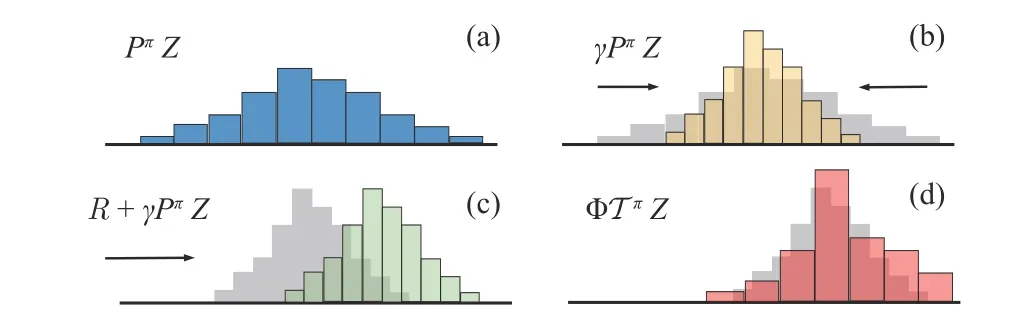
Fig.2.Illustration of distributional Bellman operator for a deterministic reward function: (a) Next state distribution update policy π; (b) Discounting shrinks the value distribution; (c) Reward shifts the value distribution;(d) Projection to the pre-defined support.

Then, the sample loss can be readily minimized using gradient descent.The solution algorithm following such choice of loss and distribution is called categorical algorithm orC51whenN=51 chosen for the number of support atoms.The particular C51 algorithm for the coordinated EV routing and charging problem is presented in Algorithm 1 based on the standard distributional DQN algorithm [7].

Algorithm 1 C51 Algorithm for Coordinated EV Routing and Charging 1: Input A transition Q(xt+1,a)=∑i zipi(xt+1,a)xt,at,rt,xt+1,γt ∈[0,1]2: for random EV SoC a∗←argmaxaQ(xt+1,a)3:4:mi=0, i=0,...,N-1 5: for do ˆT zj ←[rt+γtzj]Vmax j=0,...,N-1 6: with physical constraints b j ←(ˆT zj-Vmin)/∆z 7:l ←■b j■u ←■b j■Vmin 8: ,ml ←ml+pj(xt+1,a∗)(u-b j)9:mu ←mu+p j(xt+1,a∗)(bj-l)10:11: for 12: Output -∑i mi log pi(xt,at)

Numerical example: In the numerical results, a 22-node highway transport network with 6-node of available on-site renewable energy resources is considered in couple with a 14-node 110 kV high voltage distribution network.The transport network is modified from the original 25-node version with detailed information in [8] and similar coupling relationship.The transport network the particular system step-up and model parameters in [6] are used for the simulation with emphasis on the performance of learning-based methods.Some key parameters for C51 algorithm are provided as follows: Set discounting rate γ=0.99, learning rate α=0.001, number of atomsNatoms=51,Vmax/Vmin=±20 and three-layer fully connected neural networks.The simulation results out of multiple runs are summarized in Table 1 with learning performance using C51 algorithm presented in Fig.3.

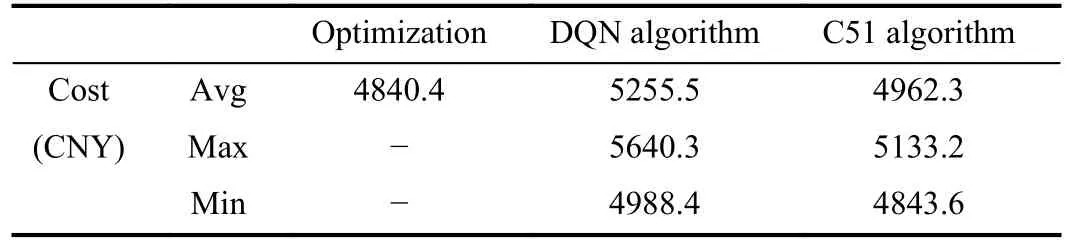
Table 1.The Cost Comparison of Different Solution Methods

We can easily observe that similar to most reinforcement learningbased methods, the distributional categorical method also needs training steps to gradually improve its performance with incremental average return values by sampling the distributional information.As shown in Table 1, although the C51 algorithm mostly outperforms conventional DQN algorithm, it hardly exceeds the upper bound limits calculated from the well-defined optimization method.It can be explained by the facts that in the simulations, we feed the learning algorithm much less input information (e.g., deterministic per-unit time cost) as a prior or assume no ideal prediction (accuracy less than 90%) for the future state estimation (e.g., accurate renewable power output forecasting and guaranteed shortest path).Compared with the results reported in [6] and [8] using similar system setup, the proposed method has slightly higher cost (≤ 0.5%) but with an ultimate gradually improved economic performance in the long-term operation and much less computational cost (≤ 60 s) if using pre-trained reinforcement learning (RL) agent model for online operation directly.Additionally, the C51 algorithm only has an insignificant increase in computational time cost compared with DQN algorithm,costing roughly 30 000 s for 14 000 steps with about 12% more computational load.

In Fig.4, it is shown that most EVs actually indeed give priority to the transportation nodes with renewable energy source powered charging options (e.g., node 5, 9, 14).By tuning the value of green credit token, the weighting of appropriate environmental friendly charging options can overcome the possible tension caused by the increased per-unit time cost due to traffic congestion.

Fig.3.Learning curve for the coordinated EV routing and charging benefit.

Fig.4.EV traffic flows in the coupled transport and distribution network.

Conclusion: In this letter, the coordinated EV routing and charging scheduling problem in transportation-energy nexus is investigated, particularly using an intelligent decision-making strategy with probabilistic self-adaptability features.In order to accommodate the effect of stochastic EV driving and charging behavior on transport network and distribution network, a risk-captured distributional reinforcement learning solution is presented by using explicit probabilistic information for action and reward function in MDP model.

Acknowledgments: This work was supported by National Natural Science Foundation of China (52107079), Natural Science Foundation of Jiangsu Province (BK20210243), and the Open Research Project Program of the State Key Laboratory of Internet of Things for Smart City (University of Macau) (SKL-IoTSC(UM)-2021-2023/ORPF/A14/2022).