A Range-Based Node Localization Scheme for UWASNs Considering Noises and Aided With Neurodynamics Model

Lijuan Wang, Xiujuan Du, and Chong Li

Dear Editor,

This letter focuses on the node localization problem in underwater acoustic sensor networks (UWASNs) with the time-dependent property and various noise disturbances.A range-based localization scheme aided with an integral-feedback-based neurodynamics (IND)model is proposed and referred to as IND-RS, which has the stability against the internal perturbations encountered during the solving process.Considering the complexity of the underwater environment, the Kalman filter (KF) algorithm is smoothly integrated into IND-RS to well eliminate environmental noises to improve the localization accuracy.Besides, the convergence analyses and robustness proofs on the proposed IND model are furnished.Extensive simulations in different localization scenarios are conducted to substantiate the superiority of IND-RS in terms of high accuracy and strong stability.

In UWASNs [1], [2], localization is a fundamental and critical technology.Range-based schemes from the time difference of arrival(TDoA) measurement provide a high localization precision and become the preferred option for UWASNs.For instance, in [3], by utilizing TDoA measurements, a non-convex and partially observable solution is presented for underwater vehicle localization.Besides, Sunet al.[4] construct a second-order TDoA algorithm to address the problem of signal drift.In [5], a TDoA-based prediction localization algorithm is designed to achieve high accuracy and energy efficiency.

Although extensive achievements have been gained by the above researches, the schemes therein still have limitations.First, due to the complexity of the underwater environment [6], TDoA measurements obtained from the natural world are mingled with bias, which grossly decreases the localization accuracy, but was not raised in these studies.In addition, given that the node may move passively or in a controlled manner, the localization problem in UWASN is essentially time-dependent, which indicates that static schemes would introduce lagging errors due to the lack of time derivative information of dynamic parameters.

It has been verified that the zeroing neurodynamics methodology which is originated from the recurrent neural network (RNN), is qualified for dealing with a variety of mathematical and engineering problems [7], [8].Therefore, owing to the efficient real-time computation ability, an IND model is proposed for the node localization in this letter.Furthermore, given the fact of the inevitable perturbations during the solving process and inspired by the noise-tolerance mechanism in cybernetics, an integral-feedback term is incorporated into the proposed IND model to effectively offset the perturbation error.In addition, the KF algorithm is introduced to weaken the impact of environmental noises and improve the accuracy of TDoA measurements [4].Hence, the motivation of this letter is to construct a rangebased node localization scheme in UWASNs from TDoA measurements with the capabilities of real-time computation and resistance to both environmental and internal noises and disturbances.

Problem formulation: Consider an underwater scenario in which a target moves along a trajectory andnneighboring anchors are randomly deployed and fixed, of whichn≥4 for the 2-dimensional (2D)case andn≥5 for the 3-dimensional (3D) case.For the 3D case, the coordinates ofnanchors and the target are defined as

According to the meaning of TDoA, we have the following equations:

wherei∈{1,2,...,n};ri(t) represents the distance between the target and theith anchor;ri1(t) denotes the distance difference from the target to theith and first anchors;Ti(t) stands for the time of the signal traveling from the target to theith anchor;vis the propagation speed of acoustic signals; ∆Ti1(t) signifies the time difference of the signal traveling from the target to theith and first anchors separately.By several derivations, the node localization problem from TDoA measurements in the 3D scenario is expressed as

Design of IND-RS: Firstly, IND-RS adopts the KF algorithm to filter TDoA measurements to compensate for the measured bias which can be deemed as an additive Gaussian white noise.Then, the filtered results would be the input of the proposed IND model to solve the node localization problem (2) and determine the position of the target.

Filtering of TDoA measurements: With the biased TDoA measurements, the core procedures of the KF algorithm are described as follows:

where superscriptTdenotes the transpose operator;ς ∈{1,2,...,M}is the iteration index of the KF;xˆ represents the estimate of TDoA measurements;zsymbolizes the biased TDoA measurements; the definitions ofI,K,A,Q,Randpare regular, thus omitted.Afterwards,xˆM,Mis used as the input to the following IND model.IND model: IND model is proposed for solving the node localization problem (2) with high effectiveness and high accuracy.

First of all, a dynamic error function of (2) is defined as

Whene(t)approacheszero,the obtainedsolutionu(t)approaches the theoretical solutionu∗(t).To thisend,theevolutionfore(t)is designed as

where parametersk1,k2>0 aiming at regulating the convergence rate ofe˙(t) which denotes the derivative ofe(t).Further, by expanding (4), the proposed IND model is obtained

whereA†(t) denotes the pseudoinverse of matrixA(t).

Theoretical analyses:

Robustness analyses: Theorems 2 and 3 are provided to investigate the robustness of IND model (5) against constant and random perturbations, respectively, during the solving process of the node localization.To lay a basis for further investigation, the disturbed IND model is generated as follows:

whereϱ(t)∈Rn-1denotes the unknown perturbation encountered during the solving process, such as the constant implementation error, the random perturbations, or their superposition.

Theorem 2: When undergoing the constant perturbationϱ(t)=ϱ ∈Rn-1during the practical solving process of the node localization problem (2), the disturbed IND model (8) globally converges to the theoretical position of the target, i.e., the residual error ||e(t)||2of the disturbed IND model (8) globally converges to zero.

Proof: By Laplace transform, theith subsystem of the disturbed IND model (8) is deduced

then,

Experiments: In this part, the true path of the target node is signified by TP, and the estimated path is signified by estimated path(EP).

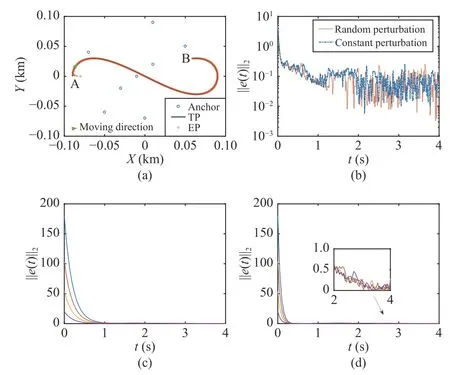
Fig.1.Validation results of the node localization using IND-RS under different perturbation workspaces in the 2D scenario.(a) TP and EP; (b) Residual error ||e(t)||2 with ϱ(t)=[5]6×1 and ϱ(t)∈[4,6]6×1 ; (c) Residual error ||e(t)||2 with k1=5 and k2=5 under the zero perturbation workspace; (d) Residual error | |e(t)||2 with k 1=15 and k 2=15 under the zero perturbation workspace.

Fig.2.Validation results of the node localization using IND-RS under different perturbation workspaces in the 3D scenario.(a) TP and EP; (b) Residual error | |e(t)||2 with ϱ (t)=[5]4×1 and ϱ (t)∈[4,6]4×1.

For a 3D scenario with the range of 0.2 km ×0.2 km ×60 m shown in Fig.2(a), IND-RS is capable of quickly locating the target from a rough and initial position [0.05;0;0]km and tracking it accurately.As depicted in Fig.2(b), the residual error ||e(t)||2converges within 2 s for both the constant perturbation ϱ (t)=[5]6×1and the random perturbation ϱ (t)∈[4,6]6×1.

Comparative results: For comparison, the disturbed model without the integral term is given as follows:

Obviously, the path estimated by the model (14) in Fig.3(a) is deviated from the true path when compared with paths estimated by IND mode (8) shown in Figs.3(b) and 3(c).However, as shown in Figs.3(b) and 3(c), a few of fluctuations are observed in the process of locating the target.As a further exploration, two anchors are added into the scenario.Fig.3(d) shows that the estimated path generated by IND model (8) with the aid of 7 anchors is perfectly completed.From this result, it can be concluded that an appropriate distribution of the anchors can contribute to the localization accuracy of the proposed IND-RS scheme.

Fig.3.Comparative results of the node localization using model (14) and IND model (8) to aid IND-RS under different perturbation workspaces in the 3D scenario.(a) TP and EP of model (14) with ϱ (t)=[5]4×1 and n =5; (b) TP and EP of IND model (8) with ϱ(t)=[5]4×1 and n=5; (c) TP and EP of IND model (8) with ϱ(t)∈[4,6]4×1 and n=5; (d) TP and EP of IND model (8)with ϱ (t)=[5]6×1 and n =7.

Conclusion: This letter has investigated the node localization problem in UWASNs from a dynamic perspective.Given that the underwater environment is fragile and complicated, the KF algorithm and IND model (5) have been employed to establish a new range-base scheme, i.e., IND-RS, with high accuracy and strong stability.Rigorous theoretical analyses and simulative experiments have been provided to verify the effectiveness and feasibility of IND-RS for node localization in the presence of various kinds of noise or perturbations.

Acknowledgments: This work was supported in part by the Innovation Team Foundation of Qinghai Office of Science and Technology (2020-ZJ-903) and the National Natural Science Foundation of China (61962052).