GraphCA: Learning From Graph Counterfactual Augmentation for Knowledge Tracing

Xinhua Wang, Shasha Zhao, Lei Guo, Lei Zhu, Chaoran Cui, and Liancheng Xu

Abstract—With the popularity of online learning in educational settings, knowledge tracing (KT) plays an increasingly significant role.The task of KT is to help students learn more effectively by predicting their next mastery of knowledge based on their historical exercise sequences.Nowadays, many related works have emerged in this field, such as Bayesian knowledge tracing and deep knowledge tracing methods.Despite the progress that has been made in KT, existing techniques still have the following limitations: 1) Previous studies address KT by only exploring the observational sparsity data distribution, and the counterfactual data distribution has been largely ignored.2) Current works designed for KT only consider either the entity relationships between questions and concepts, or the relations between two concepts, and none of them investigates the relations among students, questions, and concepts, simultaneously, leading to inaccurate student modeling.To address the above limitations,we propose a graph counterfactual augmentation method for knowledge tracing.Concretely, to consider the multiple relationships among different entities, we first uniform students, questions, and concepts in graphs, and then leverage a heterogeneous graph convolutional network to conduct representation learning.To model the counterfactual world, we conduct counterfactual transformations on students’ learning graphs by changing the corresponding treatments and then exploit the counterfactual outcomes in a contrastive learning framework.We conduct extensive experiments on three real-world datasets, and the experimental results demonstrate the superiority of our proposed GraphCA method compared with several state-of-the-art baselines.

I.INTRODUCTION

THE development of computer science and artificial intelligence has promoted the progress of the education industry.Many computer-assisted education applications have been developed rapidly, especially, large-scale online education.More and more researchers are paying more attention to developing learning strategies to help improve their learning effect and efficiency in online learning [1], [2].Though a large scale of students’ learning data can be collected, conducting effective personalized knowledge tracing (KT) in the online scenario is a challenging task due to its inherent data sparsity issue.That is, most students solely answered a small number of questions in history, leading to inaccurate student and question representation learning for KT.

Recently, several studies have been focused on addressing the data sparsity issue of KT.For example, Pandey and Karypis [3] focus on solving the data sparsity problem of KT by only leveraging the students’ past activities that are relevant to the given knowledge concept (KC), where a self-attention based approach is proposed.Wanget al.[4] propose a novel deep hierarchical knowledge tracing (DHKT) model,which solves the data sparsity problem by using the hierarchical information between questions and concepts to obtain only the rich relationships between questions and concepts.Yanget al.[5] utilize the graph convolutional network (GCN) to capture the inter-question and inter-concept abundant relations and propose a graph-based knowledge tracing interaction model to mitigate the data sparsity in KT.Chenet al.[6] provide prerequisite relationships between concepts for KT by incorporating the knowledge structure information and creating links between questions for dealing with the data sparsity problem.

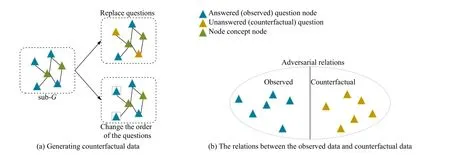
Fig.1.An illustration of modeling unobserved data from a counterfactual perspective.

However, the data sparsity issue in KT is still unsolved, due to the following limitations of existing methods: 1) Existing methods for solving the data sparsity issue omit the usage of counterfactual data.Counterfactual data refers to the interactions that have not happened, but could, would, or might under differing conditions [7].Following its definition in causal inference, we can further deem this kind of data as an augmentation of the observed data, providing us with an efficient way to confront the data sparsity issue.The relations between the observed data and counterfactual data are shown in Fig.1(b).The motivation we leverage the counterfactual technique is that it provides us with an effective way to model the counterfactual data, which further helps us alleviate the data sparsity issue in KT modeling.Counterfactual data is a kind of interaction behavior that is not observational in the past, as one student can only interact (the observed) with one question at the same time.Although the counterfactual data is not observational, it may contain useful information.For example, if we know two questions examine similar knowledge points, and the answer for one of them has been recorded, then, we can deduce similar answers to the other one.By doing this, we can augment the answer records of students to alleviate the data sparsity issue.Intuitively, modeling the counterfactual world enables us to consider more unobserved characteristics of students, and thus can learn more accurate representations for both students and questions.Motivated by the work in [7], we generate the counterfactual data for every student according to the following strategies (as we have shown in Fig.1(a), and more details can be seen in Section III-D): The question replacement operation and counterfactual disruption.The example of the resulting sub-graph is shown in Fig.1(a).Counterfactual transformation can be seen as one kind of data augmentation method.2) Another limitation of existing works is that existing studies fail to capture the structure information among multiple entities, i.e., the relationships among students, questions, and concepts.And,as the students can only interact with a small number of questions (data is sparse), directly modeling them is infeasible.One intuitive way of dealing with this issue is to resort to other relationships among different entities.However, previous works only consider either the entity relationships between questions and concepts, or the relations between two concepts, and none of them investigates their relationships,simultaneously.To overcome this challenge, we further consider the student-question relationship in a unified graph.We incorporate students into the graph to further consider the student-question-concept relationship mainly because students’knowledge state can be modeled by the questions that they have answered.Though some questions may have the same concepts, we can still distinguish the students by their different answers to these questions, as we present students not only by the questions, but also by their answers to the questions.The more information involved with a student we have, the more likely we are to better modeling students.As the direct connection with students only involves questions, incorporating concepts would not increase the combinatorial space.Instead, further considering the concepts, enables us to learn more accurate question representations, which will further affect students’ representation learning.Modeling students,questions, and concepts in a unified graph facilitates us in learning their high-order relationships.An example of modeling them in a unified graph is shown in Fig.2.

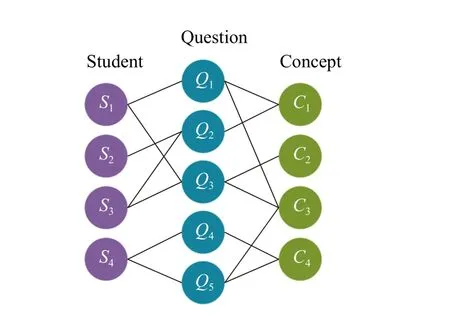
Fig.2.An example of modeling the relationships among students, questions, and concepts in a unified graph.

To overcome the above limitations, we propose a counterfactual graph counterfactual augmentation method for knowledge tracing, namely GraphCA.Our main idea to confront the data sparsity problem is to model the counterfactual data distribution rather than solely the observational data distribution.Specifically, we aim to answer the following counterfactual question, “what the student representation would be if we intervene on the observed answers”.More concretely, given the observed question sequence, we first unify students, questions, and concepts in a student-question-concept (SQC) relation graph to model their higher-order relationships.Then, we intervene on the observed answers by generating interrupted sub-graphs, from which we can obtain counterfactual student representation via counterfactual contrastive graph learning.In counterfactual learning, we perform counterfactual graph transformations from two views based on two factual observations.First, the student’s knowledge state represented by the question sequence may remain similar even if we replace them with similar questions.Motivated by this, we obtain counterfactually positive user representation by randomly replacing similar questions within the question sequence.Second, the student’s knowledge state is independent of the question orders that the student has answered.As such, we achieve the counterfactually positive samples by randomly changing the order of the questions.The goal of our counterfactual strategies is to answer two “what if...” questions.The first strategy that intervenes with the students by the question replacement operation tends to answer “what the student representation would be if we intervene on the observed answers”.The section strategy that disrupts students’ answer records by changing their answer orders tends to answer“what the student representation would be if...”.We resort to the counterfactual learning technique to generate the augmented data mainly because it provides us with an efficient way to explore the unobserved data, which was seldom investigated in previous works.Another reason we leverage counterfactual learning as our solution is that the augmented data can help us to answer the “what if...” questions under the potential outcome framework, which cannot be guaranteed by other related methods.In both cases, we reach the negative representation by directly corrupting the student’s original representation (the details can be seen in Section III-E-3).Then, to effectively learn a more stable user representation,we further conduct contrastive learning between the observational and the counterfactual user representations.That is, by contrast with such out-of-distribution hard negative samples,the learned representations are potentially more stable, since they are less sensitive to noisy questions.Moreover, contrasting with out-of-distribution positive samples potentially makes the learned representations more accurate, since they trust the indispensable samples more.

The main contributions of this work are summarized as follows:

1) We focus on the data sparsity issue of knowledge tracing and solve it by leveraging the counterfactual data in an innovatively devised counterfactual contrasting graph learning method, namely GraphCA.More concretely, we first obtain the counterfactual positive samples by generating interrupted sub-graphs based on two observational facts, and then learn an enhanced user representation by a contrastive graph learning method.

2) We consider the multiple relationships among students,questions, and concepts in a unified heterogeneous graph to enhance the representations of students by the concepts involved in questions.

3) We conduct extensive experiments on three real-world datasets, and the experimental results demonstrate the superiority of our method compared with several state-of-the-art baselines.

II.RELATED WORK

In this section, we briefly review existing works on traditional KT, graph-based KT, contrastive learning-based KT,the studies that solve the data sparsity issue in KT, and Heterogeneous graph neural networks.Then, we review and discuss the counterfactual learning that is related to our research.

A. Traditional KT Methods

Traditional KT methods can be classified into three categories, i.e., cognitive diagnosis models (CDMs), Bayesianbased methods, and RNN-based methods.

1)Cognitive Diagnosis Model: Cognitive diagnosis model(CDM) is a technique that classifies learners’ mastery of knowledge concepts through their answer records [8], which can be further divided into two categories, i.e., continuous and discrete modeling methods [9].As for continuous models,Deonovicet al.[10] propose an item response theory (IRT)-based method to describe the students’ comprehensive knowledge state.However, IRT-based methods only consider the static proficiency value of students, which is insufficient for tracing students’ dynamic knowledge.As for discrete models,De La Torre [11] introduce aQmatrix (question-concept matrix) with each dimension representing the student’s mastery of the knowledge concept to model Deterministic Inputs.But this work suggests that students’ abilities are static, which is inconsistent with the reality that students’ abilities are dynamic and changing.

2)Bayesian-Based Methods: In this category, Bayesian knowledge tracing (BKT) [12] is the first work that investigates knowledge tracing by devising a BKT-based method,where a hidden Markov model (HMM) is utilized to model the learner’s knowledge mastery level and a set of binary variables to model student’s knowledge states.In previous studies on BKT [13], [14], a common approach is to introduce learning parameters such as the probability of student guesses and errors, the difficulty of the question, the ability of the student,and the learning rate of the learner, to learn more information about the student’s learning process.However, the disadvantage of the BKT-based approach is that it assumes that once a student learns a concept, he/she will never forget it [15].But in fact, students’ learning process is usually accompanied by severe knowledge forgetting.

3)RNN-Based Methods: Existing methods in this category often tackle KT as a sequential modeling task [16]–[18].For example, Piechet al.[18] propose a deep learning-based knowledge tracing (DKT) model by using a recurrent neural network (RNN) to track students’ knowledge states.Zhanget al.[19] propose a dynamic key-value memory network(DKVMN) model to study students’ mastery level of each concept.Nagataniet al.[20] further add students forgetting information based on DKT to enhance the performance prediction for students.Abdelrahman and Wang [21] propose sequential key-value memory networks by unifying the recurrent modeling capability of DKT and the memory capability of DKVMN to model student learning.Liuet al.[22] take into account the student’s exercising records and the text content of corresponding exercises by a bidirectional long short-term memory (LSTM) to learn student representations.However,this kind of method mainly focused on modeling students’learning sequences, and the high-order relationships between questions and concepts are ignored.

B. Graph-Based KT Methods

To model the high-order relationships between questions and concepts, researchers have leveraged the power of graph neural network for KT [23]–[26], which have achieved great success in many areas, such as recommender systems [27],computer vision [28], and natural language processing [29].For example, Liuet al.[30] propose a graph-based pre-training approach by considering question-question, question-concept, and concept-concept relationships in a bipartite graph to enhance the representations of questions.Nakagawaet al.[31]propose a GNN-based knowledge tracing method, which defines the knowledge structure as a graph to transform the KT task into a time-series node-level classification problem in the GNN.Yanget al.[5] propose a graph-based interaction model for knowledge tracing model by using GCN to incorporate the relationship between questions and concepts while considering the historical state of the whole exercise.Tonget al.[32] utilize multiple relations of knowledge structures to explore the relationships between concepts and consider both temporal and spatial effects to achieve modeling transfer of knowledge.However, graph-based approaches only consider the entity relationships between questions and concepts, or between two concepts, and none of them investigates the relations among students, questions, and concepts, simultaneously.

C. Contrastive Learning-Based KT Methods

Contrastive learning is a type of self-supervised learning method that aims at learning more robust and accurate representations by pulling similar representations closer and pushing away dissimilar representations.Contrastive learning has achieved significant improvements over traditional methods in the area of natural language processing [33], [34], computer vision [35], [36], and recommender systems [37], [38].For example, Hassani and Khasahmadi [39] introduce a selfsupervised approach by comparing two structural views of the graph to learn node and graph level representations.Hafidiet al.[40] propose a graph contrastive learning framework by maximizing the similarity between the representations of two mapping methods for the same node to learn node embeddings.Recently, several works have also been focused on developing contrastive learning-based solutions for KT.For example, Songet al.[41] propose a contrastive learning framework to obtain the effective representation of knowledge states and improve the ability to predict learners’ performance.Leeet al.[42] use multiple transformers to encode students’ learning history and design bidirectional encoders within a contrastive learning framework to reflect useful selfsupervised signals of historical features.However, none of the existing methods solves KT by contrastive learning from a counterfactual learning view, and its effectiveness needs to be further explored.

D. Methods Solving Data Sparsity in KT

We notice that there are some related works that have been focused on solving the data sparsity issue in KT.For example,Chenet al.[6] deal with the data sparsity problem by incorporating knowledge structure to obtain prerequisite relationships between concepts.Pandey and Kargpis [3] identify the knowledge concepts from the student’s past activities by a selfattention network.Wanget al.[4] solve the data sparsity problem by using the hierarchical information between questions and concepts and only obtaining the rich relationships between questions and concepts.Yanget al.[5] mitigate the data sparsity problem by defining the relationship between questions and concepts on the graph to explore the higherorder information.Leeet al.[42] use contrastive learning to conduct knowledge tracing and propose four data augmentation strategies (CL4KT) to model students’ knowledge states.But their strategies are different from ours in the following aspects:1) We conduct the counterfactual augmentations on the basis of graphs, while CL4KT only deals with sequential data,where the connections among the entities are ignored.2) We devise a new augmentation strategy to generate positive samples, that is, we define the positive samples by randomly replacing the questions that are similar to existing ones.However, all the existing methods solve the data sparsity issue by only modeling the distributions of observational data, while the unobserved counterfactual data is not leveraged.In light of this, in this work we propose to solve the data sparsity problem by modeling the counterfactual data distribution from a counterfactual perspective rather than solely the observational data distribution.

E. Heterogeneous Graph Neural Networks.

Heterogeneous graph neural network (HGNN) is a kind of graph network that models different types of nodes and links[43], [44].Compared with traditional graphs, hierarchical graphs are more capable of expressing complex and hierarchical relationships.Existing studies on HGNN are mainly focused on link prediction [45], [46], personalized recommendation [47], [48], and node classification [49].For example,Xuet al.[45] propose a topic-aware heterogeneous graph neural network (THGNN) to hierarchically mine topic-aware semantics for learning link prediction of multifaceted node representations.Shiet al.[47] devise a heterogeneous graph neural network for recommendation (HGRec), which obtains node embeddings by aggregating neighbors based on multihop meta-paths and adding attention mechanisms to fuse rich semantics.Zhaoet al.[49] develop a heterogeneous graph structure learning (HGSL) framework, which jointly learns heterogeneous graph and GNN parameters to improve node classification performance.However, none of the above studies pays attention to its power of modeling students’ knowledge state.Inspired by the capability of HGNN in modeling the relationships among different types of entities, we further introduce it to the KT task to learn modeling students, questions, concepts, and their corresponding relationships.

F. Counterfactual Learning

Counterfactuals are a process by which humans substitute unreal conditions or possibilities.A typical counterfactual problem can be described as: “what...would be if...?”.In previous studies [7], [50]–[52], counterfactual learning is usually exploited to address the problem of fairness or improve the robustness of their models.For example, Kusneret al.[51]argue that it is critical to correctly address the causality of fairness by describing the process of designing fairness algorithms with causal inference techniques.Zhanget al.[7]model counterfactual data from item level and interest level to learn accurate and robust user representations.Besides the above applications, counterfactual learning has also been used to address the data sparsity problem in natural language processing (NLP) [53], computer vision (CV) [54], and crossmodal (e.g., visual-verbal) [55]–[57] areas, where counterfactual learning is utilized to provide the data augmentations for modeling training.Abbasnejadet al.[55] propose a counterfactual framework to enrich the data by generating a set of counterfactual examples for addressing the problem of data spurious correlation.Chenet al.[56] propose a model-independent counterfactual sample synthesis training method,which has generated a large number of counterfactual training samples by considering two different synthesis mechanisms of masking critical objects or words.Wanget al.[57] propose the counterfactual cycle-consistent (CCC) framework, which applies counterfactual learning to cross-tasks in order to learn instruction following and generation simultaneously.The data augmentation methods of graph structure are generally categorized as node dropping, edge perturbation, attribute masking,and subgraph-based methods [58]–[60].We notice that there are also studies conducting graph data augmentations by counterfactual learning.For example, Zhaoet al.[61] develop a data augmentation-based link prediction method that creates counterfactual links and learns representations from observed and counterfactual links.But, their work is proposed for link prediction, and the advantage of counterfactual graph data augmentation on KT modeling is still unexplored.In our setting, we follow the definition in [62] proposed by Imbens and Rubin.Then, we can define our counterfactual transformation as one of the data augmentation methods that generate counterfactual data from the unobserved world following the data transformation strategies, by which we can answer the “what...if...”.Moreover, their work does not consider the robustness of the learned representations, which is further investigated in our proposed method by combing it with contrastive learning.

III.METHODOLOGIES

This section first introduces the definitions used in this work, then overviews our proposed KT method, and finally describes each of its components in detail.

A. Preliminaries

Definition 3: Counterfactual learning: LetXbe the set of contexts,Tbe the set of treatments, andYbe the set of outcome values.For a contextx∈Xand a treatmentt∈T, we denote the outcome ofxunder the treatmenttbyYt(x) ∈Y.Ideally, we would need all possible outcomes ofxunder all treatments to learn the causal relationships.However, in reality, only one treatment is applied and thus only one outcome is obtained when a contentxis given.

B. Overview of GraphCA

In this work, we tend to answer the following counterfactual question, “what the student representation would be if we intervene on the observed answers”.As we know, conducting counterfactual learning usually has to explore the following three factors: context, treatment, and outcome, where the context is the given background variable; the treatment is the independent variable, which is randomized; and the outcome is the dependent variable, which is related to treatment.In our method, we treat the student node as the contextX, whether the student’s answering records have been intervened as the treatmentT, and the student’s representation as the outcomeY.To answer “what the student representation would be”, we construct the augmentation views on the basis of two factual observations.Our counterfactual transformation strategies are developed based on existing causal inference theory, and they also follow the SUTVA [62] assumption.The overall architecture of our GraphCA is shown in Fig.3.Specifically, we first find the questions (from unanswered questions) that are similar to the ones she has answered.Then, we disturb her historical answers by the following two strategies: 1) We randomly replace the questions in her historical answer record with similarly unanswered questions to generate the unobserved answer sequence.As we replace the questions with similar ones, we deem the disturbed sequence is similar to the original one.2) Another way to obtain unobserved student answer records is to disrupt the answer sequence of the same question set.As the disturbed answer record has the same question set, we also deem this answer sequence has a similar meaning to the original one.After that, we achieve students’ counterfactual representations by performing a graph convolution layer on the transformed graph, where we treat the counterfactual representations from the above generated answer sequences as positive samples, and their representation transformation forms as negative samples (the details can be seen in Section III-E-3).Then, we further conduct contrastive learning on the original and counterfactual representations to model students more accurately and robustly.

C. SQC Graph Construction

To consider the hierarchical relationships among students,questions, and concepts, we first model them in a unified graph (i.e., the SQC graph), which further serves as the foundation of the counterfactual graph transformation and student representation learning.Specifically, we defineG= {(s,rs,q,rq,c) |s∈S,q∈Q,c∈C} as the constructed graph that models the relationship among students, questions, and concepts,wheres,q, andcdenote the students, the questionq, and the conceptc, respectively.rsandrqindicate the relationships between the student-question and the question-concept,respectively.In SQC, there are three types of nodes, i.e., students, questions, and concepts, and two kinds of edges, i.e.,the relationships between students and questions, and the relationships between questions and concepts.For studentsj,questionqh, there is a connection betweensjandqhonly if the student interacts with the question.For questionqhand conceptcl, ifqhcontainscl, we build a connection betweenqhandclto indicate their question-concept relation.

D. Graph Data Augmentation

To alleviate the inherent data sparsity issue in the knowledge tracing task, we resort to the modeling of the counterfactual world, which not only contains observed data but also unobserved data.To provide data foundations for counterfactual learning, we further conduct graph transformations to augment the observed data by the following two transformation strategies.

1)Counterfactual Replacement With Similar Questions: In this work, for each student node (context), the observed data contains only the treatment with true values, and the corresponding outcome of the fact.To answer “what the student representation would be if we intervene on the observed answers”, and obtain the outcome of each student node (context) under different treatments, we intervene with the students by the question replacement operation [63].Moreover,since the answers of each student to the unanswered questions are unknown, we use the result of the nearest observed question as a substitute.Here, the nearest neighbor question refers to the nodes with common concepts in the SQC graph.To construct the counterfactual sub-graphs denoting students’answer sequences, which have similar potential outcomes as the corresponding factual observations, we conduct graph augmentations by the following replacement strategy: 1) We first identify the unanswered questions that are similar to the ones that have been answered by the students.2) Then, we perform graph augmentation on the original sub-graph sub-Gfor each student by randomly replacing the question nodes with the most similar questions as their substitutes (from the sets of unanswered questions).We obtain the nearest nodeqkto the replaced question nodeqiaccording to the following method:

whered(·,·) is used to measure the distance between two nodes.We use cosine similarity to calculate the similarity between two questions, which can express the degree of preference between nodes and learn the degree of similarity between nodes.Its definition is shown as follows:

whereqiandqkare the embeddings of questionsqiandqk,respectively.As we replace the questions with similar ones,we deem that the disturbed sequence is similar to the original one and the student representations we obtained through GCN are similar to the observed student representations.When performing counterfactual replacement, the number of replaced questionsMis set as a hyper-parameter and we fine-tune it in Section VI-B.Note that, if the length of the answer sequence is less thanM, then we replace the question sequence with the same number of answers.

2)Counterfactual Disruption:The counterfactual replacement strategy tends to obtain the unobserved student answer records by replacing already answered questions.But this method also introduces some unanswered questions, which brings uncertainty to our approach.To overcome this challenge, another intuitive way is to disrupt students’ answer records by changing their answer orders, which have the same question set before and after the disturbance.Intuitively, the student’s knowledge state obtained from the same question set should also be similar.More formally, we answer the “what if...” question by finding the potential outcome of each student node on the counterfactual fact that the student answered these questions in different orders, where the treatment is denoted as whether we have changed the students’ answer orders.Then, how to generate the counterfactual data by changing the students’ answer orders is one of our main tasks.That is, we tend to change the order of student’s answers, so that we can obtain the outcome of the student node (context)under different treatments.

Specifically, we conduct the following disruption strategy on the sub-graph: for the same student node (context), we randomly select two question nodes connected with it, and then exchange them on the sub-graph with their relationships remaining fixed.That is, when disrupting the sequence of answers on the sub-G, we only change the question nodes,their relationships with concept nodes and student nodes are unchanged.As the disturbed answer record on the sub-Gstill has the same question set, we can deem this answer sequence has a similar meaning to the original one, and the student representation obtained through the following graph convolutional network is still similar to the observed student representations (the outcome of the context).In experiments, we treat the number of swap question pairs as a hyper-parameter,whose value is set as the half length of the answer sequence if the length of a student’s answer sequence is less than twice the number of swapped question pairs.

E. Inducing Counterfactual Representations With Contrastive Graph Learning

In this work, we leverage the graph convolutional network(GCN) as the backbone of our solution, which provides us with an efficient way to induce the high-dimensional student,question, and concept features from students’ learning graphs.Concretely, two kinds of student representations (i.e., outcomes), i.e., the outcomes before and after the treatment is changed, are learned by two GCNs (the workflow of the learning process is shown in Fig.3).

1)Inferring Representations From the Original Student Learning Graph: In the SQC graph, there are three kinds of nodes, i.e., students, questions, and concepts, and two kinds of edges, i.e., the relationships between students and questions,and the relationships between questions and concepts.Lets,q,andcbe noted as student nodes, question nodes, and concept nodes, respectively.rsandrqindicate the relationships between the student-question and the question-concept,respectively.

a)Concept representation learning:In this work, we represent concepts by the questions that they belong to.For a concept, its representation is learned by aggregating the information from itself and the question nodes connected with it.Formally, we denote the representation of concept nodecmin graphGascmandthe question setthat isdirectlyconnected withit as.Then, wedefine themessage passed fromthe question node settocmin thel-th layer GCN as

After aggregating the message passed from the concept itself and the question, we use aReLUactivation function.The calculation formula of thel-th layer GCN can be defined as

whereReLUis the none-linear activation function.c)Student representation learning: Due to students being only connected with the questions that he/she has answered,the representation of a student is learned by aggregating the information from himself/herself and the corresponding questions.Letsjbe the representation of student nodesj, andbe the neighbor question set.Then, we can define the passed messages from the question nodestosjin thel-th layer as

Similarly to concepts and questions, we arrive at the student’s final representation by aggregating the messages from himself/herself and the corresponding questions

2)Representation Learning on the Transformed Counterfactual Graph: As described in Section III-D, we obtain two augmented sub-graphsby performing counterfactual graph transformations to achieve the outcomes of our experiments when the treatment is changed.Correspondingly,we can achieve two types of student representations by the same GCN encoder, which are further treated as the counterfactual outcomes of students’ learning states.

a)Student representation learning with counterfactual replacement: As in the transformed counterfactual graphG1,student nodes are only connected with the questions that have been answered by the students, we can denote the representation ofsjby aggregating the messages from questions.We letbe neighbor question set.The message is denoted as

By integrating the above messages, we can define the student representation as follows:

b)Student representation learning with counterfactual disruption: Similarly to the counterfactual graphG1, the messages that are passed to studentare also from himself/herself and the questions that he/she has answered.The message from the question nodes is defined as

3)Enhance Student Representation by Contrastive Learning: To enhance the learned student representations, we further incorporate contrastive learning objectives.As we have described in Section III-D, the student representations induced from the counterfactual graphs indicate similar students’learning states both before and after the treatment is changed,we treat both outcomes as positive representations of students.To make a contrast, for both transformation views, we directly generate the corresponding negative student representations by a destruction function P.It is denoted as

a)Contrast with the outcome of the counterfactual replacement:We consider the outcome of the first counterfactual transformation as the positive sample, and the destructed representation as the student’s negative sample.Then, to minimize the distance between the student’s representation and the positive sample, and maximize its distance with the negative samples, we use InfoNCE [64] with a standard binary crossentropy loss as our learning objective.By doing this, we effectively learn a more accurate and robust representation of the student.Formally, we have

wherendenotes the numbers of students,denotes student representation with counterfactual replacement.fD(·) is the discriminator function that takes two vectors as input and then scores them for consistency.We use the dot product between the two representations to achieve discrimination.

b)Contrast with the outcome of the counterfactual disruption: In this counterfactual disruption view, we also treat the outcome of the counterfactual transformation as positive samples, and students’ destruction as negative samples.

By performing InfoNCE loss, we can get the second contrastive learning objective function

F. Learning Objectives

1)Recommendation Loss: To make predictions for the target questionqt, we first combine its representationqtwith the student presentationsN, and then map them through a neural network to a low-dimensional embedding, so as to calculate the probability that the student answers the target question correctly

whereW2,W3,b2,b3are the model parameters, σ(x) is the sigmoid function, ⊕ is the concatenation operation andpN+1is the probability that the student answers the question correctly at StepN+ 1.

The cross-entropy loss is utilized to calculate the prediction loss by the above recommender (i.e., (22))

2)Objective Function: To further consider the accuracy and robustness of students’ representations, we then train the recommendation loss and the contrastive losses, jointly.That is,we achieve our final objective function by aggregating (23),(20), and (21)

whereαandβare hyper-parameters to control the magnitude of the contrastive learning, Lcrand Lcodenote the contrastive losses of counterfactual replacement and counterfactual disruption, respectively.Lcrand Lcoare interpreted as maximizing the mutual information between the student representations learned in the two counterfactual transformation strategies.To learn the parameters, the gradient descent method is exploited.The computational complexity of our method mainly contains two parts.The first one is in finding the nearest neighbor question nodes, which needs to calculate the node-to-node distance to find the nearest neighbor node of the question node, and its computational cost isO(m2).The second one is in training the counterfactual learning model,which costsO(LH2m) to train the GCN encoder.HereLis the number of GCN layers, andHis the size of the node representation.

IV.EXPERIMENTAL SETTINGS

In this section, we first introduce our research questions and the three real-world datasets, and then describe the evaluation protocols, relevant baselines, and implementation details of our proposed approach.

A. Research Questions

We evaluate our proposal by answering the following research questions:

RQ1: How does our proposed GraphCA approach perform compared with other state-of-the-art KT methods?

RQ2:How do the student representations benefit from modeling the counterfactual world and contrastive learning?

RQ3:How do the hyper-parameters (i.e.,M,N, andd) affect the performance of GraphCA?

RQ4: What are the training efficiency and scalability of GraphCA when processing large-scale data?

B. Datasets and Evaluation Protocols

To evaluate the performance of our proposed method, we use the following three real-world datasets.We report statistics for the ASSIST2009, ASSIST2012, and Algebra2006 datasets in Table I.For each dataset, we use 80% of the data as the training set and 20% of the data as the test set [3], [5].

ASSIST2009: This dataset is collected from the ASSISTments online education platform [65], which is widely used for KT.The education system can help students solve problems and improve their learning abilities.For this dataset, we remove records without concepts.This dataset has 3241 students, 17 709 questions, 124 concepts, and 278 868 records.

ASSIST2012: This dataset is collected from the same platform as ASSIST2009.The processing of the dataset is also in the same way as ASSIST2009.This dataset has 29 018 students, 53 086 questions, 265 concepts, and 2 711 602 records.

Bridge Algrbra2006: Bridge to Algebra 2006-2007 stems from the KDD Cup 2010 EDM Challenge [66].This dataset is based on an algebra course on the Cognitive Algebra Tutor System.This dataset has 1130 students, 129 263 questions,550 concepts, and 1 817 393 records.

We adopt two commonly used evaluation metrics, areaunder the curve (AUC) [31] and accuracy (ACC) [67], to measure the performance of the GraphCA.AUC is the area under the receiver operating characteristic (ROC) curve.ACC represents the error between the true value and the predicted value.When the value of AUC or ACC is 0.5, it indicates that the model performs as well as the random guess.A larger value of AUC or ACC indicates a better predictive performance of the model.

TABLE I STATISTICS OF THE DATASETS

C. Baseline Methods

To validate the effectiveness of our model, we compare our GraphCA with the following baseline methods.

BKT[12]: This is a knowledge tracing model based on a Bayesian network, which exploits HMM to model students’knowledge state as a set of binary variables.

DKT[18]: This is the first knowledge tracing model based on a deep neural network, which uses RNN to model the learning situation of students.The input of DKT is the one-hot encoding of the student’s knowledge representation and the output is a vector representing the degree of learner knowledge mastery.

DKVMN[19]: This typical model utilizes the idea of the memory-enhanced neural network, by using a static matrix key to store all knowledge concepts and a dynamic matrix value to store and update the student’s knowledge state.

GKT[31]: This is a GNN-based knowledge tracing model which converts knowledge states into graphs for the prediction of student situations.At each time step, GKT updates the new state by aggregating the states of neighbors, and the states of neighbors are also updated.

SAKT[3]: This is a knowledge tracing model based on selfattention.SAKT accomplishes the prediction task by selecting more relevant KCs from the student’s past activities.

AKT[68]: This is an attention-based network for knowledge tracing, and models learners’ past performance by constructing context-aware representations for questions and responses.

GIKT[5]: This is a graph-based knowledge tracing interaction model that utilizes GCN to capture the rich relationships between questions and concepts.GIKT takes into account the interaction between the student’s current state, the student’s history states, the target question, and relevant concepts.

CL4KT[42]: This is a knowledge tracing model based on contrastive learning, which proposes four data augmentation methods thus capturing an effective knowledge state representation.

To better illustrate the characteristics and hierarchy of these models, we compare the different models in Tables II and III.Among them, only the GIKT and our GraphCA model consider both direct and indirect relationships between concepts.For graph-based KT models GKT, GIKT, and GraphCA, GKT contains only concept nodes, i.e., the model considers only the relationship between concepts; GIKT contains both question and concept nodes, i.e., the model considers the relationship between questions and concepts and between concepts; in addition to the above two types of relationships, the GraphCA model takes into account the student-question relationship by introducing unified graphs involving students, questions, and concepts as multi-entities.

TABLE II CHARACTERISTICS OF THE COMPARISON METHODS

TABLE III THE CONSIDERED ENTITY RELATIONSHIPS

D. Implementation Details

We implement GraphCA using the TensorFlow framework accelerated by NVIDIA RTX 2080 Ti GPU.By conducting extensive experiments, we obtain the optimal parameters for GraphCA.During the training process, we use the Adam algorithm [69] to optimize the parameters of our model, the learning rate is 0.001, and the mini-batch size is 64.For hyperparameters, the number of replacement questionsMis 5; the number of pairs of swap questionsNis 5; the embedding sizes of students, questions, concepts, and answers are all set tod=100.The details of tuning the hyper-parameters are shown in Section VI-B.We also use dropout [70] with the probability of 0.8 to prevent overfitting.

V.EXPERIMENTAL RESULTS (RQ1)

We compare the proposed GraphCA with existing methods on different datasets.We evaluate the performance of each model by measuring the AUC and ACC.As shown in Table IV,we report the results between baseline models and our GraphCA for the two classification metrics on the three datasets.In our evaluation phase, we run all the experiments ten times with the same parameter settings and report theiraverage values.To clearly show the significance of our improvements, all the comparison results also include their standard deviations.The best results for AUC and ACC on different datasets are shown in bold.As can be seen from the results, our model achieves high performance in most metrics on the three datasets.On the ASSIST2009 dataset, the AUC value of the GraphCA model is 79.0%, the AUC value of the GIKT model is 77.9%, and the AUC value of the AKT model is 78.3%.On the ASSIST2012 dataset, the AUC value of the GraphCA model is 77.8%, which is slightly better than the AKT and GIKT models.On the Algebra2006 dataset, the AUC value of the GraphCA model is 78.6%, the AUC value of the GIKT model is 77.8%, the AUC value of the CL4KT model is 77.3%, and the AUC value of the GKT model is 74.8%.

TABLE IV COMPARISON RESULTS ON ALL THREE DATASETS IN TERMS OF AUC AND ACC

In all the baselines, the deep learning-based model has better performance than the traditional BKT model, which demonstrates the effectiveness of deep learning methods for predicting student performance.The SAKT model performs better than the DKT and DKVMN, which indicates that it is important to consider the relevance between the next question and the student’s past activities.In addition, both models,GKT and GIKT, use the existing knowledge structure to obtain more additional useful information.From Table IV, we can find that the prediction results of GKT and GIKT are relatively better compared with other baselines.Furthermore, our model not only considers the relationship between questions and concepts but also includes the relationship between students and questions, which suggests that modeling multiple entities facilitate the predictive performance of the model.

VI.MODEL ANALYSIS

A. Ablation Study (RQ2)

To better understand the role of the different building blocks in the GraphCA, we conduct ablation experiments to illustrate the effect of each part of our model on the prediction results.We build the GraphCA-RCRO (Remove counterfactual transformation module for both views), GraphCA-RCR (Remove graph transformation module for counterfactual replacement),GraphCA-RCO (Remove graph transformation module for counterfactual disruption), and GraphCA-RCL (Remove contrastive learning) architectures by removing the counterfactual transformation module and contrastive learning module.The results of the four architectures on the ASSIST2009 dataset, ASSIST2012 dataset, and Algebra2006 dataset are shown in Table V.

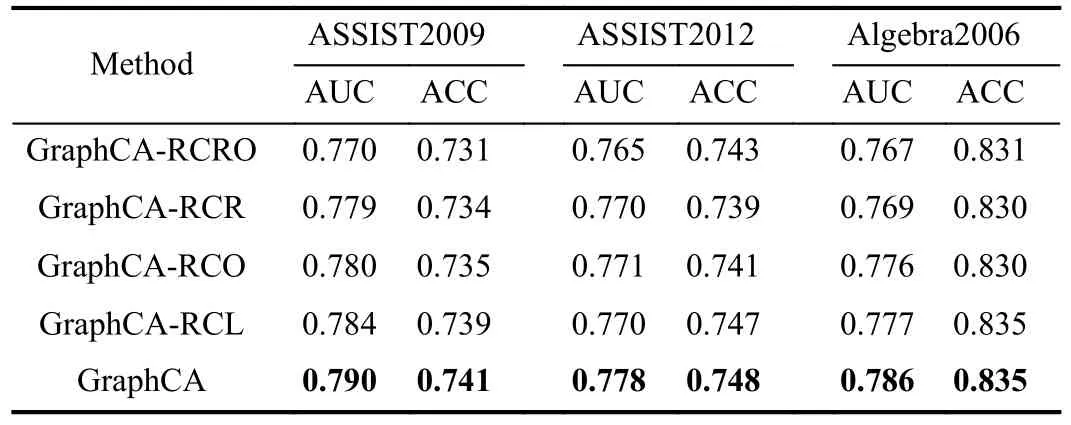
TABLE V ABLATION STUDIES BY CONSTRUCTING DIFFERENT ARCHITECTURES

GraphCA-RCRO: This suggests that neither counterfactual replacement of graph transformations nor counterfactual disruption of graph transformations are considered.

GraphCA-RCR: This suggests that the graph transformation process of counterfactual replacement is not considered.

GraphCA-RCO: This suggests that the graph transformation process of counterfactual disruption is not considered.

GraphCA-RCL:This suggests that the contrast between the observed and the counterfactual student representation is not considered.

The experimental results are shown in Table V, where the GraphCA model achieves the best performance when performing graph transformation from two views simultaneously.That is, GraphCA has a significant facilitation effect by combining two counterfactual transformation strategies.The above suggests that it is also critical to consider unobserved data when we track students’ learning processes.From the results of GraphCA-RCR and GraphCA-RCO, we see that modeling counterfactual data from two views can improve the performance of the model.In addition, the better performance of GraphCA compared to GraphCA-RCL indicates that the presence of contrastive learning can learn more accurate and robust student representations.The prediction results of eachmodule answer RQ2 while demonstrating the effectiveness of our GraphCA.

To evaluate the performance of our method on sparse data,we further evaluate GraphCA by splitting the dataset into different sub-collections from 20% to 100%, and report the experimental results in Fig.4, from which we can observe that our GraphCA method can perform better than the GIKT method (the most competitive baseline) on all three datasets.This result demonstrates the effectiveness of our counterfactual graph and the contrastive learning method in alleviating the data sparsity issue.

B. Hyper-Parameter Analysis (RQ3)

Our GraphCA model has three highly important hyperparameters: the first is the number of replacement questions when performing the counterfactual transformation, the second is the number of pairs of swap questions when generating counterfactual data, and the last is the size of the embedding dimension.In this subsection, we will investigate the effect of different values of these three hyper-parameters on GraphCA.

1)Impact of M and N: We denote the number of replacement questions asMand the number of pairs of swap questions asN.We conduct experiments on differentMandN,whereMandNare chosen from {1, 5, 10}, to illustrate the impact of hyper-parameters on the prediction performance.From Table VI, we can find that the performance of GraphCA varies smoothly around the peak region, which is because the generated counterfactual data are positive samples and we do not change the semantic representation of the observed student to a great extent.Also, increasing the number of replacement questions and the number of pairs of swap questions may introduce noise because the selection of questions is randomly sampled.Although the performance of our model changes smoothly, we can still observe that the model performs relatively well when bothMandNare 5.

2)Impact of d: We set the embedding dimensionsdof student, question, and concept to be the same.The change in the performance of the model by changing the embedding dimension is illustrated in Fig.5.We setdto {20, 40, 60, 80,100} to illustrate the effect of this hyper-parameter on the prediction performance.From Fig.5, we can find that the prediction performance of our GraphCA becomes better and better as the embedding dimension increases.However, the values of AUC and ACC change very little when the dimensions reach a cer-TABLE VI IMPACT OF PARAMETERSMANDNtain number.In our experiments, we setd= 100.

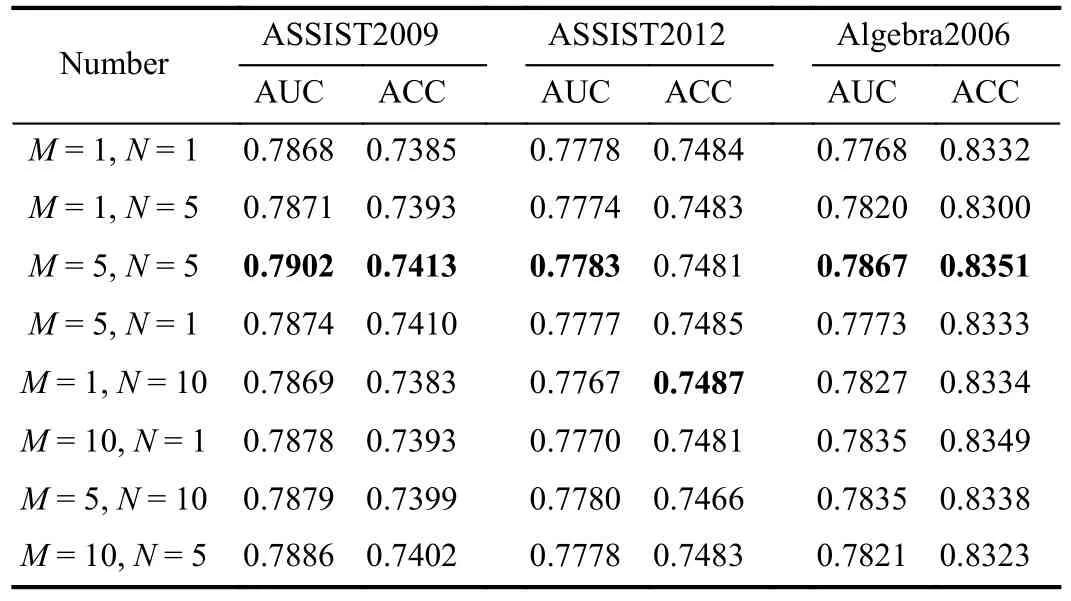
Number ASSIST2009 ASSIST2012 Algebra2006 AUC ACC AUC ACC AUC ACC M = 1, N = 1 0.7868 0.7385 0.7778 0.7484 0.7768 0.8332 M = 1, N = 5 0.7871 0.7393 0.7774 0.7483 0.7820 0.8300 M = 5, N = 5 0.7902 0.7413 0.7783 0.7481 0.7867 0.8351 M = 5, N = 1 0.7874 0.7410 0.7777 0.7485 0.7773 0.8333 M = 1, N = 10 0.7869 0.7383 0.7767 0.7487 0.7827 0.8334 M = 10, N = 1 0.7878 0.7393 0.7770 0.7481 0.7835 0.8349 M = 5, N = 10 0.7879 0.7399 0.7780 0.7466 0.7835 0.8338 M = 10, N = 5 0.7886 0.7402 0.7778 0.7483 0.7821 0.8323

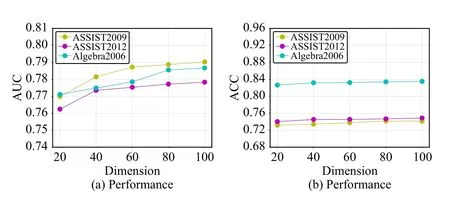
Fig.5.Impact of parameter d.

C. Training Efficiency and Scalability (RQ4)

Fig.6.The training time of GraphCA with different data ratios.

To investigate the training efficiency and scalability of our GraphCA, we measure the time required for different proportions of training data on three real-world datasets.Specifically, we vary the ratio of training data in {0.2, 0.4, 0.6, 0.8,1.0}, and the detailed training time is shown in Fig.6.Furthermore, we also include the linear training time related to the number of training samples to make our experimental results more comparable.The linear training time is calculated according to the linear relationship between the first two training times with linearly increasing the dataset split ratio from 20% to 100%.We term this time as the linear time as we thought the linear scalability of our method should increase linearly with the increase of the dataset ratio.From the experimental results in Fig.6, we can observe that as the proportion of training data increases gradually from 0.2 to 1.0, the training time cost of our GraphCA grows from 0.158×1 03to 0.604×1 03on the ASSIST2009 dataset, from 1.507×1 03to 6.174×1 03on the ASSIST2012 dataset, and from 0.419×1 03to 2.124×1 03on the Algebra2006 dataset.In addition, we can also observe that the actual training time of the model on the ASSIST2009 dataset and ASSIST2012 dataset is less than the linear training time, which demonstrates that the training time of the model is better than we expected.The overall trend on these three datasets indicates that the dependency of times cost for training GraphCA on the data scale is approximately linear.We further compare our method with GIKT (the most competitive method) on all three datasets on the basis of our previous scalability experiments.From the experimental results, we can find that though our method can scale well with the increase of the training data ratio, it has no advantage over the baseline method, due to its additional counterfactual learning cost.

D. Case Study

To make the counterfactual data modeling process of our model more intuitive and understandable, we provide a case study based on the ASSIST2009 dataset.In Fig.7, we select an answer sequence with a student sequence length of 19.The first row is the student’s observed answer records.The question IDs of the observed answer records are {15687, 15711,15704, 15723, 15724, 15719, 15727, 13725, 14498, 13690,17877, 17864, 14625, 14893, 14882, 14278, 14864, 14258,14261}.We obtain the second and third rows of records by counterfactual transformation strategies.For the replacement question operation, we randomly select 5 questions from the observed answer records for replacement.The indexes of the replaced questions are {10, 6, 5, 4, 16}.By the similarity between the questions, we find the nearest neighbor to the replaced question among the unanswered questions.The IDs of the nearest neighboring questions are {1970, 3530, 16899,1403, 3493}.For the third row, we only change the order of the questions, without changing the content of the answers.That is, the second and third rows do not fundamentally change the original student semantic representation, which suggests that the counterfactual transformation strategy mentioned in our model is reasonable.Fig.8 depicts an example of a student’s mastery of five knowledge concepts.From Fig.8 we can find that the student’s proficiency in the pythagorean theorem concept, median concept, and rounding concept increased, while proficiency in the circle graph concept decreased.After answering 19 questions, students mastered the pythagorean theorem concept, the median concept, and the rounding concept, but not the circle graph concept.

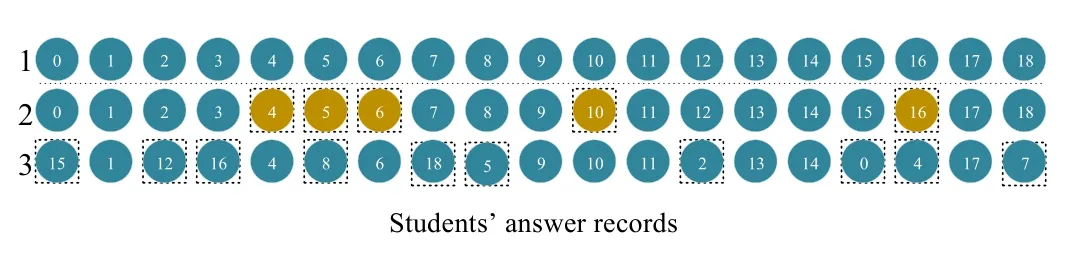
Fig.7.A case study based on the ASSIST2009 dataset.In the first row, we show the observed student answer records, and the second and third rows are the records obtained by the counterfactual transformation of the two views.

Additionally, we find that our method cannot do well for the students with only a few learning interactions.This is mainly because we represent students by their interacted questions in the graph, and when there are only a few records, these questions are not enough to accurately express a student’s knowledge state.To show the limitation of our method, we randomly select a student with only 8 answering records (i.e., the length of the answer sequence is 8), and perform two counterfactual transformation strategies as shown in Section III-D.The student’s knowledge state showing his mastery of knowledge concepts is presented in Fig.9, from which we can observe that by answering fewer questions, we cannot capture the significant change in his/her mastery of the concepts.

VII.CONCLUSIONS AND FUTURE WORK

In this paper, we propose a knowledge tracing method based on GCN.We learn question representations and student representations by constructing the SQC graph.In addition, we perform counterfactual graph transformations from two views based on two factual observations.Then we design contrastive learning objectives to learn accurate and robust student representations.We conduct experiments on three realworld datasets, and the experimental results show that our proposed GraphCA model has better performance.

In the future, we would like to consider different strategies for counterfactual transformation (e.g., changing the number of original student answers) to implement the operations from multiple levels.Otherwise, there might be some more efficient way to obtain negative samples in the contrastive learning process.We also notice that some theories (e.g., learning ability) may affect the results of the KT.

Fig.8.An example of a student’s mastery of five knowledge concepts.

Fig.9.The limitation of GraphCA.