Containment-Based Multiple PCC Voltage Regulation Strategy for Communication Link and Sensor Faults
2023-10-21MeinaZhaiQiuyeSunRuiWangandHuaguangZhang
Meina Zhai , Qiuye Sun ,,, Rui Wang , and Huaguang Zhang ,,
Abstract—The distributed AC microgrid (MG) voltage restoration problem has been extensively studied.Still, many existing secondary voltage control strategies neglect the co-regulation of the voltage at the point of common coupling (PCC) in the AC multi-MG system (MMS).When an MMS consists of sub-MGs connected in series, power flow between the sub-MGs is not possible if the PCC voltage regulation relies on traditional consensus control objectives.In addition, communication faults and sensor faults are inevitable in the MMS.Therefore, a resilient voltage regulation strategy based on containment control is proposed.First, the feedback linearization technique allows us to deal with the nonlinear distributed generation (DG) dynamics, where the PCC regulation problem of an AC MG is transformed into an output feedback tracking problem for a linear multi-agent system (MAS) containing nonlinear dynamics.This process is an indispensable pre-processing in control algorithm design.Moreover, considering the unavailability of full-state measurements and the potential faults present in the sensors, a novel follower observer is designed to handle communication faults.Based on this, a controller based on containment control is designed to achieve voltage regulation.In regulating multiple PCC voltages to a reasonable upper and lower limit, a voltage difference exists between sub-MGs to achieve power flow.In addition, the secondary control algorithm avoids using global information of directed communication network and fault boundaries for communication link and sensor faults.Finally, the simulation results verify the performance of the proposed strategy.
I.INTRODUCTION
AN microgrid (MG) is a small generation, distribution, and consumption system consisting of a collection of distributed power sources, energy storage systems, energy conversion devices, monitoring and protection devices, and loads[1].The control structure of an MG is generally divided into three layers: bottom control, secondary control, and tertiary control.An essential function of the secondary control level is restoring the MGs’ voltage [2].
Secondary control can be categorized as centralized, distributed, or decentralized based on the communication method employed.Centralized control enables complex control with high accuracy and speed, making it suitable for small-scale MGs [3].However, a single point of failure can lead to global control paralysis and reduced reliability.Decentralized control offers fast response time and high reliability but typically lacks accurate global information, resulting in lower control accuracy, susceptibility to interference, stability issues, and limited ability to achieve complex global control objectives[4].Distributed control, leverages communication between neighboring DGs to achieve consensus through mutual information exchange [5], [6].It utilizes a distributed local controller approach instead of a central controller, thus avoiding the single point of failure [7]–[9].The underlying multi-agent system (MAS) consensus algorithm enables each DG to indirectly share global information by communicating only with its neighbors.Reference [10] demonstrates the application of distributed fixed-time and prescribed-time consensus control in the domains of mobile robots and smart grids.Recently, it has become the primary implementation method for secondary control in MGs [11]–[13].In [14], a distributed consensus protocol is developed to solve the accurate reactive,harmonic and unbalanced power-sharing problems in MG.Consensus-based distributed finite-time regulators are proposed in [15] to coordinate active, frequency and output voltage in islanded MGs.In [16], the problem of distributed secondary control of isolated AC MGs in the presence of external disturbances is studied.However, the secondary control strategies [12]–[16] are based on the premise that the components and communication are perfect.
In practical situations, electrical components such as actuators and sensors may experience failures [17]–[19].Two distributed control schemes were proposed by [20], [21], respectively, with fault tolerance for various potential faults in sensors and actuators, thus ensuring voltage and frequency regulation of the closed-loop system.Our previous study [22] proposed a fully distributed event-triggered fault-tolerant secondary control method based on information about neighboring distributed generation (DGs).Each DG requires only local information about itself and its neighbors.To achieve AC MG load voltage regulation, [23] proposed an active fault-tolerant event-driven strategy with unknown actuator faults under discrete communication.However, existing fault-tolerant control strategies applied to MGs generally assume that the communication links are ideal [20]–[23].The communication between DGs is applied in free space, which is susceptible to physical variations in the communication channel and noise from other sources or channel manipulation from hostile nodes [24], [25].To achieve high reliability of MG, resilient control of communication failures has become a critical control issue.Distributed control schemes for implementing frequency/voltage restoration and proportional power sharing considering the communication delay problem are proposed in [26].In [27], a distributed noise-resistant secondary control is proposed for restoring the output voltage and frequency of DG inverter with additive noise.In [28], output voltage and frequency regulation in scenarios where the communication network suffers from both communication delays and switching topologies are investigated.Reference [29] addresses the challenges of current sharing and voltage restoration in islanded DC MGs under heterogeneous communication delays and denial of service (DoS) attacks, providing a novel solution for the first time.This work tackles the complex issues arising from communication delays and cyber-attacks, ensuring efficient and reliable operation of MGs.Inspired by [30], [31], some valuable results were obtained in MG output voltage and frequency restoration control, in the presence of communication failures [24].
However, the resilience regulation of point of common coupling (PCC) voltage in multi-MG systems (MMSs) under communication link and sensor faults remains an unexplored area of research.Existing methods have several limitations that need to be addressed: 1) Previous works [12], [13], [15],[16], [20]–[22], [24], [26]–[28] primarily focused on restoring the output voltage of each DG unit to its nominal value.However, the co-regulation of PCC voltage in MMS is even more critical than regulating the DG output voltage.It is necessary to develop a reasonable system model that reflects the interaction effects between the communication-based PCC voltage control protocol and the DG units in the MMS.2)Using the conventional consensus tracking method to control the PCC voltages collectively at the reference value would result in no voltage difference between the sub-MGs, thus hindering the power flow between them.Therefore, it is necessary to design reasonable control objectives that address the co-regulation problem of PCC voltages.3) Furthermore, the PCC voltage regulation problem addressed in this paper is an output feedback tracking problem after feedback linearization.However, the reference-based state observer proposed in previous works [24], [30] is not applicable due to the challenges of full-state unmeasurability and sensor failures.Moreover,the directional communication network and the parameters related to communication and sensor failures are unknown,adding further complexity to the resilient control problem.
Based on the above limitations, we study the AC MG containment-based secondary voltage regulation control with communication link and sensor faults.The main contributions of this paper are summarized as follows:
1) Unlike the traditional consensus-based voltage regulation problem [12], [13], [15], [16], [20]–[22], [24], [26]–[28],we introduce the control objective of containment control in this paper.The reason is that it is impossible to achieve power flow between sub-MGs if multiple PCC voltages are controlled collectively at the reference value.Therefore, a containment-based distributed controller is proposed to balance the conflicting objectives of voltage regulation and power flow.This controller makes the PCC voltage control within a reasonable range while there is a voltage difference to achieve power flow.
2) Unlike the output voltage regulation problem [12], [13],[15], [16], [20]–[22], [24], [26]–[28], our goal is the regulation problem of the PCC voltage.The feedback linearization technique allows us to deal with nonlinear DG dynamics.Thus, the PCC voltage regulation problem of the AC MG is transformed into a distributed output feedback tracking problem of a linear MAS with nonlinear dynamics.This transformation is an indispensable preprocessing in the design of the control algorithm.
3) The leader-based observer in [27] and [30], [31] is unavailable due to thexifull-state unmeasurability and sensor fault problems.Therefore, we designed a novel adaptive follower-based observer to handle communication and sensor faults, avoiding the use of global information of directed communication network and fault-related parameters.
The outline of this paper is given below.Section II gives the modeling framework to transform the PCC regulation problem of an AC PCC into a distributed output feedback tracking problem with linear MASs containing unknown nonlinear dynamics.In Section III, some problem statements are made.In Section IV, the main results are established, and a resilient voltage regulation strategy based on containment control is built.Then, Section V verifies the effectiveness of the proposed control method.Section VI concludes this paper.
Notations:LetIN∈RN×Nrepresent theidentitymatrix,λmax(∗)representthe maximumeigenvalueof “∗ ”, //·//represent the Euclidean norm of vector “·” , diag{a1,...,aN} represent a diagonal matrix, col{a1,a2,...,aN} be a column vector,and ⊗ represent the Kronecker product.
II.MODELING FRAMEWORK
Considering an MMS containingNsub-MGs, this paper considers the regulation problem of multi-PCC voltages.A sub-MG consists of DGs.The dynamic model of the DG includes droop control, inner-loop voltage and current control,LC filter, containment-based voltage secondary control, and line model, as shown in Fig.1.
The droop controller dynamics are

Fig.1.Block diagram of an inverter-based DG.
where ωiis the angular frequency of the DG dictated by the primary control,is the reference value for the output voltage magnitude that is provided for the internal voltage control loop of the DG, ωniandVniare the frequency and the voltage input,mPiandnQiare the droop coefficients,PiandQiare measured active and reactive power at terminals ofith inverter, respectively.
The power controller dynamics are
where ωciis the cutoff frequency of the low-pass filters used in measuring power.vodi,voqiandiodi,ioqidenote the direct and quadrature components of the output voltagevoiand currentioi, respectively, of theith inverter.
The voltage and current controller dynamics are

The output LC filter and connector dynamics are
whereRiis filter resistance.vidi,viqiare output components of the current controller.vbdi,vbqiare the components of the PCC voltage.Lci,Rciare inductance, resistance ofthe line between the PCCandtheinverteroutput, respectively.
The nonlinear dynamic model of the AC MG in a compact form is
where the state vector is
andJi=[ωcom,vbdi,vbqi].Detailed expressions forfi(zi),gi(zi),andki(zi) can be extracted from (1)-(4).Moreover,di(zi) is set tovodi.yiis set tovbdi.vlirepresents the voltage of the line between the PCC and the inverter output.
Then, by feedback linearization, we have

It is difficult to obtain the value ofv˙bdiin practice, the design of the control algorithm using onlyvbdiinstead ofxi,wherexiis translated from (7) as follows:
Remark 1: Unlike the traditional output voltagevodiregulation problem in [12], [13], [15], [16], [20]–[22], [24],[26]–[28], we address the PCC voltagevbdiregulation problem for AC MGs.Moreover, due to thexifull-state unmeasurability, the state-based controller cannot achievevbdiregulation.In the input-output feedback linearization (7), repeated differentiation concerning time generates the direct relationship between the dynamics ofvbdi(or equivalentlyyi) and the control inputVni.Thevbdiregulation problem is transformed into a distributed output feedback tracking problem with linear MAS, where the system contains nonlinear dynamicsv¨li.Moreover, an appropriate auxiliary controlleruiis designed so thatvbdiregulation is achieved usingVni.The design of controlleruidepends on state observerxˆi, while the design ofxˆidepends onvbdi.
The containment-based voltage controller for each sub-MGs bound voltages within a reasonable range.The virtual leaders serve as the upper and lower boundaries of the specified voltage, as follows:
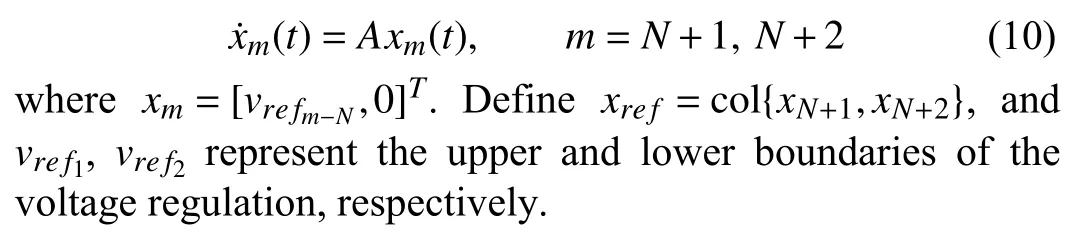
III.PROBLEM STATEMENT

Assumption 1: The communication topology between the PCC terminals of the sub-MG is directed.At least one virtual leader’s dynamics is directed to all sub-MG’s PCC terminals.
Assumption 1 is the basic standard assumption of MASs containment control.
In this paper, the faults are modeled as follows:
1) The communication links faults:
2) The sensors faults:
wherehiis the unknown sensor fault.
Assumption 2: The communication link faults,i=1,2,...,N,j=1,2,...,N+2, and their derivatives are bounded but unknown.The signs ofa¯i jare the same to those ofai j,respectively.
Assumption 3: The time derivative of sensor fault is bounded, i.e.,
Remark 2: An MG includes multiple power sources, actuators, sensors, and communication networks.Actuator faults can adversely affect the stability and performance of the MG.These faults can result in erroneous decision making and operation, impacting the effectiveness of the MG’s energy management and overall operation.Sensor faults can lead to inaccurate sensing and collection of environmental and energy data within the MG.This, in turn, affects the system’s dispatch and control strategy.Furthermore, communication among DGs in the MG occurs wirelessly and is susceptible to physical changes in the communication channel, noise interference from other sources, or malicious manipulation by hostile nodes.In this paper, we focus on sensor and communication fault issues.Assumption 2 guarantees the boundedness of the considered communication link faults and their derivatives, found in [30].Assumption 3 ensures the boundedness of the sensor derivatives, found in [18].

Then, L (t) is defined as


The dynamic model of theith agent is
Remark 3: The reference-based state observer in [30] is unavailable due to thexifull-state unmeasurability and sensor fault issues.Moreover, the boundaries of the fault-related parameters of the directed communication network and the communication and sensors are unknown.Therefore, we next design a new adaptive follower-based observer to handle communication and sensor faults.
IV.MAIN RESULT
The purpose of this section is to co-regulate the PCC voltagevbdi,i=1,2,...,Nin an MMS to a given region.Besides,from the practical needs of the power system, the proposed secondary control protocol does not depend on the global information of the directed communication network and the boundary of the fault factor.We design a containment-based secondary voltage strategy for communication link and sensor faults for a MMS, as shown in Fig.2.For simplicity, only one DG is shown in each sub-MG.
where

Let the observer controlleriin (17) be
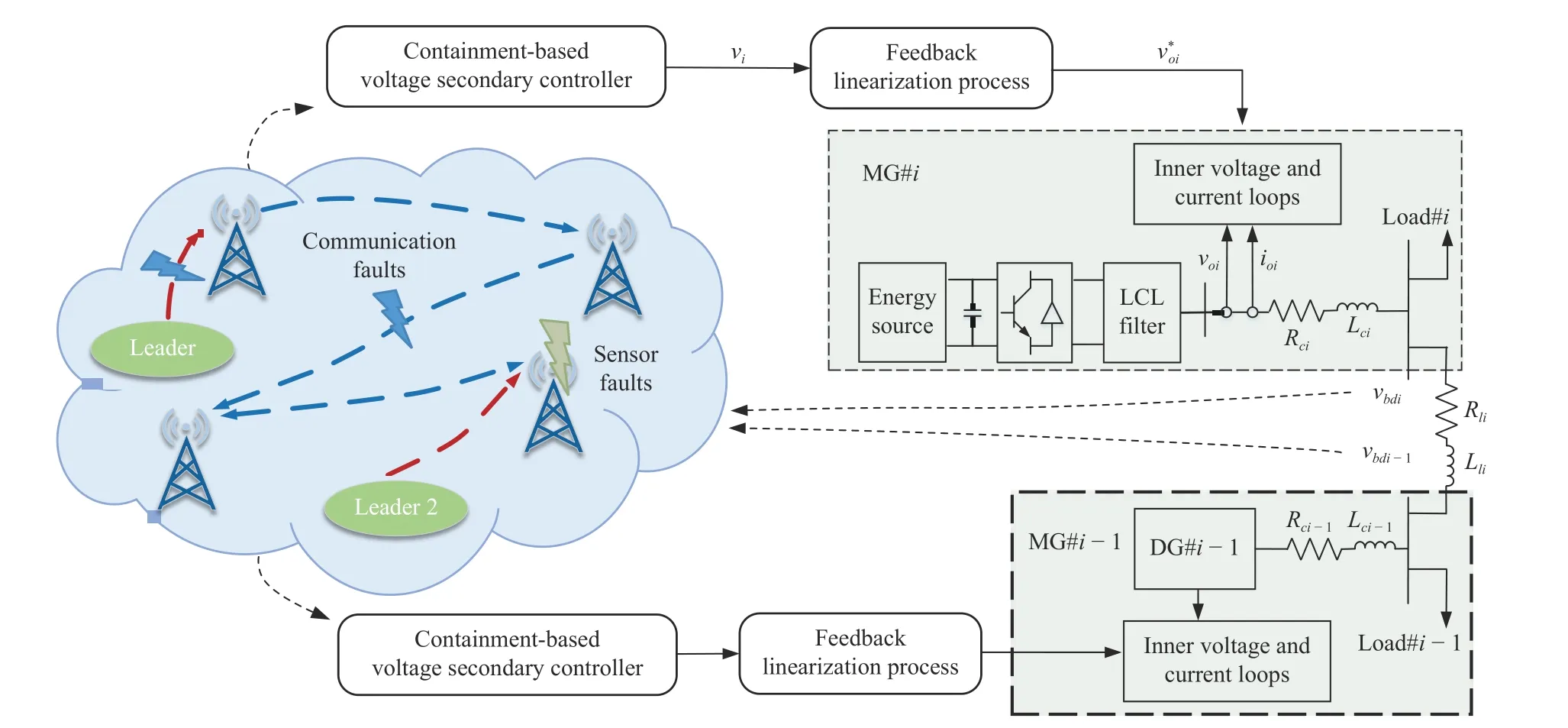
Fig.2.Block diagram of an MMS and the proposed containment-based secondary voltage regulation strategy for communication link and sensor faults.
where

Define ϵ =col{ϵ1(t),ϵ2(t),...,ϵN(t)}, then

Remark 4: It can be seen from Fig.2 that power cannot flow between DGs if the PCC voltagesvbdi,i=1,2,...,Nare controlled at their nominal value.Therefore, this paper introduces the control objective of containment control.On this basis, a secondary voltage regulation strategy based on containment control is proposed.The strategy limits each PCC voltagevbdito a reasonable range while having a voltage difference between sub-MGs to allow power flow.
Then,


It is easy to obtain
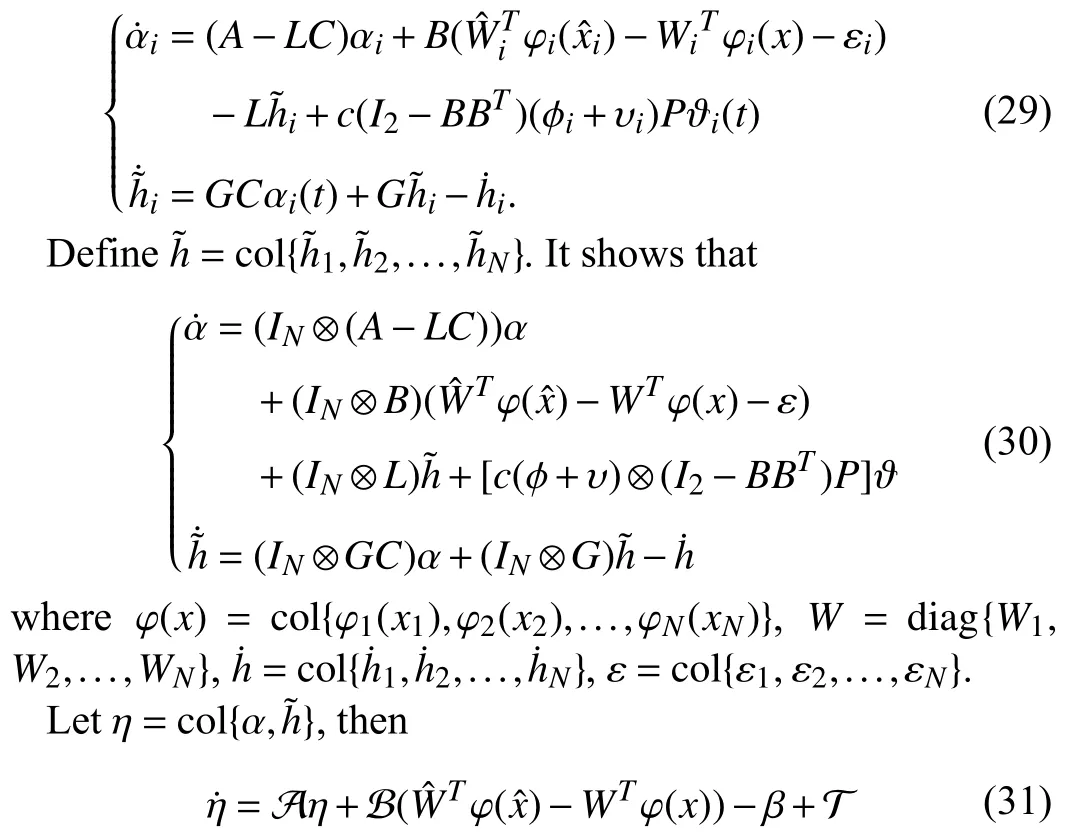
where
Theorem 1: Suppose Assumptions 1-3 hold, and there exist appropriate χm,m=1,2,3,4,5,11,12.P>0, Γ >0, M >0,R,GandLare with appropriate dimensions such that
where
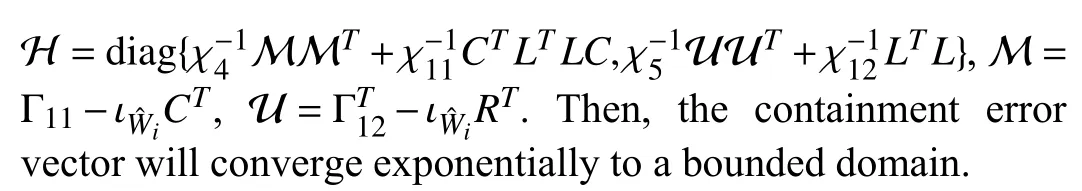
Proof: Consider the following Lyapunov function candidate:
where

Taking the derivative ofV1, from (26) and (31), we obtain that
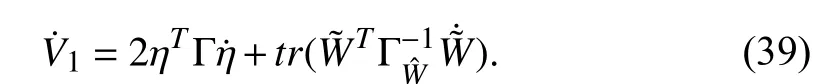

and
Applying (41)-(45) to (40), for any positive constants χ6and χ7, one can obtain that
Then,
Next, taking the derivative ofV2, from (20) and (21), we obtain that
Then,
From (23) and (24), we obtain //ϵ//≤//(t)////ϑ//.Define Kmas the lower bound of K(t).For any positive constant χ8,we obtain
By Lemma 2, the minimum eigenvalue of N(t) is denoted by λ0, it follows:

Moreover, for any positive constants χ11and χ12, it is easy to get
and
Sincesi>0 is sufficiently large such thatsi≥maxi=1,2,...,N{ki}holds, we obtain
It follows from (48)-(57) that (49) satisfies:

and
Furthermore,
Then,
where

Thereforeη,,ϑ,ϕandϑcan converge exponentially to the following bounded set:
Remark 5: In this paper, communication faults parameters are usually time-varying.When using the Lyapunov method,the derivatives of the parameters associated with the Laplace matrix must be introduced.Therefore, matrixBis not required in the observer controlleruˆiand its adaptive rate ϕidesign.
Remark 6: Designing adaptive output feedback tracking protocols is more challenging due to the asymmetric Laplacian matrix of the directed graph.The adaptive gain ϕiis used to estimate the eigenvalue information of the asymmetric Laplacian matrix associated with the directed graph.If the existing methods in [27] and [31] are used, the adaptive parameter ϕiis updated by ϕi=(t)PBBT Pϑi(t).It is easy to see the parameter ϕiwill increase monotonically.To avoid this phenomenon, a σ-modification technique is introduced in(20).
Remark 7: We introduce dynamic coupling gains ϕiandυito avoid global information and information related to the fault parameters.These gains are updated in dependence on the relative error ϑi(t).
V.SIMULATION RESULTS
This section aims to demonstrate the feasibility and effectiveness of the proposed resilient PCC voltage regulation strategy based on containment and output feedback and the resilience of the strategy under communication faults and sensor faults.For this purpose, we have simulated in the MATLAB/Simulink software environment for the MG shown in Fig.3.The MMS is tested with a combination of four sub-MGs.For simplicity, each sub-MG consists of only one DG.Table I provides the parameters of DGs, lines and loads in Fig.3.It is assumed that the DGs communicate with each other through the directed topology shown in Fig.4.DG#1,DG#4 receive information fromvref1,vref2, respectively.Then, after calculation, it is possible to obtainx¯=col{222.8571,211.4286,228.5714,234.2857}.

Fig.3.The example MG test system.
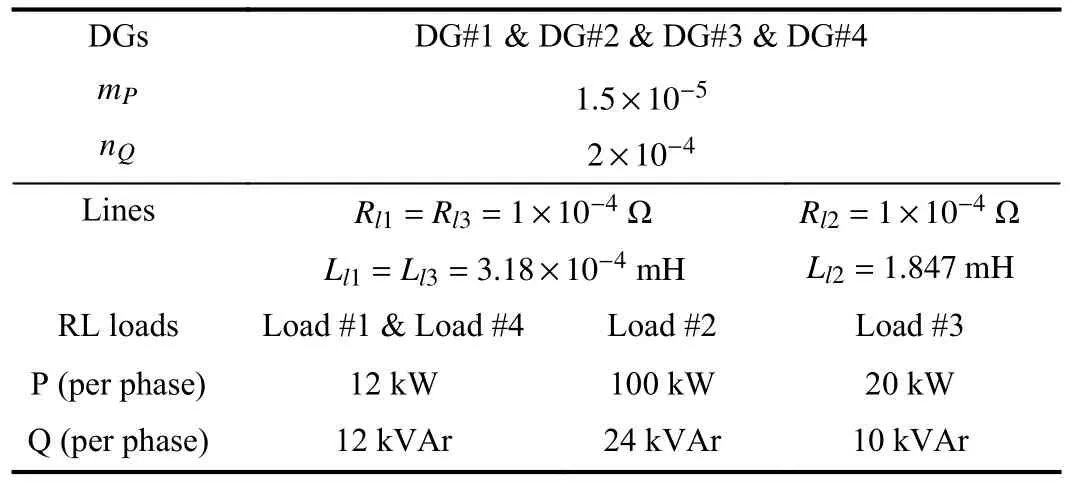
TABLE I SPECIFICATIONS OF THE MG TEST SYSTEM
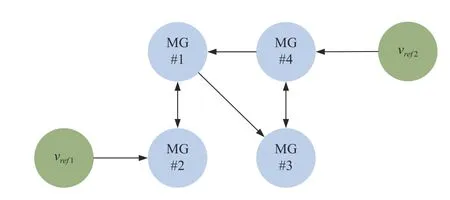
Fig.4.The considered communication structure.
This case scenario examines the capability of the proposed resilient voltage regulation approach after islanding att=0.0 s.For this purpose, the following four test scenarios were performed:
1) Att=0.4 s, the containment-based PCC voltage regulation secondary control cuts in.
2) Att=0.7 s, MG #4 was disconnected.
3) Att=1 s, MG #4 was reconnected.
4) Att=1.3 s, load # 1 cuts off 5 0%.
5) Att=1.6 s, 50% of load #1 is restored to its original value.
Solving (33) gives a solution

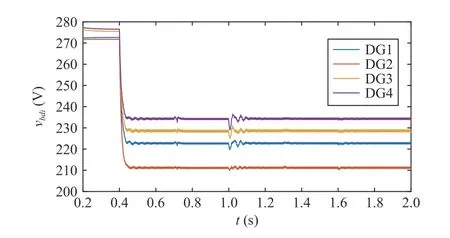
Fig.5.The PCC voltages , i =1,2,...,4.
To verify the effectiveness of the containment-based PCC regulation algorithm in an MMS, the algorithm initially relies on only primary control to maintain voltage stability by adjusting the droop factor.As shown in Fig.5, the primary control successfully achieves voltage stability and provides a timely response.However, operation in differential mode causes the voltage to deviate from the nominal value.Therefore, introducing a designed regulation control layer is crucial for the cooperative regulation of PCC voltages in an MMS.After the secondary control algorithm is activated whent=0.4 s, it is observed that the PCC voltages are regulated into a convex packet formed by reference valuesvref1,vref2,thus, the voltage is restored within a reasonable range while a voltage difference exists between the PCC voltages to achieve the power flow between the MGs.Att=0.7 s andt=1.0 s,the PCC voltages fluctuate due to the separation and subsequent reconnection of the sub-MGs.The voltage quickly returns to its original value, indicating that the regulation strategy effectively maintains voltage stability.Similarly, att=1.3 s andt=1.6 s, the proposed PCC voltage regulation strategy effectively restores the desired voltage level after the load is temporarily disconnected and converted.In addition,Figs.6-9 indicate the corresponding output voltage, controller, and active and reactive power changes, further illustrating the effectiveness of the voltage regulation proposed in this paper.

Fig.6.Output terminal voltage, i =1,2,...,4.

Fig.7.The controllers , i =1,2,...,4.
In summary, the effectiveness of the containment-based PCC voltage regulation strategy proposed in this study is verified under load shifting and plugging scenarios, providing a reliable means to ensure the stable operation of the MG system.

Fig.8.The active power Pi, i =1,2,...,4.

Fig.9.The reactive power Qi, i =1,2,...,4.
VI.CONCLUSIONS
This paper has proposed a containment-based AC MG secondary control strategy to regulate the PCC voltage.Unlike previous voltage regulation strategies, the applied feedback linearization transforms the PCC voltage regulation control into a distributed output feedback tracking problem of a linear MAS with nonlinear dynamics.If multiple PCC voltages are set to return to the reference voltage collectively, it will not be possible to perform power flow between sub-MGs.Therefore,the idea of containment control is introduced.The control objective is to restore to a reasonable range while there is a voltage difference between PCC voltages.In addition, network communication between DGs and sensor failures in DGs are unavoidable.A novel resilient fault-tolerant control algorithm with output feedback based on state observer has proposed to achieve communication resilience while avoiding the effects of sensor failures.At the same time, it avoids the global information of the directed communication network and fault parameters related to applications.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Multi-Objective Optimization for an Industrial Grinding and Classification Process Based on PBM and RSM
- GraphCA: Learning From Graph Counterfactual Augmentation for Knowledge Tracing
- Adaptive Graph Embedding With Consistency and Specificity for Domain Adaptation
- The ChatGPT After: Building Knowledge Factories for Knowledge Workers with Knowledge Automation
- An Optimal Control-Based Distributed Reinforcement Learning Framework for A Class of Non-Convex Objective Functionals of the Multi-Agent Network
- Can Digital Intelligence and Cyber-Physical-Social Systems Achieve Global Food Security and Sustainability?
