Lagrange插值对相渗曲线归一化方法的改进——以M油田相渗曲线为例

路 强,任宜伟,尹彦君,张 震,王中华,陈秋月

(中海油能源发展股份有限公司工程技术分公司,天津 300457)

相对渗透率指岩石孔隙中饱和多相流体时,岩石对每一相流体的有效渗透率与岩石绝对渗透率的比值。油水相对渗透率与含水饱和度的关系曲线称为相对渗透率曲线[1],即相渗曲线。该曲线是研究储层多相流动的重要参数,是油田开发动态分析、开发方案设计、油藏数值模拟等工作的基础资料[2]。油藏开采初期,实验室需要测定多条相对渗透率曲线,为了获得一条能够准确反映储层流体渗流特征的相对渗透率曲线,需要对相对渗透率曲线进行必要的插值,以得到一条归一化的曲线。对于不同类型的相渗曲线应该如何进行插值计算,针对这一问题,本文剖析了Lagrange插值对相渗曲线归一化的改进。

1 相渗曲线的分类

不同储层的油相相渗曲线变化趋势基本一致,表现为一条光滑的单调递减曲线,而水相相渗曲线则差异较大,王国先[3]按照水相相渗曲线形态将相渗曲线分为五类,中高渗储层常见的是水相上凹型(图1a),低渗储层常见的是水相上凹型和水相直线型(图1b),低渗敏感性储层常见的是水相下凹型(图1c)和水相上凸型(图1d),低渗裂缝型储层主要是水相靠椅型(图1e)。

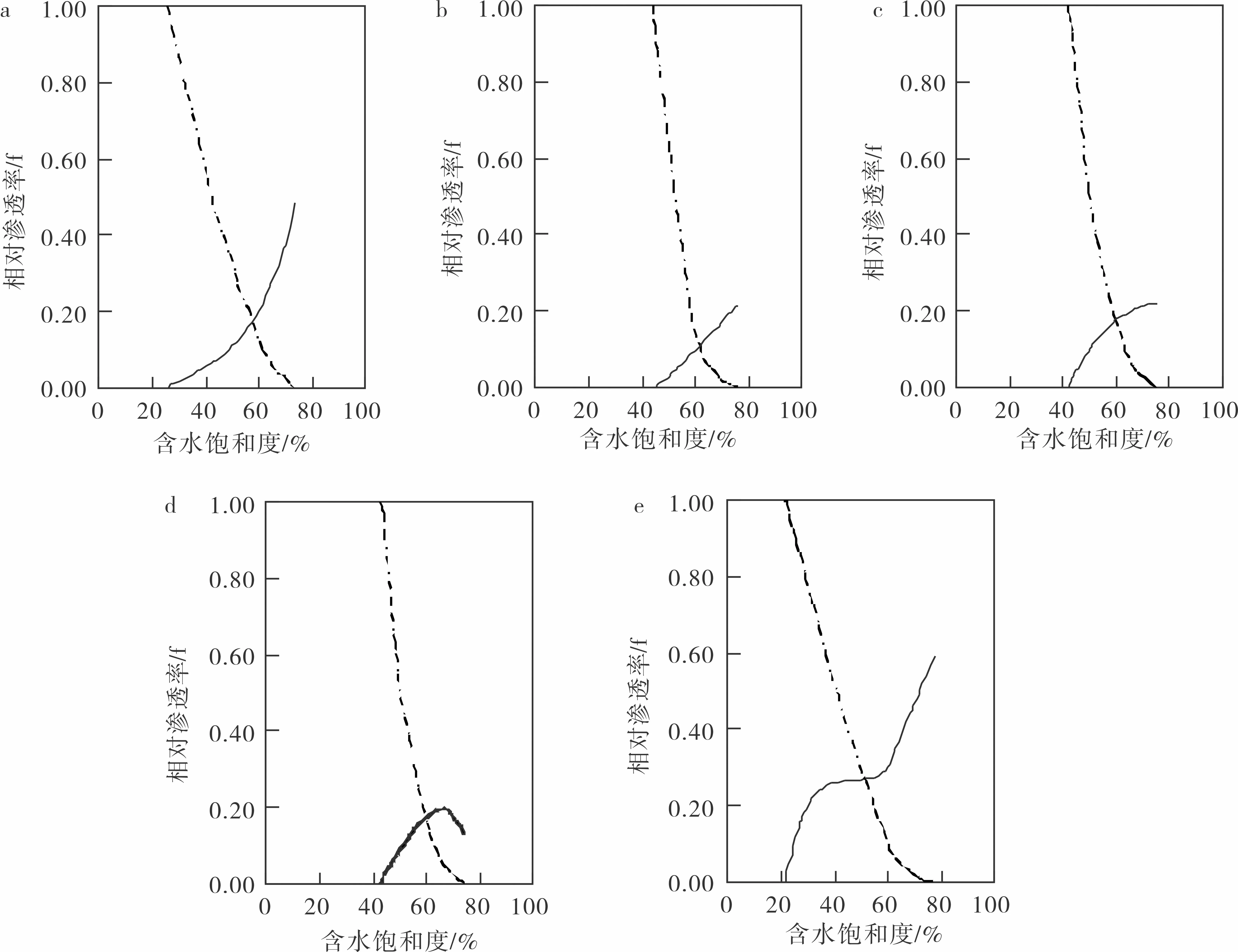
图1 不同类型相渗曲线

水相上凹型:实验室测得的相渗曲线绝大多数都是水相上凹型,这类曲线为标准型油水相对渗透率曲线。随含水饱和度增加,水相曲线光滑、无拐点、单调递增,曲线近三次多项式。

水相直线型:曲线形态与水相上凹型曲线相似,也较为常见,受储层孔隙填充物膨胀影响,曲线不上凹,随含水饱和度增加,水相曲线光滑、无拐点、单调递增,曲线近一次多项式。

水相下凹型:曲线反映出储层黏土矿物含量高且已发生盐(水)敏,黏土矿物遇水膨胀堵塞喉道,水相流动阻力增大,随含水饱和度增加,水相曲线光滑、无拐点、单调递增,曲线近二次多项式。

水相上凸型:水相上凸型的水相曲线与水相下凹型曲线相似,但尾部明显下掉,曲线形态近似驼峰,随含水饱和度增加,水相曲线光滑、一个拐点,曲线近二次多项式。

水相靠椅型:裂缝较发育储层的相渗曲线多表现为水相靠椅型,随含水饱和度增加,水相曲线光滑、两个拐点,曲线近三次多项式。

由于一次多项式和二次多项式是三次多项式的特殊形式,因此,五类相渗曲线的水相曲线形态均与三次多项式曲线近似。

2 相渗归一化处理方法及改进

相渗归一化处理有三种方法:平均法、经验公式法[4-8]、相对渗透率特征曲线法[9]。平均法是相渗曲线归一化处理的一种常用方法,该方法不需要对实验数据进行拟合,能最大程度地保存原始相渗曲线的形态,但是潘婷婷[10]认为该方法精度低且曲线不光滑。

2.1 平均法

平均法包括平均相对渗透率法和平均饱和度法[11],两种处理方法类似,处理过程如下:

1)选取具有代表性的油水相对渗透率曲线数据;

2)对各岩心样品的实验数据进行无因次化处理(式1),并绘制无因次后的油水相对渗透率曲线;

(1)

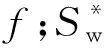
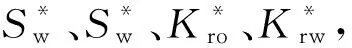
(2)

4)将各样品的相渗曲线特征值分别进行算术平均(式3),并将平均值作为平均相渗曲线的特征值;

(3)

5)将求得的平均无因次相对渗透率曲线换算成无因次化之前的相渗曲线,其公式为:

(4)

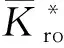
2.2 平均法的改进

Lagrange插值法原理是:在插值点的附近选取若干合适的结点,构造一个简单的插值函数y=L(x),要求L(x)穿过选取的结点。在所选数据区间用L(x)作为原函数f(x)的值,使得f(xi)=L(xi)(i=0,1,…,n-1)成立[16]。

1)构建Lagrange插值基函数。给定n个结点xi(i=0,1,…,n-1)上的函数值yi=f(x),则插值基函数的表达式为:

(5)

基函数满足lj(xj)=1,lj(xi)=0(i≠j)。

2)n个结点构建的Lagrange多项式L(x),其表达式为:

(6)

其特点是满足L(xi)=yi(i=0,1,…,n-1)。

2.3 Lagrange插值法的改进及实现

郑洪印[17]1993年提出利用Lagrange插值法进行插值,插值时选取距离插值点最近的三个相邻结点进行Lagrange插值,但该方法存在以下问题:三个插值结点构造成二次多项式,如果多项式对称轴介于三个插值结点之间,曲线会出现拐点。

一般情况下,插值结点越多,预测结果越准确,但插值次数越多,越容易出现龙格现象。五类相渗曲线的形态均与三次多项式曲线近似,4个结点可以确定唯一的三次多项式,因此在n个结点中选取距离插值点最近的4个结点进行插值,且使指定插值点t位于4个结点之间。

3 实例分析

以M油田相渗曲线为例,实验室共测得四块岩心的相渗曲线数据(表1),每块岩心选取三个实验数据点作为盲点,对比线性插值法、四点Lagrange插值法、三点Lagrange插值法的精度。

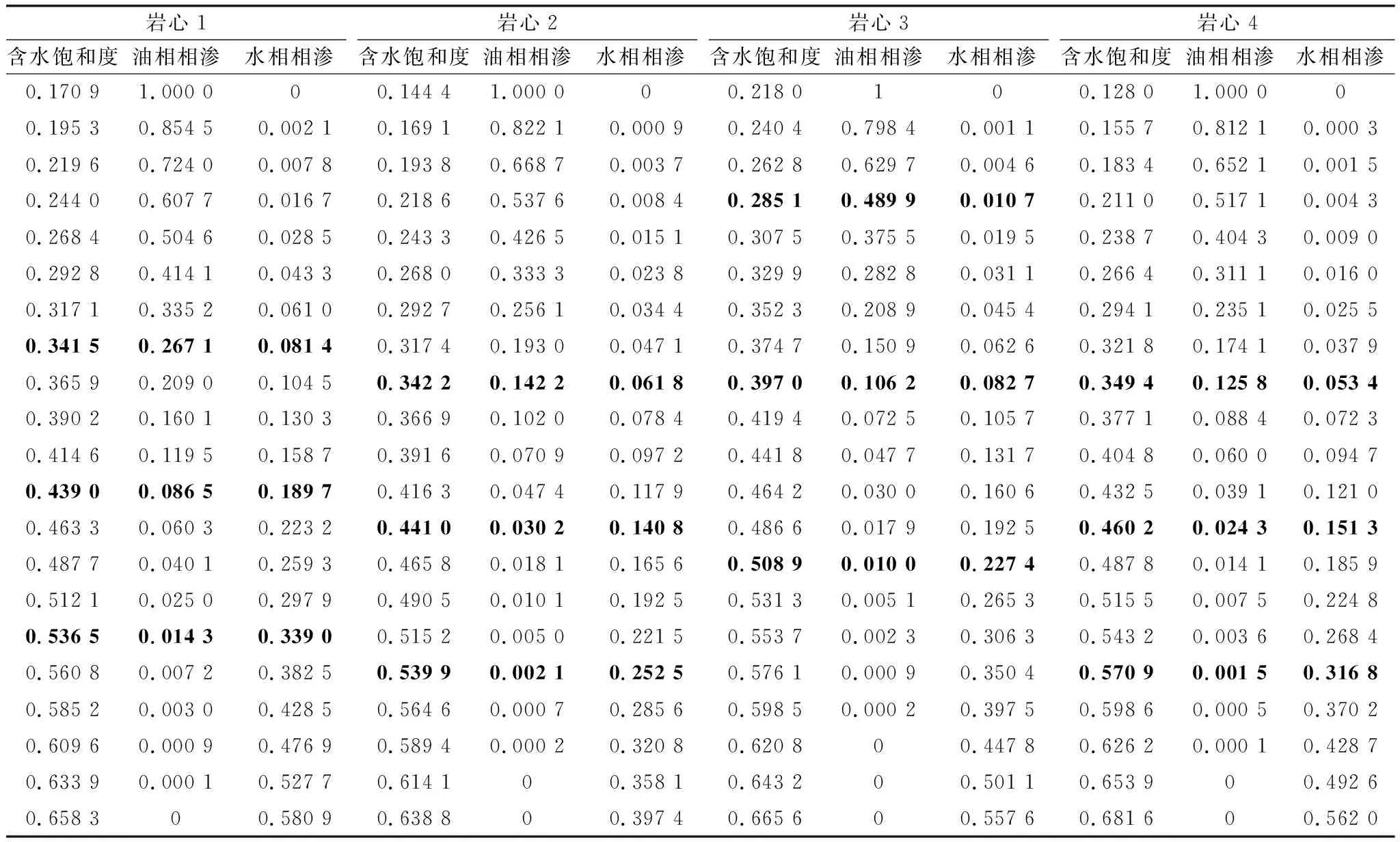
表1 H油田岩心相渗曲线数据

结果表明:线性插值法盲点最高相对误差可达40%,油相相对渗透率平均误差为6.13%～17.95%,水相相对渗透率平均误差为0.88%～4.83%;三点Lagrange插值法盲点最高相对误差为13.33%,油相相对渗透率平均误差为0.83%～4.99%,水相相对渗透率平均误差为0～0.1%;四点Lagrange插值法盲点最高相对误差为0.41%,油相相对渗透率平均误差为0～0.14%,水相相对渗透率平均误差为0～0.09%(表2)。因此,Lagrange插值法的精度明显高于线性插值法,而四点Lagrange插值法精度高于三点Lagrange插值法。

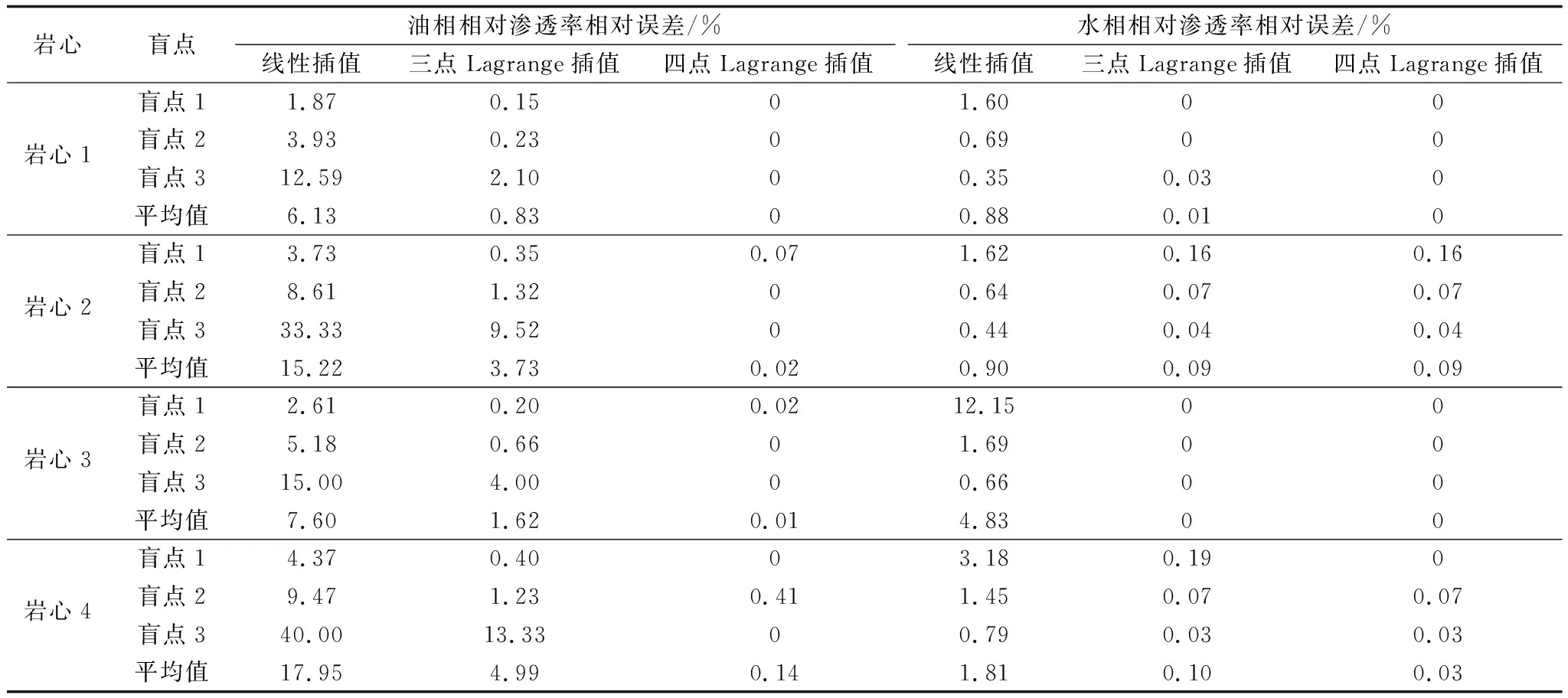
表2 不同插值法相对误差对比

4 结论

1)五类典型相渗曲线形态与三次多项式曲线形态类似,Lagrange插值法可以构建一个多项式,保证实验数据点误差为零,并且能够最大程度保持每一类相渗曲线的形态。

2)采用线性插值法的相对误差最高,而Lagrange插值法的相对误差较小。相较于三点Lagrange插值法,四点Lagrange插值法构造的曲线为三次多项式,曲线形态更符合五类相渗曲线的形态,计算精度更高。