出入立体库的环形有轨穿梭车布局设计与优化
2023-10-20张之臻林树茂
张之臻 林树茂
1 北京起重运输机械设计研究院有限公司 北京 100007 2 北京市自动化物流装备工程技术研究中心 北京 100007
3 机械工业物料搬运工程技术研究中心 北京 100007
1 研究背景
近年来,随着我国大力发展推广智能化制造产业的发展[1],尤其是在自动化工业领域的自动化立体仓库发展格外迅速。自动化仓储是一种自动化、密集化的物流存储系统,该系统集高密度立体货架、堆垛机、输送机、环形有轨穿梭车(Rail Guided Vehicle,以下简称环形车RGV)及软件调度系统为一体[2]。当货物在出入自动化立体仓库前,需要由环形车RGV-输送线协同作业才能完成将货物运输至出入库堆垛机输送线,进而完成货物的出入库操作[3]。一般情况下,业主方会梳理业务流,结合目前业务的发展预估未来市场需求的变动,待项目立项后再通过内部论证或请咨询公司进行项目的可行性研究,在初步设计阶段合理梳理出未来立体库的货物规格尺寸、建筑尺寸、效率需求及投资估算等需求[4]。相关业务设计者需考虑能力匹配、能力均衡、经济性、冗余、安全性[5]等原则,结合项目现场的客观条件对环形车RGV-输送线布局设计及优化方案进行规划,供业主决策方比对分析。相对于传统模式的单一环形车RGV,在环线中增加缓存输送线是近年来的主要优化方式,可增加缓存线在经济性和带来效率的提升比例确实有待考量,且在布局设计过程中考量的因素较多,仅凭借经验指导实践是非常困难的,且得出的规划布局未必是真实的系统最优解。因此,建立基于实际情况的数学模型并求解非常有必要,能够帮助决策者快速得出具有参考价值的布局比对分析解,可有效减少出入库作业总时间,提高仓储作业整体效率,为自动化仓储出入库区布局与优化提供了理论支持和方法借鉴。
2 自动化立体堆垛机库出入库系统特点
1)多目标性 自动化立体仓库的出入库作业需要权衡出入库流量、各环形车RGV的效率、出库交付和入库作业的时间要求等多个目标。
2)协同性 在自动化立体堆垛机仓储系统中,每个货道都有堆垛机,货物的出入库作业需要堆垛机-输送机、环形车RGV-输送机对接后协同完成。在出库作业时,堆垛机将待出库货物从相应库位取出并放置于出库输送机,环形车RGV与输送机对接,接取货物并运输至出库口的输送机上;环形车RGV将货物由入库输送机处提取,携货物运输至对应巷道口将货物放置于入库输送机,再由堆垛机将货物运输至具体货位。
3)复杂约束 自动化立体仓库出入库系统受很多复杂约束限制,其中采用环形车RGV完成出入库作业调度时,约束包含但不局限于受待出入库货物的货位分布、小车当前状态、多辆小车路径拥堵及碰撞等约束的影响。
4)动态性 小车故障、多车拥堵、紧急出入库任务的插入都会加大出入库作业的困难程度,造成出入库系统的动态性。
因此,环形车RGV-输送机组成的出入库系统的合理化规划与设计优化对减少出入库作业总时间、提高了仓储作业整体效率具有重大意义。
3 模型建立
本文以由环形车RGV-堆垛机输送机组成的出入库系统为研究对象,通过对比方案同在环形车RGV中增加输送机的方案,分别构建函数对环形车RGV-堆垛机输送机系统的总成本进行测度,构建了整数随机规划模型,并以基于抽样平均近似算法对问题进行求解。
3.1 假设条件
1)自动化立体仓库区巷道均为单伸巷道,所有巷道宽度均一致;
2)自动化立体仓库区域库位数足够且满足需求的储位数,货物均匀分布在各个巷道,立体仓库的出入库口均在有输送机的一侧,假设各巷道的出入库作业独立且均匀分布,各巷道堆垛机的复合作业效率一致;
3)假设出入库效率各为总系统效率的一半;
4)假设环形车RGV在弯道处平均速度恒定,环形车在系统中仅一辆;
5)环形车RGV在转弯前后的直线段加速度a,直线段初始速度和最终速度均为0,且全程速度均未达速度上限, 环形车RGV在直线段的运行轨迹如图1 所示,运行时间t和总运输距离S、加速度a之间的关系为
6)出入库口输送机自环形车RGV直线段中间开始均匀对称排布,数量一致;
7)增加内部输送线时,仅增加一组出入缓存输送线,新增输送线的出入口同系统出入货口、堆垛机立体库输送机出入货输送机口对应;
8)增加内部输送线时,若货物同时可走环线RGV和出入缓存输送线时,优先走出入缓存输送线。
3.2 自变量、参数定义、决策变量
1)自变量定义
本文建模中的自变量有:i为货物经环形车RGV-输送机堆垛机进入自动化立体库的第i个巷道入库,i∈[1,n1];j为货物经堆垛机输送机-环形车RGV 运出自动化立体库的第j个巷道出库,j∈[1,n1];k为货物经入库输送机-环形车RGV的第k个入库口进入运输系统,k∈[1,n2];u为货物经环形车RGV-出库输送机的第u个出库口运出运输系统,u∈[1,n2]。
2)参数定义
本文建模中的参数有:n1为单深位堆垛机货架系统数量,其中n1={1,2,3,4,…};n2为出库口数量或入库口数量,其中n2={1,2,3,4,…};a为环形车RGV在转弯后进入直线段的加速度;W为单深位堆垛机货架的宽度;L为环形车RGV直线段的长度;R为环形车RGV弯道半径;vCircle为环形车RGV 在弯道处的平均速度;TTask为完成一次环形车RGV 与输送机或输送机与环形车RGV交接工作所用的时间;EStoraging为系统入库效率;ERetrievalling为系统出库效率;EStorage为堆垛机货架系统单一堆垛机的复合作业效率;EInput为单一入货口输送机效率;EOutput为单一出货口输送机效率;Xijku为在具体情景下单次作业的出库或入库量。
3)决策变量
本文建模中的决策变量有:TCircle为环形车RGV 完成一次弯道行径所用的时间;Tij为环形车RGV在输送机-堆垛机段的运行总时间,入库货物经环形车RGV-输送机堆垛机进入自动化立体库的第i个巷道入库,出库货物经堆垛机输送机-环形车RGV运出自动化立体库的第j个巷道出库;Tku为环形车RGV在入库输送机-出库输送机间直线段的运行总时间,入库货物经入库输送机-环形车RGV的第k个入库口进入运输系统,出库货物经环形车RGV-出库输送机的第u个出库口运出运输系统;T2ijku为在具体情景下环形车RGV-输送机系统中间增加输送线,以提高系统出入库效率,加快完成出入库作业的总时间;T1为由环形车RGV-输送机系统完成出入库作业的总时间;T2为由增加输送线-环形车RGV-输送机系统完成出入库作业的总时间;T为由环形车RGV-输送机系统完成出入库作业的总时间。
3.3 模型构建
环形车RGV直线段长度L约束可表示为
为满足自动化立体仓库堆垛机系统的出入库要求,所需要配置的巷道数量约束,且n1为正整数,其中为向上取整函数,约束可表示为
为满足环形RGV-输送机出入库系统的要求,且出入库效率各为系统总体效率的一半,n2为正整数,其中为向上取整函数,所需要配置的出入库口数量约束条件可表示为
根据式(2)、式(3),可推导出单深位堆垛机货架系统数量n1和出库口数量或入库口数量n2间的关系,其中为向上取整函数,具体可表示为
根据假设环形车RGV 在弯道处作匀速运动, 则TCircle可表示为
环形车RGV 直线段的长度与堆垛机货架系统宽度间关系约束可表示为
3.3.1 环形车RGV-输送机模型构建
如图2 所示,拆解环形车RGV-输送机模型,合理化分解问题,将环形车RGV的运行轨迹划分为环形车RGV与输送机-堆垛机段、环形车RGV与出入库输送机段、环形车RGV弯道段作为分析研究对象。

图2 环形车RGV-输送机示意图
1)环形车RGV与输送机-堆垛机段
环形车RGV与输送机-堆垛机段的运行总时间为Tij,包含入库货物经环形车RGV-输送机堆垛机进入自动化立体库的第i个巷道入库的时间和出库货物经堆垛机输送机-环形车RGV运出自动化立体库的第j个巷道出库的时间,其中i∈[1,n1],j∈[1,n1],Tij形成一个i·j的矩阵,具体可表示为
当i<j时,有
当i=j时,有
当i>j时,有
由此,Tij可表示为
2)环形车RGV与出入库输送机段
环形车RGV在入库输送机-出库输送机间直线段的运行总时间,入库货物经入库输送机-环形车RGV的第k个入库口进入运输系统,出库货物经环形车RGV-出库输送机的第u个出库口运出运输系统, 其中k∈[1,n2]、u∈[1,n2]、Tku形成一个k·u的矩阵,具体可表示为
其中,无论k和u的关系如何,每一个Tku的表达式均成立,即
3)环形车RGV弯道段
根据式(5),环形车RGV在弯道处作业总时间可表示为
在此情景下,Xijku=2,以环形车RGV-输送机系统总时间T1为目标构建函数,得到其表达式为
3.3.2 环形车RGV -输送机-增加内部输送线模型构建
如图3 所示,当增加内部输送线时,根据假设仅增加1 组出入缓存输送线,其长度为2R,位置设置在环形车RGV最中间的出入货口输送机对应处,此时缓存输送线与出入库输送机-堆垛机相应出入库输送机存在对应关系。

图3 环形车RGV-输送机-增加内部输送线示意图
1)在环形车RGV-输送机系统中间增加缓存输送线,从入库口输送线k看,第1 次放在入库缓存线的入库货物k1=1 时,第2 次RGV携带的入库货物k2∈[1,2,3,…,n2]可利用入库缓存线,此时要求环形车RGV-输送机堆垛机系统的i2≤n1/2 ≤i1,即可利用新增入库缓存线,此时Xijku=3。
2)在环形车RGV-输送机系统中间增加缓存输送线,从出库堆垛机-输送线j看,要求第1 次放在出库缓存线的出库货物j1≤n1/2 时,第2 次RGV携带的出库货物n1/2 ≤j2≤n1可利用出库缓存线,此时要求环形车RGV-输送机系统的u2≤u1≤n2,即可利用新增的出库缓存线,Xijku=3。
3)基于上述2 种情况,当且仅当k1=1 ≤k2≤n2、i2≤i1=n1/2、n1/2 =j1≤j2≤n1、u2≤u1≤n2时,新增的出入库缓存线均可被充分利用,此时Xijku=4。
4)除上述情况,其他事件的概率同环形车RGV-输送机模型情况,此时Xijku=2。
由以上分析可得,T2ijku和T2的表达式为
将环形车RGV-输送机模型与环形车RGV-输送机-增加内部输送线模型进行对比分析,以完成出入库作业总时间最少为目标构建函数,表达式为
3.4 基于抽样平均近似算法的模型求解方法
随着算例中堆垛机巷道数目、出入库口数目的增加,情景数量也将呈指数增加,很难在短时间内求解该问题并得到大量问题的精确解法,故应采用抽样平均近似算法对问题进行求解。该方法对于解决此类问题,尤其是数量较大的随机情景的混合整数随机规划问题有较好效果,其能在确保求解精度的前提下大幅缩短求解时间。该算法的具体求解过程如图4 所示。
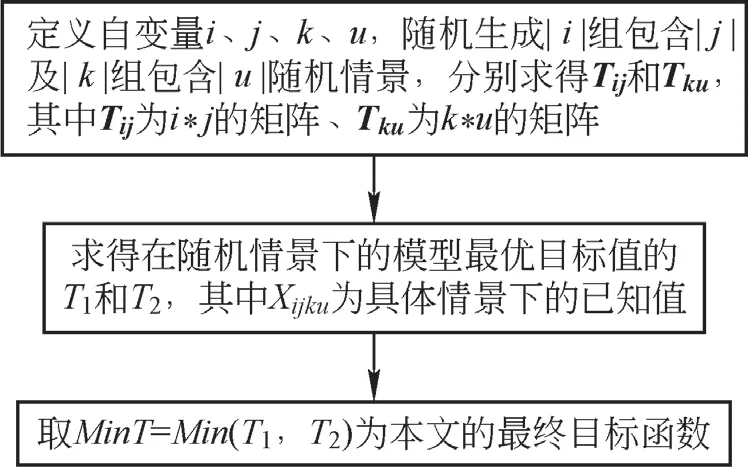
图4 基于抽样平均近似算法的模型求解过程
4 项目案例验证
以某自动化立体仓库的出入库环形车RGV-输送机系统为例,根据企业实际运营情况,环形车RGV-输送机模型和环形车RGV-输送机-增加内部输送线模型分别如下图5 和图6 所示,出入库系统的相关效率如表1所示。

表1 系统效率相关参数 托/s

图5 环形车RGV-输送机模型案例图
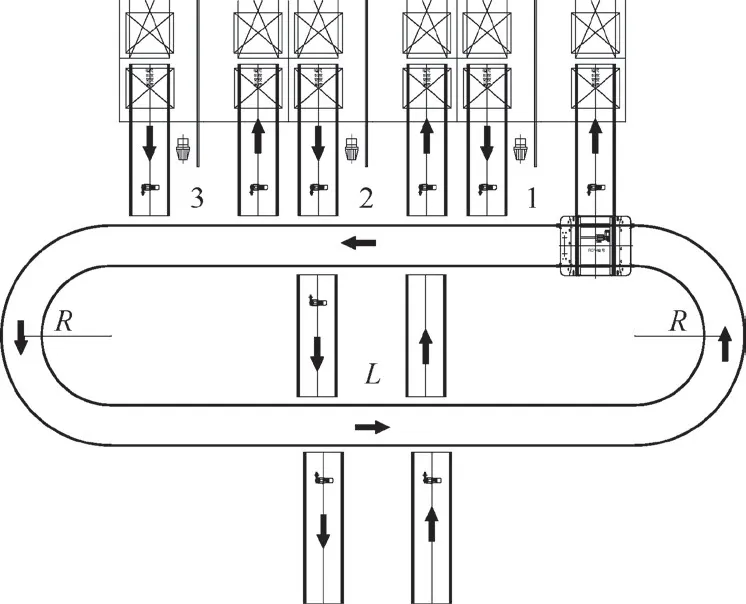
图6 环形车RGV-输送机-增加内部输送线模型案例图
根据式(4)可推理得到n1/n2=3/1 =3,上述实际情况符合公式推理。其他参数情况为:环形车RGV在转弯后进入直线段的加速度a=1/3 m/s2,单深位堆垛机货架的宽度W=4.2 m,环形车RGV直线段的长度L=12 m,环形车RGV 弯道半径R=1.5 m,环形车RGV在弯道处的平均速度vCircle=1/3 m/s,完成一次环形车RGV与输送机交接工作所用时间TTask=8 s。
4.1 环形车RGV-输送机系统求解
对环形车RGV-输送机模型进行拆解,将问题合理化分解,将环形车RGV的运行轨迹划分为环形车RGV与输送机-堆垛机段、环形车RGV与出入库输送机段、环形车RGV弯道段等3 段进行分析。
1)环形车RGV与输送机-堆垛机段
根据式(11)可推理Tij的表达式为
2)环形车RGV与出入库输送机段
环形车RGV在入库输送机-出库输送机间直线段的运行总时间Tku可根据式(12)推理得出,其表达式为
3)环形车RGV弯道段
根据式(14)可得环形车RGV在弯道处作业总时间为
由此,以环形车RGV-输送机系统总时间T1为目标构建函数,表达式为
4.2 环形车RGV -输送机-增加内部输送线系统求解
当增加内部输送线时,根据假设仅增加1 组出入缓存输送线,其长度为2R,位置设在环形车RGV中间部位的出入货口输送机对应处,此时缓存输送线与出入库输送机-堆垛机相应出入库输送机也存在对应关系,具体如图5 所示。
由于形车RGV中间部位的出入货口输送机仅1 组,则Tku=T11;在根据假设增加内部输送线时,若货物同时可以走环线RGV和出入缓存输送线,则优先走出入缓存输送线。
1)在环形车RGV-输送机系统中间增加缓存输送线,仅利用新增入库缓存线,即每次复合作业对于系统来说,完成2 个货物的入库和1 个货物的出库,Xijku=3。从堆垛机-入库输送线i来看,第1 次放在入库缓存线的入库货物i1=2 时,第2 次RGV携带的入库货物i2∈[1,2],完成1 次出库j=3。
2)在环形车RGV-输送机系统中间增加缓存输送线,仅利用新增出库缓存线,即每次复合作业对于系统来说,完成1 个货物的入库和2 个货物的出库,此时Xijku=3。从堆垛机-出库输送线 看,若第1 次放在出库缓存线的出库货物j1=1 时,要求i=1,则第2 次RGV携带的出库货物j2∈[2,3];若第1 次放在出库缓存线的出库货物j1=2 时,要求i∈[1,2],则第2 次RGV携带的出库货物j2∈[2,3]。
3)基于上述2 种情况,当且仅当i1=2、j1=2,且i2∈[1,2]、j2∈[2,3]时,新增的出入库缓存线均可被充分利用,此时Xijku=4。
4)除上述情况,其他事件的概率与环形车RGV-输送机模型的拆解相同,Xijku=2。
另外,同理可根据T2ijku得到T2,根据式(17)求解模型可知采用增加环线方式具有明显优势,求解得到的结果为T1=274 s、T2=231 s。
5 总结
本文考虑由环形车RGV -堆垛机输送机组成的出入库系统为研究对象,通过对比方案同在环形车RGV 中间部位增加输送机的方案,分别构建整数随机规划模型并对环形车RGV -堆垛机输送机系统总成本进行了测度,以基于抽样平均近似算法对问题进行求解,并基于实际案例对问题进行具象化分析,表明研究结果对实践具有指导意义。
为了更加贴近真实情况,采取更复杂的分布拟合出入库的实际情况;采取更多维度对目标函数进行约束,以更贴近于环形车RGV -输送机出入库系统运行情况;采取更为丰富的求解方法达成最优化问题求解。
