基于VOF-LPT模型的强旋来流条件横向射流破碎雾化特征研究*

2023-10-20谢名云濮天昊吴胜奇

应用数学和力学 2023年9期

谢名云, 濮天昊, 刘洪, 吴胜奇,2

(1. 上海交通大学航空航天学院, 上海 200240;2. 上海交通大学四川研究院, 成都 610500)

0 引言

液体垂直于来流方向喷射作为一种有效燃料喷注方式,已经被广泛应用于冲压发动机燃烧室以及加力燃烧室[1-2]．而在先进航发燃烧室中(如TAPS),旋流来流与射流的相互作用成为一种重要的燃料掺混模式．对旋流来流下射流破碎雾化特征的深入研究有利于理解随后的混合燃烧过程,进而优化设计以提高燃烧室燃烧效率,减小污染物排放[3]．

横向来流中液体射流的破碎机理对后续的液雾空间分布以及液滴粒径具有决定性作用,并且会影响发动机燃烧效率及燃烧稳定性,因而受到了大量学者的关注[4-6]．随着液体射流的喷出,液柱首先经历表面破碎,其中不断有液带或小液滴从液柱边缘剥离,液柱在来流气动力作用下变得扁平并发生偏转;沿着射流速度方向,迎风面不稳定性波不断生长,最后液柱在波谷处断裂进而发生柱状破碎,使液柱整体破碎成液块和大液滴．基于来流We数的大小可将射流的柱状破碎分为毛细破碎、袋状破碎、多模态破碎和剪切破碎[7],对于气动力作用较为显著的情况(大We数),柱状破碎通常认为是由迎风面KH不稳定性波的发展导致[8-9]．Sallam等[10]将边界层剥离理论应用于液柱的表面破碎过程,假设从液柱剥离后形成的液滴尺寸与边界层厚度成正比,提出了表面破碎后沿喷注方向变化的粒径公式．Behzad等[11]基于线性稳定性分析提出了无黏的射流表面破碎机理,认为剪切不稳定性伴随离心的RT不稳定性是液柱发生表面破碎的内在机理,并给出了方位剪切不稳定性出现的判据．此外,Broumand等[12]对横向射流破碎模态、喷注轨迹、破碎机理以及粒径模型等特征做了详细的综述,同时也指出旋流、湍流等非均匀来流与射流相互作用的机理需要进一步研究．

旋流与射流相互作用的研究主要集中在射流的喷注轨迹、油气空间分布特征等方面．Becker等[13]研究了在双旋来流条件下燃料空间分布与动量比的关系,提出了燃油喷注动量比应与气流相匹配以扩大燃料分布的区域．Freitag[14]在不同环境温度压力下研究了旋流来流下的喷雾雾化特征,结果发现高温高压条件下液滴Stokes数较小,喷雾轨迹与流场平均流线轨迹吻合较好;此外将Stokes数分为湍流和旋流导致的Stokes数,发现旋流Stokes数随密度比增大而增加．Sikroria等[15]讨论了不同旋流数下射流喷注轨迹及喷雾面积的变化趋势,旋流不仅能使液体急剧弯曲和分解,减小径向穿透,也增大了喷雾的扩散面积．Tambe等[16]发现:由于离心力和边界轴向速度的降低,喷注轨迹随旋流角度的增大而增加;并且在远场,旋流也在不断地拓展喷雾羽流的展项宽度．Masuda等[17]基于像素点强度的标准差与平均值的比值提出了羽流不混合度用来描述喷雾羽流空间分布情况,发现增加动量比或者降低We数可以得到更小的不混合度进而实现更好的混合．Patil等[18]研究了旋流对雾化羽流空间弥散特征的影响,通过Stokes数和粒径-速度图解释了旋流情况下液雾分散效果较好的原因,并拟合得到SMD与We数的关系式．

数值模拟可以为液体射流破碎机理以及雾化场浓度分布研究提供更精细化的结果,但目前采用数值手段研究旋流来流与射流的相互作用还比较少见．Prakash等[19]研究了旋流对射流轨迹、破碎长度和液滴速度分布的影响,发现液滴尺寸随旋流数增大而增大,并在下游发现了液滴的聚合现象．Jin等[20]采用数值方法研究了旋流对液体射流破碎机理的影响,发现旋流增强了方位剪切不稳定性波,导致液柱的背风面形成了两个液膜结构．然而,现有大部分相关研究均采用轴向叶片来产生旋流,旋流数小于1．近来,Xiao等[21]发现了一种蓝色强旋流火焰,其在燃烧过程中几乎没有烟尘产生．这种类似的强旋流构造或许可以为先进航发燃烧室设计提供一个新的思路．本文从强旋流角度出发,研究了宽范围旋流数(0～2.5)下液体射流的破碎雾化特征．本文第1节描述了主要的物理模型和数值方法;第2节研究了旋流数对液体射流喷注轨迹、破碎特征、液雾空间分布以及液滴尺寸的影响,并讨论了不同流向位置的液滴尺寸分布;第3节给出了文章主要的结论．

1 数值模拟方法及验证

1.1 控制方程和数值方法

本文采用Euler-Lagrange方法模拟了近场及远场的射流破碎雾化特征．在Euler体系中通过VOF方法追踪气液界面进而得到射流的破碎特征,液柱破碎后形成液滴;当VOF液滴满足一定条件时转化为Lagrange粒子,基于单个液滴的动力学模型模化液滴特性进而得到远场的粒径、速度以及浓度分布等特征．

1.1.1 VOF方法

Euler框架的控制方程为两相不可压缩的Navier-Stokes方程,可写成

∇·u=0,

(1)

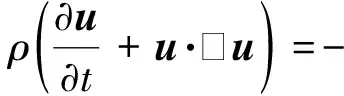
(2)

其中ρ为密度;u为速度矢量;p为压力;μ为黏性系数;D为应变张量,有Dij=(∂iuj+∂jui)/2;Fσ为表面张力,采用连续表面张力模型对表面张力进行模化:

Fσ=σκδsn,

(3)

其中σ为表面张力系数,κ为局部曲率,δs为Dirac函数,n为气液界面单位法向量;Fp为Lagrange粒子作用于连续相流体的力．

在气液界面冻结的情况下,基于上述公式可求解得到速度、压力．对两相问题进行求解时,还需要得到不同时刻的气液界面．在VOF方法中,通过相分数α对气液界面进行描述,α=0表示网格中全是气体,α=1代表液体,α在0和1之间则表示气液界面．通过标量输运方程对相分数进行求解进而得到每一时刻的气液界面:

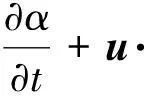
(4)

通过加权平均得到网格内部的密度和黏性系数:

ρ=αρl+(1-α)ρg,

(5)

μ=αμl+(1-α)μg,

(6)

其中下标l和g分别代表液体和气体．

1.1.2 LPT方法

VOF模型主要用于模拟射流从喷嘴内喷出破碎成液带和大液滴的过程．当大液滴进一步破碎成小液滴时,若液滴满足转化准则,则会将Euler体系的液滴转化为Lagrange粒子,通过离散相的形式对液滴信息进行存储．离散相粒子的主控方程为位移和动量方程:

(7)

(8)

其中mp,xp和up分别为粒子的质量、位置和速度;FD和FG代表粒子受到的气动阻力和重力．气动阻力基于固体球在气流中的阻力公式得到:

(9)

其中dp为粒子粒径,ug为气体速度,CD为阻力系数,基于Schiller-Naumann阻力模型对其进行估计[22]．此外,在LPT方法中,分别采用了Reitz-Diwakar二次破碎模型以及Nordin聚合算法模拟了液滴的破碎和聚合过程．

1.1.3 Euler-Lagrange耦合方法

在横向射流中,从液柱剥离出的液滴难以与液柱发生再融合,本文算例中能够发生融合现象的液滴数不足2%,单向转化与双向耦合计算的结果差别不大[22],故本耦合方法中仅考虑Euler相液滴向Lagrange粒子进行转化,未考虑Lagrange粒子向Euler体系的转化．算法主要分为3个步骤:1) 标记流场中所有连通的液块,即相分数大于0的区域; 2) 计算连通块的物理性质,如质量、质心、直径以及球形度等; 3) 基于转化判据对连通块进行判定,若满足判据,则将Euler体系的液体块转化为Lagrange粒子并移除Euler体系下的液体相分数信息．

本方法主要采用几何结构[22]作为VOF液滴向Lagrange液滴转化的标准,其主要包括液滴的最大尺寸和球形度．参考本文计算过程中最小网格尺寸为25 μm,选取了8倍网格尺寸即200 μm作为液滴转化尺寸判据．保险认为:当液滴直径中至少有8个网格时使用VOF方法足以解析其动力学过程,而此时使用Lagrange方法来描述液滴误差较大．且这一尺寸可以满足大部分液滴的转化,能够凸显VOF-LPT方法的加速优势．液滴能发生转化的最大球形度(最大直径与平均直径的比值)为2,与文献[22]一致．VOF-LPT耦合方法基于CFD开源工具包OpenFOAM v1912进行实现．其中通过interIsoFoam求解器使VOF方法得到的气液界面更加尖锐,进而得到更为准确的表面张力．

1.2 物理模型与数值设置

表1 射流液体以及来流气体物理性质

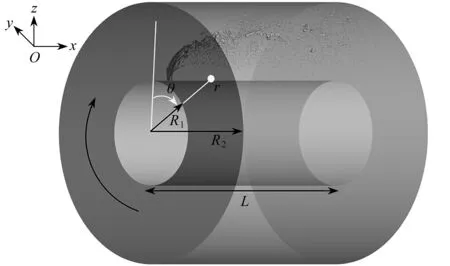
图1 旋流射流相互作用计算模型Fig. 1 Illustration of the computation setup for the swirl-jet interaction

旋流数定义为切向方向与轴向方向的质量通量之比[23],即

Ns=Gθ/(R0Gx),

(10)

其中

R0=R2-R1,

(11)

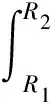
(12)

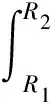
(13)

基于来流气体速度和旋流数可求解得到来流轴向速度和切向速度:

(14)

为研究射流在不同旋流强度下的破碎雾化特征,保证来流与射流的Re数不变,共设计了4个不同旋流数工况．旋流数Ns分别为0,0.5,1和2.5,4个工况下气体We数均为77,动量比q为10,射流出口平均速度Ul为8.29 m/s．入口切向速度u和轴向速度v通过旋流数和气体速度计算得到,如表2所示．

表2 不同旋流数下空气来流与射流的工况设置

液体射流假设为发展完全的湍流管道流动,射流出口平均速度分布采用工程中常用的1/7幂次率速度型[24],即

(15)

计算中湍流采用LES方法进行模化,亚格子模型采用动态的Smagorinsky模型．此外,采用自适应网格(AMR)技术在气液界面处进行了自适应加密．最高加密层数为3,计算域初始网格为400万,到计算终止时刻网格量达到了800万,加密后的最小网格尺寸为25 μm,沿喷嘴直径分布有16个网格,这足以捕获到主要的表面波、柱状破碎结构以及大液带的夹断动力学特征[25]．此外,关于横向射流的网格无关性验证可参考之前的研究[26]．

1.3 喷注轨迹验证

本文基于旋流数为0的射流喷注轨迹(横向射流结果)与实验结果进行了比较,对数值模拟方法进行验证．实验采用Gopala等[27]的喷注轨迹纠正公式:

在总额预付制下医保控费管理的检查主要分为三步实施。第一步，对医保总额的完成状况进行检查；第二步，按照DRG病种进行分析，找到对医保费用变化影响最大的重点病种，例如超过分摊权重20%的病种；第三步，由于医疗费用是由患者人数和患者均次费用两个指标共同决定的，因此可将医疗费用的变化分解为 “由于收治患者人数变化造成的费用变化”和“由于患者均次费用变化造成的费用变化”两类（见表2）。通过对重点病种医保费用的分解，找出引起医保总额超标的主要原因。

(16)

其中R为迎风面轨迹的径向高度,喷注轨迹主要与动量比相关．数值结果得到的迎风面喷注轨迹与实验结果的比较如图2所示,黑色方点为数值方法得到的喷注轨迹．在相同的动量比下,数值结果与实验吻合得很好．

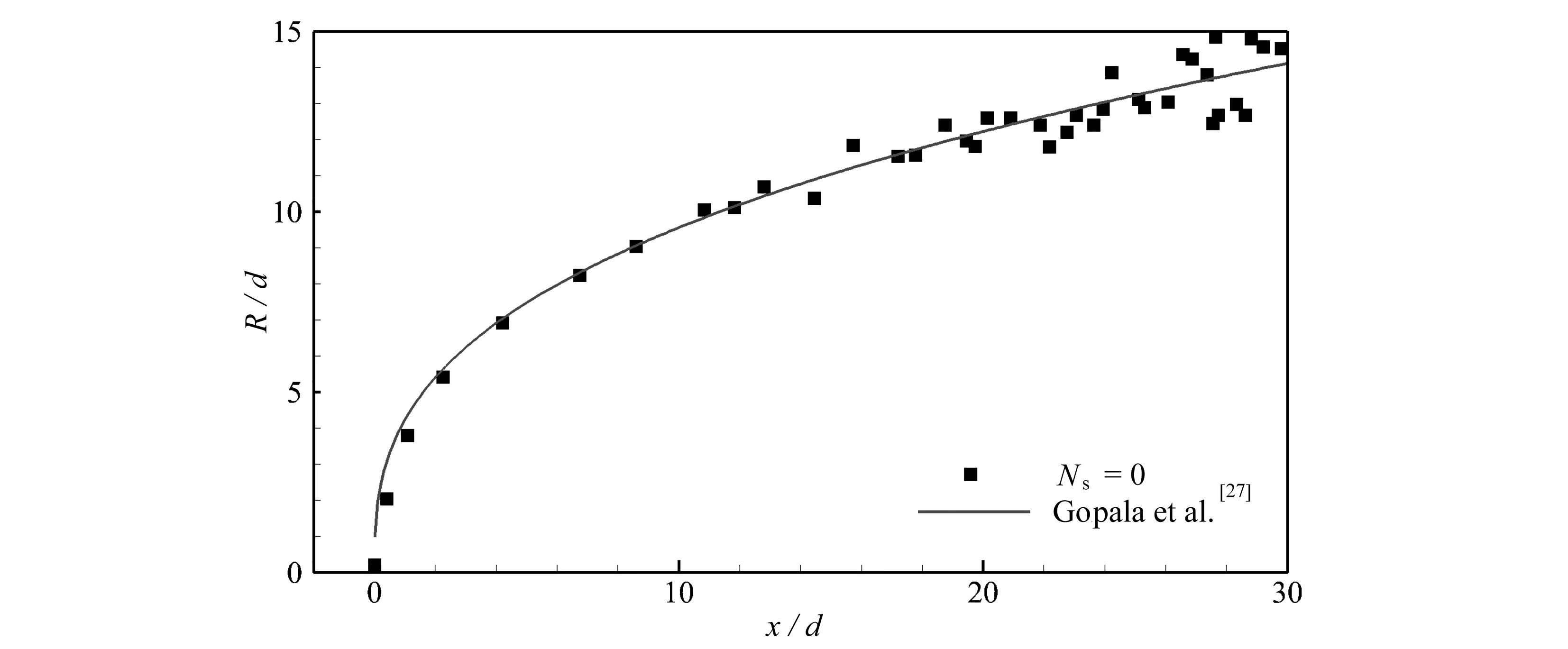
图2 旋流数为0的迎风面喷注轨迹结果与实验结果比较Fig. 2 Comparison of the windward trajectory with the experimental results for Ns=0

此外,基于旋流数为0的工况将射流破碎后液滴的SMD与实验结果进行了比较．实验采用Sallam等[10]基于边界层剥离理论提出的液滴粒径半经验公式:

(17)

其中νl为液体运动黏性系数,dp为从液柱表面剥离后的液滴直径．图3给出了旋流数为0时液滴粒径随径向高度的变化趋势并与实验结果进行了比较．其中红色圆点为破碎后液滴SMD分布,蓝色圆点为不同径向高度下液滴的平均直径,黑色虚线为实验结果．从图中可看出数值结果与实验结果吻合较好．数值结果表明随着径向高度增加,液滴直径逐渐增大,这是由于横向射流的不同破碎模态导致的．在近场液柱发生表面破碎,小液滴从液柱表面剥离;在射流远场液柱整体发生破碎,破碎后液滴直径与迎风面轴向不稳定性波的波长相关,液滴尺寸更大．

2 结果讨论分析

2.1 旋流对液体射流宏观形态的影响

图4展示了不同旋流数下射流在yOz平面视角的结果,采用y方向速度进行染色,从图4(a)—(d),旋流数逐渐增大．图4(a)是旋流数为0的射流结果,液柱基本沿yOz平面呈现轴对称特征．通过对比可知,随着旋流数的增加,射流逐步向右侧偏转,且随着旋流数的不断提高射流偏转程度逐步趋缓．图中红色和黑色箭头分别标出了不同旋流数下射流的破碎开始位置和液柱破碎位置．其中破碎开始位置定义为首次从液柱边缘剥离出小液滴的位置,而液柱破碎位置则是整个液柱完全破碎的位置．对射流的破碎开始位置和破碎位置的径向高度进行了提取,结果如图5所示．

图4 旋流与射流相互作用喷雾结构Fig. 4 The spray structure of the interaction between swirls and jets

图5 不同旋流数条件下破碎开始位置以及破碎位置的径向高度Fig. 5 Radial heights of the breakup onset and the breakup location for different swirl numbers

从图5中可看出,随着旋流数的增加,破碎开始位置的径向高度不断升高,说明旋流条件推迟了射流的表面破碎．这可能是因为复杂的旋转气流条件,使射流的方位剪切不稳定性波这类短波无法持续稳定地发展,进而推迟了表面破碎中液膜的剥离．而对于轴向表面波这类长波,强旋流条件能够增大扰动的波动幅度,使得液柱快速发生破碎,这在case 3中格外明显．故在弱旋和无旋条件下,破碎位置基本不变,而在强旋来流条件下,破碎位置的径向高度出现明显下降．此外,从图中还能观察到,随着旋流数的增大,雾化液滴向远离中心轴的方向发展,靠近喷嘴内壁面的液滴较少．这由破碎开始位置的上移导致,也进一步说明射流的初次破碎特征对后期的液雾场浓度分布影响重大．

图6展示了case 1(Ns=0.5)射流与旋流相互作用不同视角的雾化场．其中图6(a)—(c)采用y方向速度进行染色,图6(d)使用x方向速度进行染色．液体射流在旋流气动力作用下射流液柱向流向方向以及切向方向发生偏转,液柱在远场破碎雾化形成喷雾羽流．从图6(a)中可看出,在射流近场(x/d<8),不断有液带和小液滴从液柱表面剥离,这一阶段为表面破碎阶段．现存两种主流机理解释表面破碎:一种为边界层剥离理论[10],即由于来流气体与液柱横截面发生剪切作用,气液界面处液体边界层从迎风面向背风面不断发展,直至液滴的惯性力克服表面张力,最终从液柱横截面剥离出与边界层厚度相当的小液滴;另一种为方位剪切不稳定性理论[11],该理论从无黏角度出发,通过时空线性稳定性分析提出了横向射流液柱横截面存在类似于同轴射流的方位不稳定性波[28],并给出了方位剪切不稳定性波存在的判据以及增长速率,该类不稳定性波主要由剪切不稳定性主导,并伴有周向RT不稳定性的作用．图6(a)、(b)中圈出了在射流近场由于表面破碎形成的小射流分支/液膜,这说明射流的表面破碎为一个三维结构,由不同径向高度的不稳定波叠加形成,进一步验证了方位剪切不稳定性理论主控的表面破碎机理．其产生过程可解释为:在靠近喷嘴处(z/d<1),液柱横截面的不稳定性波不断增长;当不稳定性波扰动幅度达到与喷嘴直径相当时,从液柱两边剥离出液膜;进一步液膜在来流气动力作用下破碎形成孔洞,在液膜边缘液体聚集形成液带,进而在表面张力的作用下发生夹断形成液滴．图6(d)展示了液柱近场不同液体块表面轴向速度的分布情况,可以看到在液柱上随着喷注高度的增加,轴向速度不断增大;而液滴的轴向速度明显大于液柱表面速度,这是因为液柱破碎后形成的小尺寸液滴Stokes数较小,随流性变好．

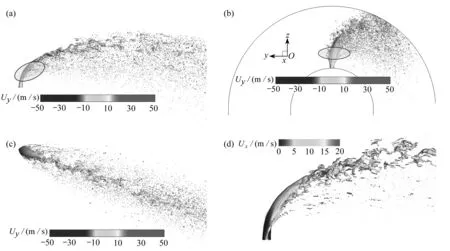
图6 旋流与射流相互作用喷雾结构三视图(a)—(c)及射流近场破碎结构(d)Fig. 6 Three views of spray structures (a)—(c) and the near-field break-up structure of swirling jet interaction (d)

2.2 射流近场破碎特征

图7展示了不同旋流数条件的射流的近场演化结果．结果显示,在case 0—case 2中,射流的背风面存在有两个射流分支,这与Jin等[20]观察到的现象一致．随着时间的演化,射流分支位置变化不大．当旋流强度逐渐增大到大于1时,出现了与文献[20]不一样的现象,两个射流分支随旋流强度增加逐渐靠拢,最终在case 3中融合为一个分叉．在强旋流作用下,射流除了表面破碎呈现出不同的射流分支现象外,在柱状破碎也呈现出较大的差异．在旋流强度较低时,射流表面破碎和柱状破碎区域分割较为明显,轴向不稳定性波结构离喷嘴较远,故在近场能够清晰地分辨表面破碎剥离的射流分支/液膜;随着旋流强度的增大,轴向表面波(KH不稳定性波)结构逐渐向喷嘴移动,波动幅度不断增大,最后在case 3中,轴向表面波融合了从液柱边缘剥离的液膜,使表面破碎区域融入柱状破碎过程．上述现象说明旋流,尤其强旋流,不仅能使液体射流发生偏转,也能够强化气液相互作用,使KH不稳定性波快速发展进而破碎射流,所以横向射流中的破碎机理无法直接应用于旋流与射流的相互作用过程．值得注意的是,在强旋流作用下KH不稳定性波的波长较大,这会导致较大的初始液块的产生．故而最后喷雾场的液滴粒径分布由两个竞争因素共同决定:一是旋流增强了气液相互作用,加速了液滴的破碎;二是强旋流条件增大了初次破碎后的粒径．

2.3 射流轨迹

在旋流来流作用下,射流喷注轨迹会沿着切向方向发生偏转,此时基于直角坐标的xOz平面投影得到的射流边界并非射流的真实喷注轨迹．需基于xOr平面投影得到沿径向方向的喷注轨迹．附录详细比较了基于不同投影方式得到的射流喷注轨迹,进一步说明了基于xOr平面投影得到沿径向方向的喷注轨迹的合理性．基于以上喷注轨迹提取步骤得到的轨迹与平均场结果如图8所示．

图8 柱坐标系下case 1的喷注轨迹与喷雾平均场结果Fig. 8 The injection trajectory and the spray mean field results of case 1 in the cylindrical coordinates

基于上述轨迹提取方式得到不同旋流强度下的喷注轨迹结果见图9．从图中可看出,沿径向方向的喷注轨迹随旋流数增大不断升高．当Ns较小时,喷注轨迹变化不大,当Ns大于1时,喷注轨迹变化非常明显．因为来流气体速度相同,轴向方向速度分量随Ns增大而减小,故射流沿径向方向能喷注更高．值得注意的是,case 3的喷注轨迹在射流近场超出了来流前缘位置,从而使得喷注轨迹格外的“笔直”．这是因为此时的旋流数大于1,切向方向的气体动量大于流向方向的气体动量．强烈的侧向风吹向液柱,使得液柱在近场沿着流向方向被拉伸变形,从而出现向前倾的现象．

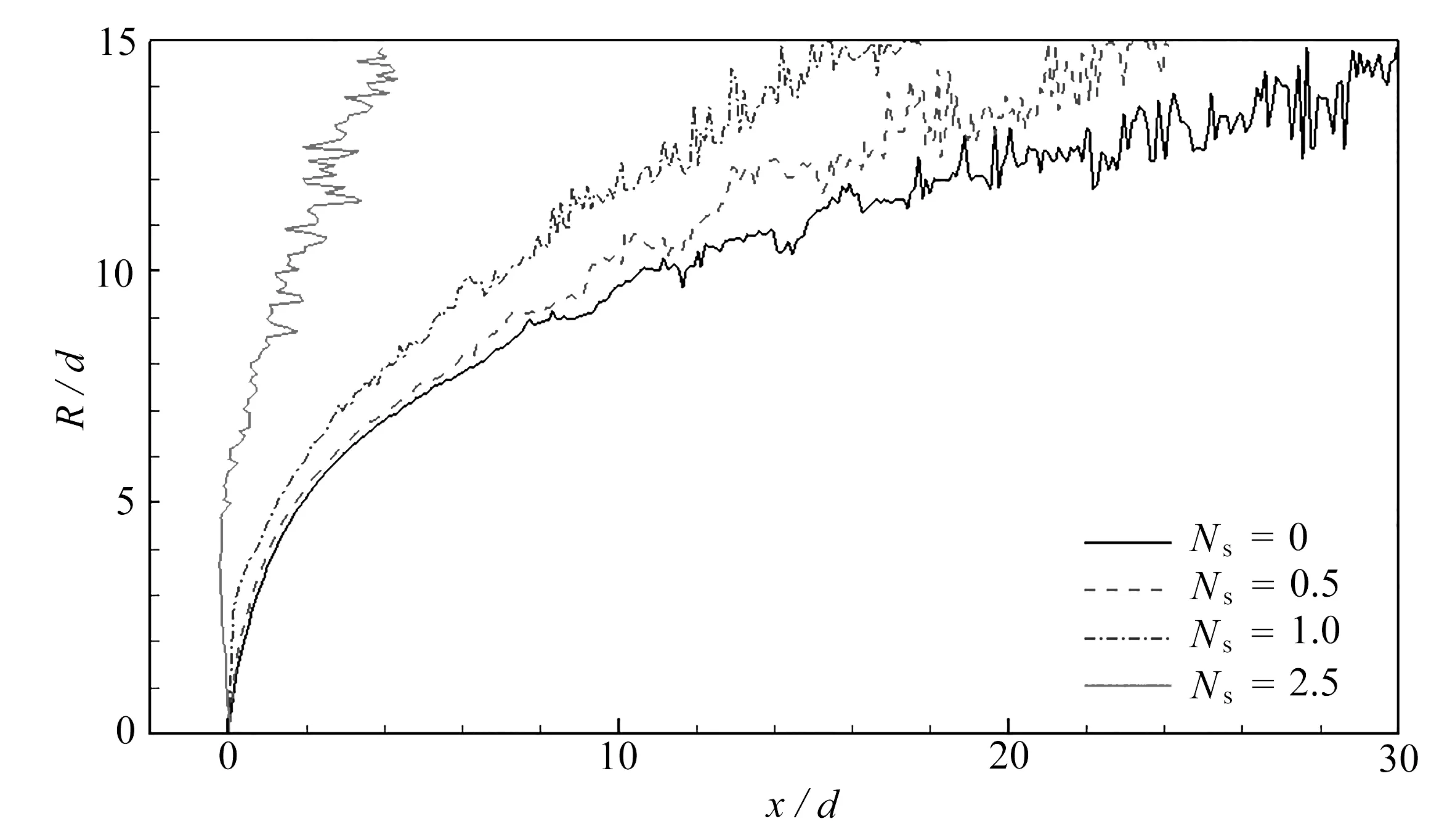
图9 不同旋流数下喷注轨迹比较Fig. 9 Comparison of injection trajectories under different swirling numbers

射流轨迹偏转角度提取与喷注轨迹提取方式类似,基于柱坐标系得到xOθ平面的流场．进行时间平均后选取喷雾羽流最浓厚的位置作为偏转角度数据点．射流轨迹偏转角度随轴向位置变化趋势见图10．从图中可看出射流偏转角度与轴向位置基本呈线性关系,且偏转角度斜率随着旋流数增大而不断增加．对case 1—case 3的偏转角度斜率进行线性拟合,得到斜率分别为0.896,1.916和3.514．

图10 不同旋流数下偏转角度结果Fig. 10 Deflection angle results under different swirling numbers

2.4 雾化液滴特征分析

2.4.1 液滴空间分布

图11展示了case 0—case 3在x/d=10位置处的液滴空间分布情况．从图11(a)中可看出,当没有旋流时,喷雾液滴主要集中在内壁面上方．当来流具有旋流特征时,液体明显偏向一边．从图11(a)—(d)可以看出,随着旋流数的增加,液滴分布逐渐向右侧偏移,且分布范围逐步增大,液滴密度也在增加．

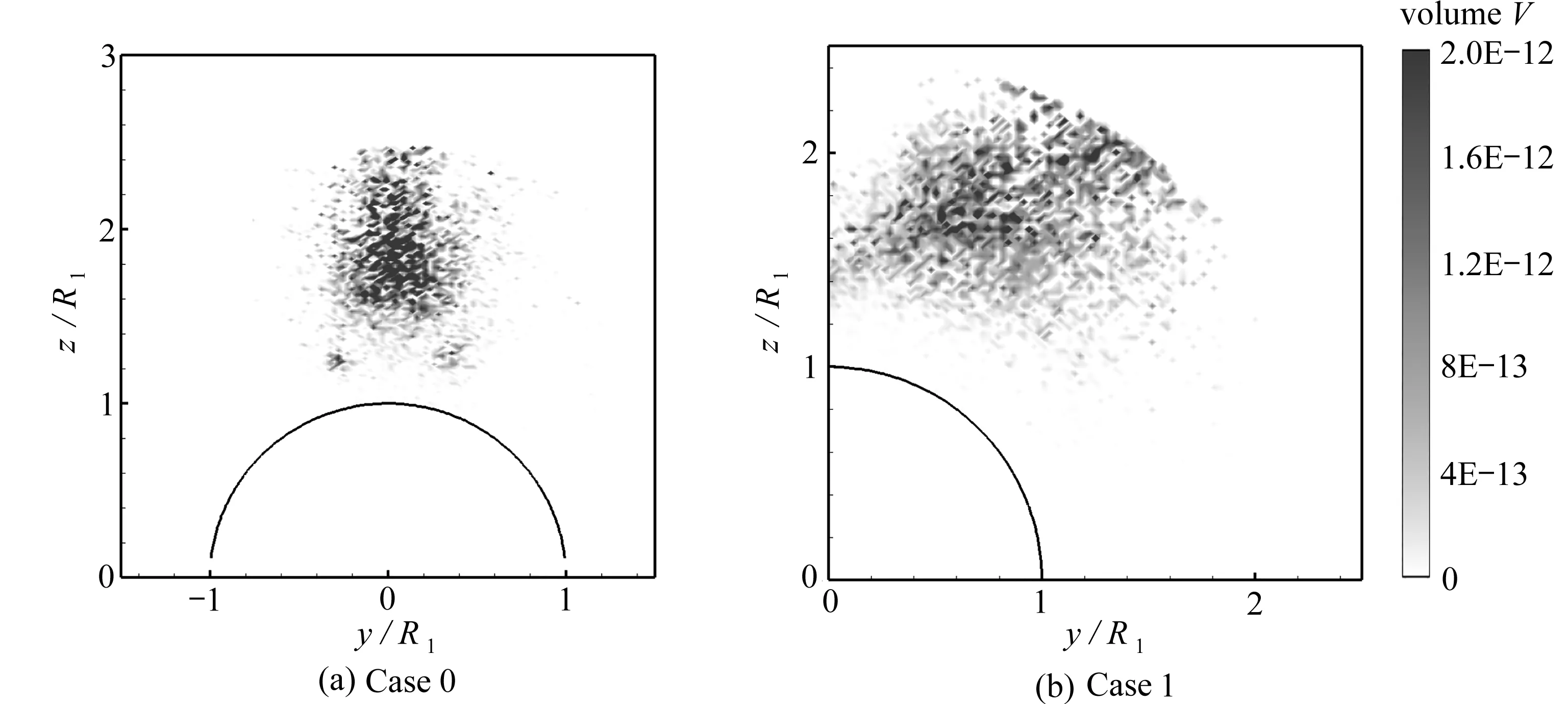
图11 Case 0—case 3在x/d=10处平面液滴空间分布Fig. 11 Spatial distributions of planar droplets at x/d=10 in case 0—case 3

图12为case 1(Ns=0.5)在不同轴向距离上的液滴空间分布,随着流向位置的增加,液滴空间分布整体变化不大,但是液滴重心略微向径向方向偏离．

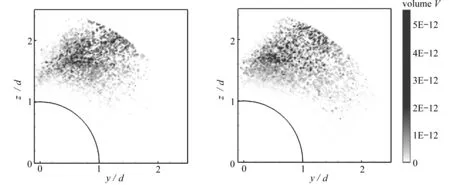
(a) x=10d (b) x=20d

2.4.2 液滴粒径尺寸和概率密度函数(PDF)

不同旋流数下射流破碎后平均SMD如表3所示．从表中可看出,SMD随着旋流数的增大而不断减小,这说明旋流的作用促进射流的破碎雾化．但当旋流数逐步增加时,SMD减小趋势放缓,SMD保持一个较低的值．图13展示了不同旋流度算例不同流向平面的液滴PDF分布．从图中可看出,随着旋流度的增大,PDF曲线逐渐扁平,结合整体的SMD结果可以说明在强旋流作用下流场中出现了更多的小粒径液滴,而曲线更高则说明流场中仍存在大液滴并未发生破碎导致流场粒径分布不均匀．针对同一旋流度,随着流向距离的增加,PDF曲线均有向扁平且向右发展的趋势,小粒径液滴更多,说明液滴粒径随着流向方向不断变小．

表3 不同旋流度下射流SMD结果

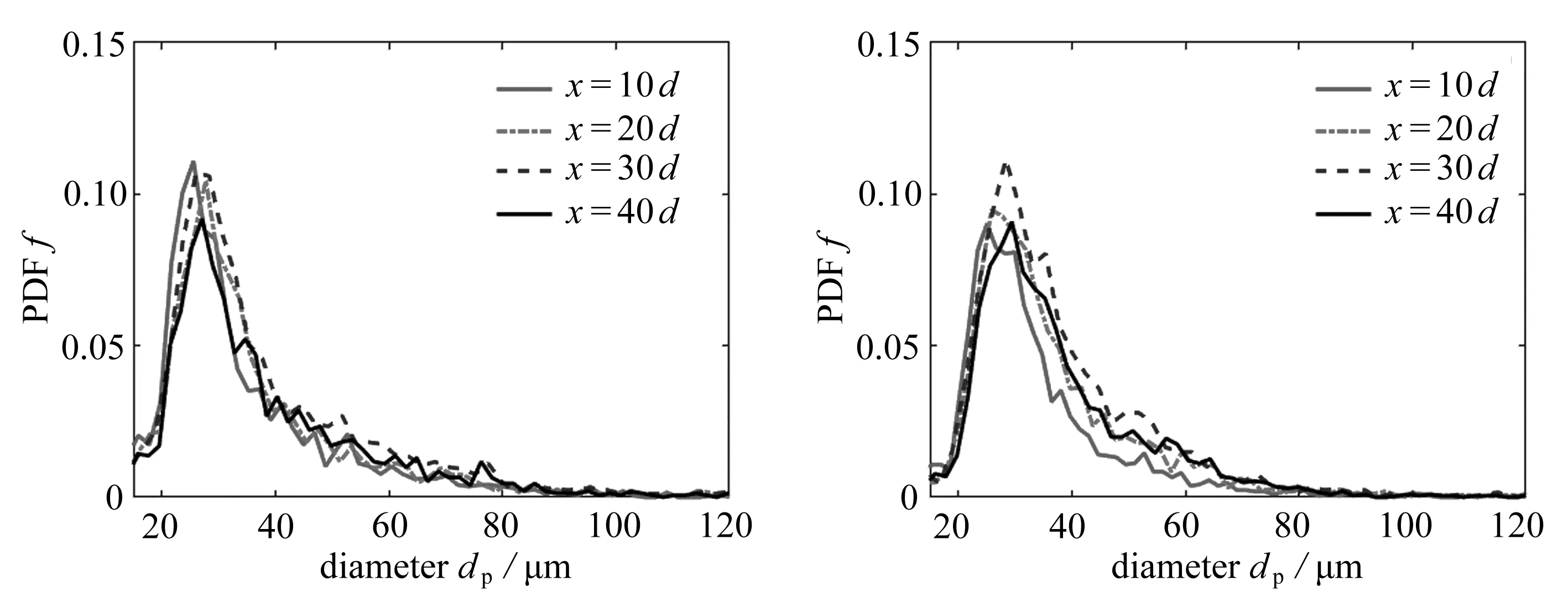
(a) Case 0 (b) Case 1

2.4.3 不同平面粒径分布

不同旋流数下x/d=10,20,30,40截平面的SMD大小如表4所示．可以观察到,随着旋流数的增加,在各个平面的SMD值逐步下降．在无旋流条件时,适当增加旋流度对SMD的作用显著．相较于其他位置,case 0和case 1在x/d=20和30之间的SMD值较大,这是因为这两个工况在x/d=10时处于表面破碎阶段,故粒径较小;而在x/d=40时,一次破碎后的大液滴在气流作用下进一步破碎,进而粒径减小．而在case 3中,强旋流作用下,射流在近场(x/d<10)发生了柱状破碎,得到较大的液滴从而SMD值最大;随流向距离增加,大液滴在强旋气动力作用下破碎成小液滴．这一现象也进一步说明了强旋加速了射流的柱状破碎．

表4 不同位置截面射流SMD结果

3 结论

本文研究了强旋来流作用下液体射流的破碎特征和雾化特性．液体射流的破碎包含柱状破碎和表面破碎阶段．强旋流条件能够增强射流的柱状破碎,推迟射流表面破碎的发生．KH不稳定诱导的轴向波的发展是射流发生柱状破碎的主要原因;强旋流条件增强了气液相互作用,使液体射流更快发生破碎．在表面破碎区域观察到射流分支/液膜从液柱表面剥离,这与射流横截面方位剪切不稳定波的发展密切相关．旋流作用下背风面的射流分支和轴向不稳定性波逐渐靠拢最终融合,抑制了射流的表面破碎,使得破碎开始位置的径向高度升高．射流沿径向方向的喷注轨迹随旋流数增大而升高;射流的偏转与流向位置呈线性关系,旋流数越大偏转斜率越大．

射流雾化场的平均SMD随旋流数增大而减小,液雾场的空间分布区域也随旋流数的增加而分布更广．在无旋流和弱旋流条件下,yOz平面上的SMD随轴向距离增加先增大后减小,这是因为在近场表面破碎形成了较小的液滴,在远场液滴发生破碎导致液滴粒径减小．在强旋条件下,yOz平面上的SMD随轴向距离增加不断减小, 射流的表面破碎和柱状破碎融合, 在近场发生一次破碎形成了较大的液滴, 随轴向距离的增加, 液滴不断破碎进而粒径变小．结果表明, 射流雾化场的液滴粒径以及浓度分布与射流近场破碎特征密切相关．

致谢本文的计算是在上海交通大学高性能计算中心支持的Π2.0集群上进行的,在此表示衷心感谢．

附录不同喷注轨迹提取方法比较

为说明旋流与射流相互作用研究中喷注轨迹提取方式选取的重要性,本文对基于不同平面投影得到的喷注轨迹进行了详细比较．基于xOz平面投影的轨迹提取步骤可分为3步:第一步是得到不同时刻xOz平面投影的喷雾平均结果;第二步对平均喷雾场结果进行二值化,其中二值化使用的阈值通过MATLAB的graythresh函数自适应得到;最后对喷雾边界点进行提取得到喷注轨迹．

图A1 Case 2的xOz平面(a)和xOr平面(b)喷雾平均结果比较Fig. A1 Average sprays of xOz plane(a) and xOr plane(b) in case 2

类似于xOz平面投影的轨迹提取方式,本文的喷注轨迹提取步骤可分为4步:第一步是将直角坐标系(Oxyz)转化为柱状坐标系(Oxrθ),得到射流在沿着xOr平面的轨迹图像;随后对于不同时刻的喷注轨迹图像生成图像并得到不同时刻的平均场结果;然后对平均场结果的图像进行二值化,其中二值化使用的阈值通过MATLAB的graythresh函数自适应得到;最后对喷雾边界点进行提取得到喷注轨迹．

图A1展示了case 2基于xOz平面投影和xOr平面投影的喷雾场平均结果．从图中可看到沿轴向方向的远场区域,基于xOz平面投影的喷雾出现明显的向下偏转的情况,而xOr平面投影的喷雾轨迹随轴向距离增大而升高,直至外壁面．通过对图A2中轨迹的比较更能明显地看到,当x/d>10时,两种轨迹提取方式得到的喷注轨迹会出现较大的偏差．故在旋流射流相互作用实验中,当旋流数较大时基于背景光实验测量的喷注轨迹数据仅能用于近场．

射流轨迹偏转角度提取同样分为4步:第一步是将直角坐标系(Oxyz)转化为柱状坐标系(Oxrθ),得到射流在沿着xOθ平面的液雾投影图像;第二步对不同时刻的喷注轨迹生成图像并得到不同时刻的平均场结果;然后对平均场结果的图像进行二值化,其中二值化使用的阈值通过MATLAB的graythresh函数自适应得到;最后针对每一个轴向坐标,获取喷雾场的浓度平均θ坐标,如图A3所示．