基于可变采样周期滤波算法的电网电压序分量快速提取方法
2023-10-19郝捷刘新元何彩红曲莹李明贤
郝捷,刘新元,何彩红,曲莹,李明贤
(1.国网山西电力科学研究院,太原 030000; 2.国网朔州供电公司,山西 朔州 036000;3.中国矿业大学 电气与动力工程学院,江苏 徐州 221116)
0 引 言
电网电压出现不平衡故障时会对并网逆变器系统的稳定运行造成很大的影响[1]。快速准确地获得不平衡电网电压的基波序分量,是保证并网逆变器正常运行、实现相位检测、频率检测等的重要条件[2-3]。
当电网电压不平衡时,dq坐标系中会出现直流分量和二倍频交流分量。通常需要设计滤波器用于滤除二倍频交流分量,同时提取直流分量。而现有的谐波影响抑制方法多以使用低通滤波器为主,但是实际应用中很难做出理想的折中方案,来同时增大带宽以提高动态响应速度和降低带宽以使充分衰减谐波[4]。文献[5]采用了延迟信号消除(Delay Signal Cancellation, DSC)法分离电压正负序分量,但会延时1/4个工频周期。文献[6]对DSC法和滑动平均滤波(Moving Average Filter, MAF)法进行了详细的比较,表明这两种方法一定条件下是等价的,MAF算法同样存在响应速度缓慢的问题。文献[7]中提出仅在循环中级联一个DSC模块和一个MAF模块用于分别消除奇数和偶数谐波的方法,但是MAF模块会引入一个等于滑动长度的时间延迟,这会降低瞬态响应速度。文献[8]中,自适应陷波滤波器被并入锁相控制环路中,以选择性地消除所需频率的谐波分量,但是陷波滤波器不能处理负序分量。文献[9]中采用双二阶广义积分器来提取电网电压的正序分量。但是,这种双二阶广义积分滤波器难以有效滤除低阶频率分量。文献[10]提出了一种解耦双同步参考坐标系来检测正序和负序分量。该方法虽然能够有效提取正序和负序分量,但系统控制结构复杂,计算量较大。文献[11]中提出一种正序分量快速提取方法,可直接获得不平衡电网电压的序分量,但提取过程需要构建虚拟正交信号。文献[12]中提出一种改进型的DSC算法在两相静止坐标系下快速分离序分量,但是没有考虑随机噪声的影响。此外,一些电网频率估计技术值得引入正序分量提取的应用中[13],但是与电力系统频率估计的应用场景不同,对于基于嵌入式控制器的并网变流器系统,相应的算法应简单可靠且易于实现,并且可以在电力电子设备的开关周期(ms级)内完成[14]。
因此,为进一步提高正序分量提取的响应速度,文中提出了一种可变采样周期滤波算法(Variable Samplings Filter, VSF)。根据该算法的噪声放大规律,采用调节VSF算法的运算周期将电网电压中随机噪声的影响限制在可接受的范围内。通过MATLAB仿真和物理实验验证表明,文中所提VSF算法与经典的DSC算法相比在响应速度上具有的明显优势。
1 旋转坐标系下电压分量提取方法
由对称分量法可知,三相不对称电网电压可以表示为:
U=U++U-+U0
(1)
式中U+、U—、U0分别为的正、负、零序电压瞬时分量,可以分别表示为:
(2)
(3)
(4)
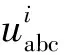
(5)
三相电压经过同步旋转坐标变换,可以描述为:
(6)
其中:
(7)
将式(5)代入式(6)进行旋转坐标变换,得到:
(8)
由式(8)可知,三相不平衡电压经过同步坐标变换之后在dq坐标轴的时域上含二倍频交流分量。
当前,最有效的二倍频交流分量滤除方法之一是DSC算法[5]。DSC的基本原理如下:
(9)
类似地,可以获得Uq的上述关系表达式:
(10)
但是DSC滤波方法来消除上述二倍频至少需要1/4个工频周期。这也就表明了在系统的起始时刻以及电网故障后的1/4个工频周期内,DSC滤波方法无法分离电压分量,延长了逆变器响应时间。
文中提出的基于VSF算法的电压分量提取方案为:通过对dq坐标系下的电压直流分量分量延时一个和两个采样周期来分别提取直流分量与二倍频交流分量。
因此,将式(8)中的t替换为代入t+Δt,t-Δt,化简可得:
Ud(t+Δt)=Udcos(2ωΔt)+Uqsin(2ωΔt)+
(11)
Ud(t-Δt)=Udcos(2ωΔt)-Uqsin(2ωΔt)+
(12)
Uq(t+Δt)=Uqcos(2ωΔt)-Udsin(2ωΔt)+
(13)
Uq(t-Δt)=Uqcos(2ωΔt)+Udsin(2ωΔt)+
(14)
联立式(11)、式(12),得到基波直流分量在dq坐标系下可以表示为:
(15)
同理,联立式(13)、式(14),二倍频交流分量在dq坐标系下可以表示为:
(16)
综上所示,其工作原理如图1所示。
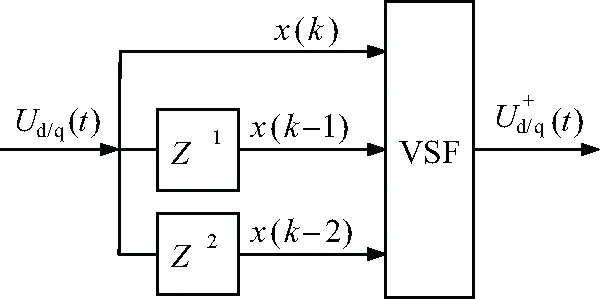
图1 VSF算法原理图
2 VSF算法的噪声放大分析及优化策略
根据VSF算法基本原理,以上述Ud(t)滤除二倍频交流分量为例(Uq(t)同理),其在第k次采样时的基波直流分量可以描述为:
(17)
考虑高频随机噪声时,将式(17)重新描述为:
(18)
且:
(19)
式中|xn|为可能的最大噪声值;Amax为最恶劣条件下的噪声放大系数,且:
(20)
显然:
(21)
文中提出的滤波方法的准确性不会因为采样频率的降低而降低,因而可以通过对VSF算法中运算周期进行缩放,将噪声水平限制在可接受的范围内。
Tc=CΔt
(22)
式中Tc为运算周期;C为采样时间间隔的缩放系数。
同时采用运算周期代替采样周期,响应时间与运算周期相同,此时噪声最大噪声放大倍数为:
(23)
如图2(a)所示,考虑最恶劣条件下的响应时间随着C的增加而线性地增大,而图2(b)则显示最大噪声放大倍数随着C的增加而显著地降低。

图2 噪声放大倍数及响应时间与缩放系数的关系
根据实际应用场景中随机噪声存在情况来折中考虑C的取值,可以有效地降低提取电压信号中的噪声影响,同时保证算法具有较快的响应时间。
此外,在快速消除dq坐标系中的二倍频交流分量后,采用串联的MAF模块对剩余的高频随机噪声进行完全滤波[6],为此,该方法结合了MAF算法和VSF算法的优点来分别消除电压中的高频随机信号和二倍频交流分量。
因此,图3所示的完整算法结构具有响应速度快和抗噪声能力强的特点。

图3 基于VSF算法的序分量提取方案
3 实验结果与分析
文中在MATLAB/Simulink中搭建的仿真模型,以提取dq坐标系下直流分量为实例对VSF算法的可行性进行验证。三相电压信号通过同步旋转坐标变换后,使用VSF算法快速提取直流分量。然后与相同实验条件下DSC算法进行对比。DSC算法滤波不会放大噪声信号,将其d/q轴输出的电压信号作为参考,评估VSF算法的噪声免疫能力。
仿真工况设置为:将三相电网电压中加入随机噪声信号,同时0.1 s时电压发生不平衡突变。其中,采样频率为100 kHz,VSF算法运算周期采用150倍采样周期,以确保噪声水平在可接受的范围内。同时串联截止频率为670 Hz的MAF模块,用来降低dq坐标系下高频噪声的影响。
图4(a)为三相电网电压于0.1 s不平衡突变的仿真波形原始信号。图4(b)为VSF与DSC算法滤除2倍频交流分量时,q轴电压的输出波形。VSF与DSC算法均能在电网电压不平衡且存在噪声的工况下提取直流分量。可以发现稳态情况下经过MAF算法增强后的VSF算法对噪声信号放大作用不明显。
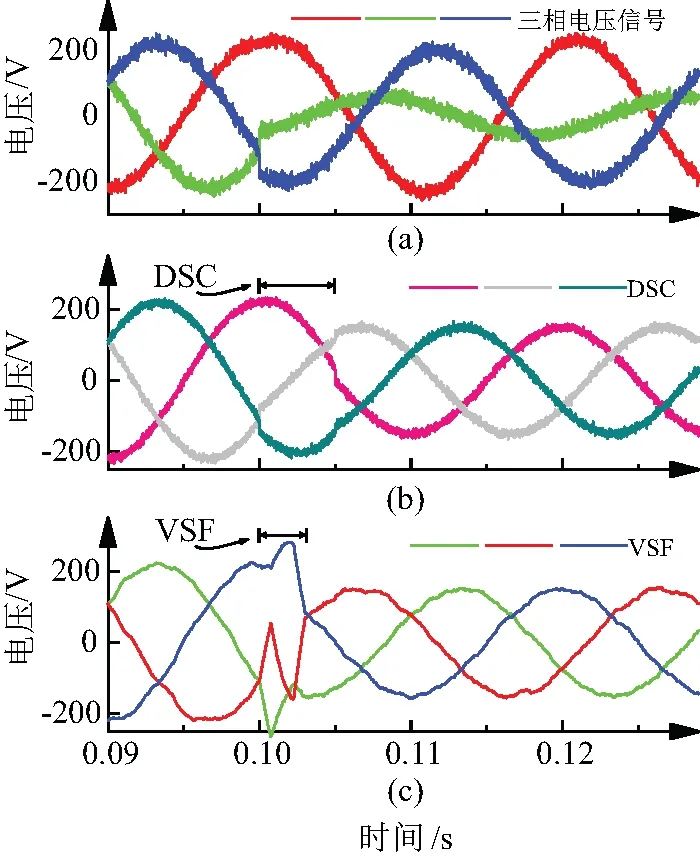
图4 仿真结果
特别是,经过VSF滤波算法的q轴电压中所含噪声较DSC算法更小。但是VSF与DSC算法动态响应时间却有较大差别,分别为3 ms,5 ms,与理论时间相同。因此,在低频分量时,VSF算法在动态响应速度上有明显优势。
图4(c)为VSF与DSC算法提取不平衡三相电压的正序分量的波形信号。结果表明,VSF与DSC算法可在三相电网电压不平衡且存在噪声的环境下,快速准确的获取正序电压分量。同时,从输出波形的暂态震荡幅度上来看,两种算法相差不大。但是从动态响应时间来上来看,VSF算法响应速度较DSC算法提高40%。综合动态响应速度、噪声免疫性以及稳态过程中的电压振荡幅度上来看,VSF算法的综合优势明显。
4 实验验证
文中通过以TMS320F28335 DSP为核心控制器,验证所提出的VSF算法的正确性和先进性。使用实时仿真平台对不平衡电网电压信号进行模拟,采样频率为20 kHz。算法输出结果通过数字控制系统额外提供的D/A转换器传输到示波器。在实验场景中,不平衡电网电压的工作状态突然发生,如图5(a)所示。此外,实验过程中的算法参数与仿真设置相同。

图5 实验波形
图5(b)、图5(c)分别为VSF与DSC算法滤除二倍频交流分量时,d轴与q轴电压的输出波形结果。性能比较结果表明,在电网电压不平衡的情况下,两种滤波算法都可以有效消除d轴和q轴上的二倍频交流分量。但是,VSF和DSC算法的动态响应时间相差很大:分别为3 ms和5 ms,与理论时间相同。其中,文中所提算法的响应时间比经典DSC算法短40%。
此外,VSF算法也没有噪声放大问题,这对于工程应用至关重要。用图3中的算法检测不平衡电网电压的正序分量,其二倍频交流分量滤波块全部由开发的VSF算法实现。如图5(d)所示,实验结果表明,在开发的VSF算法的帮助下,该应用程序执行良好,并实现了最快的响应速度。
综上所述,VSF算法快速准确,具有较好的抗噪能力。此外,该算法的响应时间比DSC算法的响应时间短40%,这对于并网逆变器的高性能控制至关重要。通过缩放运算周期,VSF算法可以在一定程度上减少随机噪声信号的影响。
5 结束语
并网逆变器实现不同控制的先决条件是快速准确地获取电压序分量。研究所提出的VSF算法可以快速准确地完全滤除dq坐标系中的二倍频交流分量。所提算法的响应时间比经典DSC算法的响应时间短40%。同时,该算法可以避免系统的噪声问题,这对于并网转换器的高性能控制具有重要意义。此外,所提算法还适用于序分量分离、相位检测、电能质量控制、电网故障穿越以及功率变换器控制等场合,具有一定的应用价值。
