采用分数阶域MFL-Net的机械智能故障诊断方法研究

时培明, 焦 阳, 陈 卓, 许学方, 李瑞雄, 谯自健

(1.燕山大学 电气工程学院,河北秦皇岛 066004; 2.太原重工股份有限公司,太原 030024;3.西安交通大学 能源与动力工程学院,西安 710048;4.宁波大学 机械工程与力学学院,浙江宁波 315211;5.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室,南昌 330013)

目前,随着机械设备不断趋于智能化、自动化,机械设备运行的可靠性也需不断提高[1]。由于机械设备运行时间长、工况复杂、工作环境恶劣,轴承和齿轮等关键传动部件极易出现故障[2]。监测机械设备运行并采取有效的故障诊断方法,并及时准确地诊断出机械设备的故障,能够保障机械设备安全运行,减少或避免重大灾难性事故。

近年来,深度学习因具备强大的特征学习能力,且满足机械故障诊断的自适应特征提取要求,因此在智能诊断方面得到发展[3]。其中,卷积神经网络(CNN)是一种有监督的深度学习算法,在机械故障诊断中得到了大量应用。利用CNN构建多个卷积核,并对输入信号进行多层卷积和池化,有助于提取出信号中的故障特征信息。Mo等[4]提出了基于变分核的一维卷积神经网络,以实现机械故障诊断。Dong等[5]针对振动信号中包含信息可能不被充分利用的问题,提出了一种多流卷积神经网络模型。Fu等[6]提出了多尺度第一层卷积核深度卷积神经网络,该方法能够自适应地提取故障特征并进行故障诊断。虽然卷积神经网络已经被应用于机械故障诊断,但在实际工程中,由于运行环境恶劣,机械设备多运行于非平稳工况,信号会呈现出时变、非平稳等复杂特性[7],此时卷积神经网络难以有效提取信号中的故障特征,致使诊断精度不高。

作为一种统一的时频变换方法,分数阶傅里叶变换(FRFT)能够获得信号从时域逐步变化到频域的所有特征,且具有聚集信号能量的特性,适合于处理非平稳信号[8]。Wu等[9]提出了基于FRFT特征提取的电机多级精细故障诊断方法,成功提取出信号在分数阶域中最大投影方向上的微小故障特征。Chen等[10]为了对机械设备进行状态识别和故障诊断,提出了一种基于FRFT特征向量重构的机械设备故障诊断方法。

基于以上分析,笔者针对机械设备振动信号早期故障特征微弱且具有非平稳性的特点,引入FRFT,构建了一种分数阶域多尺度特征学习模块的轻量级卷积神经网络(MFL-Net)的机械智能故障诊断方法。首先,将原始信号进行FRFT操作,从而获取信号在时域和频域之间的多角度FRFT特征;其次,将其输入到MFL-Net中进行训练,得到故障诊断模型,并完成对机械设备的故障分类识别;最后,通过离心泵和滚动轴承数据集将该方法与其他机器学习以及典型CNN故障诊断方法进行了对比。

1 FRTR

从积分变换角度,一维信号x(t)的p阶FRFT的定义为:

(1)

式中:Xp(u)为x(t)的p阶FRFT输出;Fp为FRFT算子;Kp(t,u)为核函数;t为时间域坐标;u为分数阶域坐标。

核函数Kp(t,u)的表达式为:

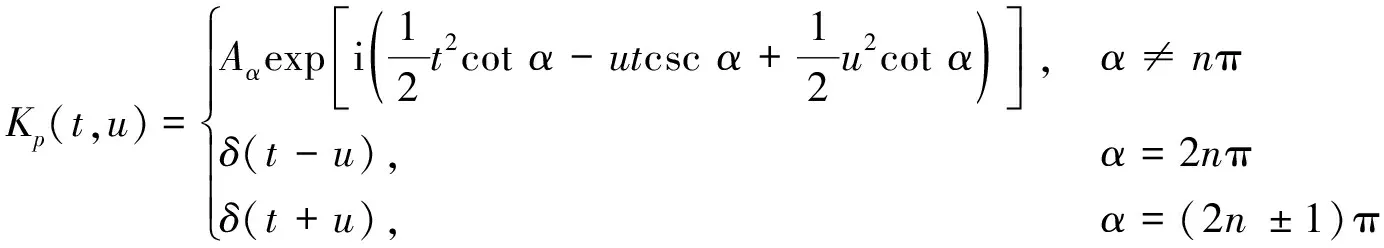
(2)

式中:Aα为FRFT的幅值;δ为狄拉克函数;α为时频平面的旋转角度。

p阶傅里叶变换坐标空间(u,v)是在原平面(t,w)上通过旋转对应角度α变换得到的,其坐标变换公式为:

(3)

式中:v为分数阶域坐标;w为频域坐标。

旋转角度α一般选取为逆时针方向的0～π/2。由于FRFT的周期对称性,旋转其他角度得到的结果均可以通过相应变换得到,所以无需选取其他角度来分析。

随着坐标轴的旋转,FRFT的分解基函数由单频正弦信号变换为线性调频信号[11],线性调频信号在分数阶域的变换如图1所示。

图1 线性调频信号在分数阶域的变换示意图

分数阶次p一般取0～1,阶次p从0到1的变化过程,也是原始信号逐渐变化到经典傅里叶变换的过程,即原始信号的FRFT。因此,通过FRFT改变p,便能获得信号从时域变化到频域的多角度特征。

2 MFL-Net

MFL-Net模型结构由4个多尺度特征学习(MFL)模块[12]组成,其中每个MFL模块后均添加有1个最大池化层,最后1个MFL模块的输出被传递到全局平均池化(GAP)层[13]和Softmax分类层,进而将每个输入特征进行分类。

2.1 微小模块

微小模块是一个3层模块,其输出表示为βmini,包括卷积(CONV)层、批归一化(BN)[14]层及线性修正单元(ReLU)[15]激活层。CONV层是使用3×3尺寸的卷积核从FRFT特征中提取更精准详细的故障特征,填充值保持“相同”,可以在整个MFL模块中保持相似大小的特征映射。BN层可以加快网络的学习速度,加速收敛过程,一定程度上防止过拟合的发生。ReLU激活层可以在网络学习的过程中引入非线性因素。微小模块的函数表示如下:

βN,mini(I)=λ(η(φ3,3,N(I)))

(4)

式中:I为输入;βN,mini(I)为具有N个卷积核的微小模块的输出;φf,f,N(I)为N个大小为f×f的核的卷积运算;η为BN函数;λ为ReLU激活函数。

2.2 MFL模块

MFL模块如图2所示,其由5个微小模块组成,用以多尺度特征的提取,使模型能够通过一组3×3小卷积核来学习感受野大小为5或7的特征,增强其学习过程,提高网络的泛化能力和图像识别性能[16]。相比于大尺寸卷积核,仅使用小尺寸卷积核即可大幅减少参数。2个1×1 CONV层可用于减少特征图中的通道数。

图2 MFL模块

MFL模块的函数β′表示为:

β′=βN,mini[βN,mini(I)]⊕βN,mini(I)

(5)

βN,MFL(I)=φ1,1,N[βN,mini(φ1,1,N(β′))⊕βN,mini(I)]

(6)

式中:βN,MFL(I)为输入I上具有N个卷积核的MFL模块的输出;⊕表示拼接操作。

2.3 整体网络结构

MFL-Net仅包含0.78×106个参数和1个MFL框架,且仅需较低的计算成本和存储空间,是一个高度轻量级的模型[12],其网络配置见表1。

表1 MFL-Net模型的结构参数

3 分数阶域故障智能诊断方法

采用分数阶域MFL-Net的机械智能故障诊断方法包括信号采集划分、FRFT、MFL-Net训练及故障诊断4个步骤,诊断流程如图3所示。

(1) 信号采集及标签数据制备:通过数据采集设备记录振动信号,得到不同健康状态下的原始振动数据,用one-hot编码读取类别标签并将每种故障数据划分为训练样本、验证样本及测试样本。

(2) FRFT:对上述得到的数据样本进行FRFT操作,通过将阶次从0开始按步长0.01递增至1,从而获得101个不同阶次下的数据,将其叠加在一起形成二维数据输出并转为灰度图,最终得到所需的FRFT特征。

(3) MFL-Net模型建立:按照上述设计的MFL-Net输入训练集FRFT特征进行训练,通过调整网络训练参数来获得训练效果最好的MFL-Net故障诊断模型。

(4) 模型诊断及验证:将测试集的FRFT特征输入训练所得模型中进行测试,得到不同故障的分类结果,进而验证分数阶域MFL-Net的机械智能故障诊断模型的准确性。

4 试验验证

4.1 试验一

4.1.1 试验说明

离心泵作为一种通用机械,被广泛应用于石油化工、航空航天、能源电力等领域,其健康状态对于整个装备安全运行至关重要。采用单体离心泵数据[17]对所提方法进行验证。试验在单体离心泵(ACM-0(AF))上进行。试验台的装置如图4所示。在离心泵上将4种不同的故障缺陷人工植入部件中,故障类型如图5所示。试验过程中参数设置见表2。

表2 试验一中的参数

(a) 离心泵试验装置

(a) 叶轮断裂

4.1.2 数据说明

离心泵数据共包含5种健康状态类型,分别为正常、叶轮断裂、叶轮堵塞、轴承内圈故障、轴承外圈故障。将离心泵各健康状态下的振动信号以2 048作为样本长度来截取样本信号,每类故障取1 000个数据样本,按照7∶2∶1的比例划分训练集、验证集和测试集,得到数据集描述,见表3。

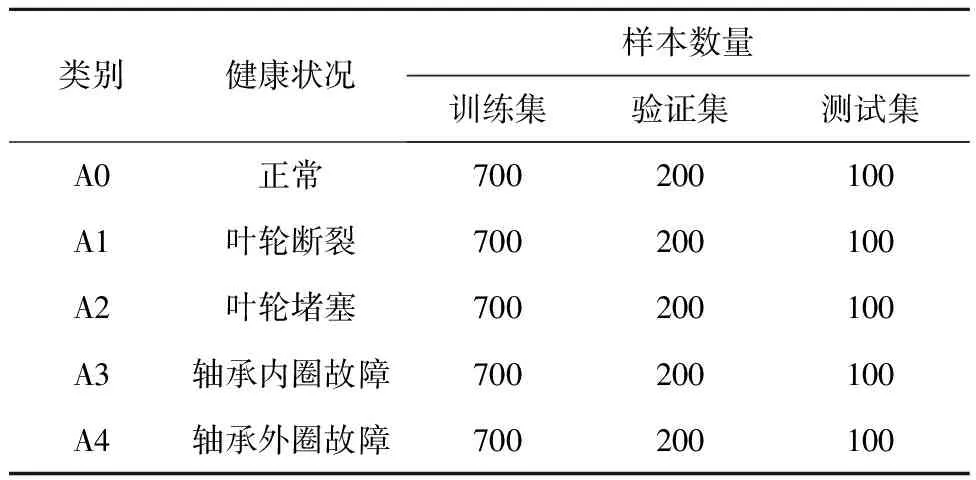
表3 试验一中的离心泵数据集

将得到的数据集输入分数阶域中,进行FRFT操作,改变阶次p来获得101个不同阶次下的分数阶域输出数据,叠加形成2 048×101的二维数据,将其转成灰度图后生成分数阶域样本特征。

4.1.3 试验结果

将样本特征输入至MFL-Net中,选择批处理数为16,迭代50次。训练集和验证集的准确率和损失函数如图6所示。由图6可以看出,模型训练效果良好,没有发生过拟合现象。

经过10次试验,诊断模型通过测试集的准确率均为100%。采用混淆矩阵对故障诊断模型的训练识别结果进一步分析,结果如图7所示。混淆矩阵显示5种健康状态类型的识别率均为100%,与总体准确率相对应。

图7 试验一中的混淆矩阵

4.1.4 t分布式随机邻居嵌入(t-SNE)可视化分析

为对网络学习的特征分布进行可视化分析,采用t-SNE处理由从MFL-Net的中间层中提取的特征,获得特征降维可视化图,见图8。从图8可以看出,原始数据经过FRFT操作后,各类特征表现出一定程度的聚集。在经过MFL-Net各层之后,各类特征已明显区分。

(a) 原始输入数据

4.1.5 方法对比分析

为了验证分数阶域MFL-Net的故障智能诊断性能,将其与MFL-Net和其他机器学习方法,包括自编码器(AE)、支持向量机(SVM)、长短期记忆(LSTM)网络进行了试验对比。AE采用3个中间隐含层的网络结构,各个隐含层分别有600、200和100个隐单元,选择Adam优化函数;SVM设置类型为1(V-SVC),核函数类型选择高斯核函数(RBF),RBF中的gamma值设置为100;LSTM堆叠层数设置为1层,输出维度为32,激活函数选择tanh。以上4种对比方法采用原始振动信号作为输入,各进行5次试验,各次准确率结果比较如图9所示。由图9可以看出,所提方法的准确率高于其他4种方法。

图9 试验一中不同方法准确率的比较

进一步将所提方法与宽卷积核深度卷积神经网络(WDCNN)、一维卷积神经网络(1-D CNN)和二维卷积神经网络(2-D CNN)进行比较。采用离散小波变换(DWT)对原始信号进行预处理,将其分解为LL、LH、HL、HH 4种高低频信号,再将4种信号组成四通道输入样本,将其输入到上述3种CNN中进行训练。WDCNN的输入为原始信号经DWT预处理后的一维数据,该网络由5个卷积池化层组成,其中第1个卷积层的核大小为64×1,其余卷积层的核大小均为3×1;1-D CNN的输入与WDCNN的输入相同,其网络结构包含2层交替连接的卷积池化层;2D-CNN的输入为原始信号经DWT预处理后排列为48×48的二维数据,其网络结构同样包含2层交替连接的卷积池化层。各方法分别进行5次试验,各次准确率结果比较如图10所示。

图10 试验一中典型CNN准确率的比较

从图10可以看出,所提出的分数阶域MFL-Net诊断方法相较于MFL-Net、AE、SVM、LSTM和其他一些典型CNN方法,准确率更高且结果更加稳定。同时,也表明对原始振动信号进行FRFT操作可以显著提高网络特征提取的性能。

4.2 试验二

4.2.1 试验说明

滚动轴承作为旋转机械三大关键部件之一,被广泛用于风电机组、机器人、轨道交通等装备中,能够及时诊断出轴承的微弱故障,为装备安全运行保驾护航。为此,将所提方法应用于滚动轴承故障[18]的诊断。试验轴承为圆柱滚子轴承,通过在轴承箱顶部安装加速计来测量试验台的振动信号。试验台装置如图11所示。

图11 试验二中的轴承试验装置

在轴承上将3种不同的故障缺陷人工植入部件中,故障类型如图12所示。试验过程中参数设置见表4。

表4 试验二中的参数

(a) 内圈故障

4.2.2 数据说明

滚动轴承数据共包含4种状态类型,分别为正常、内圈故障、外圈故障、滚子故障。将轴承各状态下的振动信号以2 048作为样本长度截取样本信号,每类故障取1 000个数据样本,按照7∶2∶1的比例将其划分为训练集、验证集和测试集,滚动轴承数据集描述见表5。

继续将得到的数据集进行FRFT操作,改变阶次p获得101个不同阶次下的分数阶域输出数据,叠加形成2 048×101的二维数据,将其转成灰度图后生成分数阶域样本特征。

4.2.3 试验结果

将样本特征输入至MFL-Net中,同样选择批处理数为16,迭代50次。训练集和验证集的准确率和损失函数如图13所示。

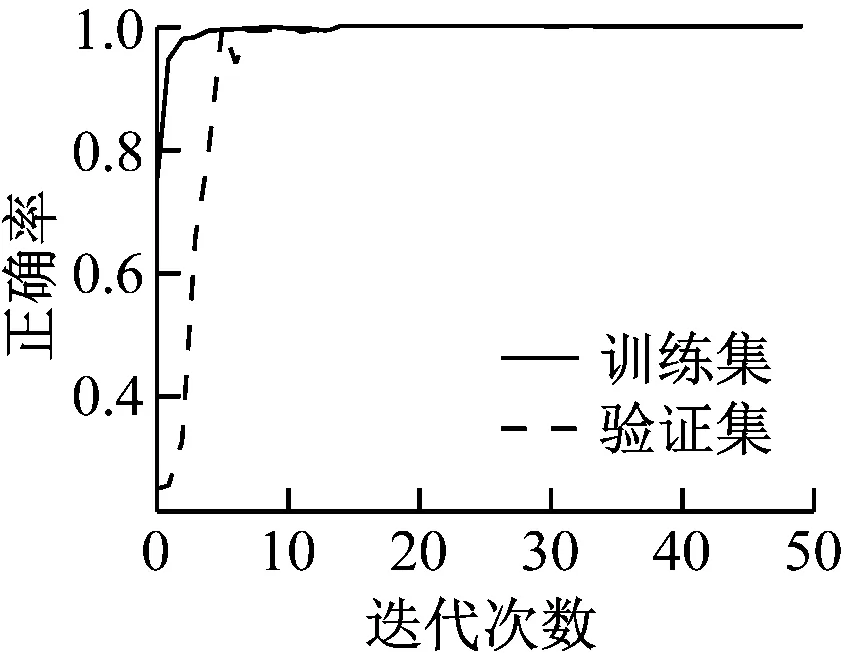
(a) 正确率

经过10次试验,该诊断模型在测试集的准确率均为100%,其混淆矩阵如图14所示。

图14 试验二中的混淆矩阵

4.2.4 t-SNE可视化及分析

采用t-SNE技术对MFL-Net的部分层提取特征进行降维可视化,如图15所示。由图15可以看出,原始数据在经过FRFT操作后,各类特征表现出一定程度的聚集,后经过MFL-Net各层之后分类特征更加清晰。

(a) 原始输入数据

4.2.5 方法对比及结果分析

将所提方法与MFL-Net、AE、SVM、LSTM进行对比,以上对比方法采用原始振动信号作为输入,各进行5次试验,各次准确率结果比较如图16所示。由图16可以看出,LSTM在此数据集上的诊断性能最差,且所提方法的准确率高于其他4种方法。进一步将该方法与WDCNN、1-D CNN和2-D CNN进行比较,仍采用DWT对信号进行预处理,各方法分别进行5次试验,各次准确率结果比较如图17所示。由图17可以看出,1-D CNN和2-D CNN的准确率较低,所提方法的准确率高于其他方法。

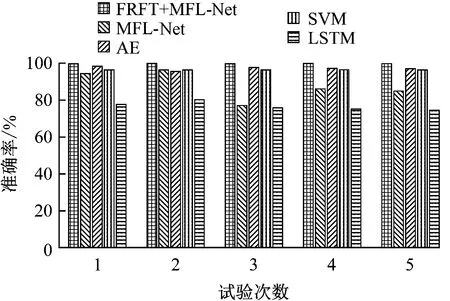
图16 不同方法准确率结果比较

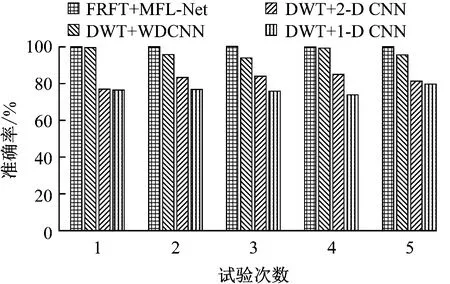
图17 试验二中典型CNN准确率的比较

综合2次试验对比结果可以看出,相较于MFL-Net、AE、SVM、LSTM和其他3种典型CNN,所提方法在2次试验中均达到了100%的准确率,表现出更加准确和稳定的性能。

5 结 论

(1) FRFT通过改变分数阶次可以获得原始振动信号在分数阶域的多角度信号特性,从而较好地展现非平稳信号的时频特征。

(2) 结合MFL-Net多尺度特征提取的优势,所提方法能够有效提取分数阶域时频特征中的故障信息,确保模型具有较高的诊断性能。

(3) 所提出的机械智能故障诊断方法可以达到较高的准确性,且相比AE、SVM、LSTM、CNN等传统故障诊断方法,所提方法的诊断准确率更高,结果更加稳定。