含LCL滤波的全桥变流器参数设计与改进控制策略
2023-10-19潘星辰兰德刚
兰 岚,潘星辰,兰德刚
(1.国网天津市电力公司高压分公司,天津 300232;2.国网天津电力党校(国网天津培训中心),天津 300171;3.国网天津市电力公司电缆分公司,天津 300160)
0 引 言
可再生资源的大规模开发利用是推动我国电力能源结构变革、支撑“双碳”重大战略目标实现的重要举措。电力电子变流器是可再生能源并网的核心装备,其运行控制效果直接影响电能变换效率、稳定性和谐波含量。目前,可再生能源并网广泛采用基于脉宽调制技术的电压源型变流器(voltage source converter,VSC),但由于VSC装置中的功率器件工作在高频开关状态,将导致大量与开关频率相同或是其整数倍的高次谐波混入电网,引发电磁兼容、污染电网等问题[1];因此,加入滤波环节去除电网侧高次谐波,已成为广泛采用的解决方案。
最传统的滤波方式采用单一电感滤波,其结构简单、易于实现,但所需开关频率高,电感量大,导致滤波器体积增加且造价昂贵。LC滤波器是另一种常用的滤波形式[2],在并网/独立双模式时效果明显,但在其他情况下则等同于单电感滤波,存在一定局限性。LCL滤波器是在传统滤波器基础上发展而来的新型滤波结构[3],在总电感量恒定的条件下,LCL滤波器比纯电感型滤波器抑制高次谐波的效果更加理想[4],比LC型滤波器更适合应用于开关频率低且功率大的场合。但LCL滤波结构为三阶,会出现谐振现象,威胁系统稳定,同时也增加了控制策略的复杂性,必须进行特殊参数设计。
为此,国内外开展了广泛研究:文献[5]提出一种LCL滤波器参数分步设计方法,降低了由频繁开关带来的损耗,同时保证了变流器的高性能;文献[6]提出一种用软件简化计算的通用参数设计方法;文献[7]提出一种基于筛选法和粒子群算法的LCL参数设计方法,提高参数设计环节的效率,但又会产生5倍谐波,系统中出现谐振的可能性变大。在控制策略中添加阻尼作用能有效解决此问题。有源阻尼法依靠对控制系统算法的修正来抑制谐振的影响,无源阻尼法则是在系统中加阻尼电阻来削弱谐振的峰值。如文献[8]提出一种“超前-滞后”的阻尼方法,减少了电流波形畸变率,也不增加额外的系统损耗,但其参数选择过程比较困难;文献[9]提出了虚拟电阻的概念,通过控制算法的特殊设计达到阻尼效果,不会增加额外的功率损耗,但增加了电流传感器的数量,放大了高频噪声,对变流器稳定性产生较大影响;文献[10]提出了一种反步法控制策略,省去了阻尼电阻。总体来看,电容串联电阻的无源阻尼法复杂度低,易于实施,具有较为广泛的应用场景。
针对整体变流器的控制策略,文献[11]提出了一种重复双闭环控制系统,基本消除了电网谐波带来的影响。文献[12]提出了嵌入式重复控制和N次陷波器相结合的方案,提高了稳态时的跟踪性能和动态特性。电压电流双闭环控制策略可以检测到电压和电流两个量的变化,并将其作为反馈量,达到动态响应与静态性能兼顾的效果,在全桥变流器控制中优势较大。
本文将LCL滤波器和全桥变流器相结合,对LCL滤波器的参数影响进行了分析,提出了电感、电容参数的设计方法,基于无源阻尼法实现了谐振抑制。提出电流内环准比例谐振(quasi-proportional resonance,QPR)控制、电压外环比例积分(proportional-integral,PI)控制的双闭环改进控制策略,通过数字仿真验证了本文设计方法和控制策略的有效性。
1 LCL滤波器参数设计
1.1 LCL滤波器数学建模
图1为单相LCL滤波器在频率较高时的等效电路。因L1和L2的附加电阻很小,研究中做忽略处理。按图中箭头所示方向选取电流的参考方向。

图1 LCL滤波器高频等值电路。
对于图1,依据基尔霍夫电压定律和电流定律,可以写出其数学模型。
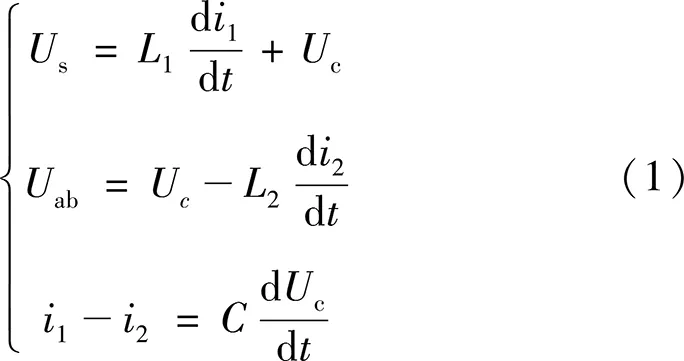
式中:L1为网侧电感,L2为变流器侧电感,C为滤波电容,Us为网侧电压,i1为网侧电流,i2为变流器侧电流,Uc为滤波电容两端电压,Uab为变流器交流侧电压。
将式(1)进行拉普拉斯变换,并将电网电压Us视为扰动,可绘制模型如图2所示。
据此可得到变流器交流侧电压Uab和电流i2之间的传递函数:
(2)
以及变流器交流侧电压Uab和网侧电流i1的传递函数式(即LCL滤波器在无阻尼条件下的传递函数):
(3)
式中:s可看作微分算子,将时域的参量进行微分即可对应复频域的参量,如时域的1,对应到复频域即为1/s。
由传递函数可以看出,LCL滤波器有两个零点和两个极点,较传统滤波器更为复杂。频率较低时LCL系统与L系统幅频特性大体相同,相频特性一致;频率较高时LCL系统衰减性能更好,但出现了谐振现象,对系统稳定性影响较大,必须采用适当的参数设计和控制方法消除LCL系统的谐振尖峰。
1.2 LCL滤波器参数设计方法
理论上,为抑制电网谐波,交流侧电感值越大越好,但系统的动态特性会随着电感增大而变差[13]。滤波电容增大,总谐波失真减小,但系统消耗无功增多,效率降低且动态响应变差,所以,滤波器参数的选取尤为关键。本文采用文献[14]中的方法,按补偿谐波电流的跟踪能力和变化率选择总电感值。其中,低频段和高频段分开考虑,再按最大谐波电流变化小于相电流峰值的5%计算得到总电感的范围,即
(4)
式中:Im为相电流峰值,fsp为采样频率,Udc为逆变器直流电压。
再由L2=3L1,求出各电感值大小,进而由式(5)计算电容大小:
(5)
式中:fres为谐振频率。
1.3 LCL滤波器的谐振抑制
如1.1节所述,LCL滤波器会出现谐振问题,所以需要额外调整控制方法或加入阻尼作用来抑制其产生的影响。LCL滤波电路的输入阻抗Zin和谐振频率ωres可分别写为
(6)
(7)
式中:j是复数,ω表示角频率,在频域分析中定义s=jω。
本文采用无源阻尼法,在滤波电容支路串联阻尼电阻,以抑制LCL滤波器的谐振现象。串联电阻R后,LCL系统传递函数变为
(8)
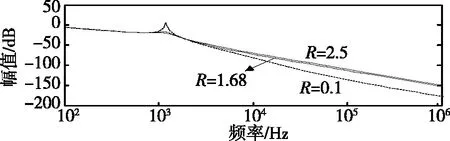
(a)不同阻尼电阻值对应的幅频特性曲线。

(b)不同阻尼电阻值对应的相频特性曲线图3 加入阻尼电阻后的LCL滤波器幅相特性。
可以看出,当电阻较小的时候,谐振频率处增益较高;随着阻尼电阻的增大,谐振幅值也得到了有效的抑制,且系统稳定性更好,但高频段滤波质量不理想、系统损耗增大。因此,阻尼电阻应满足有效抑制谐振幅值且取值尽可能小。由式(9)计算阻尼电阻的取值[15]。
(9)
2 含LCL的变换器改进控制策略设计
2.1 系统结构与数学模型
变流器电路拓扑结构如图4所示,其中Cd为直流侧稳压电容,用于减少直流侧电压纹波,起到缓冲作用,稳定整流后的电压;RL为负载电阻。
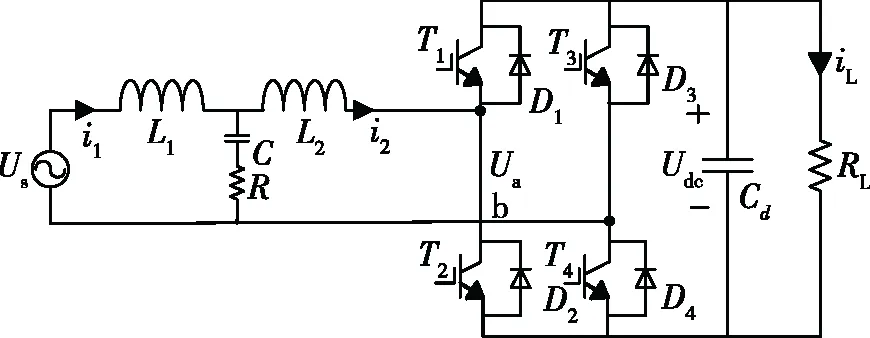
图4 含LCL滤波的全桥变流器。
本文采用图5所示的双闭环控制方式对变流器进行控制。将直流侧输出电压的控制放置于外环,采用比例积分控制器以保证响应速度。采用电流内环来控制交流侧电流,采用QPR控制以保证输出精度。为减少电网电压波动等对电流环的干扰,同时改善系统响应速度和抗扰动能力,还引入了电网电压前馈环节。

图5 双闭环控制。
2.2 电流内环控制结构
因为设计一般要求,电流要比电压变化速度更快,所以本文先对电流内环进行设计,如图6所示。
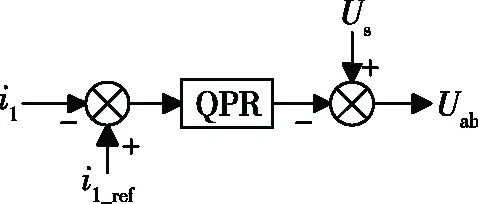
图6 电流内环控制。
根据框图可得内环控制策略数学表达式为

(10)
式中:i1_ref为网侧给定参考电流,GPR为PR控制器的传递函数。
电流内环采用PR控制器,可无静差跟踪电流,数字化处理过程也较为简单。但PR控制器在谐振点的幅值增益大,非谐振点幅值增益小,设计比较困难[16],因此可采用QPR控制,其传递函数为
(11)
将s=jω1带入GPR(s),即可得到基波频率下QPR控制的谐振增益:
(12)
式中:KPP为比例增益系数,KR为积分增益系数,ωc为截止频率,ω取100π。
可见,QPR控制可以很好地跟踪参考电流,但其增益由比例谐振的无穷变为有限值,可以根据实际需要来调节。
将QPR控制关系代入到式(10)当中,经过整理变换后可得到:
i1(s)=H1(s)·US+H2(s)·i1_ref
(13)
(14)
(15)
式中:L=L1+L2,A=CL1L2。
可以看出,通过调节H1(s)和H2(s)即可控制i1和i1_ref的关系,使之跟随参考电流,减小因电流波动带来的影响。当系统中电容、电感等参数设定好后,只需选择适当的准比例谐振控制器参数就可以实现这一目标。
2.3 电压外环控制结构
双闭环控制策略中,电压外环的输出作为电流内环的输入,二者相互影响,但由于内环速度比外环的速度快十倍以上,因此在进行外环的设计时可将电流内环部分等效看做一个简单的比例环节,其值为1,再忽略掉开关管上的电压即可得电压瞬时值uab=udc。
外环电压控制采用的PI控制器传递函数为
(16)
式中:KP为比例增益系数,Ki为积分增益系数。
Ki变大,积分速度减慢,超调量减小,利于系统稳定,但因其增益比较小,不利于消除静态误差,所以PI控制器参数的选取需综合考虑以上因素。电压外环控制如图7所示。
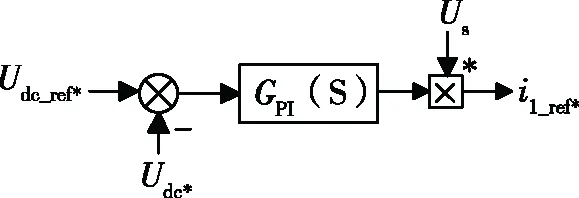
图7 电压外环控制。
PI控制器的引入为系统增加了一个开环极点,提升了系统型别,可以减小稳态误差;同时也增加了一个开环零点,提高了阻尼程度,可以缓解极点对系统产生的消极影响。适当调整PI控制器参数即可达到稳定直流侧电压的目的,使之等于给定的直流侧参考电压。电压偏差值和电网电压相乘后得到网侧输入电流参考值,即

(17)
式中:Udc_ref*表示直流参考电压标幺值。
因为单相脉宽调制(pulse width modulation,PWM)变流器的直流侧电压中固有二倍于基波频率的纹波,会对网测电流产生谐波的影响。假定只考虑基波频率整数倍的谐波电压,电网电压瞬时值us可以用式(18)进行描述:
(18)
式中:Usm为电网电压基波幅值,Usm i为第i次谐波电压幅值,k表示任意整数。
因为有谐波电压的存在,使变流器输入功率也含二次脉动分量及其他基波频率整数倍次功率分量,所以直流侧也会产生相应频率的脉动电压。因为控制策略选用双闭环,所以交流电流中含有三次谐波。经开关管后又产生四次纹波电压,最终整流所得直流电压里会有偶次纹波,交流电流里含有奇次谐波。
3 考虑谐波和电压波动的策略改进
3.1 谐波补偿方法
在第2节所述的比例谐振控制器的研究基础上进行了改进,并对三次谐波进行了补偿。具有补偿谐波环的准比例谐振传递函数为
(19)
式中:KrH、ωcH为H次谐波的准比例谐振控制器参数,KrH为积分增益系数,ωcH为截止频率。
在QPR控制器中加入以上三次谐波补偿环节后,其对应的幅频特性曲线如图8所示。可以看出,增加一个特定的谐波次补偿环后,谐波频率处增益变大,实现了对三次谐波的无静差跟踪,降低了谐波含量。
但由于原控制策略中参考电流是由电网电压和PI控制器输出信号相乘而得,故电压环输出的参考电流信号中同样包含谐波分量,可能限制谐波补偿环节的滤波效果。因此,本文在原控制策略基础上,进一步加入带通滤波环节,来滤除参考信号中的三次谐波,其传递函数为
(20)
式中:g为增益,n为滤波器带宽,ω1为基波角频率。
带通滤波器在除基波频率外的各处增益均为负值,可以实现滤除基波以外各频次谐波分量,但也会出现超调量,降低超调量必然会牺牲响应速度。
3.2 控制环节的限幅
在电网电压的突然跌落再回升的瞬间,或者瞬时过电压等情况下,会给系统带来相当大的冲击,若不对此加以控制,控制系统有可能失稳,甚至一次设备会因过流而受到损伤,进而造成安全隐患。因此,需要在控制环中加入限幅装置,将参考电流信号的幅值限制在安全范围内,确保网侧电流不会因过流影响运行安全。一般来说,变换装置出厂时已经考虑了一定的抗冲击能力,因此,考虑实际电流的波动范围,本文按照最高不超过额定电流的1.1倍设置限幅环节。
4 算例分析
采用图4所示的电路结构进行算例分析,电路参数如表1所示。其中滤波电感、电容、阻尼电阻数值由第1节所述方法计算得到。
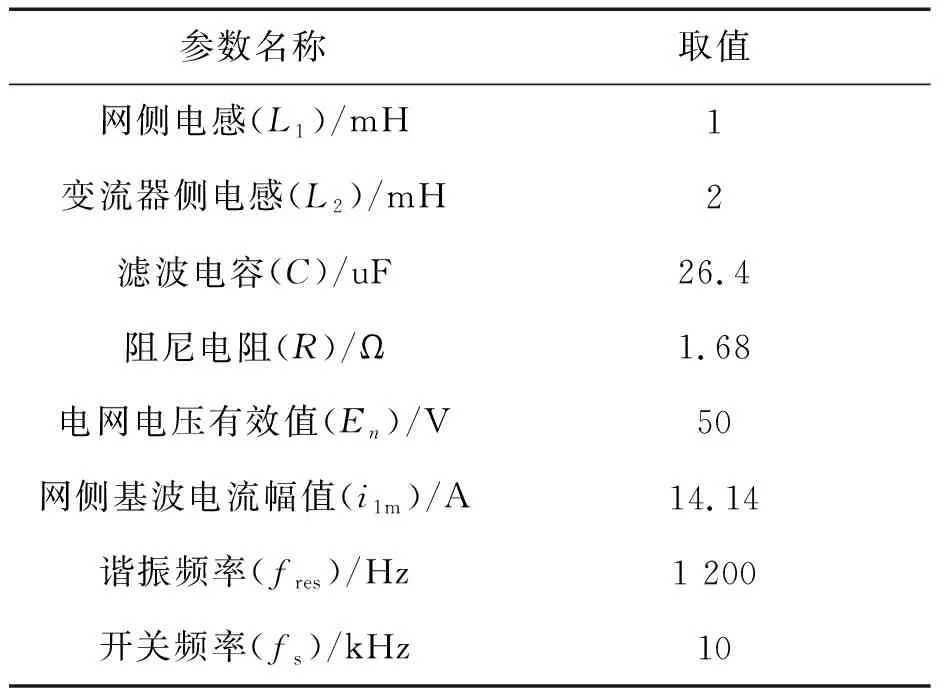
表1 LCL滤波器及变流器参数
4.1 谐波抑制效果分析
为验证控制策略的滤波效果,于0.083 s时在电网电压中加入幅值为10 V的三次谐波,如图9所示。未加入滤波控制时的稳态电网电压和电流,如图10所示。

图9 加入三次谐波后的电网电压。
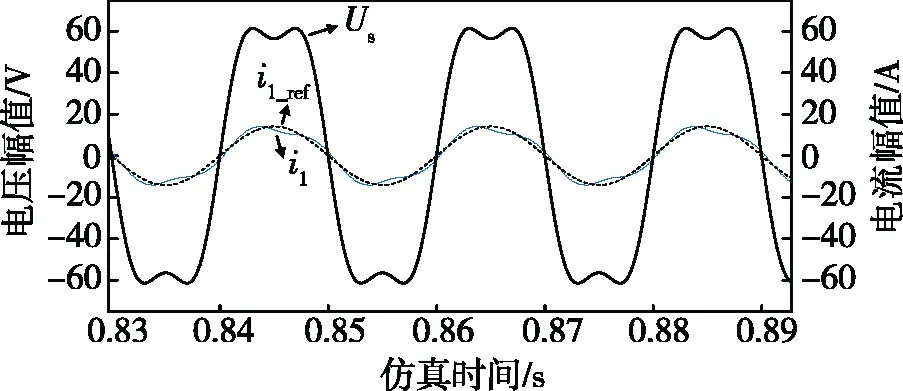
图10 未加入滤波控制时的稳态电网电压和电流。
将本文改进控制策略应用于系统后,网侧电流如图11所示。加入谐波补偿控制后参考电流中的谐波成分已被滤除,网侧电流接近正弦波形,取得了良好的控制效果。
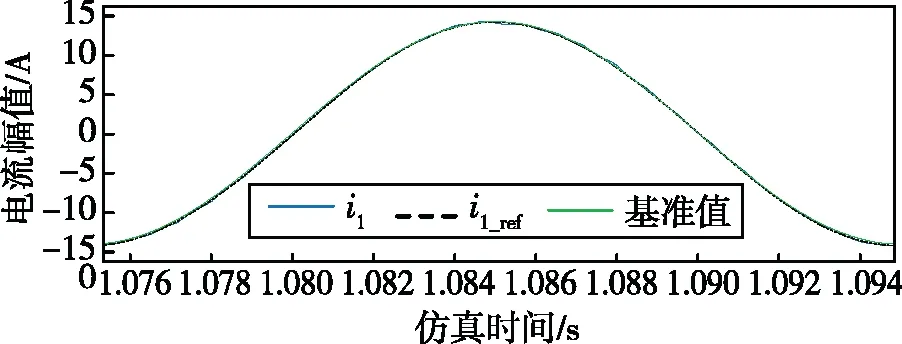
图11 加入改进控制策略的稳态电流。
对稳定后的i1进行傅里叶分解及谐波分析,得到图12所示对比结果。经计算,在网侧电流i1中,采用改进控制策略后,电流谐波总畸变率从19.96%下降到1.70%,表明了本文改进控制策略的有效性。
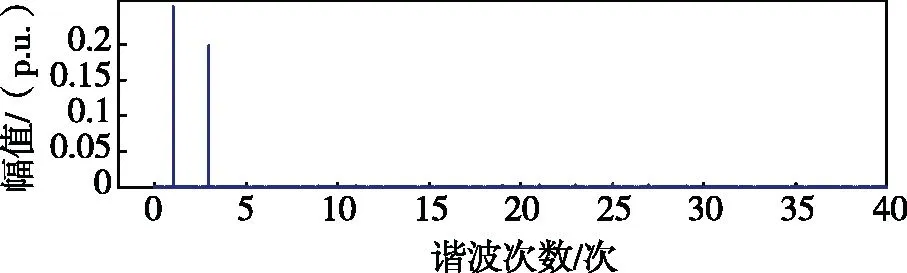
(a)改进策略前的电网侧电流谐波含量19.96%。
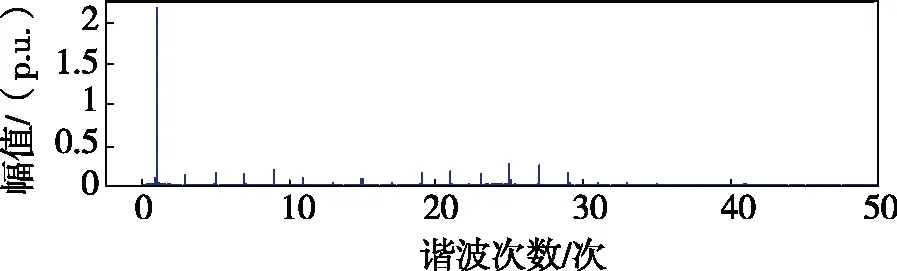
(b)改进策略后的电网侧电流谐波含量1.70%图12 控制策略改进前后的电流FFT对比。
4.2 电压波动时的控制效果分析
为了模拟系统电压发生跌落时的最坏状况,在原系统稳定后,于0.6 s时使系统电压突然跌落至原来的20%。由图13可知,直流侧电压瞬间跌到43 V后开始缓步回升至65 V左右,1.225 s时随着电网电压的回升直流电压激增,最高可达270 V,之后慢慢于1.85 s恢复到稳态的100 V。当系统电压回升的瞬间,参考电流突然升至180 A,网侧实际电流紧接着变大到220 A。可见,电网电压的突然跌落再回升的瞬间,会给系统带来相当大的冲击,影响系统运行安全。
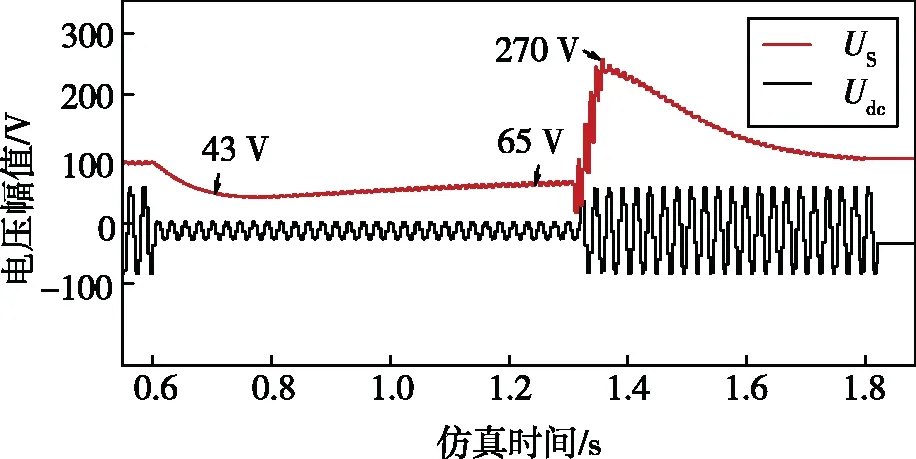
(a)电网电压瞬时跌落。
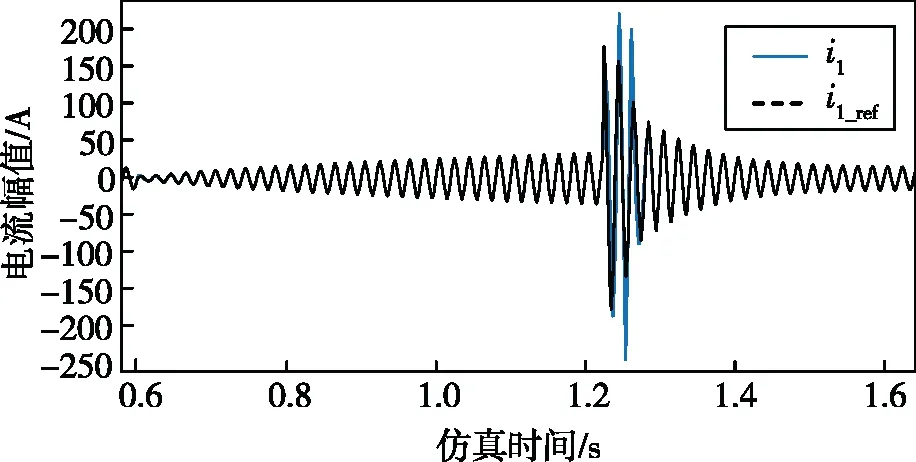
(b)电网电压跌落时的电流变化图13 电网电压瞬时跌落及电流变化情况。
采用本文控制策略后,能够限制参考电流信号的幅值,避免电压剧烈变化时带来的功率冲击。图14中给出了采用本文控制策略后的电网侧电流波形。
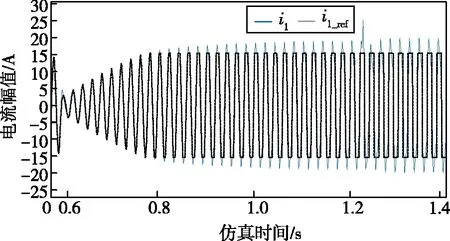
图14 采用改进控制策略后电网电压跌落时的电流。
由图中可以看出,电压跌落时的实际参考电流被严格限制在15.4 A以下,网侧电流峰值也仅达到25 A,较之前的220 A有明显的降低;电压突增时的网侧实际电流最高仅达16.3 A,较之于先前的17 A也有所减小。按照电网严重故障时考虑,其短路冲击电流一般不超过2.55倍次暂态电流。改进控制环后,网侧电流峰值均可以达到上述标准,证明了本文方法的有效性。
5 结 论
构建了含LCL滤波的全桥变流器运行控制数学模型,提出了滤波参数精细化设计方法。通过合理选择总电感值,兼顾了滤波能力、工作效率和动态响应特性。通过采取滤波电容支路串联阻尼电阻的方式,在降低谐振幅值的同时保证了系统稳定性。在LCL滤波器接入后的变流器双环控制策略中,基于PI控制器的电压外环保证了响应速度,基于QPR控制器的电流内环保证了输出精度,并加入了带通滤波和限幅环节降低了运行环境突变的影响。算例分析证明了本文方法在高次谐波抑制、电网电压突降等场景下的有效性和适用性。本文研究为分布式电源并网变流装置的控制参数和控制策略设计提供了手段,为促进分布式能源的高品质并网接入与消纳利用提供了支撑与保障。
