一种内蕴基线漂移校正的人工地震波反应谱拟合方法
2023-10-18张树翠夏宏升张欣刚姚文莉齐朝晖刘大强
张树翠, 夏宏升, 张欣刚,, 姚文莉, 齐朝晖, 刘大强
(1. 青岛理工大学理学院, 山东 青岛 266525; 2. 上海中联重科桩工机械有限公司, 上海 201613;3. 工业装备结构分析国家重点实验室, 辽宁 大连 116024;4. 大连华锐重工集团股份有限公司, 辽宁 大连 116022)
0 引言
拟合匹配目标反应谱的人工地震波是开展重大工程结构非线性时程分析的重要依据之一[1],特别是在对核电楼层反应谱进行拟合时,其“峰多谷深”的特点进一步增大了收敛难度[2-3]。因此,快速高精度拟合真实、合理且匹配目标反应谱的人工地震动仍然面临很大的挑战[4]。
目前相关地震动模拟方法主要有时域法和频域法[5]。以三角级数法[6-7]等为代表的频域方法能够保留初始地震动的相位谱[8],且不需要以自然波作为必须条件,因此仍然具有时域方法不可替代的作用。为了提高人工波拟合效率,李建波等[9]提出了一种人工波初筛策略来避免迭代过程陷入某些特定随机状况。由于这些拟合算法仅考虑了加速度时程的非平稳性特征,且较少考虑其对速度、位移时程的影响[10],因此在通过两次积分得到速度、位移时程曲线后还需采用基线校正[11]的手段来消除基线漂移问题。陈三红等[12]提出在每次迭代时都对所得加速度时程进行基线校正处理,从而避免了时程积分时的基线漂移。Hancock等[13]通过调整小波函数消除了速度和位移时程的漂移,但无法得到封闭的小波系数解。LA Atik等[14]提出了不含位移和速度时程漂移的调整小波函数来得到小波系数的封闭解。张郁山等[15]构造了一种用于校正的增量加速度小波函数,采用该函数积分得到的增量速度和增量位移曲线不出现基线漂移。王体强等[16]提出一种自适应鲁棒加速度积分方法并进行可靠度分析,该文献综述了10种代表性的加速度积分方法,例如周宝峰等[17]提出的基于Hermit插值和平坦度为判据的加速度积分方法,以及被美国地质调查局(United States Geological Survey,USGS)采用的USGS法[18]等,并对各算法的基线校正原理和特点进行了总结评述。
上述研究的共同特点是:在获得加速度时程后通常需要进行基线校正处理才能消除位移、速度时程中的基线漂移问题。 既然基线漂移问题在拟合完成后也要被消除,那么如何在拟合过程中就使其自然满足基线归零条件是非常值得研究的课题。
结合该研究思路,提出一种内蕴基线漂移校正且匹配目标反应谱的人工地震波直接拟合方法。该方法采用与传统频域法相反的思路:首先构造非平稳位移时程表达式,其次求导得到速度与加速度时程表达式,进一步确定使其同时满足归零条件的包络函数,随后利用单自由度系统谐波响应解析式将目标反应谱匹配问题转化为与之等价的非线性方程组,利用高效的非线性方程求解算法快速迭代期望幅值,对随机相位谱的修正来进一步提高拟合精度,最终同时给出满足归零条件的位移、速度及加速度时程。数值算例验证了所提方法的拟合效率和精度。
1 频域法拟合人工地震波
采用三角级数法拟合人工地震波,并对幅值谱进行迭代使其匹配目标反应谱。该过程简述如下:
(1) 利用一组具有随机相位的三角函数构造近似高斯平稳随机过程:
(1)
式中:Ck为傅里叶幅值谱;φk为随机相位谱;a(t)是具有零均值和(单边)功率谱密度函数的高斯平稳随机过程。傅里叶幅值谱可表示为:
(2)
式中:S(ωk)为功率谱密度函数;Δω为频域采样间隔。
标准加速度反应谱与功率谱密度函数的关系为:
(3)

(2) 将平稳随机过程和考虑非平稳特性的外包线函数做乘积:
(4)
(5)
(6)

2 内蕴基线校正的直接拟合方法
为使加速度、速度及位移时程自然满足归零条件,提出一种与传统频域法相反的思路,将非平稳的位移时程u(t)表示为:
(7)
式中各参数的意义与式(4)一致。对上式求两次时间导数,得到:
(8)
(9)
为了使位移、速度与加速度时程自然满足归零条件,可构造在上升段、平稳段以及衰减段平滑过渡的包络函数,例如:式(7)~式(9)中的强度包络函数f(t)应当具备或满足如下条件:(1) 在起始和终止时刻保证位移、速度及加速度函数值为0;(2) 在平稳段包络函数值为1;(3) 在平稳段的开始和结束时刻应当具备二阶连续性。 亦即满足如下条件:
(10)
为满足上述光滑条件,在上升段和衰减段,强度包络函数可以由5次多项式进行表示:
(11)
将式(11)代入式(10)可得:
(12)
(13)
式中:m=T-t2。由此可以解出式(11)中的待定系数,由此得到的包络函数为光滑的连续函数。强度包络函数的选择不唯一,例如式(5)给出的经典包络函数也可以作为式(7)~(9)中的包络函数。
结合上述条件,加速度时程函数式(9)在平稳段的表达式可写为:
(14)

为求解人工地震波反应谱引入如下假设:单自由度系统在人工地震波作用下的最大地震响应发生在强震阶段,故可由式(14)求解其最大地震响应,进而获得人工地震波反应谱。
依据式(14),可将圆频率为ωj的单自由度系统谐波响应表达式写为:
(15)
式中:ξ为单自由度系统阻尼比:ωj为第j个单自由度系统的圆频率。
求出式(15)的复数解可得到单自由度系统的相对位移解xj为:
(16)
(17)
(18)

(19)
式中:符号“Imag”表示对复数取虚部。
依据反应谱纵轴的意义,拟合设计反应谱的目标是使下式成立:
(20)
(21)

至此,就可将以匹配目标反应谱的人工地震波拟合问题转化为求解一组以待求幅值谱为迭代目标的非线性方程组[式(20)~(21)]。利用成熟高效的非线性方程求解器,例如MATLAB “fsolve”求解器可快速迭代满足要求的幅值谱Ak。
上述人工波拟合算法的流程如图1所示。所提算法具有如下优势:

图1 人工波拟合流程图Fig.1 Flow diagram for artificial seismic wave fitting
(1) 能够快速拟合自然满足基线归零条件的人工地震波,直接得到位移、速度以及加速度时程;
(2) 不必在得到加速度时程后再构造基线校正算法处理基线漂移问题;
(3) 将匹配目标反应谱的拟合问题转化为以待求幅值谱为迭代目标的非线性方程,结合高效的非线性方程求解器进行求解,具有编程难度低,收敛精度高的特点,可成为人工波拟合的新途径。
3 反应谱拟合算例
为验证所提人工地震波拟合方法的有效性,选择核电站抗震设计中的Rg1.60标准谱、某核岛内41.68 m高度的水平、竖向楼层谱以及《建筑抗震设计规范(GB 50011—2010)》中的设计谱分别作为目标反应谱,并对分析结果的拟合精度、迭代残差以及拟合效率进行分析。
采用MATLAB “fsolve”求解器进行迭代时,对最大迭代步数“MaxIterations”进行限制以提高迭代效率。具体迭代步骤如下:首先仍然依据标准加速度反应谱与功率谱密度函数的近似关系得到一组幅值谱作为迭代初值带入求解器迭代15次;随后以相位谱为目标迭代3次;最后再以幅值谱为目标迭代7次。由于所提方法与考虑迭代相关的拟合方法不同,因此不开展两者之间的精度对比。
表1给出了拟合精度和收敛耗时情况,图2给出了3组随机相位谱下采用Rg1.60标准谱拟合的人工波反应谱,图2(d)~(f)给出了非线性方程求解器迭代过程中的迭代残差趋势。
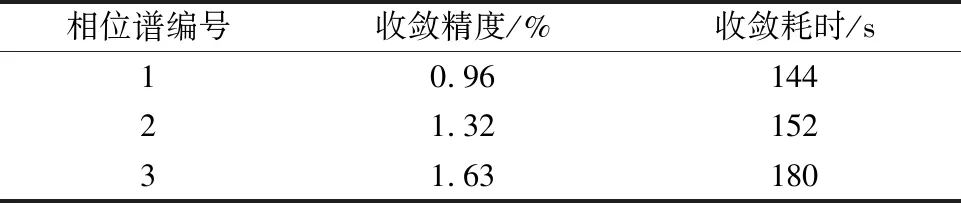
表1 精度与效率比较

图2 Rg1.60目标谱拟合结果Fig.2 Fitting results of Rg1.60 target spectrum
由表1可知,所提方法对于3组随机相位谱均能达到3%以内的高精度要求(70个拟合点),且收敛时间均在5 min以内。在精度和效率方面都达到了预期的拟合要求。
分析图2结果可见,图2(a)中第10个迭代步已达到较好的收敛精度。而图2(b)结果则显示,在对随机相位谱进行修正后,继续对幅值谱进行迭代也达到了预期的精度效果。图2(c)中的结果表明在最后几个迭代步达到收敛精度。所提算法在3组随机相位谱下均达到理想的拟合效果。
从拟合难度来看,Rg1.60反应谱幅值呈线性分布,拟合效果较好。为了验证所提方法能够处理目标曲线更为复杂的反应谱拟合问题的能力,采用相对复杂的核电厂楼层谱,采用3组随机相位谱,所得结果如图3所示(RRS表示目标反应谱)。核电厂楼层谱曲线在局部具有诸多复杂的“转折”之处,本文选择50~60个目标点进行拟合,目标曲线“转折”的细节有所弱化。图中结果可见,对于核电厂楼层谱,所提方法在20个迭代步内达到合理的拟合效果。特别是在核厂房基础结构放大效果的影响下,2%、5%阻尼比的水平方向楼层谱的峰值可达6g~10g,因此在相应的频段采用加密的频率点参与拟合后可进一步提高求解器的收敛效果。
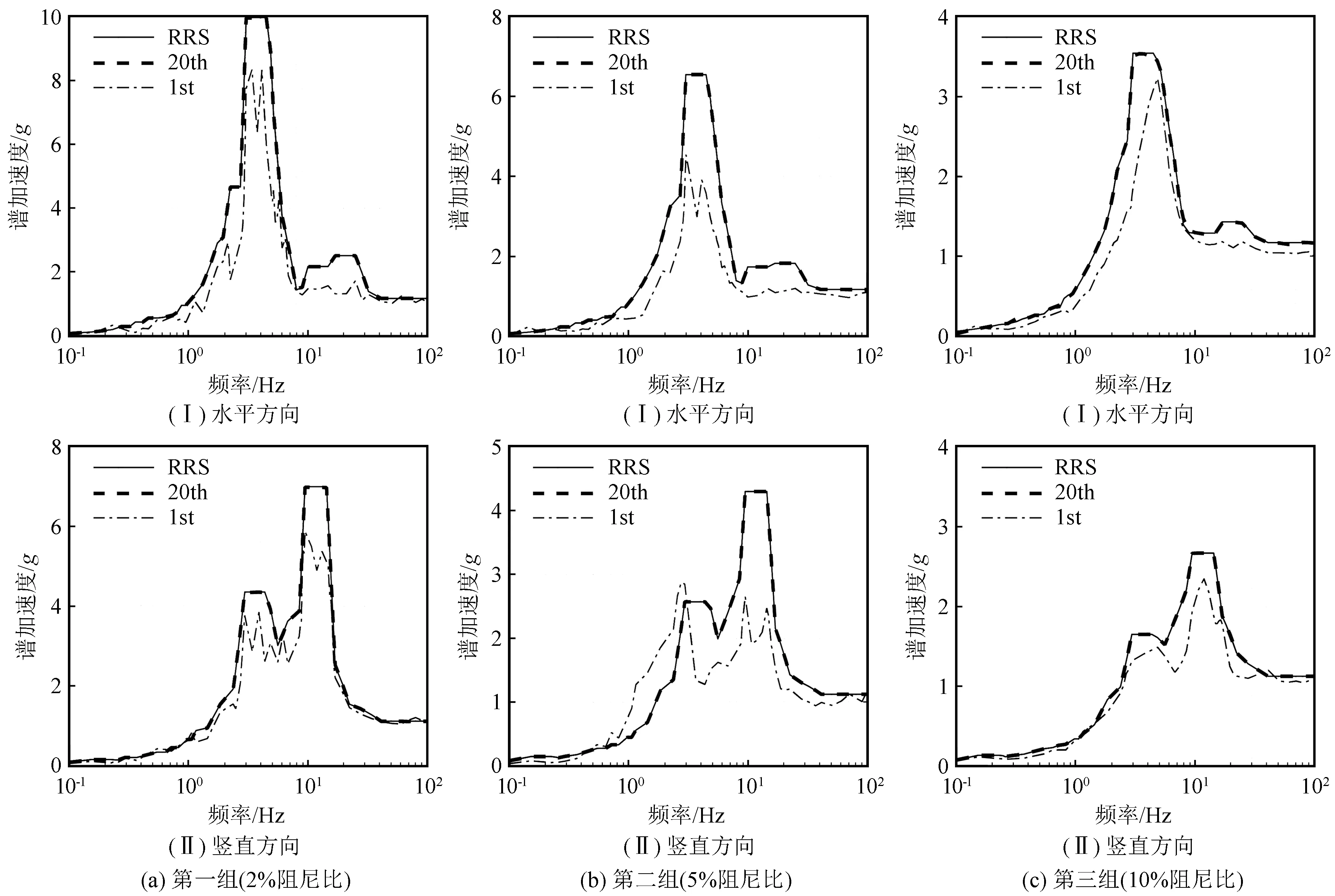
图3 核电厂楼层谱拟合结果Fig.3 Fitting results of floor spectrum of nuclear power plant
进一步分析不同阻尼比下的拟合结果:采用相同的傅里叶幅值谱初值条件时,2%和10%阻尼比下的拟合效率要比5%阻尼比要高,其原因尚不明确。同时还需说明的是,图中所示目标反应谱的拟合点数目均在50~60之间,与原反应谱相比复杂程度有所降低。若要充分考虑原反应谱的细节,则拟合点的数目将显著增大,顽固点相应增多,所提方法的拟合能力需要后续进一步的检验和优化。另一方面,图3采用的核电楼层谱虽然局部细节复杂,但仅有两个“高峰”,尚不能完全体现“峰多谷深”的特点,后续将开展进一步的相关研究。
最后,采用《建筑抗震设计规范(GB 50011—2010)》规定的反应谱进行拟合,参数为:设防烈度8度,Ⅰ类场地,设计地震分组为2组,特征周期Tg=0.2 s,地震影响系数取αmax=1.06。
图4同样给出了3组随机相位谱下的拟合结果对比。图中每一列对应一组相同的随机相位谱,图4(d)~(f)为高频部分的局部细节图,图4(g)~(i)对应低频部分的局部细节图。

图4 3组随机相位谱拟合结果对比Fig.4 Comparison between fitting results of three groups of random phase spectra
由于拟合点的分布较为复杂,因此第一次迭代次数调整为30次,后两次迭代次数不变。分析结果表明,初次迭代时人工波反应谱和目标反应谱差距较大,但很快趋近目标值。第一次迭代结束时,第一组的高频段末端仍存在误差为4%的顽固点,随后在对相位谱进行5次迭代调整后,顽固点的相对误差迅速降低到0.82%,达到了较好的收敛效果。
在高频段,单自由度系统的地震响应近乎刚体运动,一些学者发现采用传统频域法在一些特定情况下有时面临拟合困难的问题[4]。例如对核电站楼层谱进行拟合时,25~100 Hz的频率段就存在大量的顽固点。所提方法依据单自由度系统谐波响应的解析解,同时采用成熟的非线性方程求解器并结合高效的L-M算法进行迭代,在低频和高频段都得到了较好的收敛精度。
图5给出了采用所提方法得到的人工地震波加速度、速度以及位移时程。由于算法内蕴基线归零条件,因此各时程曲线均不存在基线漂移问题。
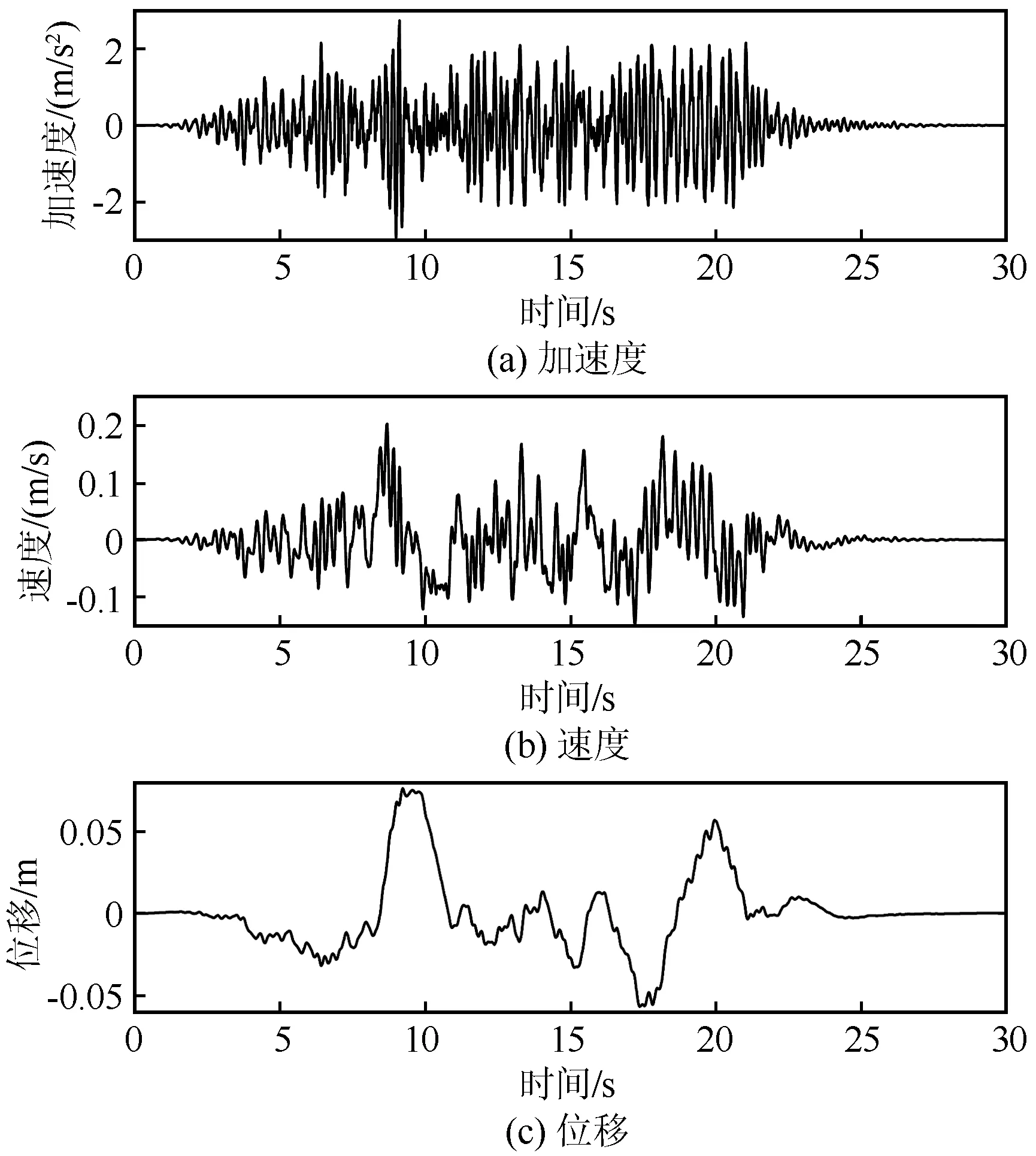
图5 基线归零的人工地震波时程Fig.5 Time history of artificial seismic wave with zero baseline
4 结论
在传统频域法的基础上提出一种人工地震波反应谱直接拟合方法,采用多组设计反应谱验证了所提方法的匹配精度。本方法内蕴基线归零条件,将匹配目标反应谱问题转化为以幅值谱为目标的非线性方程进行快速迭代求解,具有编程友好、收敛精度高的特点。总结本文可得如下结论:
(1) 所提方法以求导代替积分为总体思路,在快速拟合算法中内蕴基线归零条件,能够同时给出满足归零条件的位移、速度和加速度时程,避免了传统方法加速度积分过程中的基线漂移问题。
(2) 以单自由度系统谐波响应解析解为依据,将匹配目标谱的人工地震波拟合问题转化为以待求幅值谱为变量的非线性方程组。采用高效的非线性方程求解器进行迭代,具有收敛速度快,低频、高频段拟合精度高的优势。
(3) 考虑了相位谱进行综合迭代,匹配效率和匹配精度进一步提高。所提算法编程难度低,且不必构造复杂的迭代格式。
(4) 核电楼层谱呈现宏观“峰多谷深”、局部“转折”细节较多的特点,对高精度人工波拟合提出了更高的挑战。因此,所提算法对复杂楼层谱的拟合能力需要进一步改进和优化,同时也需要给出筛选判据,有效排除理论上难以匹配目标反应谱的人工地震波,提高整体拟合效率。
