一种联合深度神经网络的公共空间人员总体舒适度计算方法
2023-10-18陆剑峰
夏 飞,闻 卫,袁 博,夏 麟,张 浩,陆剑峰
1(上海电力大学 自动化工程学院,上海 200090) 2(南瑞集团(国网电力科学研究院)有限公司,南京 210000) 3(华建数创(上海)科技有限公司,上海200070) 4(同济大学 电子与信息工程学院,上海 201804)
1 引 言
我国建筑能耗占全国能源消耗总量的20.62%左右,公共建筑的能耗占整个建筑能耗的37.71%.其中办公建筑空调能耗占据建筑总能耗的55%左右,是占比最高的一项[1].目前空调能耗系统智能化控制的重点在于能耗的调节,而对于室内人员舒适度考虑得较少.科学合理的空调用电管控手段,应当将建筑运行节能与人的舒适度综合考虑,既要满足人的舒适性需要,又要避免能源的过度浪费[2].
目前针对室内人员舒适度判别的研究,主要集中于针对热环境的研究.自Fanger[3]提出预测平均指标PMV(Predicted Mean Vote)后,PMV就成为了国际公认的热感觉评价指标,因为该指标考虑到了与人体相关的诸多因素.虽然该指标虽考虑全面,但相关数据获取需要通过实验的方式进行记录,给实际工程应用带来难度.近年研究对于如何更高效地获得参数却没有很好的解决方法.为了规避参数间复杂的非线性关系,通常将人员的服装热阻值使用经验值替代,如取夏季工况下人员的服装热阻为0.5,冬季工况下为0.9,忽略了服装热阻对人体舒适度的影响.使用这样的模型评价公共空间人员总体舒适度,存在一定的局限性.即使在实验中,这些模型通常使用一位实验人员的服装热阻值,计算PMV指标,用于评价当前环境中人员的舒适度.但在实际情况中,不同人员的衣着情况是不同的,用一个人员的PMV值评价整个室内人员的舒适度并不准确.本文认为,应该根据每个人的服装热阻,逐一计算出对应的PMV值,最终得到平均PMV值,从而更加全面反映室内人员总体的舒适度情况.考虑到PMV的计算复杂,这就更需要借助于智能检测设备与方法,实现指标计算参数的获取,一方面可以降低工作量,一方面为工程化带来可能.
为了在实际空调用电管理中应用舒适度指标,除了需要实现PMV的智能计算外,还需要采用智能算法对其参数和指标之间的关系进行学习,实现对舒适度的预测.目前研究人员常采用的室内人员舒适度预测模型,包括模糊自适应和神经网络的方法.罗一凡[4]提出了一种基于模糊自适应的热舒适度判别建模方法.由于模糊理论是线性的建模方式,但室内环境等参数都具有时序性,这就导致基于模糊理论建立的模型在评价人体舒适度时有较大的偏差,而神经网络可以以任意的精度逼近非线性问题的解,因此成为了人体舒适度计算方法的主要研究方向.王玉山[5]等人基于BP神经网络建立了人体舒适度评价预测模型,该模型需要用户手动输入活动状态,且十分依赖BP神经网络的权值和阈值的选取.翁虎[6]等人利用DE-BP神经网络建立了室内热舒适度评价模型,但在输入参数选取中忽略了风速和平均辐射度.赵敏华[7]等人提出将粒子群结合BP神经网络进行优化;魏东[8]等人则提出加入遗传算法对BP神经网络进行优化,但这两种算法的局部寻优能力较差.王晓辉[9]等人为了增强遗传算法的局部寻优能力,采用遗传模拟退火算法对BP神经网络进行了优化,但网络仅将温度、风速度和湿度作为模型的输入,仅通过这3个参数来预测PMV值并不全面.同时,由于室内温、湿度等数据具有时间序列特征,而服装热阻又受这些数据的影响,因此用于预测人体舒适度的数据具有明显的时序性.上文所述常用于预测PMV的神经网络并不能很好地处理这样的数据.因此引入能够处理时序性更强的神经网络,将会增加PMV预测的准确性,从而更好地根据舒适度进行空调管控.
综合前文的分析,目前舒适度预测的问题在于:1)计算舒适度的参数不易获取;2)预测模型采用一位人员的舒适度值来评价全体人员的舒适度;3)需要采用时序性处理能力更强的预测模型.如果能够结合物联网,自动获取舒适度计算参数,并采用智能算法建立包含室内所有人员人体参数的舒适度模型,并进一步考虑参数的时间序列特征,得到室内人员的舒适度指数将具有现实意义.因此,本文提出了一种基于图像信息的公共空间人员总体舒适度计算方法.
本文为解决上述问题,提出方法的创新点如下:
1)采用图像识别的方法,智能获取室内人员数量、衣着和冷热状态等个体参数;
2)通过改进Faster R-CNN网络,使之满足室内人员及其不同状态下的多尺度检测需求;
3)提出了一种联合深度学习神经网络的方法,计算室内人员总体舒适度.
在采集到室内人员图像后,针对场景图像中人员大小不一的问题,本文在Faster R-CNN的网络架构上加入了改进后的特征金字塔网络(Feature Pyramid Network,FPN),使用该网络得到室内不同尺度人员的数量,同时对人员的衣着、冷热状态及对应的数量进行识别,将结果与环境参数结合,输入到长短期记忆网络(Long Short-Term Memory,LSTM)建立的舒适度模型,得到更符合人员总体评价的舒适度指数.本文选择的LSTM神经网络不仅继承了RNN可有效处理具有时序性的数据这一优点,且还克服了梯度消失的问题.因此本文使用LSTM神经网络进行舒适度预测,能够更好地学习到输入参数与舒适度之间的依赖信息,其内部的反馈连接更适合处理PMV指标与参数之间的复杂非线性关系,具有更强的可靠性.

图1 舒适度计算方法框图Fig.1 Block diagram of comfort calculation method
本文提出方法的总体框图如图1所示.
2 人员及状态的深度网络识别模型
为了进行人员舒适度评价,需要采集相关参数,包括人员数量和人员衣着、冷热状态的数量,以及室内温度和湿度等相关信息.本文除了应用温、湿度传感器采集数据外,采用室内摄像头的视频信息,通过多尺度特征网络实现人员的识别.在训练模型时,将人员冷热及人员衣着状态特征一同送入网络训练,得到可以同时完成人员数量和人员衣着、冷热状态数量识别的模型.
目前针对目标识别的研究,可分为传统的方法和基于深度学习的方法.在传统目标检测的算法中,特征提取是其核心,由于人体的类间相似性较高[10],且受到视觉角度和位置等因素的影响,在人员较密集时会产生遮挡问题[11].使用人工提取特征的方法不仅难以提取有效的特征,且难度较大,最终导致人员识别率低下[12].如果要在人员数量识别的基础上,进一步实现衣着和冷热的识别就更加困难.而针对人员衣着识别的方法主要有两种:1)先进行衣着分割,然后进行衣着区域识别;2)方法是利用姿态估计模型获取人体姿态位置[13],通过位姿得到衣着位置,再用阈值划分算法对衣着进行特征判断.这些方法的局限性在于,需要检测到人脸或人体躯干后,才能对人体的衣着进行识别,且两种方法都默认衣着是纯色的.
基于以上分析,本文选择基于深度学习的方法进行人体及状态识别.深度学习方法又可被分为检测实时性高的One-Stage和检测精度更高的Two-Stage[14].考虑到在进行人体舒适度判断时并不要求实时性,但需要较高的准确度,因此本文选择了Two-Stage网络中准确度较高Faster R-CNN,在其基础上加入改进的FPN,同时改变了锚框尺度来进一步提高算法检测的准确率.改进后的Faster R-CNN算法模型如图1中深度网络识别模型部分所示.首先通过ResNet50的预处理,得到C1后经过4个卷积模块,生成特征图{C2,C3,C4,C5}.然后将特征图作为输入送到改进后的FPN中,生成不同尺度的{N2,N3,N4,N5,N6}.接着,使用K-Means聚类方法使区域建议网络生成的锚框适用于人体目标,通过Softmax判断锚框中的是否为目标,并对锚框修正,得到较精确的候选区域.Roi Pooling层利用候选区域和多尺度特征[15],得到固定大小的特征图,然后经过全连接操作后,送入Softmax判断目标的类别,通过边界回归得到检测框的位置.
2.1 Faster R-CNN网络结构的改进
传统FPN利用自顶向下的连接路径[16],对底层特征图的位置信息进行了融合.由于高层特征在经过上采样处理后会损失部分语义信息,使小目标人体特征无法被充分提取,出现漏检情况[17].因此本文在FPN的基础上对原有的特征结构进行了改进,利用各卷积层的特征图,获得不同的特性.其中高卷积层被用于检测大目标物体,而低卷积层因其高分辨率,适用于检测较小的目标.
FPN将ResNet50输出的{C2,C3,C4,C5}作为网络的输入,特征图C5经过1×1卷积后得到T5,以同样的方法对C3、C4、C5进行处理,得到特征图{T2,T3,T4,T5},T2经过1×1卷积得到D2,再经过3×3卷积块处理后得到N2,与此同时对D2进行下采样处理.
(1)
其中,m为输出特征图Di的大小;n为输入图片的大小;p表示padding,为填充像素的大小;f表示filter,为卷积核的大小;s表示strides,为滑动步长.对D2下采样后,与T3卷积后的结果进行张量相加,得到D3,D3经过3×3卷积块处理后得到N3.以同样的方式处理特征图D4和D5,得到特征图{N2,N3,N4,N5},并对N5进行最大池化操作,得到尺寸更小,信息更丰富的特征图N6.改进后的结构如图2所示.

图2 改进后的FPN结构图Fig.2 Improved FPN structure
2.2 锚框尺寸自适应聚类
Faster R-CNN采用了3种尺度以及3种长宽比,即9种不同尺寸的候选框,完成前景区域的提取[18].但由于这些锚框的尺度是基于VOC和COCO等数据集中的类别设置的,对于本文所用的针对室内办公场景下的数据集并不适用.在本文的数据集中,人体在图像画面中所占像素大小不一,因此本文使用了K-Means聚类方法生成适用于室内办公场景下的锚框尺寸.
将人员目标框的真实值作为样本,根据不同样本之间的欧式距离,把距离近的样本归为一类,共划分为k类,用{M1,M2,…Mk}表示.采用误差平方和作为目标函数,如式(2)所示:
(2)
式中x为样本,j=1,2,…,k,是第j个聚类中心.
通过读取图像对应的标签文件中的矩形框坐标值xmin、xmax、ymin、ymax获得人体的长宽分布,按训练比例尺度缩放后对分布情况进行聚类,最终获得9个适用于室内人员识别的锚框尺度和新的锚框长宽比.
3 基于LSTM神经网络的舒适度计算
在诸多影响室内环境的因素中,环境的温度和湿度与人体切身感受密切相关.因此本文在建立人员总体舒适度计算模型时,除了将前文通过图像识别获得的冷热、衣着状态作为人体相关数据,同时选取了室内环境因素作为输入参数.本文通过人体相关参数和环境参数得到人员个体的PMV,再计算平均值作为实际环境下的整体舒适度,以此为依据建立了基于LSTM神经网络的人员总体舒适度计算模型.
3.1 基于PMV的人员总体舒适度计算方法
PMV指标采用了7级标尺[19],从+3~-3分别表示热(+3)、暖(+2)、微暖(+1)、适中(0)、微凉(-1)、凉(-2)、冷(-3).
指标受到空气温度(ta)、空气相对湿度(φ)、空气流动速度(va)、平均辐射温度(tr)这4个环境变量,同时受到人体代谢率(M)和衣服热阻(Icl)这两个人体相关变量的影响.可用式(3)表示:
PMV=f(ta,φ,va,tr,Icl,M)
(3)
根据实际情况,即室内处于无风状态(va=0m/s),参与实验的人员都处于静坐状态,取人体代谢率M=58.2W/m2.因此其数学模型可简化为式(4):

(4)
其中:
tcl=34.07-Icl{3.96×108×fcl[(tcl+273)4]-
(tr+273)4+fclhc(tcl-ta)}
(5)
hc=2.38(tcl-ta)0.25
(6)
(7)
Pa=φ×e[16.653-4030.183/(ta+235)]
(8)
式(4)~式(8)中,ta为空气温度(℃);Pa为人体周围水蒸气压(Pa);fcl为服装表面积系数;tcl为服装表面温度(℃);tr为平均辐射温度(℃);hc为对流传热系数(W/(m2·K));Icl为服装热阻(clo);va为空气流动速度(m/s);φ为空气相对湿度(%).在这些参数中,室内温度、相对湿度可由测量仪测得[20].由于进行实验时为夏季,因此人员的衣着状态分为两类,当衣着为长袖时,取服装热阻Icl=0.61col;当衣着为短袖时,取Icl=0.61col.通过测量得到室内温(ta)、相对湿度(φ),由于室内处于无风状态[21],因此平均辐射温度(tr)=室内温度(ta).将这些参数输入PMV计算工具,得到实验进行时的PMV值.
3.2 基于LSTM的人员总体舒适度预测模型
LSTM神经网络由LSTM记忆块组成,记忆细胞和门构成了这些记忆块[22].本文使用的是由输入门(It)、输出门(Ot)以及遗忘门(Ft)组成的最基本的LSTM网络,如图3所示.

图3 LSTM单元结构Fig.3 LSTM unit structure
3个门的计算公式如式(9)~式(15)所示.
It=σ(XtUi+Ht-1Wi+bi)
(9)
Ot=σ(XtUo+Ht-1Wo+bo)
(10)
Ft=σ(XtUf+Ht-1Wf+bf)
(11)
Gt=tanh(UgXt+Ht-1Wg+bg)
(12)
Ct=Ft⊗Ct-1+It⊗Gt
(13)
Ht=Ot⊗tanh(Ct)
(14)
式中,U和W为权重,b为偏置向量,σ表示激活函数Sigmoid[23],其表达式为:
(15)
确定LSTM神经网络结构后,将人员参数和环境参数作为神经网络的输入,人员总体舒适度作为输出,训练得到一个多输入、单输出的模型.
4 实验结果分析
本文实验环境搭建于某公共会议室内,硬件配置包括视频采集设备一套、笔记本一台.笔记本的操作系统为macOS系统,CPU频率3.2GHz,内存8G.视频采集设备为通用网络摄像机,采用了200万像素CMOS图像传感器.网络摄像头安装后,使视频采集区域尽量覆盖了整个室内场景.采集的图像通过网络传输到笔记本电脑进行识别和分析.图像识别程序在Python 3.7编程环境下进行开发.
4.1 人员数量和状态识别结果分析
本文通过网络摄像头采集了大量会议室场景下的人员图像组成本文的数据集,为获得更多的样本数量,本文在不同时间进行了多次相同的实验,得到1000张图片的样本数据用以模型的训练.本文建立的深度识别网络中的残差网络ResNet50能够自动地从尺寸不同的图片中提取出特征,因此不需要改变数据集的尺寸,直接采用LabelImg标注工具,按照VOC格式对人体的不同衣着、冷热状态进行标注,获得每个图像中不同标签的矩阵.标注后将数据集按照7∶2∶1的比例划分为训练集、测试集与验证集.其中训练集用于训练模型的各项参数,测试集用于评估模型的泛化能力,验证集用于优化训练过程中模型的参数.模型训练结束后,通过各项性能评价指标来衡量模型性能.
对于人员识别的模型,本文采用AP作为模型性能评价的指标.AP表示测试集中某一类别的平均准确率,准确率P代表了一个类别在一幅图中被模型正确识别的个数,准确率的计算如式(16)所示:
(16)
其中TP为预测正确的样本数;FP为预测错误的样本数.
AP的计算如式(17)所示:
(17)
式(17)中,c为测试集图片数量;k为测试集中第k张图像;Pk为第k张图像中某一类别的准确率.
4.1.1 人员数量识别结果及分析
本文在模型训练时,考虑到数据集的体量并不大,因此采用随机梯度下降法作为优化器进行训练,加快训练过程.设置学习率为0.005,训练时采用线性增加策略,使学习率从初始的0.00199通过迭代逐渐增加至0.005,权值衰减系数为0.0001,epoch设置为150,迭代次数为1000次,每迭代一个epoch保存一次模型,最后选择精度最高的模型进行保留.
训练完成后,应用本文提出的改进算法建立人员数量识别模型,并应用验证集对模型性能进行了测试.为了说明本文提出方法的优越性,对改进方法前后的效果进行了比较.在本文实验场景中,需要识别的人数为26人.
分别使用Faster R-CNN算法和本文提出的改进算法模型进行了人员识别,结果如图4所示.

图4 改进前后Faster R-CNN的人员识别效果Fig.4 Personnel identification effect of Faster R-CNN before and after improvement
在图4中,出现误检的是采用Faster R-CNN进行人员识别的结果.可以看到左上角的检测结果中,一个目标被多个检测框圈出的情况,即出现了误检.在右上角的检测结果中,有人员目标未被框出,即发生了漏检.左下角与右下角的是使用改进后算法进行检测的结果,可以看到,人员识别的误检、漏检问题得到了改善.为进一步说明本文方法的效果,将Faster R-CNN算法,和其只改进锚框的算法,只改进FPN的算法及同时改进锚框和FPN的算法,即本文提出的改进Faster R-CNN算法进行了比较,实验结果如表1所示.

表1 人员数量识别结果Table 1 Result of personnel identification
从表1可以看出,当仅对锚框尺寸进行自适应聚类后,AP从Faster R-CNN算法识别的67.23%提高到了改进锚框算法后的72.07%,而仅改进FPN算法的AP则提高到了80.68%.当对两者同时进行改进时,模型进行人员识别时,其AP提高到了85.46%.由此可见,本文提出的算法在人员识别中性能提升最大.
为进一步说明本文算法的优越性,本文选择了YOLOV3与YOLOV4进行了人员数量的识别,模型算法识别结果如表2所示.

表2 YOLOV3与YOLOV4人员数量识别结果Table 2 Result of personnel identification based on YOLOV3 and YOLOV4
从表2中可以看出,本文提出的算法比YOLOV3算法和YOLOV4算法,分别在准确性上提高了22个百分数和近34个百分数.
4.1.2 人员数量识别结果及分析
接下来,和4.1.1小节类似,比较了Faster R-CNN的几种改进方法,在人员衣着识别上的效果,模型的具体效果如表3所示.

表3 人员衣着状态识别结果Table 3 Result of personnel clothing identification
当只进行锚框自适应聚类,识别人员T恤和衬衫时算法的AP仅有小幅度的提升.只改进FPN后的算法,在识别人员T恤和衬衫时,AP分别提升了13.99%和10.25%.当使用本文提出的改进算法进行人员T恤和衬衫识别时,AP分别提高了15.3%和17.23%,可见本文算法在人员衣着识别的应用中具有较好的效果.
4.1.3 人员冷热状态识别结果及分析
同样地,分别用Faster R-CNN、只进行锚框自适应聚类的Faster R-CNN、只改进FPN的Faster R-CNN以及本文提出的算法,建立了人员冷热状态识别模型.4个模型的识别结果如表4所示.

表4 人员冷热状态识别结果Table 4 Result of personnel hot and cold status identification
从表4中可以看到,进行锚框自适应聚类后,Faster R-CNN在冷、热识别中,算法的AP分别提高了1.19%和17.09%.使用改进FPN后的算法进行冷、热识别时,AP分别提高了15.52%和19.74%,而本文所提算法具有最大的提升效果,AP分别提高了21.54%和26.88%,在进行人员冷热状态识别中有较好的性能.
4.2 人员舒适度计算实验及结果分析
4.2.1 人员舒适度预测模型数据集建立
构建人员总体舒适度模型,需要先建立数据集.本文的实验场景为某公共会议室内.为了获得建立数据集所需样本,在不同时间进行了多次相同的实验,得到305张图片的样本用以模型训练,并通过测量仪表获取每张图片时会议室中的温、湿度.将图片送入前文建立的深度网络识别模型,得到每张图中不同衣着、冷热状态下人员的数量,至此就得到了所有神经网络的输入参数.通过室内温、湿度数据,并根据当日实验人员的衣着、冷热状态数量,逐一计算PMV值,最后取均值作为当时环境下的人员总体舒适度指标.部分样本数据形式如表5所示.其中xi(i=1,2,…,10)分别对应室内温度(x1)、室内人员总数(x2)、穿衬衫人员的数量(x3)、穿T恤人员的数量(x4)、穿卫衣人员的数量(x5)、穿棉衣人员的数量(x6)、状态为舒适的人员数量(x7)、状态为热的人员数量(x8)、状态冷的人员数量(x9)以及室内湿度(x10);Y为人员总体舒适度.
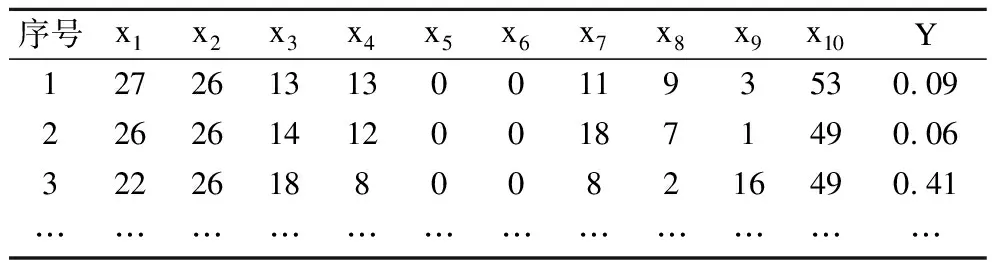
表5 样本数据形式Table 5 Form of sample data
本文采用决定系数R2、均方误差MSE以及平均绝对误差MAE作为评价模型的指标.
决定系数越接近1则表明模型的拟合程度越好,其计算公式如式(18)所示:
(18)
均方误差表示误差平方的平均值,用于体现模型预测效果的稳定性,其值越小,则模型拟合数据的能力越强,公式如式(19)所示:
(19)
平均绝对误差反映的是预测误差的真实情况,其公式如式(20)所示:
(20)
4.2.2 LSTM预测模型训练及结果分析
在样本数据集中随机抽取80%的数据,共244组作为学习样本,剩下20%的数据则作为测试样本.由于输入特征的性质不同,因此为了避免模型受到数值较高的特征影响,因此在训练前首先对数据进行了归一化处理.神经网络的参数设定并无确切的标准,因此需要手动设置结构参数,本文选择了均方误差(MSE)作为损失函数.在实验程序中,还需要选定的参数包括隐含层数量、神经元数量以及学习率.首先将隐含层数量设定为2层,然后在模型训练过程中不断调整神经网络隐含层神经元的数量和学习率,最后根据模型效果确定参数.本文在[100,1000]之间选择了6个神经元分别计算了测试集上的均方误差,结果如图5所示.

图5 不同神经元数量迭代结果Fig.5 Iterative results of different neuron numbers
由图5可以看出,模型训练的迭代次数不变,随着神经元数量的增加,模型的预测效果会有所提升.当神经元数量超过1000时,模型的预测效果提升很小,且由于模型过于复杂,其训练速度大幅降低,不利于在性能较低的设备上使用,因此最终确定神经元数量为1000.在确定学习率时,将取值范围设为[0,0.02],以步长为0.0001遍历该范围内的值,最终确定学习率为0.0024.
综上,本文最终模型的参数设置如表6所示.

表6 模型参数取值Table 6 Model parameter value
通过训练集的训练得到了基于LSTM神经网络的预测模型,并使用测试集获得了模型的性能指标,为了对比模型的效果,本文使用BP、PSO-BP及RBF神经网络对同样的数据集进行训练,得到了4个人员总体舒适度预测模型.
表7为模型在测试集上的性能指标数值.

表7 模型评价指标Table 7 Model evaluation index
从表7中可以看到,基于LSTM神经网络建立的预测模型的决定系数最接近数值1,说明其拟合程度最好.4个模型的均方误差及平均绝对误差都在较小的范围内,但基于BP神经网络建立的模型,其均方误差和平均绝对误差比其他模型高了一个数量级.基于GA-BP与RBF建立的预测模型,都有较好的表现,但基于LSTM建立模型的均方误差比这两个模型小了一个数量级.可见在4个模型中,基于LSTM的预测模型性能最为优异.
为了进一步说明本文建立的模型在预测人员总体舒适度中的优越性,将61个测试样本分别送入4个模型中进行预测,并将模型的预测结果与实际值(通过计算得到的PMV值)进行比较,如图6所示.同时为了更清楚地对比,也为进一步说明本文所建立模型的准确性,分别计算了4个模型预测的绝对误差,误差曲线结果如图6中模型误差曲线所示.
从模型误差曲线中可以看到,基于BP神经网络模型预测的绝对误差在-0.42~0.76之间,使用基于GA-BP建立的模型绝对误差在-0.306~0.42之间,而基于RBF神经网络模型预测的绝对误差处于-0.05~0.05之间,而使用基于LSTM神经网络模型进行预测,绝对误差在-0.03~0.023之间.由上述数据可知,虽然4个模型在评价指标中的数值相差并不大,

图6 模型预测效果Fig.6 Model prediction results
但通过模型预测结果与实际值之间绝对误差的比较可见,本文提出的基于LSTM神经网络建立的预测模型,在人员舒适度计算上有很高的准确性.根据舒适度指标划分,相邻两级舒适度之间的差值为1,因此该范围内的误差对计算人员总体舒适度的影响较小,可见本文提出的方法在预测人员总体舒适度时具有良好的表现.
5 结束语
本文首先对Faster R-CNN进行了改进,提升了模型在识别人员及不同状态时的准确率.同时提出了一种联合深度学习神经网络的方法,可以智能地获取室内人员和不同衣着、不同冷热状态下人员的数量,并由这些参数和室内环境参数组成输入变量,通过LSTM神经网络构建人员舒适度预测模型,得到当前环境中人员总体舒适度指数.模型的平均绝对误差为0.0024,说明模型有较好的预测效果.在后续工作中,可以使用本文所提方法计算人员总体舒适度后,以此为依据进行空调温度控制,在节能的同时满足人体的舒适需求.
