从平均数视角看抽屉原理
2023-10-18王友伟
王友伟
(江苏省南京市金陵中学 210005)
1 抽屉原理的由来
抽屉原理又叫鸽笼原理,是由德国数学家狄利克雷于19世纪初期首先发现的,亦称狄利克雷原理.狄利克雷给出的定义是这样的:“如果有5个鸽子笼,养鸽人养了6只鸽子,那么当鸽子飞回笼中后,有一个笼子中至少装有2只鸽子.”最早狄利克雷运用抽屉原理去解决数论的问题.
2 从平均数视角再解竞赛题
中小学的各类数学竞赛辅导书中对抽屉原理有各种不同形式的表述,有的书还细分为第Ⅰ型与第Ⅱ型抽屉原理.其实从平均数的角度可以把抽屉原理解释得很清楚.平均数具有典型代表意义,可以把平均数作为一个数量标志,用之于寻找具有某种数量特征的事物的存在性[1].简言之,抽屉原理的本质就是最大数≥平均数≥最小数.
从平均数的角度可以巧妙地解决以下两个题目.
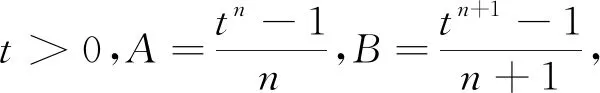

当t>1时,tn,tn-1,…,t,1中tn最大,增加一个最大数后平均数变大,即

当t=1时,显然A=B.
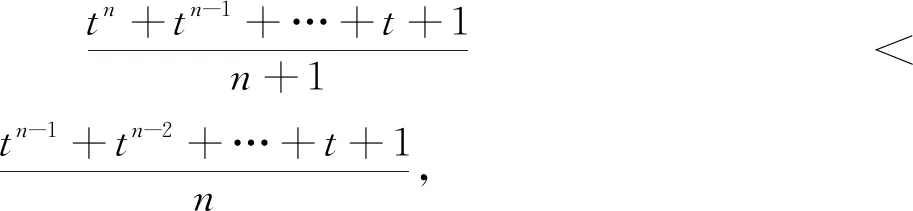
综上,当t>0时,恒有A≤B,当且仅当t=1时等号成立.


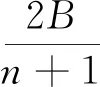
当t=1时,显然A=B.
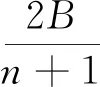
这两题都是从平均数的角度对题目进行了重新解读,充分利用了“最大数≥平均数≥最小数”这一想法,大大简化了数学运算,使题目的结论有很强的直观性.
3 抓住本质,归纳抽屉原理的核心表现形式
在不同的问题情境中,使用抽屉原理进行存在性证明的一个难点,就是如何构造“抽屉”.即如何将研究对象的全体划分为若干个子集,使得这些子集的并集是全集,并且两两交集为空集[2].而在利用抽屉原理解题时,我们更多地将关注点聚焦于构造抽屉的方法[3].例如,通过分割几何图形“构造抽屉”、以讨论对象的特殊性“构造抽屉”“分组构造抽屉”等.也可以从思维策略上将其分为:(1)“直接构造抽屉”,如“生日问题”中的“抽屉”就是直接构造的;(2)“剩余类”构造“抽屉”,如把所有整数按照除以某个正整数m的余数分为m类,叫作m的剩余类[4].
如果我们将目光只局限在构造的方法上,那就会被眼前的问题一叶障目,忽略了抽屉原理的本质.其实在离散的情形中,我们可以将抽屉原理的表现形式分为下列两种.
第二种:若干个球任意放入n个抽屉.结论:要保证有一个抽屉的球数≥m+1,则总球数≥mn+1;要保证有一个抽屉的球数≤m,则总球 数≤(m+1)n-1.
4 运用抽屉原理,巧解经典题
下面笔者给出几道用抽屉原理解决的经典题目.
例2(1988年IMO预选题)一张试卷共有4道选择题,每道选择题有3个选项A,B,C.一群学生参加考试,阅卷后发现:任意3人都有一道题的选项各不相同.试问参加考试的学生最多有多少人?


题号学生编号①②③④⑤⑥⑦⑧⑨1AAABBBCCC2ABCABCABC3ABCBCACAB4ABCCABBCA
综上,所求的答案为9.

例3(1987年国家队选拔赛)给定空间2n个点(n≥2),任意4个点不共面.求证:连接这些点的任意n2+1条边,必存在两个有公共边的三角形.
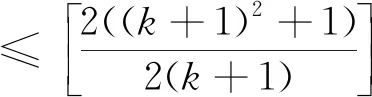
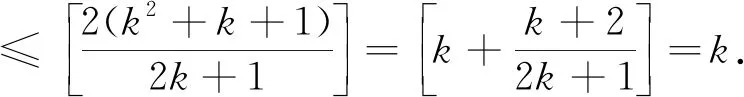
同上,可得新的子图:有2k个顶点,有k2+1条边,由归纳假设,子图中有两个有公共边的三角形.从而原图中有两个有公共边的三角形.
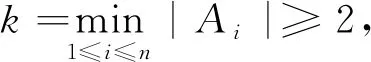
解不妨设|A1|=k,由抽屉原理,只需证A1,A2,…,An中含A1中元素个数总和≥n,等价于平均≥1.
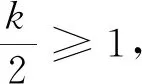
首先,例3运用抽屉原理使归纳证明显得非常的自然,例4将问题转化为证明总体平均大于等于1,再转化为每个局部平均大于等于1,解题过程中不再过多强调抽屉的构造,而是将问题进行有效转化,解法比标准答案简洁很多.


此题有较强的几何背景.一个人在周长为1的圆周上绕圈行走,步长为θ,起点为A,足迹依次为A1,A2,….∀ε>0,∃q∈Z+,使得Aq与A的距离小于ε.上面的证明是典型的应用抽屉原理后其代数化的证明.
抽屉原理的竞赛题变化繁多,命题的形式也异常丰富,被很多“外衣”包装后,学生很容易被困其中.只有理解了抽屉原理的本质,跳出构造抽屉的形式化束缚,才能以不变应万变,让抽屉原理难题迎刃而解.
