一个离散型随机变量问题的剖析与启示
2023-10-18程守山刘天程
曹 辉 程守山 刘天程
(江苏省常州市北郊高级中学 213031) (江苏省常州市正行中学 213000)
《普通高中数学课程标准(2017年版)》将“数学建模”列为六大核心素养之一,在必修课程、选择性必修课程和选修课程中均对数学建模活动作出了具体要求,在核心素养的水平划分中列出了数学建模素养三个水平层级的详细指标[1].随机变量是连接随机现象和实数空间的一座桥梁,它使我们可以借助有关的数学工具来研究随机现象的本质,通过建立不同的概率模型解决有关随机现象的问题.
教科书通过数学建模和数学探究活动或专题(如“建立函数模型解决实际问题”“建立数据模型进行数字特征分析和统计”等),为学生形成积极主动和多样的学习方式提供了有利的条件,有助于激发学生的数学学习兴趣,养成独立思考和积极探索的习惯.
1 问题及背景
2023年苏锡常镇一模第20题:
某小区有居民2 000人,想通过验血的方法筛查出乙肝病毒携带者,为此需对小区全体居民进行血液化验,假设携带病毒的居民占a%,若逐个化验需化验2 000次.为减轻化验工作量,随机按n个人的血液混合在一起化验,若混合血样呈阴性,则这n个人的血样全部阴性;若混合血样呈阳性,说明其中至少有一人的血样呈阳性,就需对每个人再分别单独化验一次.假设每位居民的化验结果呈阴性还是阳性相互独立.
(1)若a=0.2,n=20,试估算该小区化验的总次数;
(2)若a=0.9,每人单独化验一次花费10元,n个人混合化验一次花费n+9元,求n为何值时,每位居民化验费用的数学期望最小.(注:当p<0.01时,(1-p)n≈1-np)
本题的重点是如何选择随机变量来刻画检测方法的优劣,难点是学生在确定随机变量的选择后,如何建立概率模型解决问题.因此,在教学中应可通过“数学探究”“数学建模”等学习活动,让学生参与到这个探究过程中来,感悟数学和现实之间的关联,提高分析和解决实际问题的能力.
上述问题源于苏教版选择性必修第二册第8章“8.2.2 离散型随机变量的数字特征”中的例2[2]:
在一个人数很多的地区普查某种疾病,由以往经验知道,该地区居民得此病的概率为0.1%.现有1 000人去验血,给出下面两种化验方法.
方法1:对1 000人逐一进行化验.
方法2:将1 000人分为100组,每组10人.对于每个组,先将10人的血各取出部分,并混合在一起进行一次化验,如果结果呈阴性,那么可以断定这10人均无此疾病;如果结果呈阳性,那么再逐一化验.
试问:哪种方法较好?
可以看出,苏锡常镇一模第20题与教科书 例2大同小异.例2在待定标准时,难度要大一些.选择怎样的随机变量来刻画检测方法的优劣是解决问题的关键.因此,学生在学习的过程中应加深对教材题目的理解和领悟,同时也要求我们加强对教材例题和课后习题的研究,在教学中渗透建模思想,提高学生的建模能力.
2 多视角探究
由于例2的开放性,学生在探究的过程中给出了自己的观点:
生1:方法1好,理由是如果该疾病有传染性,那么方法2有扩散的风险.
生2:方法1好,理由是从患者个体来讲,采用方法1每人只需抽血1次,而采用方法2每人至少抽血1次.
生3:方法2好,理由是从医院化验的次数来讲,方法2应该优于方法1,具体理由不清楚.
著名数学家怀特海曾说:“数学是对模式的探究”.教材是从分组后每组化验的次数来建立最佳模型,运用数学方法进行探索,使问题得到解决.数学模型的建立有多种方法,怎样选择一个最佳模型,这是一个难点,也是尝试和探索的过程.学生的探究过程,也是关键能力培养的过程.为了使问题指向更加明确,我们从化验次数的角度来刻画检测方法的优劣,下面从三个视角尝试建立模型.
视角1对于方法2,课本上采用分组后每组的化验次数X作为随机变量,X的可能取值为1和11,而且这些人的化验结果是相互独立的,所以分组后每组的化验次数X的概率分布如下:

X111P(1-0.001)101-(1-0.001)10
因为每组化验次数X的均值为E(X)=1×(1-0.001)10+11×[1-(1-0.001)10],所以100组的化验次数的均值为100×{1×(1-0.001)10+11×[1-(1-0.001)10]}≈110.方法1的化验次数为1 000,因此方法2远好于方法1.


Y1101110P(1-0.001)101-(1-0.001)10

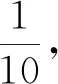

误区1 简单认为随机变量Z的取值是100和1 100.从100组阴性和阳性的角度进行分类,即根据100组阴性,99组阴性1组阳性,98组阴性2组阳性,…,100组阳性,来确定随机变量Z的取值.也可以归纳为100+10k,k=0,1,…,100,其中k代表k组阳性.
误区2 将每人感染的概率和每组感染的概率混为一谈,造成了部分学生认为1组感染的概率是0.001.
3 反思与启示
教材是专家和学者潜心研究并结合多数学生认知水平编写出来的,是集体智慧的结晶.不过,它不可能将编者的思考过程完全用文字反映出来,这就需要教师不断引领学生发现、挖掘、提炼,力争获得其背后所蕴含的知识外延,这恰是命题教师编拟题目的源泉.
无论是哪一阶段的建模环节,学生都需要具备较强的抽象能力作为支撑.但建模能力的培养并不能一蹴而就,需要学生在教师的精心指导和帮助下拾级而上.在教学过程中,教师应有意识地精选典例,引导学生积极开展讨论和探索,强化建模思维训练,达成师生、生生相互学习、共同成长的目标.学生在参与数学建模和探究的过程中,不断地扩充个人认知,提升数学建模和探究能力.
