基于多缩放基调频变换的时频脊线精细化表征方法

丁嘉凯, 王 义, 穆志国, 张光耀, 李 城

(1.重庆大学 机械与运载工程学院,重庆 400030; 2.重庆大学机械传动国家重点实验室,重庆 400030;3.中航西安飞机工业集团股份有限公司,西安 710089)

旋转机械被广泛应用在航空发动机、风力发电机和直升机等传动系统。由于在实际运行过程中,其工况经常发生变化,常常处于变载荷、变转速的工况下,工作环境及其恶劣,极容易发生故障[1-5]。目前,越来越多的旋转机械处在变转速工况下进行工作,如汽车的升降速、飞机的起落过程和航空发动机运行过程等等。当旋转机械处在变转速工况下,所测得的振动信号将失去周期性变化的规律,并呈现出非平稳性出现调频、调幅与调相等现象[6]。传统的频谱分析方法仅能适用于平稳信号的分析,所以针对变转速下的旋转机械故障诊断基于恒定转速的分析方法无法达到目的。因此,如何从非平稳振动信号中提取旋转机械是进行故障诊断的一个重要问题[7-9]。

近年来,国内外许多学者对非平稳振动信号特征提取方法进行了广泛的研究,其主要方法分别为阶次跟踪方法与时频分析方法[10-13]。其中阶次跟踪方法主要是对原始信号进行等角度重采样,转化为平稳信号后再进行频谱分析得到信号阶次谱。但是传统阶次分析中转速需要通过转速计测取,由于测取转速受到安装成本以及安装空间限制,故许多学者在原始信号中进行转速提取,构成无键相阶次分析方法[14-16]。虽然无键相阶次分析可以将时域非平稳信号转化为角域平稳信号,恢复原始信号的周期性,但是等角度重采样过程较为复杂,计算效率较低[17],并且从阶次分析结果可得其存在包络畸变现象,故阶次分析存在一定的误差[18]。

时频分析方法对于提取非平稳信号的时变特性有很大的优势,它是一种能在时频域中定量又能较为直观地描述信号故障特征的分析方法,所以针对变工况下非平稳振动信号时频分析是一种有效的分析手段[19]。但是传统时频分析方法各有优缺点,如短时傅里叶变换(short-time Fourier transform, STFT)和小波变换(wavelet transform, WT)本质上是一种以时频平面上的静态分辨率为特征的线性变换,它被细分为一个恒定面积的基本单元,虽然不存在交叉项干扰的问题,但是其时频分辨率受到Heisenberg不确定性原理的限制,不能在时频分辨率上同时达到最佳[20]。Wigner-Ville分布(Wigner-Ville distribution, WVD)虽然在时频分辨率上较STFT和WT高,但是WVD存在固有的交叉项干扰问题,不适用于分析复杂多分量非平稳信号[21]。以WVD为基础扩展的双线性时频分布如Cohen类分布和仿射类分布,它通过各类核函数进行平滑处理,虽然抑制了交叉项干扰,但是其会造成原始信号发生畸变,从而造成时频分辨率降低[22]。Hilbert-Huang变换对信号的时变具有自适应性,并且具有良好的局部时频聚集能力,但是针对信号中的奇异点较为敏感,容易产生模态混淆等影响,造成产生虚假的本征模态函数(intrinsic mode function, IMF),最终影响分析结果[23]。为了处理以上问题,调频变换(chirplet transform, CT)应运而生,它是针对用于分析线性瞬时频率(instantaneous frequency, IF)恒定的调频信号[24]。但是,当待分析信号具有非线性IF轨迹时,CT也不能保证时频表征的精度。为了解决这个问题,Peng等[25]提出了一种多项式chirplet变换(polynomial chirplet transform, PCT)时频分析方法,它通过使用多项式函数代替线性调频核,可以逼近非线性IF轨迹,最终得到时频能量集中较好的时频表征。虽然PCT在分析强非线性IF信号时表现出了较强的时频分辨率,但是在变工况下,实际振动信号的复杂性和多样性导致我们不能使用一个单独的多项式模型来描述所有的信号分量。此外,由于PCT需要在传统的时频表征方法上进行IF估计,因此需要初始化的时频表征具有一定的能量集中度,否则无法达到精细化时频表征[26]。国内外针对IF脊线精细化表征做了许多研究[27],但是在强噪声和多分量的情况下,由于噪声和无关分量的影响对于弱分量提取较为困难。

本文针对CT在分析非平稳振动信号时其核函数固定不变导致IF轨迹无法达到精细化表征的问题,本文提出了一种MSBCT精细化时频表征方法,理论分析结果表明该方法可利用高阶相位算子将核函数精确逼近IF轨迹,使得该方法在变转速工况下针对非线性IF轨迹可得到精细化时频表征。并通过仿真和试验验证该方法可适用于处理强噪声、多分量的信号,并且可应用于变转速旋转机械故障诊断,能够直观地提取故障特征频率。

1 多缩放基调频变换

1.1 CT理论

信号x(t)∈L2(R)的chirplet变换基础理论公式可表示为

(1)

式中:s(t)为信号x(t)经Hilbert变换得到的解析信号,s(t)=x(t)+jH(x(t));φ(t)为相位函数;h(t)为一个归一化的时不变高斯窗函数并且h(t)∈L2(R)。采用的高斯窗函数可表示为

(2)

式中,σ代表高斯窗函数的标准差。

根据Ville[28]提出的理论可知,信号的瞬时频率可以由解析信号的相位导数来计算得到,则解析信号s(t)可以表示为

(3)

(4)

式中:t0∈R为选择的时间中心;φ(t0)∈R为t0时刻的信号频率大小,令C=φ′(t0),在CT中C∈R为调频率。CT核心为通过旋转频率来匹配信号中的瞬时频率(IF)轨迹,从而获得具有较高能量浓度的时频分布(time-frequency representation, TFR)。将式(4)进行二次求导可得调频率C的具体表达式如下所示

φ(t0)+C(t-t0)

(5)

(6)

式中:α∈[-π/2,π/2]为旋转角度;C为一个常数。

当旋转角度的正切值tanα等于信号的IF轨迹的斜率dφ(t)/dt时,对应的TFR的能量浓度最高。CT调频率与信号的IF轨迹斜率匹配原理如图1所示。图1时频图中包含信号分量φ1(t)。φ1(t)IF轨迹斜率为-tanα,CT采用的是一个时不变高斯窗进行时频变换,其中窗函数的窗长固定不变为WL。当C为0时,此时的CT即为STFT,如图1中虚线所示,此时的CT窗函数与信号分量存在一个夹角α,得到的TFR会存在一定的能量泄露造成频谱模糊效应,得不到具有较高能量浓度的TFR。当CT中的C为-tanα时,此时C等于信号IF轨迹的斜率,造成的能量泄露较少可得到信号较高能量浓度的TFR,如图1中实线部分。

图1 传统CT调频率与信号的IF轨迹斜率匹配原理Fig.1 Matching principle of traditional CT kernel function and signal IF trajectory

1.2 CT方法的局限性

由于CT变换的调频率C是固定值,所以它在处理具有相同IF轨迹斜率的多分量信号具有优势,它能得到具有较高的能量浓度的TFR。但是实际信号中通常不会存在一致的IF轨迹斜率多分量信号,比如机械装备中轴承在变转速的条件下运行时,出现故障后会产生不同的故障频率,这些故障IF轨迹斜率通常不一致。所以,CT在处理不同IF轨迹斜率多分量信号也会产生能量泄露导致频谱模糊效应。

因此,在具有不同IF轨迹斜率的多分量信号中进行CT变换时,要在同一时刻不同频率分量上达到最佳的能量浓度是不可能实现的,这是由于CT的理论基础决定的。故需要对传统CT变换进行改进,需要针对具有不同IF轨迹斜率的多分量信号进行C的自适应选取,以至于得到最佳能量浓度的TFR,为后续的变工况下机械装备故障诊断与非平稳信号时频脊线精确提取奠定基础。

1.3 MSBCT方法

针对不同IF轨迹斜率的多分量信号,其IF函数利用泰勒公式进行展开,文献[26]与文献[29]均将其展开至低阶形式,本文利用泰勒公式将IF函数展开至高阶形式,可针对多个信号分量IF轨迹斜率进行匹配,并根据实际信号在分析频率范围内存在多个分量信号的特性,得到MSBCT方法中高阶相位算子具体形式如下所示

φ(t0)+φ′(t0)(t-t0)+

(7)

联合式(3)和式(7)可得MSBCT方法的具体表达式为

exp(-j2πφ(t))dt

(8)

由于信号的IF不能提前知道,但是IF轨迹斜率的角度可以知道其范围,其角度范围从-π/2变化到π/2。则多信号IF轨迹斜率角度可设置为

(9)

(10)

(11)

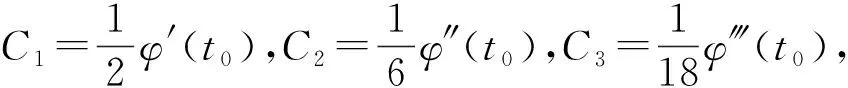
C1=Atanα

(12)

C2=Btanαtanβ

(13)

C3=Ctanαtanβtanθ

(14)

式中,A,B,C分别为等式系数,即存在系数A,B,C使得式(12)～(14)成立。

将式(12)～(14)代入式(8)中,可得:

Atanα(t-t0)2+…+Btanαtanβ(t-t0)3+…+

Ctanαtanβtanθ(t-t0)4))·…·h(t-t0)·

exp(-j2πφ(t))dt

(15)

由于解析信号扩展为多项式形式,则MSBCT方法中的核函数需进行泰勒展开并且与解析信号中多项式抵消项,则可得到TFR的最佳峰度,其最佳峰度表达式为

(16)

式中,V为TFR的最大范围。

此时得到的即为最佳浓度的TFR,所以最终MSBCT表达式为

exp(-j2π(t+Atanα(t-t0)2+…+

Btanαtanβ(t-t0)3+…+

Ctanαtanβtanθ(t-t0)4))dt

(17)

本文确定MSBCT参数的有效方法为通过生成一系列IF轨迹斜率夹角α,β和θ的组合来生成TFR。对于每个时间点找出TFR能量浓度最高的参数组合作为最佳参数组合。其中通过式(16)来寻找TFR最优能量浓度,然后依次迭代确定每个时间点的最优参数组合,从而得到整段信号的最优MSBCT参数组合。其中,MSBCT最优参数组合表达式为

(18)

2 性能评估

该部分本文利用仿真信号对MSBCT算法进行性能评估,验证其是否具有在时变工况下对时频脊线精细化表征的能力,并且利用最新的时频变换方法与MSBCT算法进行性能比较,如VSLCT,SBCT,CWT和STFT。

本文利用一个IF轨迹斜率时变的多分量信号进行MSBCT时频表征,从而验证MSBCT算法可针对时变工况下IF轨迹进行精确化时频表征。本章采用的仿真信号s1(t)如下所示

(19)

式中,φ1(u)为基频。其表达式如下

(20)

在此案例中仿真信号s1(t)的采样频率为100 Hz,采样时间为50 s。并且其他倍频与基频之间的关系如下

(21)

仿真信号s1(t)的时域图和频域图如图2所示。s1(t)为调频调幅信号,所以利用MSBCT算法对仿真信号s1(t)进行精确时频表征,其TFR如图3所示。MSBCT算法可将仿真信号s1(t)进行精确时频表征,在A部分IF轨迹紧邻分量,MSBCT将4条紧邻分量进行精确的时频表征,没有产生任何时频模糊现象。在B部分IF轨迹斜率突变处也得到了清晰的时频表征图。所以图3的结果可以看出,MSBCT可在时变工况下将时频脊线进行精细化表征。

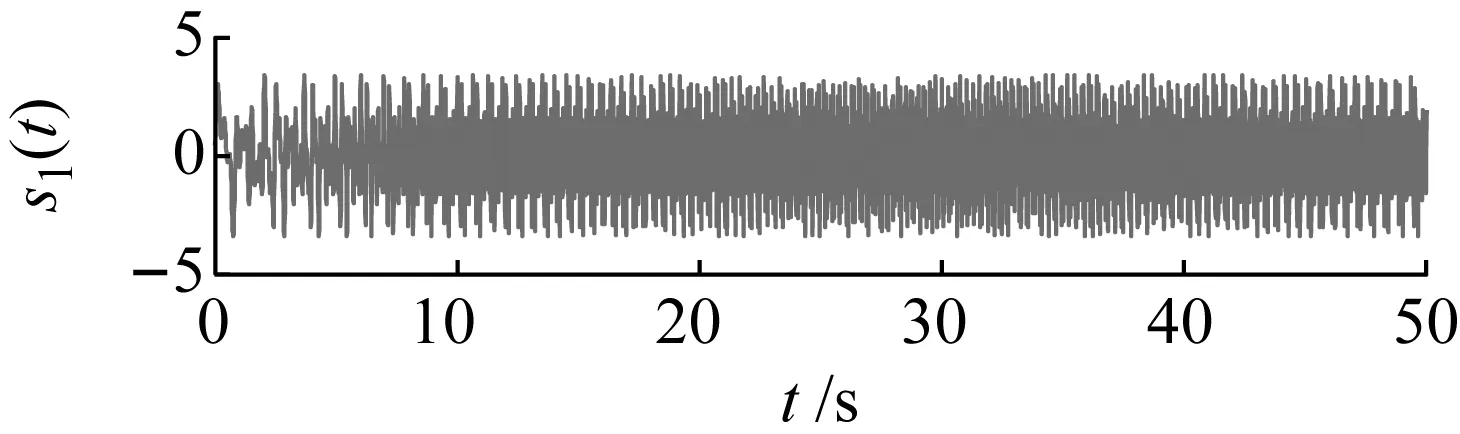
(a)

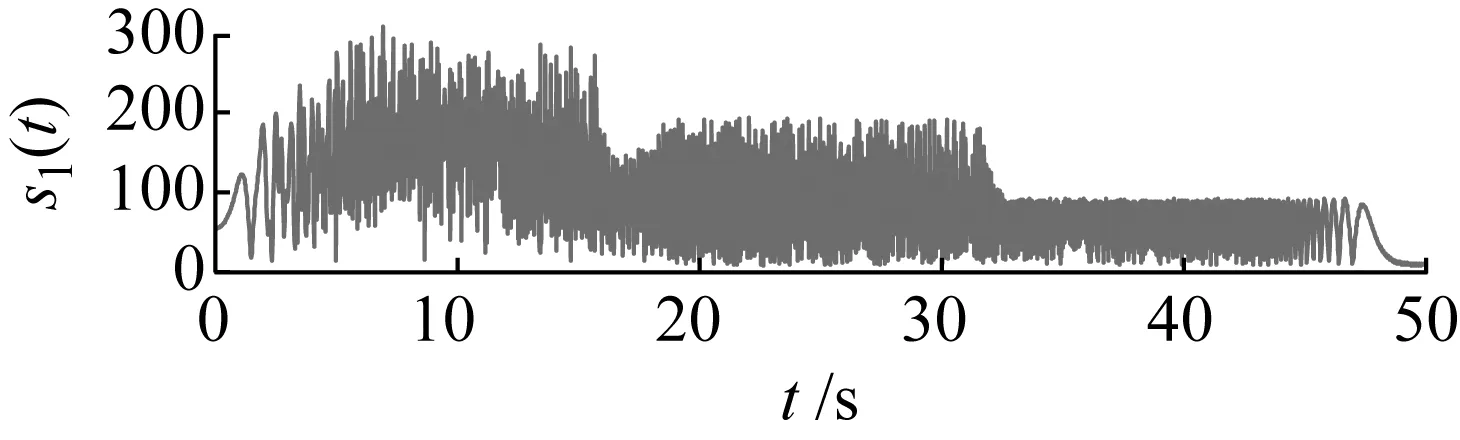
(b)图2 仿真信号s1(t)的时域图和频域图Fig.2 Time-domain and frequency-domain diagrams of the simulation signal s1(t)

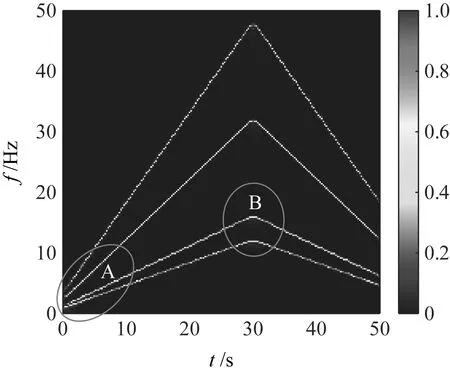
图3 利用MSBCT算法对仿真信号s1(t)的TFRFig.3 The TFR of s1(t) by using MSBCT algorithm

利用不同的时频变换方法对仿真信号s1(t)进行时频表征,其TFR如图4所示。其中,SBCT与STFT的窗口长度设置为128。如图4(a)所示,从整体看来,VSLCT算法得到的TFR均存在时频模糊问题,尤其是在A和B两个部分,其中在A处发生了频谱模糊效应。在B处发生了频散现象,使得此处的能量发生了泄露。如图4(b)所示,SBCT在A部分IF轨迹相隔较近处发生了时频模糊现象,在其余部分获得了较好的TFR,但是其时频能量集中度较差,其整体效果不如MSBCT算法。如图4(c)所示,从整体可得CWT算法得到的时频能量集中较VSLCT和MSBCT效果较差,并且在A部分发生了频谱模糊现象,这导致了CWT无法对IF轨迹紧邻分量信号进行准确的时频表征。如图4(d)所示,STFT所得到的时频图和CWT的类似,并且STFT所得到的时频能量集中较CWT更差,其中第一条和第二条IF轨迹在整个时间段均发生了频谱模糊现象,故STFT也无法对IF轨迹紧邻分量信号进行精确的时频表征。表1为利用MSBCT和不同时频变换方法对仿真信号s1(t)分析所得到的运行时间。由表1可知,本文所提MSBCT算法相比于CWT和STFT传统时频变换方法所用时间较长,但是CWT和STFT所得到的时频表征效果不佳,无法得到精细化时频表征,并且时频能力不集中。但是,MSBCT所运行时间相比于SBCT和VSLCT等精细化时频表征方法较短,可突出MSBCT算法在精细化时频表征方法中的优越性。

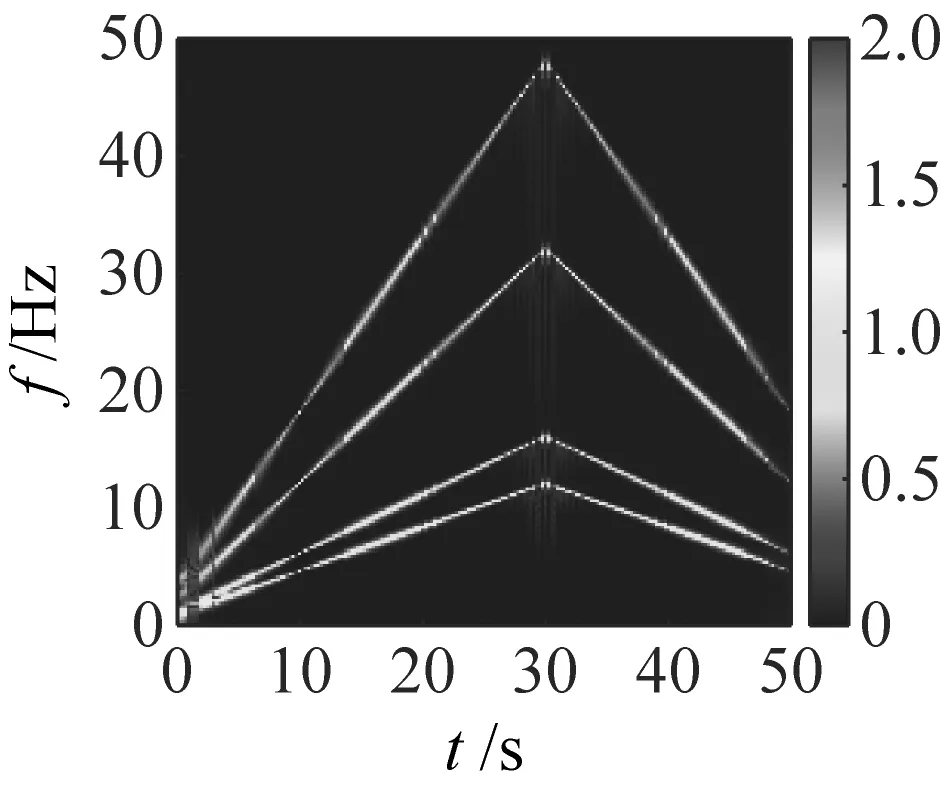
(a) VSLCT

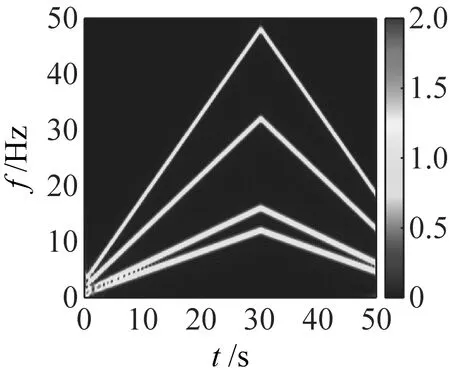
(b) SBCT

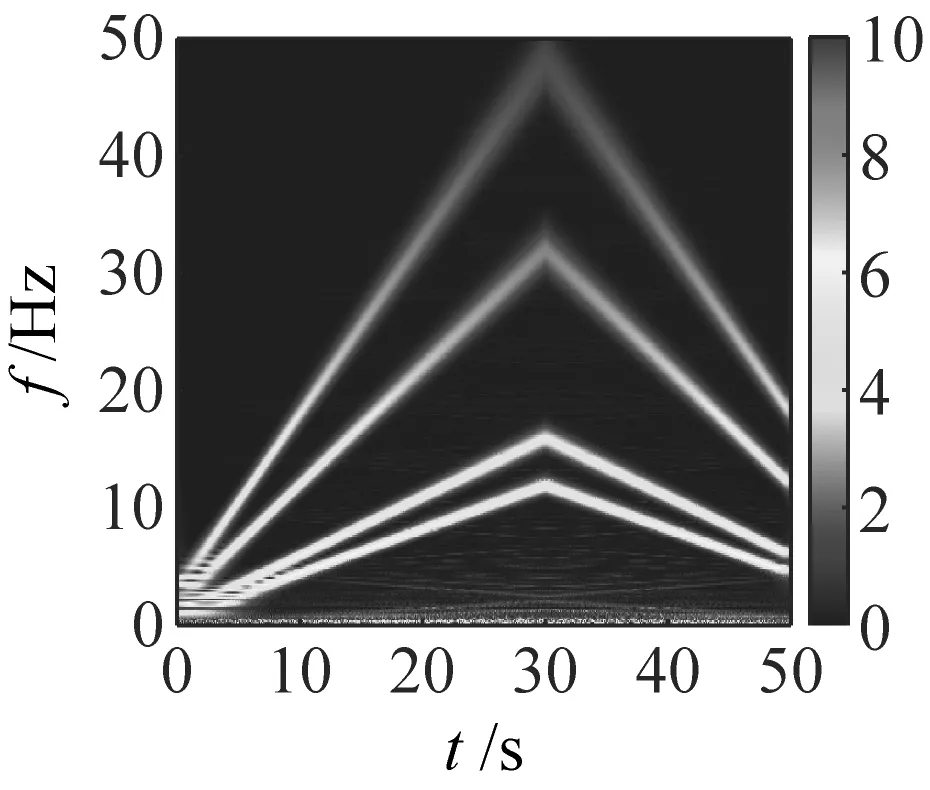
(c) CWT

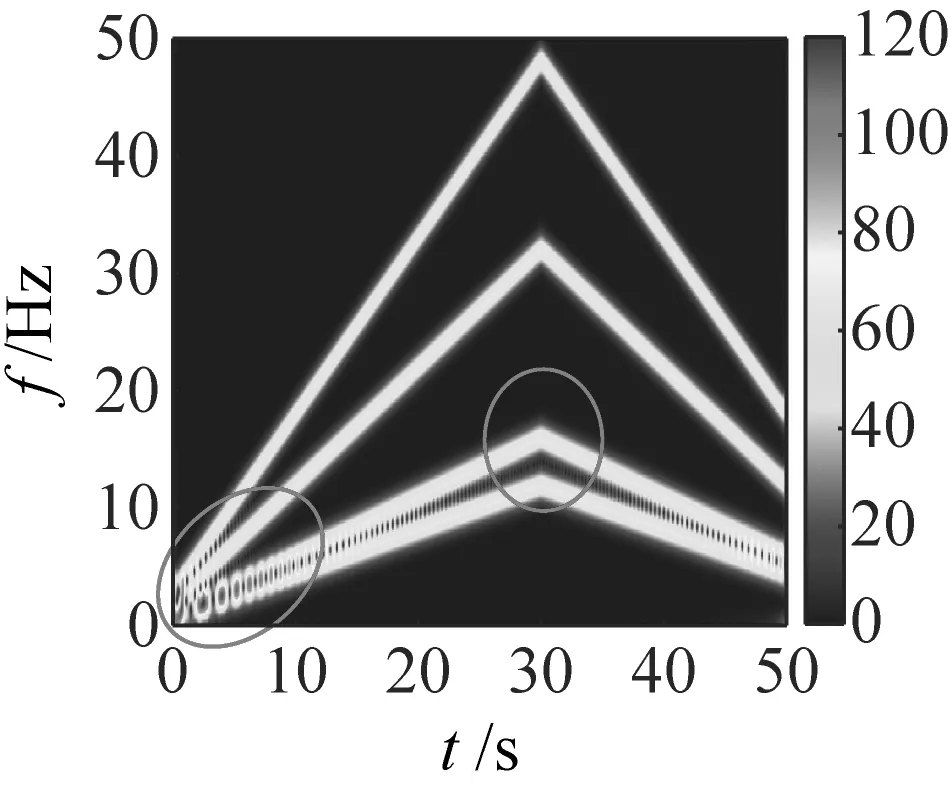
(d) STFT图4 仿真信号s1(t)的TFRFig.4 TFR of simulation signal s1(t)

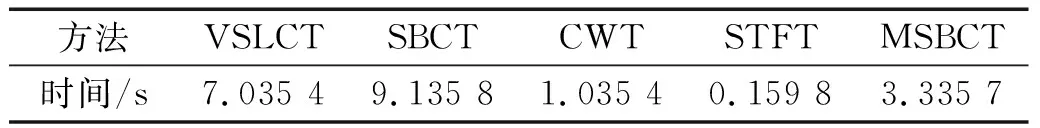
表1 不同时频变换方法分析仿真信号s1(t)所用时间Tab.1 The running time of simulation signal s1(t) obtained by different time-frequency transform method

为了进一步得到MSBCT算法对噪声抑制的效果,本文在式(19)的基础上加入SNR=-5 dB的高斯白噪声进行时频表征,其公式如下所示

(22)

式中,n(t)为信噪比为-5 dB的高斯白噪声。

对于加入SNR=-5 dB的高斯白噪声仿真信号s1(t),本文利用MSBCT和VSLCT对其进行时频表征,所得到的时频图如图5所示。如图5(a)所示,对于加入-5 dB噪声再利用MSBCT对其进行时频表征后,从整体所看四条IF轨迹得到了精确表征,并且时频能量集中较好,并且在A和B两个部分的IF轨迹时频表征均较为准确,充分说明MSBCT对噪声抑制有着较强的优势。如图5(b)所示,VSLCT算法在A和B两个部分均发生了时频模糊现象,并在整个时频面上对于噪声抑制没有MSBCT算法效果好。

(a) MSBCT

3 试验验证

在本章内容中MSBCT算法被应用至变转速轴承内圈故障信号精细化时频表征,本文采用渥太华大学SpectraQuest机械故障模拟器去生成变转速轴承内圈故障信号[30],其试验台如图6所示。该试验台由电机、编码器、测试轴承、健康轴承、AC和加速度传感器组成。其中测试轴承型号为ER16K,轴承节圆直径为38.52 mm,滚子直径为7.94 mm。加速度传感器安装在测试轴承上方,便于采集变转速轴承故障信号。其中,本试验采样频率为200 kHz,采样时间为10 s。在此案例中,本文选取轴承转速先升后降的工况,具体为轴承转速从14.8 Hz升高至21.7 Hz,然后降至13.6 Hz。由文献[31]提供该轴承内圈故障阶次为5.43,故该轴承内圈一阶故障频率fI具体变化为从80.36 Hz升高至117.83 Hz,然后降至73.85 Hz。本文选取的变转速滚动轴承内圈故障信号时域图和频域图如图7所示。由于滚动轴承的转速是随着时间变化的,导致其发生频谱模糊效应,所以利用MSBCT算法对其进行时频表征,在时频域上对其进行滚动轴承内圈故障IF轨迹进行分析,从而进行故障诊断。

图6 变转速滚动轴承内圈故障试验台Fig.6 Rolling bearing inner ring fault test rig under variable speed

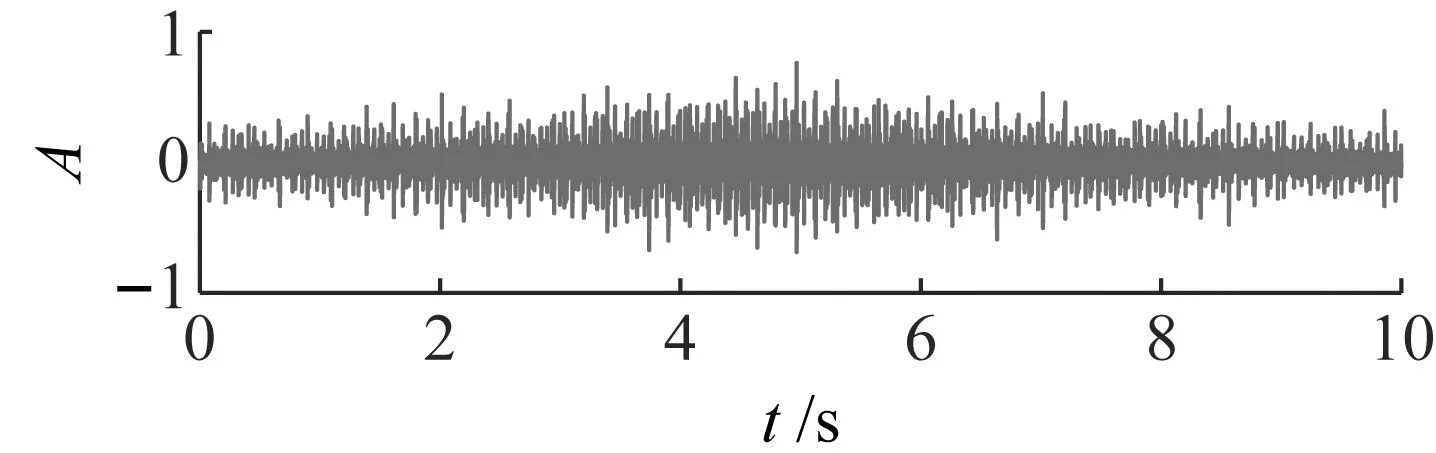
(a)

(b)图7 变转速滚动轴承内圈故障信号的时域图和频域图Fig.7 Time-domain and frequency-domain diagrams of variable speed rolling bearing inner ring fault signal

在进行时频表征之前,本试验进行以下操作,由于采样频率过高,故对原始信号进行带通滤波和降采样操作。首先本文利用‘db10’小波基的5层小波包算法对原始振动信号进行带通滤波操作,选取第一层滤波信号进行降6倍采样操作得到最终分析信号,再利用MSBCT对信号进行时频表征如图8所示。滚动轴承内圈故障fI,2fI,3fI和4fIIF轨迹均被MSBCT算法精确表征,并且在整个时频面上MSBCT算法对噪声有一定程度上的抑制作用,对于该方法得到的2fI来说,MSBCT有着较好的时频能量集中。对于图8中的A和B两部分,该处的IF轨迹斜率发生了突变,MSBCT算法也可将其精确表征。再利用不同的时频变换算法与MSBCT进行效果对比,其时频图如图9所示。

图8 利用MSBCT算法对变转速滚动轴承内圈故障信号的TFRFig.8 TFR of rolling bearing inner ring fault signal under variable speed by using MSBCT algorithm

(a) VSLCT

(b) SBCT

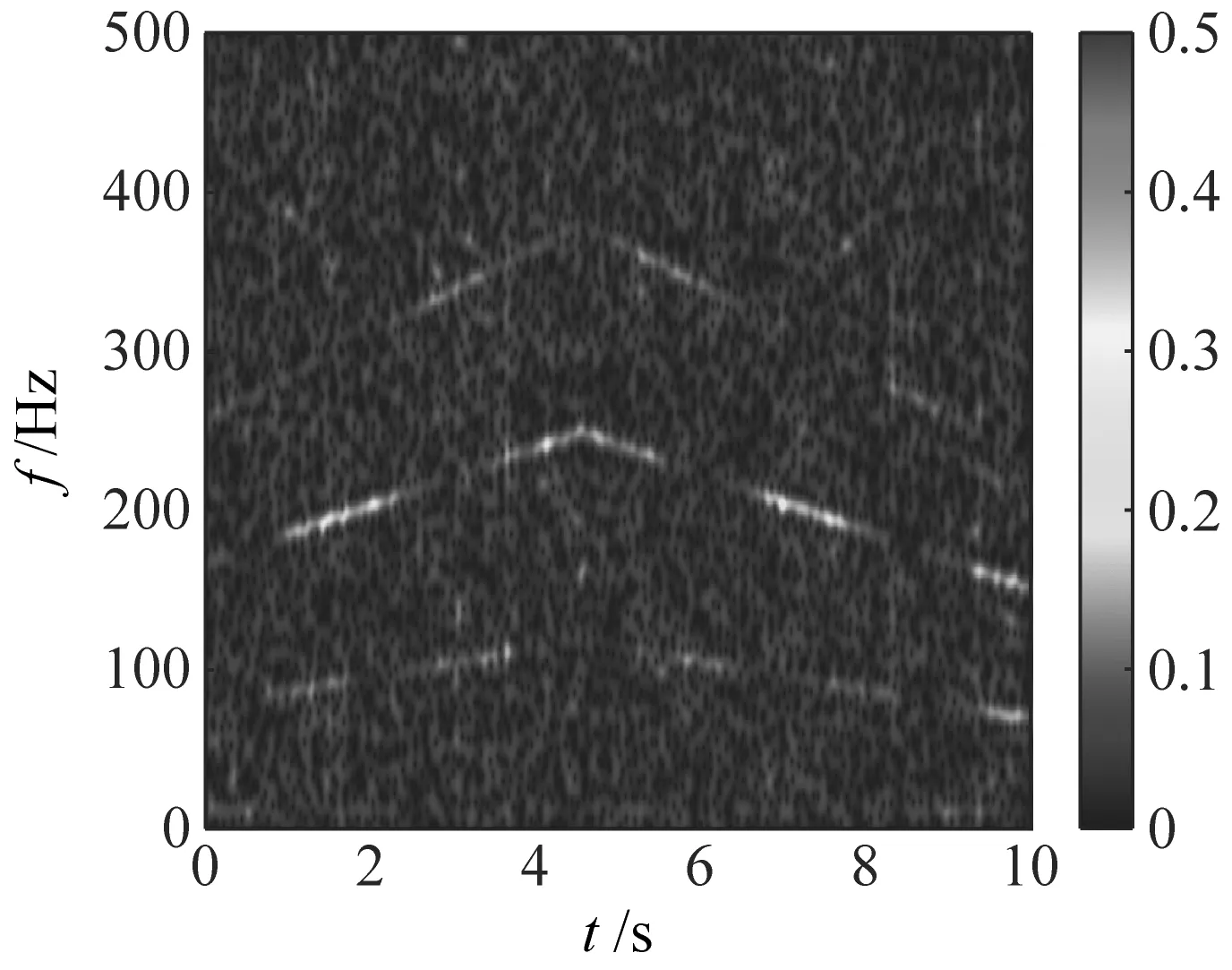
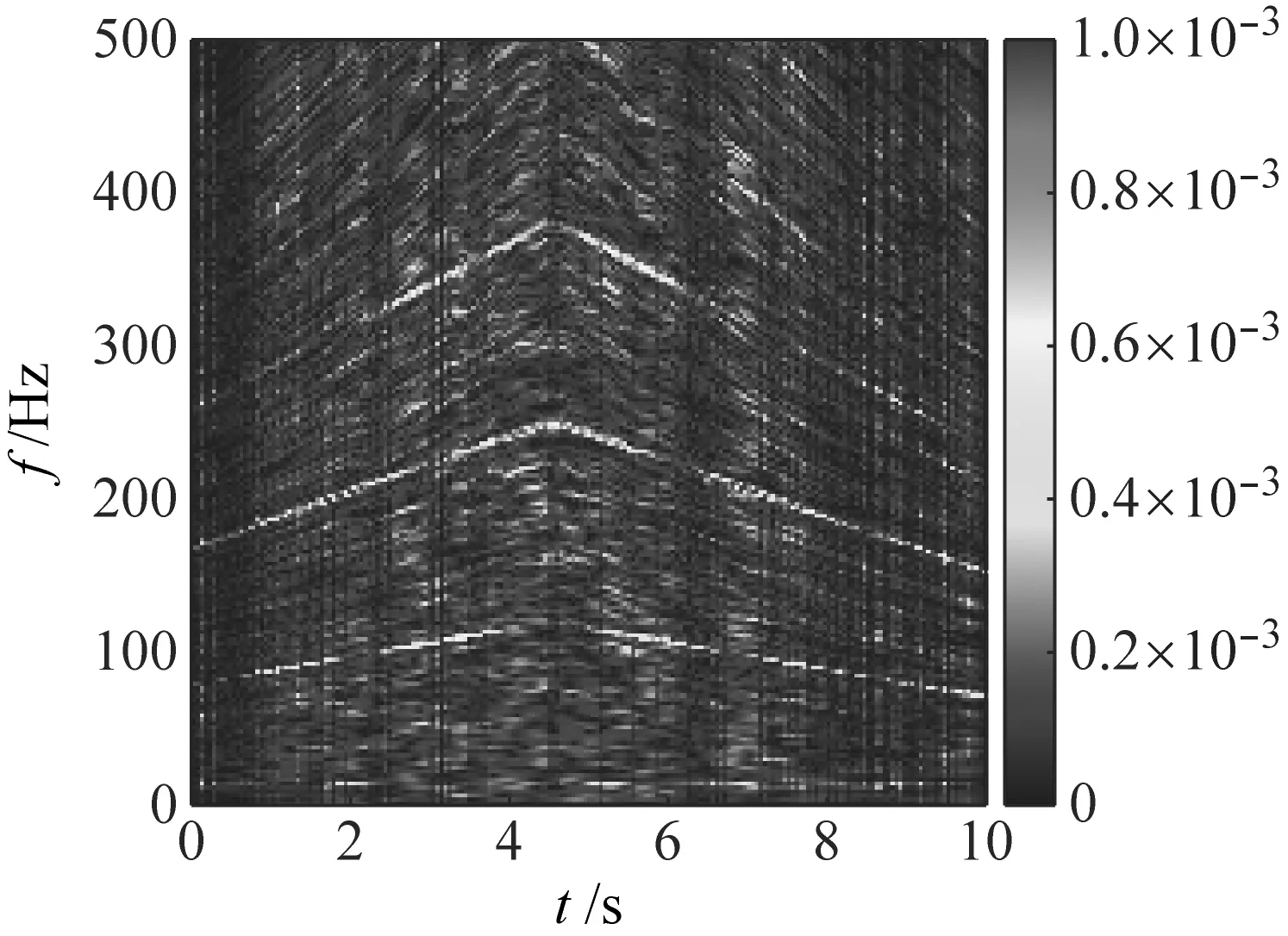
(d) STFT图9 变转速滚动轴承内圈故障信号的TFRFig.9 TFR of rolling bearing inner ring fault signal under variable speed

在本案例中SBCT和STFT的窗长均设置为128。如图9(a)所示,滚动轴承内圈故障fI,2fI和3fI可以从时频图中得到,但是4fI较为模糊无法准确得到。从整体看来,VSLCT算法得到的TFR均存在时频模糊现象,尤其是在初始时间端和结尾时间段均发生了较为严重的时频模糊现象。其中在A和B处时频表征发生了时频模糊问题,造成了频谱模糊效应。如图9(b)所示,SBCT算法可将滚动轴承内圈故障fI,2fI和3fI从时频图中大致得到,但是4fI较为模糊无法准确得到。并且SBCT得到的TFR中IF轨迹时频能量浓度较差,时频面模糊问题较为严重,噪声抑制效果较差。如图9(c)所示,滚动轴承内圈故障fI和2fI可以从时频图中大致得到,但是其IF轨迹也发生了模糊,3fI和4fI较为模糊无法准确得到。从整体可得CWT算法得到的时频能量集中较VSLCT和MSBCT效果较差,整体受噪声影响较为严重。并且在A和B处CWT无法对其进行准确的时频表征。如图9(d)所示,滚动轴承内圈故障fI,2fI和3fI可以从时频图中大致得到,但是4fI较为模糊无法准确得到。并且STFT所得到的时频图较CWT的时频能量较为集中,但是STFT所得到的时频图效果受到噪声影响较为严重,在整个时频面上均发生了时频模糊现象,时频能量集中较MSBCT更差。表2为利用MSBCT和不同时频变换方法对变转速滚动轴承内圈故障信号分析所得到的运行时间。由表2可知,MSBCT所运行时间较VSLCT和SBCT等精细化时频表征方法较短。

表2 不同时频变换方法分析变转速滚动轴承内圈故障信号所用时间Tab.2 The running time of variable speed rolling bearing inner ring fault signal obtained by different time-frequency transform method

综上所述,针对变转速轴承内圈故障信号利用MSBCT算法可对其进行精细化时频表征,并且在IF轨迹斜率突变处的时频能量较为集中,时频表征整体没有发生模糊现象,与其他算法进行对比突出了它在变工况下对时频脊线精细化表征的优势。

4 结 论

本文提出了一种新的时频分析方法,称为MSBCT。它克服了传统CT变换的缺点,主要针对在变工况下对非线性IF轨迹分量有着较高的时频能量集中度,并且在时频域内可一定程度上抑制噪声信号的影响,克制时频模糊现象。在MSBCT算法中,理论分析结果表明该方法可利用高阶相位算子将MSBCT方法核函数精确逼近IF轨迹,使得MSBCT算法可针对变转速工况下的IF轨迹得到精确的时频表征。仿真结果和试验结果均得到非线性IF轨迹的精细化时频表征,并且与最新的时频分析方法进行比较验证了MSBCT算法的优势性。