不同应力加载速率下深埋泥岩力学特性与扩容特征试验研究

李 可 ，余伟健 ，廖 泽，郭涵潇，潘 豹，KHAMPHOUVANH Viengvilay，杨 杰

(1.湖南科技大学 资源环境与安全工程学院,湖南 湘潭 411201；2.贵州理工学院 矿业工程学院,贵州 贵阳 550003；3.湖南科技大学 煤炭资源清洁利用与矿山环境保护湖南省重点实验室,湖南 湘潭 411201)

西南地区是我国南方的重要赋煤区和煤炭资源产地，从下古生界到新生界都有聚煤地层，以晚二叠世龙潭期—长兴期的煤最为重要，占总资源量的85%以上[1]。通过现场调研和钻取岩心观察发现，深部龙潭组地层岩性以泥岩为主，不同层位的泥岩主要成分差异也较大，主要有炭质泥岩、钙质泥岩、铁质泥岩等[2]。陈宗基和康文法[3]认为，地下工程开挖致使围岩部分应力解除即卸荷发生，岩石在偏应力作用下体积产生非线性增长的力学过程即为扩容。根据康红普[4]分析，巷道围岩扩容引起的底臌量约占巷道总底臌量的1/3[4]。因此，需要对深部泥岩的力学行为特性和扩容特征进行研究。

岩石的力学扩容产生与否，既取决于岩石介质物理性质，也取决于应力状态，主要是偏应力的作用[5]。近年来，针对岩石扩容现象，陈宗基和康文法[3]推导了与时间有关及无关的扩容本构方程，并给出了相关扩容参数测试方法。康红普[4]推导了瞬时扩容引起的底臌位移量计算式，并进行了实例计算验证。一些学者[6-13]研究了脆岩、硬岩、弱胶结、盐岩等各种岩石扩容变形本构模型和扩容判据等。YUAN 等[14]提出了剪胀扩容指数的概念，定义为任何特定围压下的表观扩容角与单轴条件下扩容角之比。之后其他学者[15-19]在YUAN 的理论基础提出了适用于不同类型岩石和不同荷载条件的扩容角模型。ZHAO 等[20]建立了考虑围压和塑性剪切应变影响的扩容角模型。荣浩宇等[21]试验后认为三轴压缩条件下，岩石变形表现为轴向压缩以及沿最小主应力方向扩容。TRIVEDI[22]详细分析了平面应变和轴对称情况下的剪胀扩容对强度的影响。也有一些学者[23]研究了单轴压缩试验中扩容弹性/黏塑性本构模型。

荷载加载速率对岩石试样的力学强度参数和变形参数测试结果有很大的影响[24-26]。通常，岩石强度和平均弹性模量随着应力加载速率的增加而增加[27-29]，也有一些学者提出不同的观点，认为对于不同强度等级的岩石，随着应力加载速率的增加，单轴抗压强度的增加并不具有普遍性[30-32]。ALKAN[33]认为扩容起始强度取决于应力加载速率和孔隙压力，随着应力加载速率的增加，扩容起始强度减小。尹小涛等[34]认为随着应变率的提高，岩石的峰值强度提高，变形参数也提高。何松等[35]试验后认为黏土岩峰值强度与加载速率近似线性相关。王云飞等[36]分析了不同加载速率下砂岩试样的强度、应变能、微观损伤和宏观破裂特征的变化规律。

上述研究在理论研究和工程应用中发挥了重要的指导作用。然而，不同位置的泥岩性质有很大差别[37-38]，目前对埋深较大的泥岩，特别是在我国西南地区广泛分布的二叠系龙潭组泥岩的力学特性研究以及其扩容特征的研究较少，笔者对矿山现场钻取的埋深近1 300 m 的岩石试样做了系列试验，包括XRD衍射试验、SEM 岩石断口形貌电镜扫描试验和不同加载速率下的单轴压缩试验等，以期揭示深埋泥岩力学特性与扩容特征。

1 试样来源与试样特征

1.1 试样来源

试样来源于我国西南地区贵州省盘州市某煤矿，矿井生产规模240 万t/a，该矿含煤岩系为二叠系龙潭组，属海陆过渡相沉积地层，含煤26～38 层，其中可采煤层14 层，样品取自该煤矿龙潭组中部的17 号煤层与22 号煤层之间的岩层中，2 层煤的平均间距是37.7 m，取样位置地层倾角为33°，样品的埋深是1 289～1 294 m，取样直径为50 mm，主要岩性为灰褐色薄层钙质泥岩。现场钻取的岩心如图1 所示。本试验采用岩石切割机将图1 中试样切割后，采用TXSHM200C 型程控双端面磨石机将岩样打磨成长度100 mm、直径50 mm 的标准试样。在烘干机中105 ℃下干燥24 h 后，采用型号为RSMSY5 的声波检测仪测试各试样纵波波速，选择波速差5%以内的8 个试样，如图2 所示。本文试样加工标准和力学试验过程均依据ISRM 发布的“测定岩石材料在单轴压缩下变形性质的方法”[39]。

图1 现场钻取的岩石试样Fig.1 Samples obtained from the mine site drilling

图2 实验室加工完成的试样Fig.2 Specimens processed in the laboratory

测量得到加工完成后试样参数见表1。

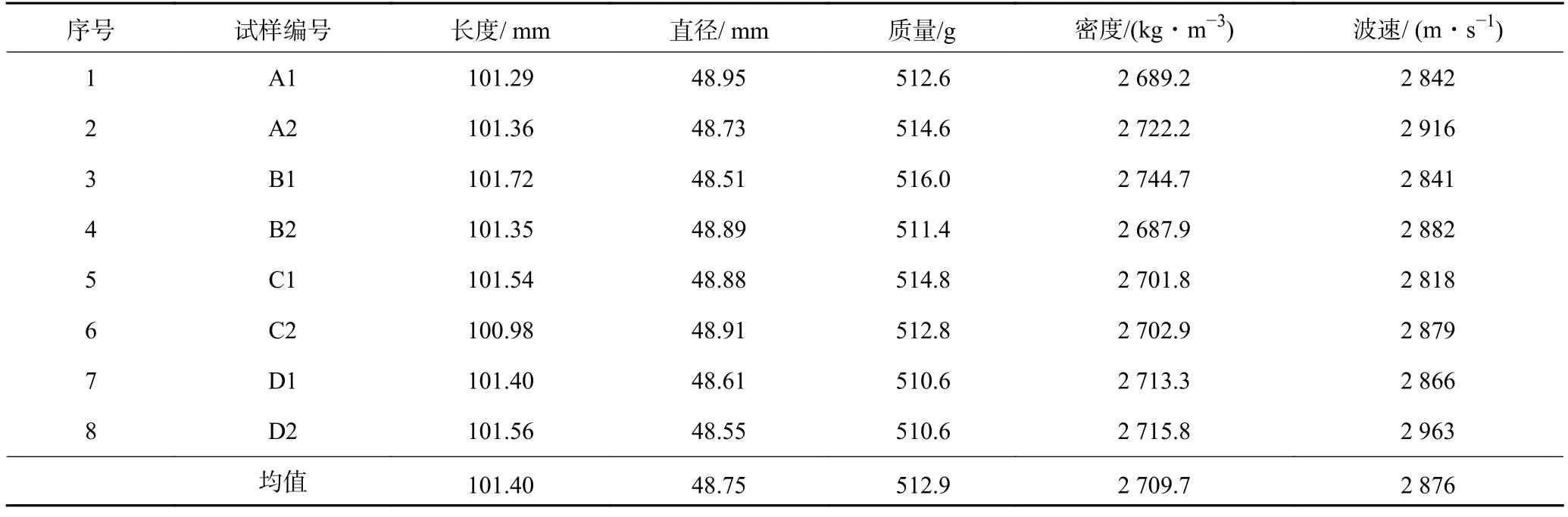
表1 加工制备完成的试样参数Table 1 Specimen parameters after processing

1.2 XRD 衍射试验

为了分析泥岩试样的矿物组成，采用型号为Uitima IV 的X 射线衍射仪对试样进行检查，检查结果如图3 所示。依据“多晶体X 射线衍射方法通则”(JY/T 0587—2020)，采用绝热定量法对试验结果进行处理，可知该泥岩主要含有长石(钠长石质量分数为29.8%、钾长石质量分数为13.3%)、石英质量分数为25.0%、绿泥石质量分数为16.7%、黄铁矿质量分数为9.6%、方解石质量分数为5.6%等6 种矿物，其中以斜长石为主，质量分数达43.1%。

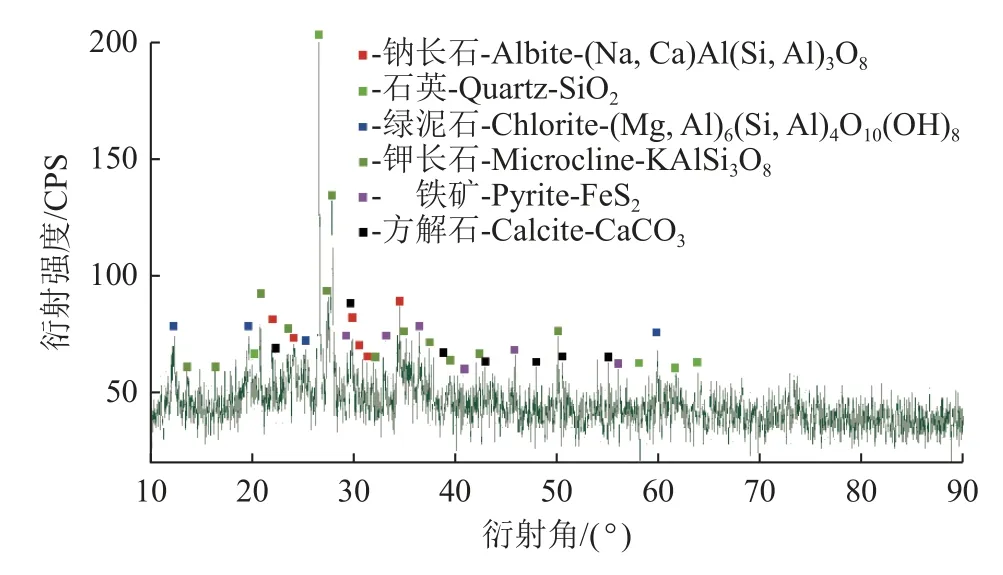
图3 泥岩试样X 射线衍射Fig.3 XRD pattern of mudstone

1.3 岩石断口形貌观察

为了观察岩石细部结构，采用Nova Nano SEM 450 型热场电镜扫描仪对岩石断口进行扫描，得到不同放大倍数的SEM 图片，如图4 所示。从图4 可以看出，泥岩岩石内部各矿物成分的分布是不均匀的，主要成分长石(钠长石和钾长石)呈条带状分布，长石间填充其他矿物，填充物以绿泥石为主，绿泥石中夹杂点状分布的石英，黄铁矿和方解石颗粒状夹杂赋存在绿泥石中。各种矿物的分布表现出强烈的非均质性，该性质也是岩石表现出各向异性的主要原因。

从图4 中的SEM 图片可以看出，岩石表面延伸到内部的微裂隙是非常发育的，采用PCAS 软件读取500 倍和1 000 倍SEM 图片中孔隙数据，结果如图5所示，计算得到其表面孔隙率分别为4.48%和3.63%。孔隙的多少直接影响岩石的力学性能，孔隙越多，岩石的力学强度越低。泥岩岩石孔隙和裂隙的广泛分布以及其非均质性在很大程度上降低了它的强度，这也是现场取样时，难以取得完整岩心的重要原因。

图5 PCAS 读取的岩石表面孔隙数据分布Fig.5 Pore distribution on the rock surface processed by PCAS

2 岩石力学试验方案

本试验加载设备为RMT-150C 型岩石压力试验机，采用DH3816N 型静态应变测试仪和丝绕式电阻片进行变形监测。试验系统如图6 所示。

图6 单轴压缩试验系统Fig.6 Uniaxial compression testing system

实验室加工长度100 mm、直径50 mm 试样8 个，2 个试样一组分为4 组，4 组试样分别采用不同的加载速率线性递增力加载控制，加载速率分别为0.1、0.5、2.0 和5.0 kN/s，即0.05、0.25、1.00 和2.50 MPa/s，加载至试件破坏，加载系统压头自动退回，试验完成后，试样如图7 所示。每个试样粘贴4 个应变片，2 个监测轴向变形，2 个监测径向变形，加载过程中实时监测变形数据。

图7 单轴压缩试验后试样形态Fig.7 Damaged shape of specimens after UCS test

3 泥岩岩石力学特性

3.1 试验结果

本试验在0.1、0.5、2.0 和5.0 kN/s 等4 种不同加载速率下8 个泥岩试样的单轴压缩试验结果见表2。由表2 可知，各组泥岩岩石试样单轴抗压强度均值最小为26.8 MPa，均值最大为36.5 MPa。平均弹性模量值最小为3.5 GPa，最大为5.9 GPa。

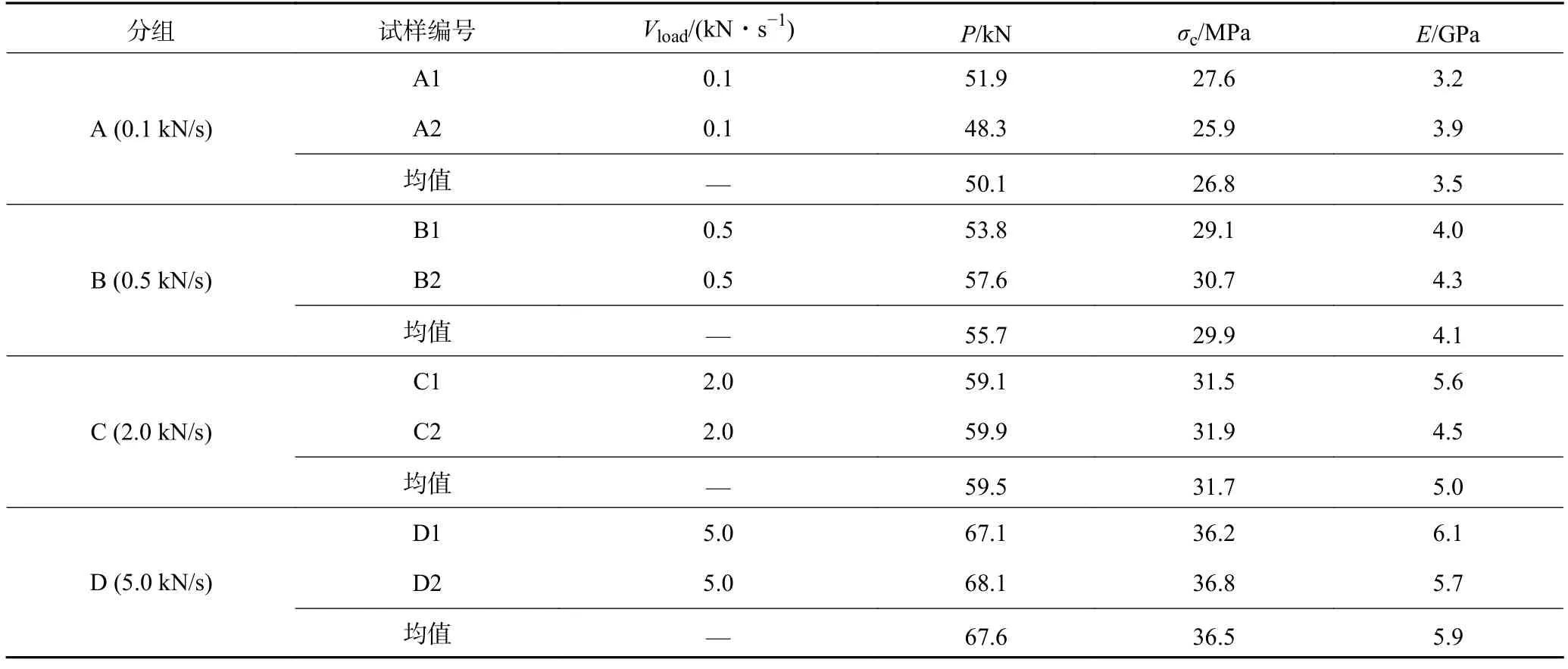
表2 不同加载速率下泥岩岩石强度测试结果Table 2 UCS test results of mudstone specimens under different stress loading rates

3.2 应力-应变曲线

图8 为不同加载速率下各试样轴向与径向应力-应变曲线及其局部放大，由图8 可知，在不同的加载速率下，各试样轴向应变曲线属典型的塑-弹-塑性曲线，各试样有明显的微裂隙压密过程，加载速率越小，压密过程越明显，即曲线越平缓。进入弹性阶段后，加载速率越大，曲线斜率越大，即平均弹性模量越大。进入塑性变形阶段后，加载速率越大，塑性越不明显，加载速率为2.0、5.0 kN/s 的4 个试样屈服点不明显。

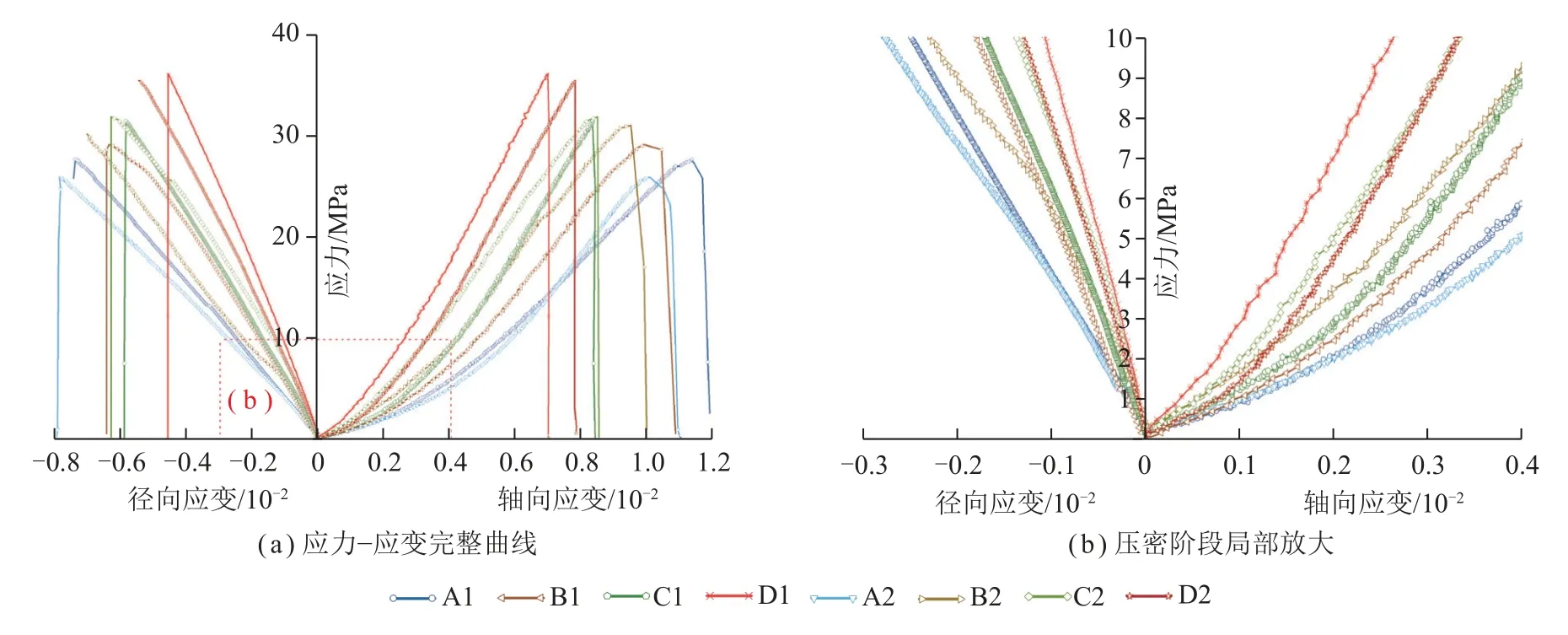
图8 不同加载速率下轴向与径向应力-应变曲线Fig.8 Stress-strain curves under different stress loading rates

3.3 强度特征

图9 为试验得到的单轴抗压强度σc、平均弹性模量E与试验加载速率Vload的关系曲线，由图8 和图9(a)可知，试验单轴加载速率与泥岩岩石单轴抗压强度有关联关系，加载速率越大，测试得到的泥岩岩石单轴抗压强度越大。加载速率由0.1 kN/s 增至50倍至5.0 kN/s 时，试验得到的平均单轴抗压强度由26.8 MPa 增大至36.5 MPa，强度增加了36.2%。由图8 和图9(b)可知，试验单轴加载速率和测试得到的岩石平均弹性模量有关联关系，加载速率越大，测试得到的岩石平均弹性模量越大。加载速率由0.1 kN/s增至50 倍至5.0 kN/s 时，试验得到的平均弹性模量由3.5 GPa 增大至5.9 GPa，增大了65.6%。由此可知，泥岩岩石强度参数有应力加载速率依赖性。由图9可知，单轴压缩强度、平均弹性模量与试验加载速率均为幂函数关系，荷载加载速率越大，单轴压缩强度、平均弹性模量变化率越小，数值越趋于稳定，即加载速率越大，其对2 者的影响越小。

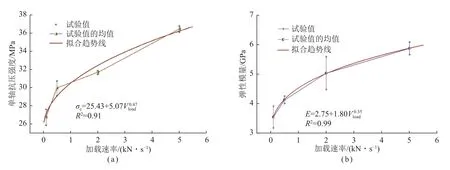
图9 单轴抗压强度、平均弹性模量与加载速率关系曲线Fig.9 Relationship curves between σc,E and Vload

3.4 轴向与径向应变特征

表3 为试验得到的不同加载速率下4 组试样轴向与径向应变特征表(表中εa,max为试样轴向应变最大值，εd,max为试样径向应变最大值)。图10 为试验得到的单轴压缩最大轴向应变、最大径向应变与试验加载速率的关系曲线，由图10 可知，泥岩岩石的轴向、径向应变和试验加载速率有关联关系，加载速率越大，测试得到的最大轴向应变和最大径向应变均越小，轴向和径向应变率均越大，即加载速率越大，泥岩岩石在未充分变形的情况下即发生破坏的可能性越大。当试验加载速率由0.1 kN/s 增大至0.5、2.0、5.0 kN/s 时，即增大5、20、50 倍时，最大轴向应变分别减小了0.071、0.203、0.313，最大径向应变分别减小了0.119、0.206、0.344，两者之间并非线性关系。轴向、径向应变值与试验加载速率均为幂函数关系，荷载加载速率越大，应变值变化率越小，数值越趋于稳定，其对轴向、径向应变的影响越小。

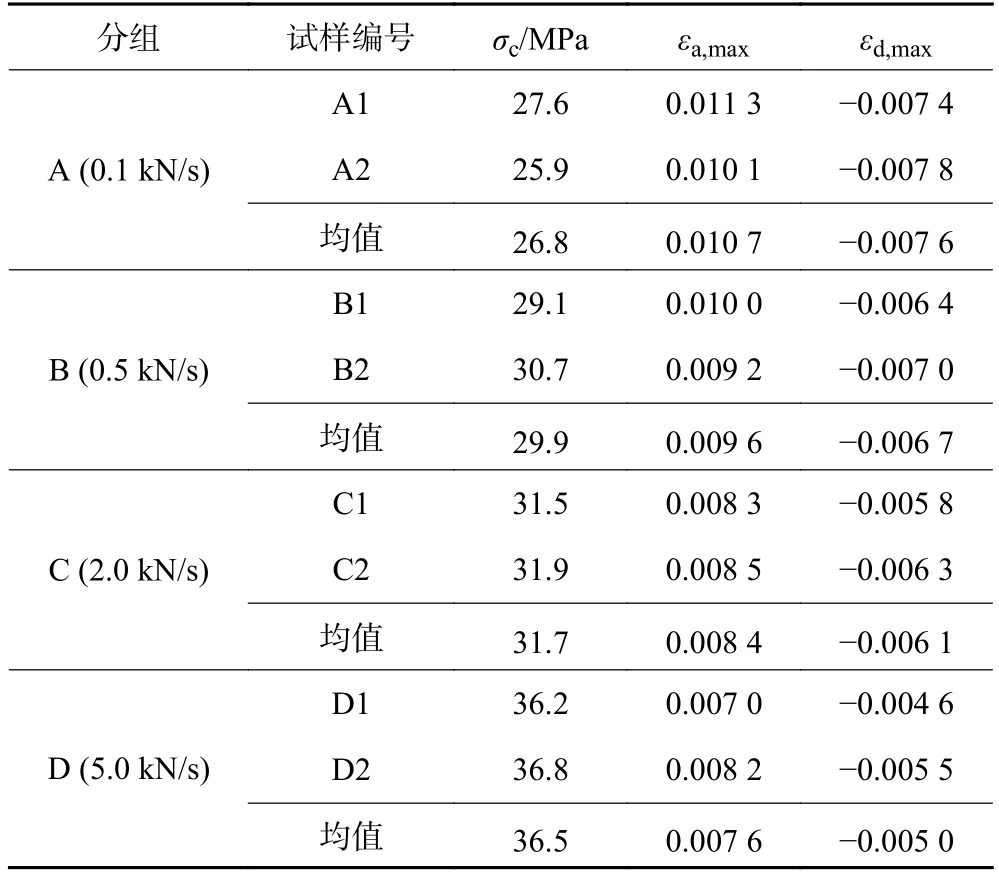
表3 不同应力加载速率下轴向与径向应变特征Table 3 Axial and radial strain characteristics under different stress loading rates

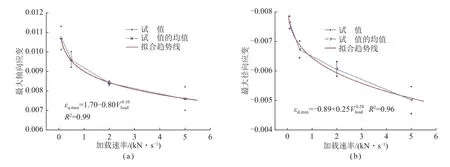
图10 最大轴向应变、最大径向应变与加载速率关系曲线Fig.10 Relationship curve between εa,max,εd,max and Vload

4 体积扩容特征

4.1 试验结果

根据ISRM 推荐方法“测定岩石材料在单轴压缩下变形性质的方法”[39]，在给定应力水平情况下，体积应变由式(1)计算

式中，εV为体积应变；εa为轴向应变，一般压缩为正值；εd为径向应变，径向膨胀一般为负值。

本试验在0.1、0.5、2.0 和5.0 kN/s 等4 种不同加载速率下8 个泥岩试样体积扩容测试计算结果见表4，由表4 可知，4 组泥岩岩石试样最大体积应变均值为-0.004 6，最大体积应变均值最小为-0.002 7，扩容起始应力与单轴抗压强度比值均值最大为0.205，均值最小为0.123。

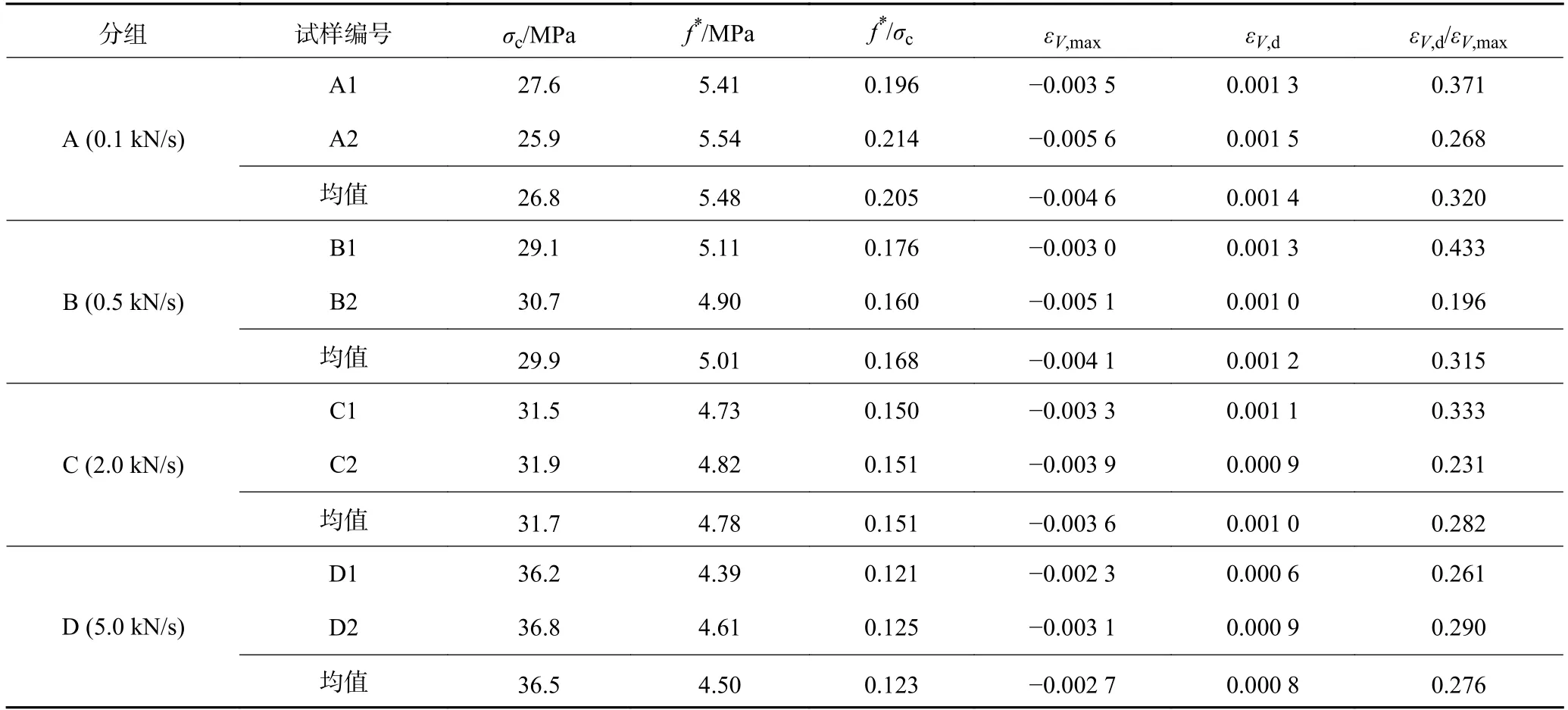
表4 不同应力加载速率下试样体积扩容特征Table 4 Characteristics of dilatancy under DSLR

4.2 应力-体积应变曲线

各试样不同加载速率下应力-体积应变曲线如图11 所示，可知在不同的加载速率下，各试样均表现出了体积扩容特性，试样在加载初期体积减小，体积在短时稳定后，即进入扩容阶段，扩容现象直至试样破坏方才结束。由图11 可知，荷载加载初期，试样在压密阶段时，各试样应力-体积应变曲线的斜率均很小，试样的体积应变急剧增大，即试样的体积处于急剧收缩阶段，此阶段试样体积收缩的主要原因是试样内容孔隙闭合，而径向应变较小。此阶段岩石应力-体积应变关系是近似线性的，岩石表现出黏-弹性性状。压密阶段后期，随着径向应变的增大，应力-体积应变曲线进入非线性阶段，各试样的体积进入到短时稳定阶段，即体积稳定的阶段。进入弹性阶段后，荷载应力达到一定的极限即扩容起始应力后，应力-体积应变曲线开始反转，泥岩岩石此时体积开始膨胀，即发生扩容现象。进入塑性变形阶段后，应力-体积应变曲线斜率减小，即试样处于加速扩容阶段，加载速率越大，线性斜率减小越明显，直至试样破坏。

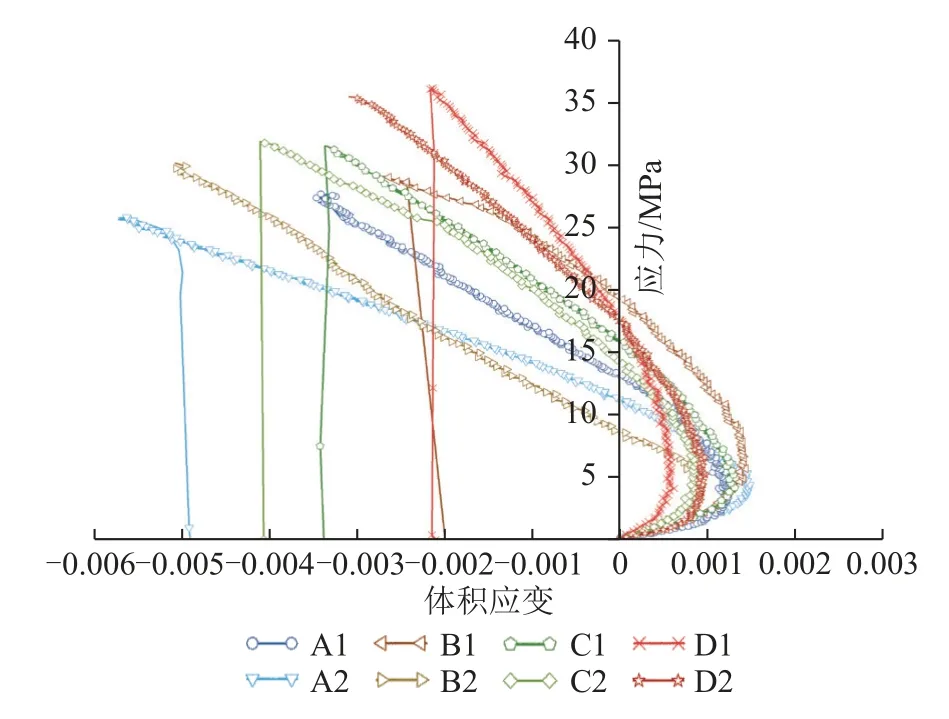
图11 不同加载速率下体积应变曲线Fig.11 Volume strain curves at different loading rates

4.3 体积扩容特征与加载速率关系

图12(a)为8 个试样最大体积应变与加载速率关系曲线，图12(b)为扩容起始体应变与最大体积应变比值与加载速率关系曲线。由表4 可知，4 组试样的扩容起始时体积应变与最大体积应变比值εV,d/εV,max均值最大为0.32(0.1 kN/s)，最小比值为0.276(5.0 kN/s)，最大比值是最小比值的1.16 倍。为了分析各组数据之间的差异显著性，分别选择置信区间为95%和90%，采用单因素方差分析的方法对各组最大体积应变数据、扩容起始体应变与最大体积应变比值数据进行了差异性分析，分析结果为各组数据差异性不显著。据此认为，试样最大体积应变、扩容起始体积应变与最大体积应变比值和加载速率无关联关系。

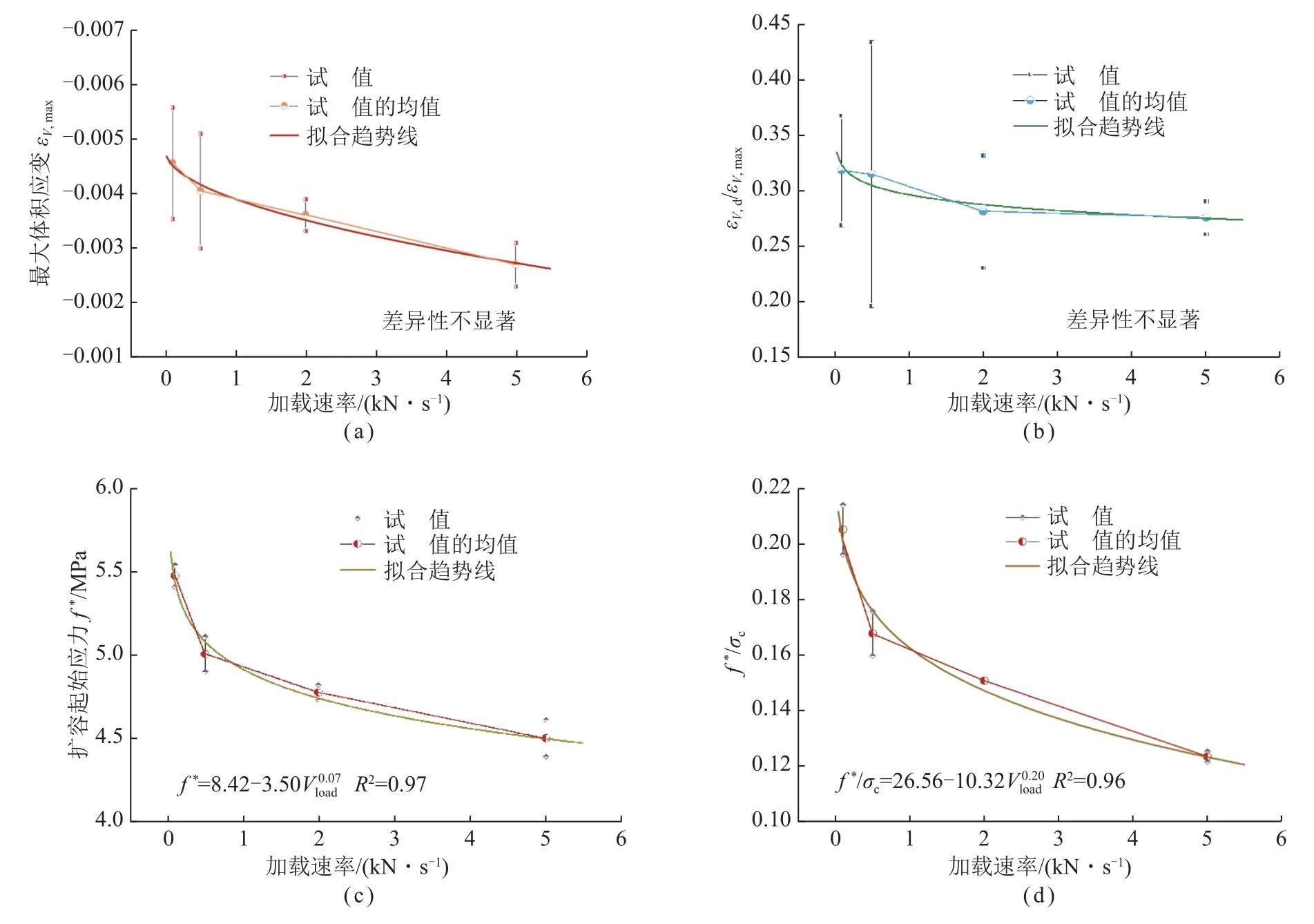
图12 体积扩容特征与加载速率关系曲线Fig.12 Relationship curves between volume dilatancy characteristics and Vload

图12(c)为各试样扩容起始应力f*与加载速率关系曲线，图12(d)为各试样扩容起始应力与单轴抗压强度比值f*/σc与加载速率关系曲线，由图12(c)、(d)可知，扩容起始应力、试样扩容起始应力与单轴抗压强度比值和加载速率有关联关系，加载速率越大，扩容起始应力越小，试样扩容起始应力与单轴抗压强度比值也越小，即试样加载荷载速率越大，越容易进入体积扩容阶段。

5 讨论

5.1 加载速率影响下扩容本构模型

TAN T 等[40]提出了与时间有关、考虑岩石扩容影响的岩石本构模型：

式中，e(t)ij为与时间有关的总应变；eeij为弹性应变；ec(t)ij为蠕变应变；edij为瞬时扩容应变；ed(t)ij为与时间有关的扩容应变；i、j为应变方向，取值为1、2、3，1为竖向，2 为竖平面法线横向，3 为竖平面横向。

若不考虑时间的影响，式(2)可改写为

岩石压缩试验时，体积总应变e、弹性体积应变ee和扩容体积应变ed可表示为

式中，ee1和ee3分别为竖向弹性应变和径向弹性应变；ed1和ed3分别为竖向扩容应变和径向扩容应变。

竖向总应变e1可表述为竖向弹性应变和竖向扩容应变和，径向总应变e3可表述为径向弹性应变和径向扩容应变和：

根据虎克定律，式(3)中弹性应变eeij分解为ee1和ee3，可表述为

式中，E为平均弹性模量；μ为岩石泊松比；Δσx和Δσy分别为x方向和y方向应力变化量。

将瞬时扩容应变edij的表达式进行简化后，得到

式中，D*、C、n为扩容常数，由试验获得；f*为扩容起始应力；σ1和σ3分别为最大主应力和最小主应力。

由上文分析可知，试样的加载速率对岩石的平均弹性模量E和扩容起始应力f*均有影响，由式(9)～(14)可知，平均弹性模量是弹性应变的计算因子，扩容起始应力是扩容应变的计算因子，加载速率对弹性应变和扩容应变均有影响。加载速率和平均弹性模量E、扩容起始应力f*均为幂函数关系，其关联函数表达式为

其中，aE、bE、cE为拟合加载速率和平均弹性模量关联方程式常数参数；af、bf、cf为拟合加载速率和扩容起始应力关联方程式常数参数，上述常数参数均为正值，均由试验数据回归分析时非线性曲线拟合得到。

将式(15)代入式(9)～(11)，得到应力加载速率影响下的弹性本构模型：

将式(16)代入式(12)～(14)，得到加载速率影响下的瞬时扩容本构模型：

将式(17)～(22)中对应的轴向应变、径向应变、总应变分别相加，得到应力加载速率影响下岩石变形本构模型：

5.2 加载速率与强度参数、变形参数关系

笔者将试验荷载加载速率与试样试验单轴抗压强度、平均弹性模量等强度特征参数及轴向与径向应变、体积扩容等应变特征参数进行拟合，拟合形式采用下述幂函数表达式：

式中，k为各试验结果计算得到的参数；v为试验荷载加载速率，kN/s；a、b、c为拟合方程式常数参数。

对方程式(26)两侧取对数，可得

由式(27)可知，荷载加载速率对数值与各强度参数和应变特征参数对数值为线性关系。

在对上述试验数据进行拟合之前，采用单因素方差分析方法对每个分析项目各组数据进行了差异显著性检验，选择置信区间为95%，若差异显著则对数据进行拟合。差异显著性分析结果和拟合计算结果见表5。

表5 试验荷载加载速率与试验参数拟合结果Table 5 Fitting results of Vload and test parameters

由表5 中差异显著性计算结果可知，试验加载速率和泥岩岩石单轴抗压强度、平均弹性模量、最大轴向应变、最大径向应变、试样扩容起始应力与单轴抗压强度比值有关联关系，和试样最大体积应变值、扩容起始体积应变与最大体积应变比值无关联关系。

由以上分析可知，试验荷载加载速率与强度特征参数及应变特征参数之间为幂函数关系，幂函数的特点是在自变量较小时，因变量随自变量变化而发生较大变化，即相应的关系曲线斜率较大。随自变量持续增大，因变量斜率变缓。针对本文各试验而言，加载速率在1 kN/s 及以下时，加载速率越小，试验得到的数据变化速率越大，加载速率越大，数据稳定性越好。

6 结论

(1)试验发现泥岩以主要含有长石、石英、绿泥石等矿物，以长石为主，占比达到43.1%，岩石内部各矿物成分分布不均匀，长石呈条带状分布，其间填充其他矿物，各种矿物的分布表现出了强烈的非均质性，该性质是岩石表现出各向异性的主要原因。

(2)各试样在不同的加载速率下，轴向应力-应变曲线均属典型的塑-弹-塑性曲线，各试样均有明显的微裂隙压密过程，加载速率越小，压密过程越明显，即曲线越平缓。进入弹性阶段后，加载速率越大，曲线斜率越大，即平均弹性模量越大。

(3)采用单因素方差分析方法对每个分析项目各组数据进行差异显著性检验，结果为试验加载速率和泥岩单轴抗压强度、平均弹性模量、最大轴向应变、最大径向应变、扩容起始应力与单轴抗压强度比值有关联关系，和最大体积应变、扩容起始体积应变与最大体积应变比值无关联关系。加载速率越大，试样在未充分变形的情况下发生破坏的可能性越大，扩容起始应力越小，试样扩容起始应力与试样强度比值也越小，越容易进入体积扩容阶段。

(4)各试样在不同的加载速率下，均表现出明显的体积扩容特性。荷载加载初期，各试样在压密阶段时，应力-体积应变曲线的斜率较小，即试样的体积快速减小。进入弹性阶段后，荷载应力达到扩容起始应力后，应力-体积应变曲线开始反转，试样体积开始膨胀。进入塑性变形阶段，曲线斜率减小，试样处于加速扩容阶段至试样破坏。