水-力耦合作用下砂岩力学特性与能量演化及强度准则适用性分析

2023-10-18赵延林张春阳张英杰吴连华

煤炭学报 2023年9期

赵延林，谭涛，张春阳, ，刘强，张英杰，吴连华

(1.湖南科技大学资源环境与安全工程学院,湖南湘潭 411201；2.煤炭资源清洁利用与矿山环境保护湖南省重点实验室,湖南湘潭 411201；3.武汉理工大学资源与环境工程学院,湖北武汉 430070；4.金属矿山安全与健康国家重点实验室,安徽马鞍山 243003；5.中钢集团马鞍山矿山研究总院股份有限公司,安徽马鞍山 243003)

岩石的水-力耦合特性是岩土工程领域的一个重要热点问题[1-4]。目前许多学者对水-力耦合下岩石强度和变形特征进行了大量研究。BROUO 等[5]结合理论和试验方法，讨论了孔隙水压力对结晶岩中拉伸裂缝起裂和扩展方向的影响。IVARS[6]通过三维流体力学数值模拟研究了裂隙岩体开挖水体渗入的问题。朱珍德等[7]使用MTS 岩石力学试验系统对花岗岩进行了不同围压和渗透水压的三轴压缩试验，研究脆性岩石的全应力-应变过程中的渗流特性。刑福东等[8]研究了高围压高水压作用下脆性岩石的三轴力学特性，对脆性岩石的变形和脆-延性转化进行了讨论。唐春安等[9-10]通过孔隙水压作用下岩石破坏过程的数值模拟，研究了孔隙水压力对岩石中裂纹扩展的影响。李玉寿等[11]对煤样进行了孔隙水压力作用下岩石的三轴压缩试验，讨论了水-力耦合作用下岩石的声学特征。刘刚等[12]对黄砂岩进行单、三轴以及孔隙水作用下的力学试验，研究岩石损伤破坏过程中的力学行为，并基于能量损伤演化方程描绘了损伤演化的5 个阶段，得到孔隙水压与岩石脆性损伤之间的关系。

岩石的强度准则是岩土理论的一个重要组成部分，对巷道、硐室、边坡等工程的初步设计具有重要的指导意义。水-力耦合作用下岩石破坏机制更为复杂，该状态下经典强度准则能否准确描述岩石强度的变化规律，是深部地下开采工程需要解决的重要问题[13]。自1923 年TERZAGAHI[14]基于工程实践经验提出了饱和土的有效应力原理以来，部分学者将有效应力原理结合经典的岩石强度准则，探讨了水-力耦合下岩石峰值强度随外部应力和孔隙水压的变化规律。如，许江[15-17]、赵延林等[18-19]发现水-力耦合作用下砂岩和裂隙灰岩峰值强度的变化规律符合Mohr-Coulomb 准则。由上可知，水-力耦合下岩石的强度参数、变形参数以及裂隙扩展等方面的研究已取得了丰富的成果。但是关于水-力耦合下岩石的能量变化规律的研究较少。水-力耦合作用下岩石内部孔隙水压力对其固体骨架的作用不容忽略，该状态下岩石能量演化规律还需要进一步分析。此外，根据不同岩性强度不一的特点，水-力耦合下岩石强度的变化规律尤其是破坏后的残余强度还需要深入探讨。

基于此，笔者开展三轴压缩条件下砂岩水-力耦合试验，获取不同孔隙水压下砂岩的应力-应变曲线，得到水-力耦合下岩石归一化强度衰减方程，讨论了岩石能量变化规律；最后，结合已公开发表的试验结果，基于TERZAGAHI 有效应力原理，对水-力耦合下不同岩石的有效峰值强度，有效残余强度与有效围压的关系进行了讨论，验证Mohr-Coulomb 准则和Hoek-Brown 准则的适用性。

1 试验方法

1.1 试件制备

以河北省滦南县马城铁矿矿区埋深为420～500 m段的砂岩为研究对象，将采集到的岩样按GB/T 23561.1—2009《煤和岩石物理力学性质测定方法》的要求对其进行加工[20]，制备成φ50 mm×100 mm 的标准圆柱体试件，如图1 所示。按照水利水电试验规程SL/T246—2020 对标准砂岩试样进行饱水处理[21]。在试验规程中，岩石强制饱水后，每隔2 h 对浸没于水中的试件称重，当相邻2 次的质量相差不超过0.01 g 时，可认为试件已充分饱水，测得该砂岩试件的饱和吸水率在6.67%左右。

图1 标准砂岩试件Fig.1 Standard sandstone specimens

通过AniMR-150 核磁共振(NMR)测试系统获得3 个具有代表性的砂岩试件的T2谱分布。根据核磁弛豫机理，不同类型岩石孔隙中的流体具有不同的弛豫时间，分布在T2谱曲线上的不同位置，根据T2值与孔径r的对应关系，可以将 T2谱曲线转换为孔径分布曲线，如图2 所示。

图2 孔隙度分量以及累计孔隙度与孔径的关系Fig.2 Porosity distribution and cumulative porosity versus pore diameter

由图2 可知，砂岩孔径分布曲线呈三峰形，不同的峰对应不同的孔类型：从左到右的第1 个、第2 个和第3 个峰分别表示微孔、中孔和大孔，其中大孔贡献的孔隙度约占51.3%，而中孔和微孔贡献的孔隙度分别约为32.9%和15.8%。NMR 测试系统获得该砂岩试件的平均孔隙度为14.28%。这表明：该砂岩试件为高孔隙性岩石，且具有发达的大孔隙结构，试件的基本信息见表1。

表1 试件基本物理力学参数Table 1 Basic physical and mechanical parameters of specimens

1.2 试验装置和程序

水-力耦合作用下砂岩三轴压缩试验在湖南科技大学岩石力学实验室的MTS815 岩石力学试验系统上进行，该试验系统所配备的轴压、围压和孔隙水压均为独立的伺服控制系统，其中水压伺服系统包含有水箱，控制阀门和水压监测系统。试验过程中水压监测系统伺服运行，从而保证试件处于恒定水压状态，如图3(a)所示。MTS815 试验系统由加载系统、控制器、测量系统等部分组成。加载系统包括液压源、载荷框架、作动器、伺服阀、三轴试验系统、孔隙水压试验系统及温度试验系统。主要技术参数有：最大轴向力4 600 kN，最大轴向拉力2 300 kN，最大围压140 MPa，最大孔隙水压力140 MPa。设备可以自动采集试验过程中的轴向载荷、围压、孔隙水压、轴向位移、环向位移和时间等数据。

图3 MTS815 岩石力学试验系统Fig.3 MTS815 rock mechanics test system

先用热缩管将试件环向包裹，试件上下端面通过压盘上的上下进水口与外部水压伺服系统相连，然后将其放置于试验系统底座，安装好环向引伸计、轴向引伸计和导水管，如图3(b)所示。三轴压缩试验围压σ3设定为10、20 和30 MPa 等3 种情况，每个围压下，按照孔隙水压与围压的比值(即孔围比)P/σ3分别为0、0.1、0.2、0.4、0.6、0.8 和0.9，共设置7 种孔隙水压P。具体试验程序如下：①以0.05 MPa/s 的加载速率同时加载轴向应力σ1和围压σ3到试验设计值，使试件达到三轴静水压力的状态(σ1=σ2=σ3)；②以0.05 MPa/s 的加载速率加载孔隙水压P至设计值，并维持20 min；③采用位移控制的方式对试件进行轴向偏应力加载，加载速率为0.1 mm/min[16-17]，直到试件破坏并进入残余阶段，试验加载路径如图4 所示。

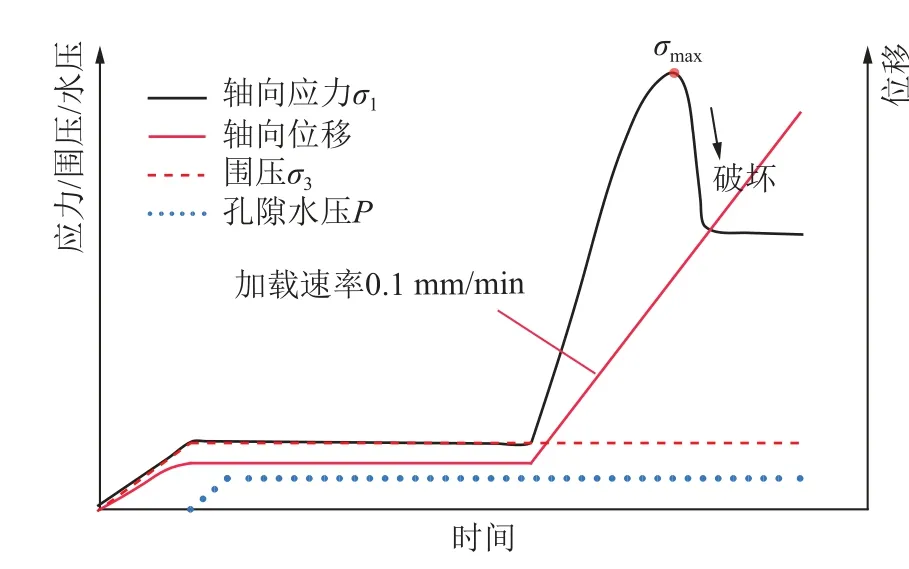
图4 试验加载过程示意Fig.4 Schematic diagram of test loading paths

2 水-力耦合下砂岩的力学特性

2.1 变形特性分析

图5 为水-力耦合作用下砂岩试件应力-应变曲线。水-力耦合作用下三轴压缩试验的应力-应变曲线均经历了5 个阶段，即原生裂隙压缩闭合阶段(OA段)、线弹性阶段(AB段)、裂纹稳定扩展阶段(BC段)、裂纹不稳定发展阶段(CD段)和峰后阶段[22]。在不同围压和孔隙水压的作用下，试件的应力-应变曲线基本一致，都随着轴向位移的增大，试件的偏应力增大至峰值，然后迅速跌落，进入残余阶段。

图5 水-力耦合下砂岩的应力-应变曲线Fig.5 Stress-strain curves of sandstone under hydro-mechanical coupling

为研究水力耦合作用下岩石的变形特征，取峰值偏应力20%～60%范围线弹性阶段的斜率为弹性模量E，该段环向应变与轴向应变的比值为泊松比v，即

式中，σA、σB分别为图5 中曲线弹性阶段起点和终点对应轴向应力，其对应的轴向应变分别为ε1A和ε1B。

以孔围比(P/σ3)作为特征参数，探讨变形、强度参数和孔围比之间的相依关系，图6 为水-力耦合作用下砂岩的弹性模量和泊松比。

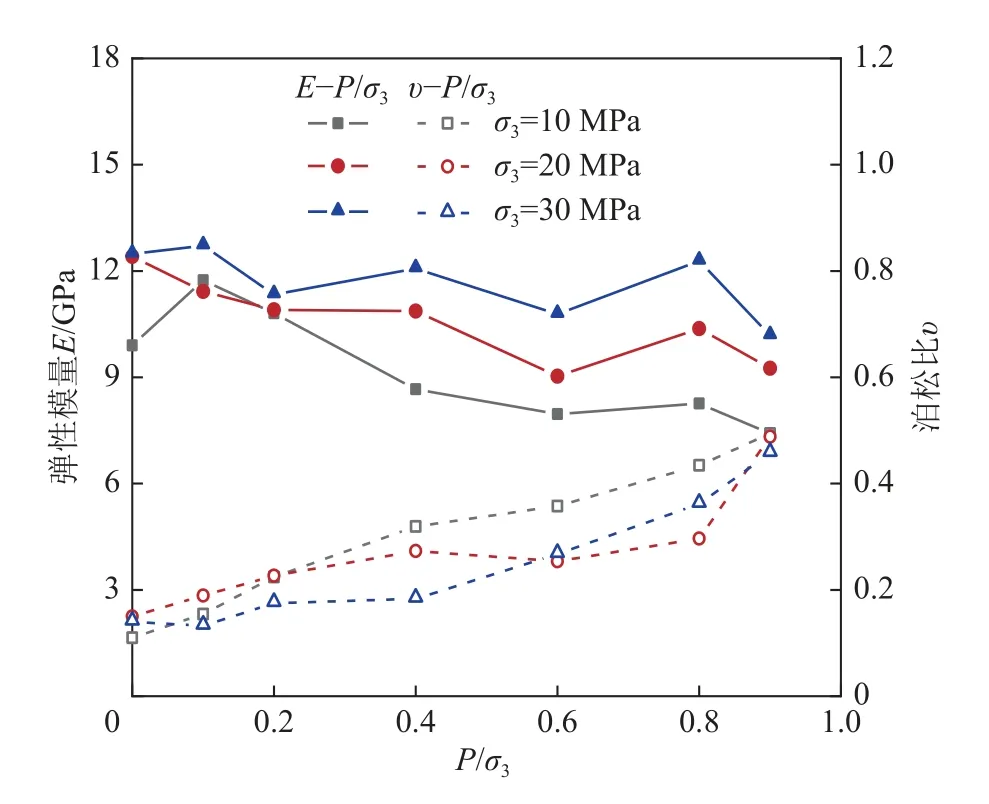
图6 试件的弹性模量和泊松比Fig.6 Elastic modulus and Poisson’s ratio of specimens

由图6 可知，除去个别离散的试件，水-力耦合作用下砂岩的弹性模量E与P/σ3呈负相关关系，而泊松比v与P/σ3呈正相关关系。

2.2 强度特性分析

根据图5 的应力-应变曲线，获得水-力耦合下砂岩的峰值强度和残余强度，见表2。

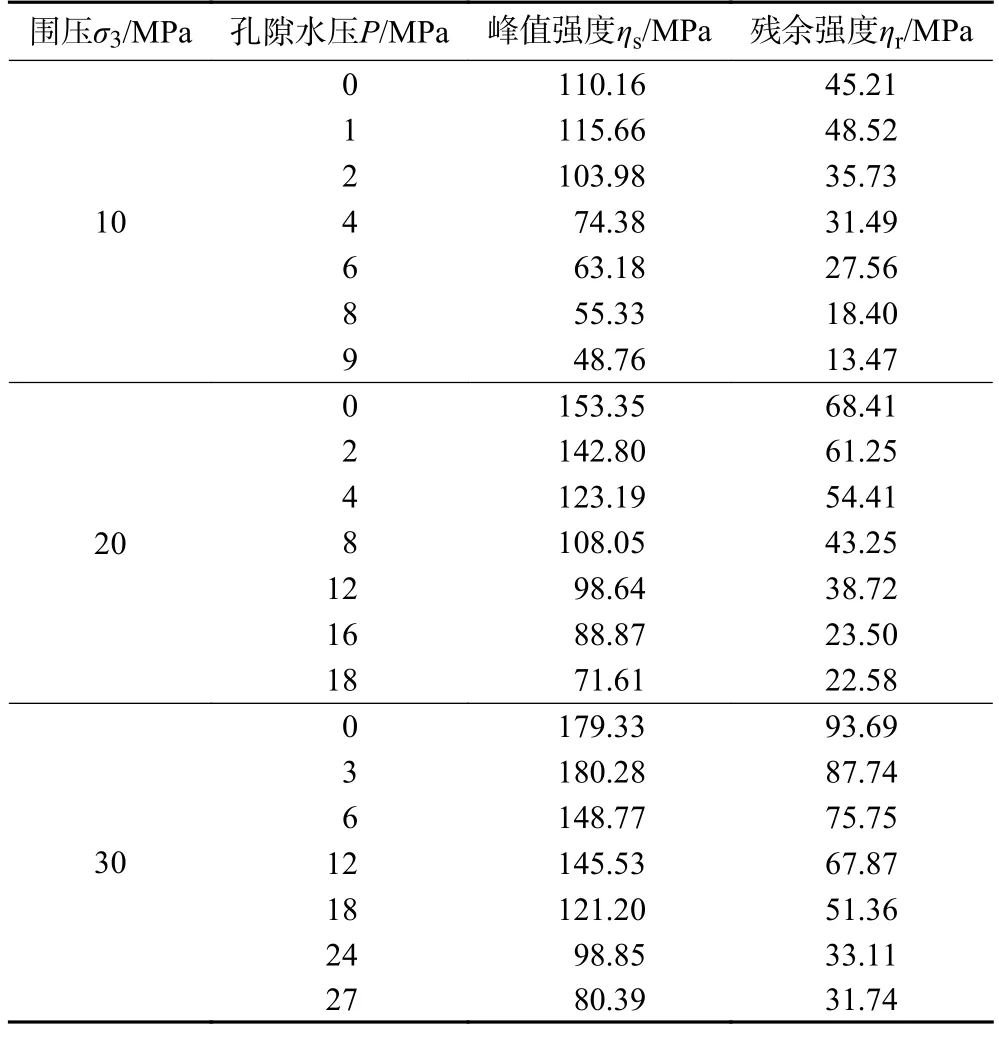
表2 砂岩的峰值强度和残余强度Table 2 Peak strength and residual strength of sandstone

从表2 可以发现：砂岩峰值强度和残余强度受到孔隙水压和围压的共同影响，在相同的围压下，试件峰值强度随着孔隙水压的增大而减小；相同孔隙水压下，试件峰值强度和残余强度随着围压的增加而增大。

用水-力耦合下砂岩的峰值强度和残余强度除以围压单独作用下的对应值，获得水-力耦合下岩石归一化峰值强度ηs和归一化残余强度ηr。

式中，σp与σr分别为水-力耦合作用下岩石的峰值强度和残余强度；σp0与σr0分别为相应围压下无孔隙水压时岩石的峰值强度和残余强度。

类似地，以孔围比(P/σ3)作为特征参数，探讨归一化峰值、残余强度与孔围比的相依关系。图7 为归一化峰值ηs、残余强度ηr与孔围比P/σ3的关系曲线，发现ηs、ηr随着P/σ3的增加线性减少。

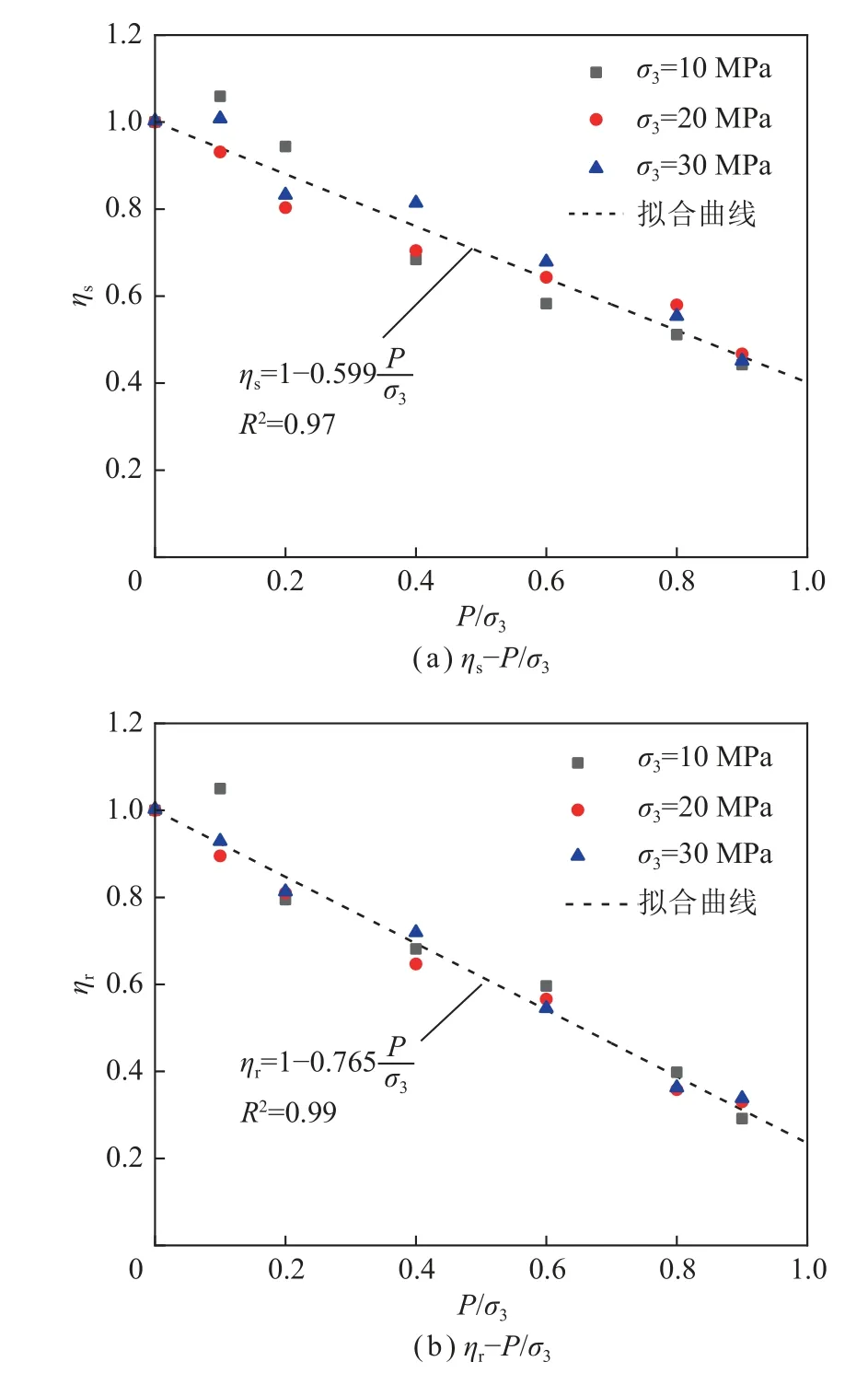
图7 归一化峰值强度、残余强度与孔围比的关系Fig.7 Relationship between normalized peak and residual strength and ratio of pore water pressure to confining pressure

其中，ωs和ωr分别为峰值强度衰减系数和残余强度衰减系数。对于本试验砂岩的ωs和ωr分别为0.599 和0.765。

为进一步验证上述强度衰减方程对不同岩性的适用性，引用目前已发表的水-力耦合作用下大理岩、中细砂岩、煤、黄砂岩、细砂岩和花岗岩等岩样的试验结果[8,11-12,16,23-25]，并使用强度衰减方程对其进行拟合，如图8 所示。由于部分岩石试验数据不全，残余强度的衰减分析中只包含煤[11]和黄砂岩[12]2 种岩石(图8(b))。

图8 不同岩石的强度衰减方程Fig.8 Strength reduction equations for different rocks

从图8 可以发现，本试验获得的强度衰减方程对于不同岩石同样适用。但是不同岩石的强度衰减系数不一样，从公开发表的文献来看,基于孔围比P/σ3，水-力耦合作用下岩石峰值强度衰减系数ωs介于0.332～0.599,残余强度衰减系数ωr介于0.650～0.765。而且发现岩石残余强度衰减系数ωr始终大于峰值强度衰减系数ωs，说明相对于峰值强度，残余强度受到孔隙水压的影响更大。

2.3 破坏模式

试件的破坏模式是反映其破坏机理的关键特征，水-力耦合下砂岩的破坏模式如图9 所示。从图9 可以发现：水-力耦合下砂岩主要发生剪切破坏，其破坏程度随着P/σ3的增大而愈发显著，当P/σ3较低时，试件剪切面单一，产生裂纹较少，随着P/σ3的增大，水力致裂愈发显著，试件同时发生剪切破坏和轻微的轴向劈裂。

总结发现：当围压恒定时，试件的破裂角在整体上随着P/σ3的增大而增大。例如，在围压30 MPa 的情况下，当P/σ3从0.1 增大至0.9 时，砂岩的破裂角由60°增加到79°(图9(c))。当P/σ3较低时，试件破坏需要更大的偏应力，岩石的内摩擦作用更加明显，抑制了岩石的断裂，使得破裂角变小。而随着P/σ3的增大，砂岩内部的孔隙水压力变大，有效围压和约束能力降低，削弱了内摩擦作用，因而出现破裂角较大的断裂面。

3 水-力耦合作用下砂岩能量演化规律分析

3.1 能量计算方法

在水-力耦合作用下的三轴压缩试验过程中，试验机对试件所做的功是为总输入能W,根据热力学第一定律[26]可得

式中，Wd为耗散能，主要是岩石内部损伤和塑性变形产生；We为弹性能，该部分的能量主要由岩石弹性变形产生。

在三轴压缩试验中，从初始状态到静水压力状态，以及孔隙水压加载状态，试件内部也有能量演化，但考虑到该阶段能量变化较小，对岩石的破坏影响较低，笔者只考虑偏应力加载阶段的能量演化[12,27-28]。在偏应力加载阶段，岩石处于水-力耦合状态，内部的孔隙水压力会使岩石固体骨架发生变形而做功，作用方向与外部加载应力的作用方向相反，此时总输入能密度U、弹性能密度Ue和耗散能密度Ud分别为

式中，ε1t和ε3t分别为偏应力-应变曲线对应的时刻轴向应变和环向应变。

3.2 能量演化曲线

结合式(5)～(7)和图5 获得水力耦合作用下饱水砂岩的能量演化曲线。研究发现水-力耦合作用下饱水砂岩在全应力-应变过程中的能量演化曲线的趋势基本一致，下面以10 MPa 围压条件下孔隙水压为2 MPa 时饱水砂岩的能量演化曲线为例，讨论水-力耦合作用下岩石的能量变化，如图10 所示。

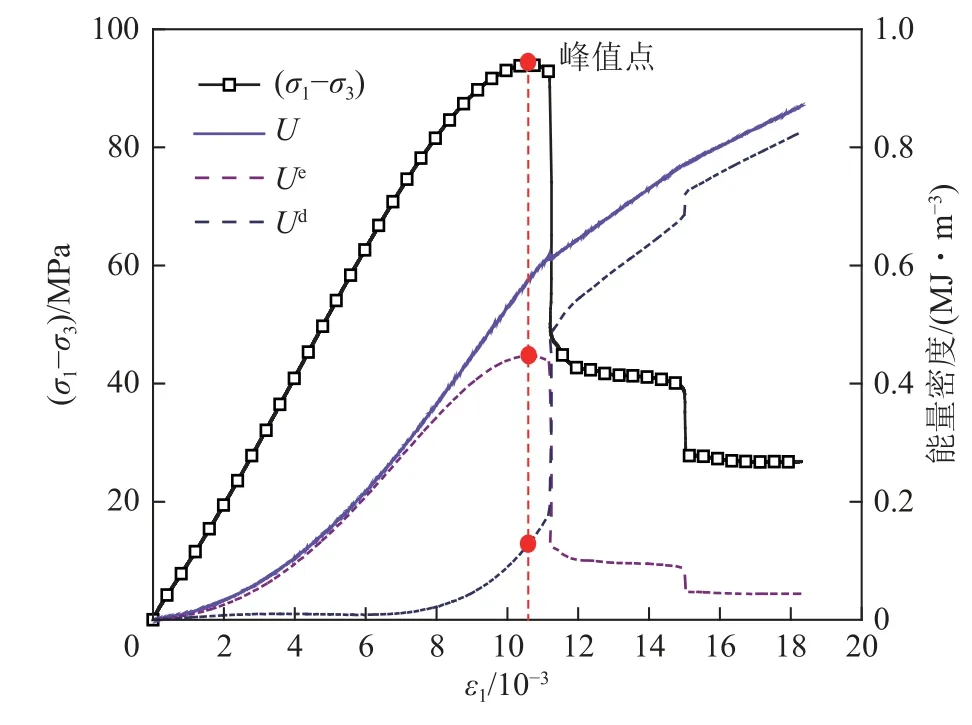
图10 水-力耦合作用下饱水砂岩的能量演化曲线Fig.10 Energy evolution curves of water-saturated sandstone under hydro-mechanical coupling

从图10 可以看出，水-力耦合作用下的能量变化曲线具有相同的趋势：峰值前阶段，饱水砂岩的总输入能密度、耗散能密度和弹性能密度均随着轴向应变的增加而逐渐增大，其中耗散能密度一直处于较低的水平，表明岩石在峰前阶段主要发生能量积聚能量耗散较少。而弹性能密度的增速呈现先加速增长后减速增长的趋势，这是因为在偏应力的作用下，岩石主要发生弹性变形，积聚大量弹性能，弹性能密度大幅增加；而临近破坏时，岩石内部结构发生改变，岩石裂隙不稳定扩展，此时孔隙水压进入裂隙内部以张力的形式作用于裂隙两侧和尖端，促使裂隙进一步发育，表面能增多，砂岩弹性能的积聚速度下降。峰后阶段，岩石迅速破坏弹性能大量释放，弹性能密度急剧减少，而耗散能密度快速增大。由于围压约束作用，破坏后试件内部仍储存有少量的弹性能。

3.3 特征能量

图11 水-力耦合作用下饱水砂岩的储能极限和峰值耗散能Fig.11 Energy storage limitation and peak dissipation energy density of water-saturated sandstone under hydro-mechanical coupling

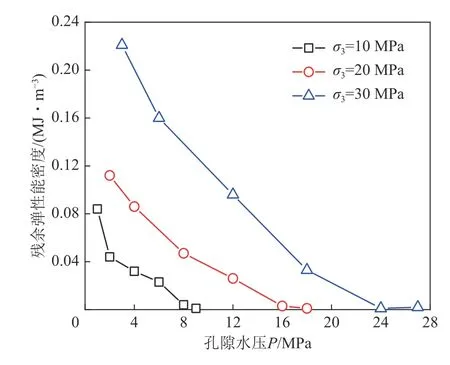
图12 砂岩的残余弹性能密度Fig.12 Residual elastic energy density of sandstone

3.4 能量变化率曲线

定义弹性能密度与总输入能密度的比值为弹性能率ηe，耗散密度能与输入能密度的比值为耗散能率ηd，来表征岩石能量积聚和释放的能力。同样地，以10 MPa 围压条件下孔隙水压为6 MPa 时饱水砂岩的弹性能率和耗散能率为例，如图13 所示。

图13 饱水砂岩的弹性能率 ηe 和耗散能率ηdFig.13 Elastic energy ratio ηe and dissi pation energy ratio ηd of water-saturated sandstone

由图13 可知，水-力耦合作用下，砂岩的弹性能率在试验过程中经历了非线性减小、近似线性增加、非线性增加、非线性减小、急剧减小和平缓减小等6个阶段，而耗散能率的变化与之相反。

以6 MPa 孔隙水压为例，当轴向应变由0 增加至6.8×10-4时，饱水砂岩处于全应力-应变曲线中原生裂隙压密阶段(O1A1段)，由于初始孔隙压密导致能量积聚水平下降，弹性能率从1.00 非线性减少至0.71。当砂岩处于弹性变形阶段时(A1B1段)，岩石内部主要发生能量积聚，其弹性能率呈现线性增大。随着轴向应变的继续增加，岩石内部裂隙开始衍生和扩展，岩石积聚的弹性能部分转化为耗散能，弹性能率的增长速度变慢，当增加至最大值0.95 时(c点)，砂岩进入裂纹不稳定扩展阶段(C1D1段)，其内部裂纹开始扩展，弹性能率下降，当弹性能达到储能极限时(d点)，试件内部宏观裂纹贯通释放大量能量，弹性能率迅速下降至0.07(e点)。最后，弹性能率在残余阶段呈现缓慢下降的趋势。随着孔隙水压的增大，饱水砂岩的峰值弹性能率在0.93～0.98 波动。试验发现，砂岩的残余阶段的弹性能率随着孔隙水压的增大而减小，表明孔隙水压加速岩石的能量耗散，降低了破坏后岩石结构的稳定性。

4 水-力耦合作用下岩石强度准则适用性分析

Mohr-Coulomb 准则和Hoek-Brown 准则是最为经典的2 个岩石强度准则，广泛使用于岩石力学理论分析与数值分析当中。天然岩石内部含有各种非连续缺陷，孔隙水压的存在会影响岩石的强度演化。此时，Mohr-Coulomb 准则和Hoek-Brown 准则的适用性值得探讨。

在对水-力耦合下岩石的强度进行分析时，根据有效应力原理得到岩石固体骨架的有效峰值强度、有效残余强度和有效围压[18-19]，分别为

4.1 Mohr-Coulomb 准则的适用性

由图14 可知，砂岩的有效峰值强度和有效残余强度的Mohr-Coulomb 准则拟合式的相关系数为0.93，表明水-力耦合下砂岩的峰值强度和残余强度随围压、孔隙水压的变化关系符合Mohr-Coulomb 准则。进一步地，用Mohr-Coulomb 准则对已发表的水-力耦合作用下大理岩、中细砂岩、煤、黄砂岩、细砂岩和花岗岩等岩样的试验结果进行分析(图14)，发现以上岩石的峰值强度和残余强度均满足Mohr-Coulomb 准则，R2＞0.83。这表明Mohr-Coulomb 准则适用于描述水-力耦合作用下岩石峰值强度和残余强度的变化规律。

图14 水-力耦合作用下不同岩石强度的Mohr-Coulomb 准则拟合曲线Fig.14 Fitting curves of Mohr-Coulomb criterion for the strength of different rocks under hydraulic-mechanical coupling

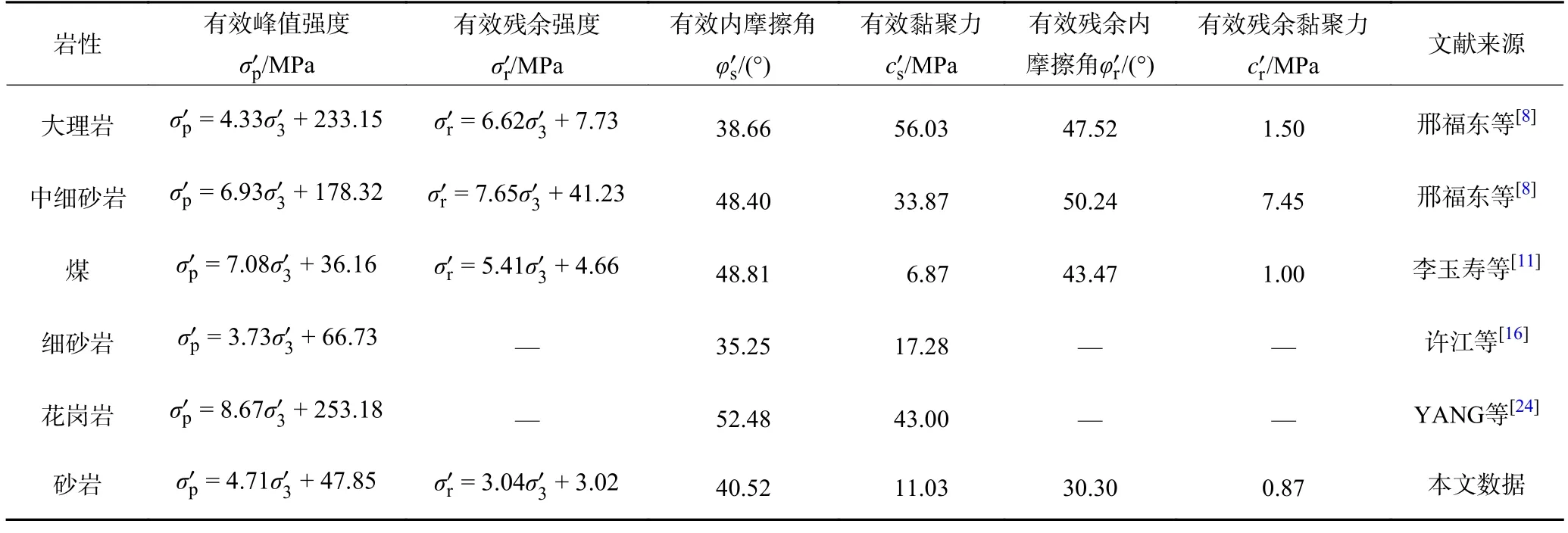
表3 Mohr-Coulomb 准则强度参数Table 3 Strength parameters of Mohr-Coulomb criterion

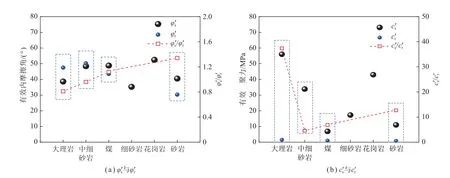
图15 Mohr-Coulomb 准则参数对比Fig.15 Comparison of Mohr-Coulomb criterion parameters

一般认为岩石的强度由黏聚强度和摩擦强度组成，其中，黏聚强度来自于岩石内部颗粒之间的黏聚力，摩擦强度来自于岩体内部颗粒摩擦和裂隙滑移[32-33]。岩石在峰后残余阶段其试件已经破坏，试件的黏结力大幅下降，出现有效残余黏聚力远远低于有效黏聚力的现象(图15(b))，岩石的残余强度归根于峰后阶段围压作用下试件破裂面摩擦咬合导致的摩擦。

4.2 Hoek-Brown 准则的适用性

式中，ms为峰值强度对应的经验参数；σc为岩石单轴抗压强度，本试验饱水砂岩的单轴抗压强度σc为29.75 MPa。

JUN PENG 等[32]认为Hoek-Brown 准则中岩石残余强度与其单轴抗压强度有关，并验证了其可靠性，即

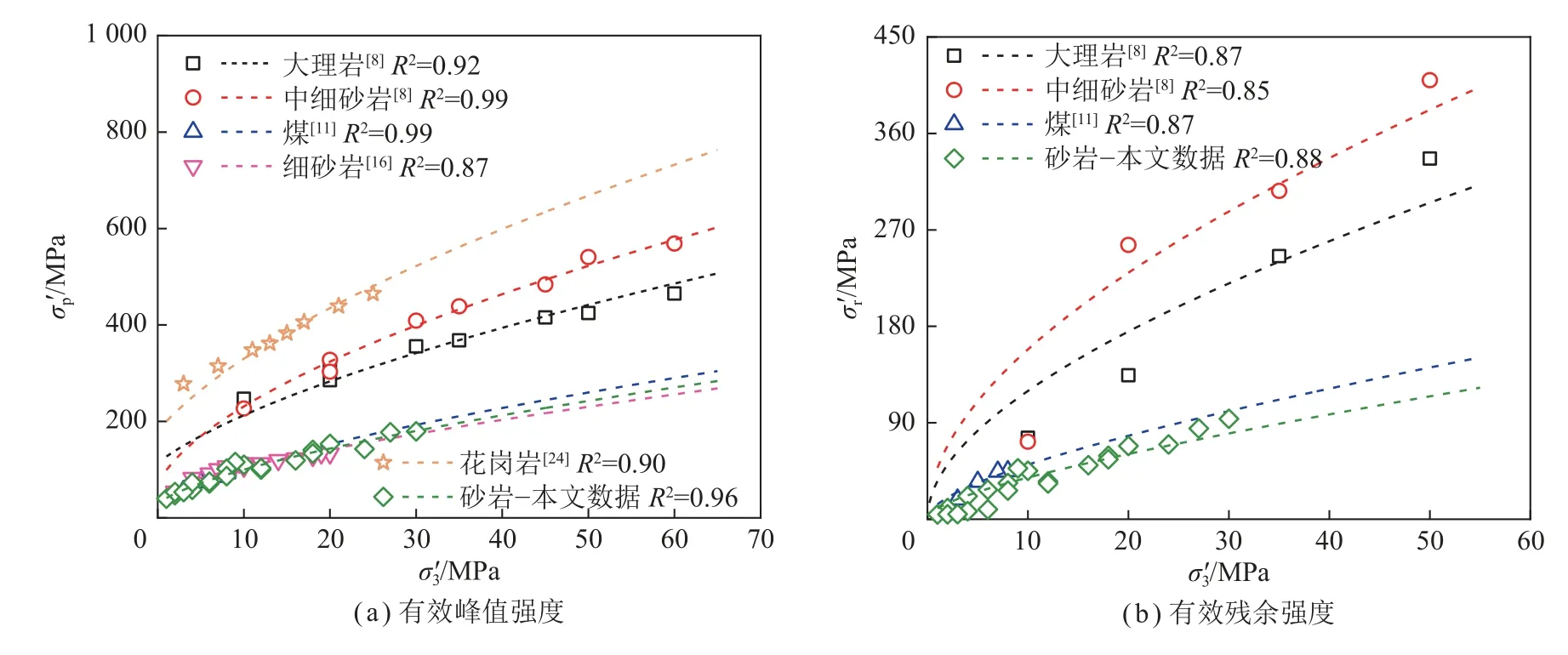
图16 水-力耦合作用下不同岩石强度的Hoek-Brown 准则拟合曲线Fig.16 Fitting curves of Hoek-Brown criterion for the strength of different rocks under hydraulic-mechanical coupling

从图16 可知，砂岩的Hoek-Brown 准则拟合式的相关系数均大于0.88，表明Hoek-Brown 准则表述水-力耦合作用下砂岩的峰值强度和残余强度与围压、孔隙水压的关系是合理的。

同样地，用Hoek-Brown 准则对已发表的水-力耦合下大理岩、中细砂岩、煤、黄砂岩、细砂岩和花岗岩等岩样的试验结果进行分析，如图16 所示，发现以上岩石的峰值强度和残余强度均满足Hoek-Brown 准则，相关系数在0.85 以上。这表明Hoek-Brown 准则同样适用于描述水-力耦合作用下岩石峰值强度和残余强度的变化规律。结合式 (10)、(12)和图16，获得水-力耦合作用下岩石的Hoek-Brown 准则参数，见表4，并绘制散点图(图17)。由图17 可知，水-力耦合作用下大理岩、中细砂岩、煤和砂岩的ms均大于mr，ms/mr介于1.98～8.66，这是因为岩石在残余阶段时，已经发生剧烈破坏，岩石坚固性和强度大幅下降。