远场应力作用下底抽巷对底板隔水性能影响及加固技术优化

李见波，苗 葳，李振华，韩久方，许海涛，李 鹏

(1.华北科技学院 矿山安全学院,河北 燕郊 065201；2.焦作煤业(集团)有限责任公司,河南 焦作 454000；3.河南理工大学 能源科学与工程学院,河南 焦作 454003；4.焦作煤业(集团)新乡能源有限公司,河南 新乡 453600；5.内蒙古黄陶勒盖煤炭有限责任公司,内蒙古 鄂尔多斯 017000)

石炭二叠系煤层下方岩层中赋存着奥陶系灰岩和不同层数的薄层灰岩。由于这些承压灰岩裂隙含水层，许多矿井需要带压开采，比如河南焦作矿区、河北峰峰矿区、邢台矿区、山东肥城矿区和安徽淮北矿区等，这些矿井都采用了煤层底板注浆加固技术。这些矿区有些高产高效矿井不仅受到煤层底板承压水威胁，还受到煤与瓦斯突出威胁，为解决瓦斯问题，需在底板岩层中布置瓦斯抽采巷道，底抽巷影响底板隔水性能，这极大增加了矿井突水危险性。而在焦作矿区受水灾威胁工作面施工底抽巷是普遍的，不仅给矿区安全生产带来了更大的威胁，还给传统底板注浆加固技术增加难度。为此，笔者拟在传统注浆工程封堵裂隙含水层增加岩层强度基础上研究注浆工程中浆液充填套管的作用，探索底抽巷道条件下浆液封堵裂隙提升岩体强度与浆液充填套管控制浅部底板岩层变形的协同加固机制。

实践中，底抽巷布置一般按照底板破坏区以下而又尽可能远离含水层的原则，对其扰动深部岩层变形再次底板破坏区机制研究较少。针对底板巷道对底板岩层的影响，通常以巷道为中心研究其周边塑性区对底板岩层的影响，而研究巷道轴向效应对岩层变形的影响很少。轴向上巷道破坏了岩层的完整程度而影响底板岩层承力结构，类似蠕变，地应力作用下深部岩层的变形会不断影响上方底板破坏区，如造成滞后性底臌或者突水现象。以传统经典力学为基础，针对底板岩层结构的研究有很多，如文献[1-2]建立了采场底板突水的KS 理论，将采场底板岩层视为岩层薄板，如四边固支、三固支一自由、三固支一简支等。在巷道及围岩变形破坏方面，学者们开展了很多以巷道为中心研究，如以巷道为中心研究巷道围岩地质力学特性、围岩变形破坏特征与机制[3-4]、巷道围岩应力场、位移场和支护方式[5-6]等。针对底板抽采巷道的研究，多以工程应用为主，注重底板抽采巷道位置确定与优化分析[7-8]。在底板突水理论方面成果很多，近年来以传统经典力学理论为基础扩展现场应用，如“下三带”理论[9-10]影响非常大，底板破坏深度一致被使用；文献[11]总结提出了原位张裂与零位破坏理论；文献[12]针对裂隙变形与突水的关系分析研究采动对岩体孔隙-裂隙类型升降变化的影响；文献[13]对底板应力分布、岩体变形及破坏后的渗流等进行研究，

关于巷道围岩和底板岩层变形破坏的研究成果很多；相对而言，以巷道所在岩层为研究对象，开展远场地应力作用下底板破坏区下方巷道轴向效应对岩层变形的影响的研究很少。笔者根据底抽巷的轴向和断面特征，建立远场主地应力作用下底板关键岩层抗弯性能分析模型，求解有底抽巷和无底抽巷时底板破坏区下方关键岩层的变形和弯矩值，进而研究底抽巷条件下注浆加固工程中浆液充填套管对岩层控制作用并进行验证，本研究有益于注浆加固技术的优化，也有利于研究远场应力作用下底臌机制研究。

1 研究区工程概况

1.1 地质条件与巷道布置

1.1.1工程地质与水文地质

研究区煤层底板赋存多层灰岩，其中，直接充水含水层为L8灰岩含水层，平均厚度7.5 m，距煤层底板约21.5 m，中间夹一层0.5 m 左右的L9灰岩；深部灰岩含水层L2水压约2.5 MPa。该矿发生煤与瓦斯突出事故60 余次，最大突出煤量3 000 余 t，突出最大瓦斯量约30 万m3。矿井受到承压水和瓦斯带来的双重威胁，为安全回采，通常在底板岩层中布置底板巷道抽采瓦斯，一般布置在底板破坏带以下又远离含水层的位置。工作面分层开采，平均采高为3.5 m，直接底为炭质泥岩，平均厚约1.0 m，基本底为粉砂岩，平均厚约9.6 m。煤层平均倾角9.5°。底抽巷道布置和底板主要岩层柱状如图1 所示。底抽巷主要揭露第II 层粉砂岩，顶板揭露L9薄灰岩。

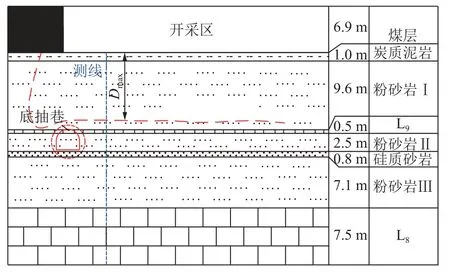
图1 主要岩层与巷道布置示意Fig.1 Schematic diagram of roadway and key floor strata

1.1.2底抽巷与底板破坏区位置确定

底臌是支承压力作用下底板破坏区的直接显现，在深部岩层发生变形后，底板破坏区会不断受到扰动。采动支承压力作用下底板岩层破坏形成底板破坏区[13-14]，支承压力作用下形成的底板破坏深度Dmax为

研究区地面标高约+90 m，工作面标高为-181～-236 m，埋深最大值326 m，平均容重γ取24 kN/m3。底板岩体的内摩擦角的等效值估取37°，煤层内摩擦角估取35°，采高为3.5 m。

将数据代入式(1)，得到底板破坏区最大深度约为11.7 m。第I 层粉砂岩被破坏，第II 层粉砂岩(2.5 m)与第III 层粉砂是抵抗下方传递应力的关键岩层。

1.1.3无支护底抽巷道垂向影响范围

底抽巷影响岩层的高度包括巷道开挖高度，还应该包括周边的塑性破坏区。当底抽巷无支护时周边破坏区范围最大。煤层开采前，底抽巷道周边形成围岩破坏区。为简化流畅，暂按照静水压力水平条件下的圆形洞室的破坏区域计算模型进行分析，巷道周边极限平衡区半径Rjx可按照下式求解：

式中，φ为内摩擦角，巷道周边多岩层时使用等效值；p0为原岩应力；C为岩石黏聚力。

巷道规格为4.0 m×3.0 m，按照圆形巷道理论，半径R0近似取2.5 m，原岩应力按照最大主应力取值为p0=12.4 MPa，岩石黏聚力C=1.5 MPa，巷道围岩的内摩擦角的等效值估取35°，根据式(2)计算得到无支护底抽巷极限平衡区半径Rjx=3.6 m。垂向上，底抽巷切断了整层粉砂岩II，巷道开挖破坏粉砂岩II 横断面如图2 所示。

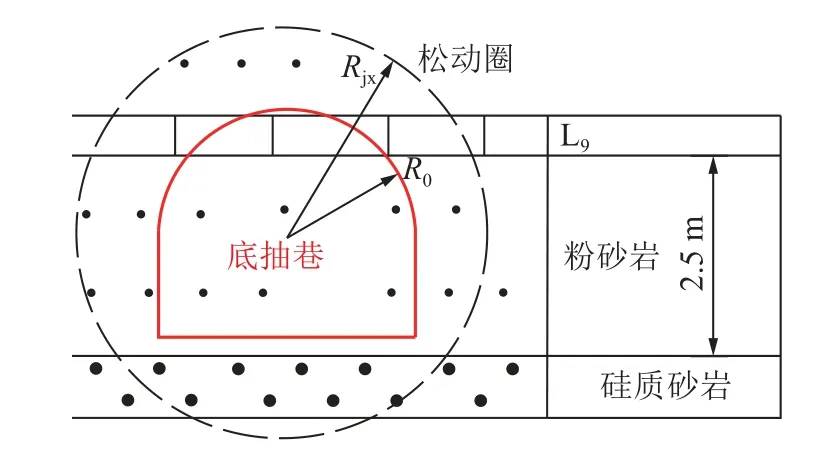
图2 无支护底抽巷道开挖破坏粉砂岩II 断面Fig.2 Section of siltstone II damaged by excavation of unsupported bottom pumping roadway

1.2 底抽巷影响下粉砂岩II 空间受力特征

1.2.1底抽巷对粉砂岩II 边界影响分析

沿巷道轴向上，底抽巷布置如图3 中虚线所示，原来完整的粉砂岩II 被巷道破坏。由于在运输巷和开切眼下方布置底抽巷，第II 层粉砂岩2 个邻边被破坏，沿着巷道轴向相应的力学边界条件由固支变为自由边界。煤层开采底板破坏区形成后，粉砂岩II 和III 是抵抗应力的关键岩层，而底抽巷使粉砂岩II 的抵抗变形能力降低。

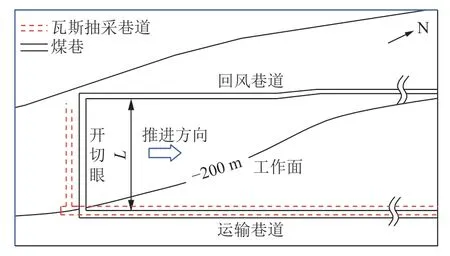
图3 底抽巷布置及对粉砂岩II 的影响Fig.3 Roadway layout and its influence on siltstone II

1.2.2远场应力作用下粉砂岩II 受力分析

地应力场是影响煤层底板岩层变形的主要因素，其中，地应力σ2和σ3为研究区受到的主要原始主应力。开采卸压后，上方应力解除，导致底板岩体应力状态由三向变为两向或单向状态，局部应力场被打断，但是在煤层底板一定深度区域仍属于原始应力场环境，应力从下向上逐点传递。开采卸压后粉砂岩II 上部的底板破坏区以自重力为主，影响有限暂忽略。

在远场地应力作用下，粉砂岩主要承受深部远场应力传递而来的应力σ′。根据文献[15]地应力测试结果，确定研究区域的原始主应力σ2和σ3分布如图4 所示。开采卸压后底板深部远场主应力向上传递，底板岩层受到力的作用会发生变形。

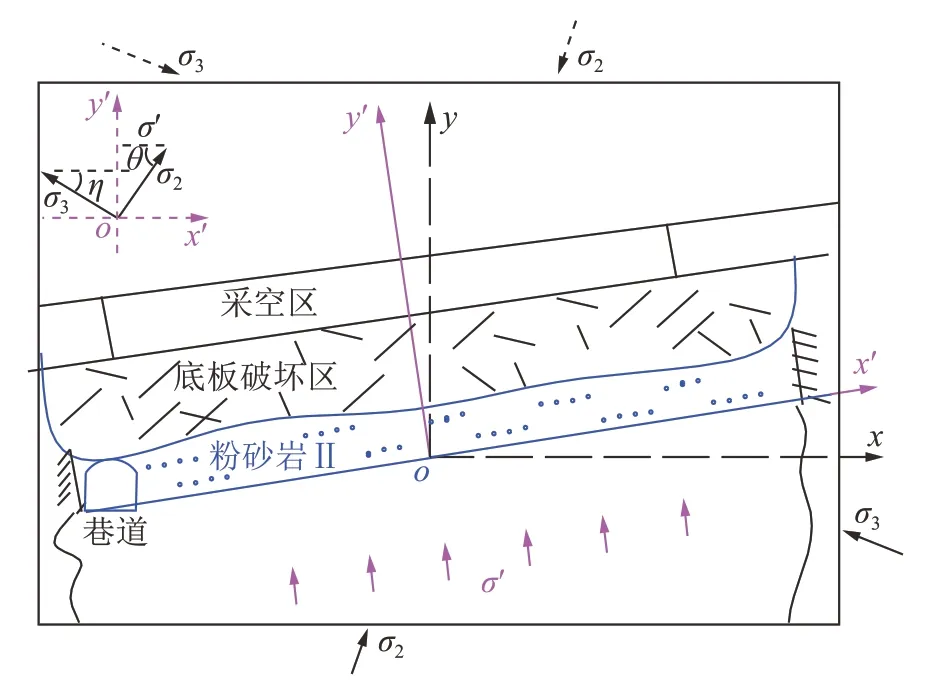
图4 开采卸压后远场应力作用下底板粉砂岩II 受力状态Fig.4 Stress state of floor siltstone II under far-field stresses after pressure relief caused by mining

在局部坐标系x′oy′中，远场主应力作用下粉砂岩II 受到应力分量σ′作用，经换算可得该应力分量σ′的取值为

式中，S为应力传递衰减系数，取值[0,1]，远场原岩应力区S取1；θ为σ2与水平面的夹角；η为σ3与水平面的夹角。

据此，参考地应力实测值，得到该区域粉砂岩承受的应力分量为σ′=8.1SMPa。

2 远场应力作用下底抽巷对粉砂岩II 力学性能影响分析

2.1 底抽巷影响下粉砂岩II 变形力学模型

根据弹性薄板理论，若板的厚度远小于板的中间平面的最小尺寸，这个板可称为薄板。底板破坏区下方粉砂岩符合薄板情形[1,16]。根据图2、3 的几何边界条件，建立底抽巷影响下粉砂岩II 薄板力学模型，如图5 所示。设薄板岩层长为a，与工作面长度对应，宽为b，与工作面推进距离对应，M表示边界处弯矩。

图5 粉砂岩II 变形力学模型Fig.5 Mechanical model of siltstone II deformation

空间上，煤层开采后局部卸压区形成，远场应力作用下这层砂岩会发生变形或有变形趋势。在采空区下方以底抽巷为两邻边的砂岩平面上，受到扰动部分和未开始变形部分之间会存在一个变形分界面(虚线)，由于变形分界面属于完整砂岩，具有固定端作用，近似视为固定边约束，将该变形分界面作为砂岩薄板的另两邻边。

2.2 两邻边自由条件粉砂岩II 的变形与弯矩

根据图5 粉砂岩II 的薄板模型，底板巷道使得粉砂岩II 边界变为两邻边自由和两邻边固定边界。为方便，粉砂岩II 承受的远场应力分量暂视为均布载荷。薄板上方压剪破坏区岩体破碎，以重力作用为主，暂忽略。考虑工作面推采距离对变形的影响，分别求解工作面推进不同距离时(推进距离与工作面长度比分别为0.50、0.75、1.00、1.50 和1.75)，在传递远场应力分量作用下底板岩层变形和弯矩值。

根据广义简支边理论[17-18]，两邻边自由和两邻边固定的边界条件如下：

两邻边自由固支薄板的挠曲面一般采用叠加法进行理论计算。两邻边固支两邻边自由的底板岩层可分解为4 种类型，5 个无穷联立方程和5 个未知量。

(1)均布荷载q作用下的简支边矩形板。其边界各为x=0，x=a，y=0，y=b，a为沿x方向固定边长度，b为沿y方向固定边长度。先求得板的挠曲面，然后求得剪力(Vx)x=a、(Vy)y=b，斜度(∂W/∂x)x=0=(∂W/∂y)y=0=0和角点的集中力(R)x=a,y=b。

(4)因为自由角点M有位移，假设弯曲面W=kxy，其中k为待定系数。则求得角点的集中力(R)x=a,y=b=2D(1-μ)k；沿x=0 和y=0 两边的斜度分别为(∂W/∂x)x=0=(∂W/∂y)y=0=0。

(5)叠加条件。各部分叠加后需要满足以下条件：①固定边x=0 和y=0 的斜度为0，即(∂W/∂x)x=0=(∂W/∂y)y=0=0；②沿自由边x=a和y=b的剪力为0，即(Vx)x=a=(Vy)y=b=0；③作用于角M点的集中力为0，即(R)x=a，x=b=0。各部分的结果进行叠加，在局部坐标系中，得到5 个无穷联立方程，包含am、Em、bi、Fi和k共5 个未知量，m、i取值为1,2,…,50。

其中，αm=mπb/a，βi=iπa/b，m/i=1，2，3，……，但是与q有关的项m/i=1，3，5，……。

(6)理论解答。在局部坐标系中，设沿x方向固定边长度为a，沿y方向固定边长度为b，μ取0.3。因为am收敛快，而Em收敛慢，各个系数计算时取50 项。无穷方程的矩阵形式为[C][am,E,bi,F]T=[q]，其中[C]为系数矩阵。所以，可得到未知量矩阵 [am,E,bi,F]T=[C]-1[q]。

(7)底抽巷影响下粉砂岩II 变形理论分析。工作面开采不同距离时巷道影响下底板岩层变形如图6所示。为阐明底抽巷道对粉砂岩II 变形的影响，比较分析有底抽巷道和无底抽巷时粉砂岩II 的变形机制。工作面推进距离与工作面长度比分别为0.50、0.75、1.00、1.50 和2.00 时，有底抽巷和无底抽巷2 种情况，粉砂岩II 最大变形理论解见表1。

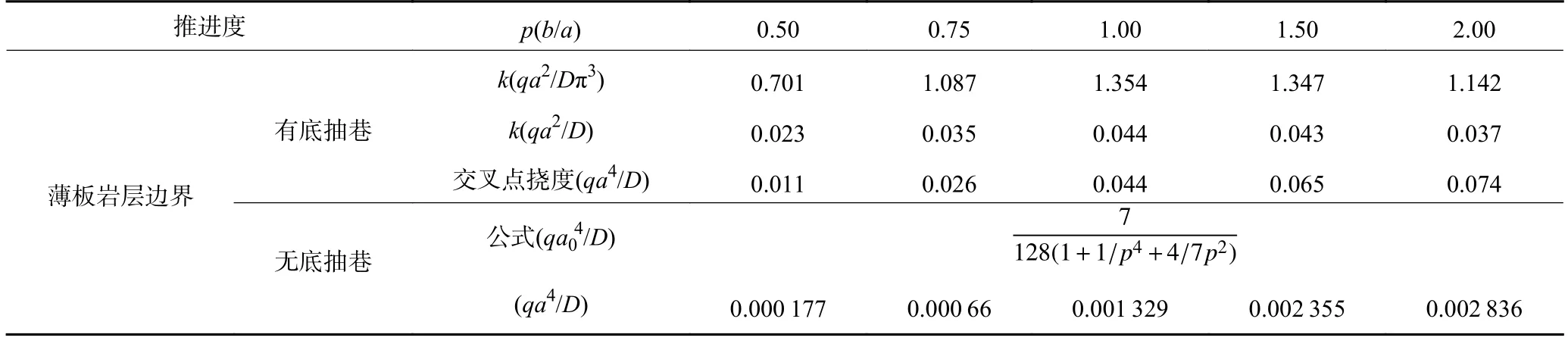
表1 不同推进距离底板岩层薄板变形理论解Table 1 Theoretical solution of thin plate deformation of floor strata with different advancing distance

图6 工作面开采不同距离时巷道影响下底板岩层变形Fig.6 Floor rock deformation under the influence of roadway with different mining distances

为便于比较，将四边固支条件下不同推采距离时薄板岩层中心点最大挠度列出，见表1。对于相同形状和尺寸的薄板岩层，边界条件不同，薄板的最大变形及变形位置不同。有底抽巷时薄板岩层最大变形发生在自由角点处，且远大于无底抽巷条件下的薄板岩层最大变形值(图6(f))。由表1 中的理论解可知，有底抽巷与无底抽巷时的最大变形值相比，2 者相差1～2 个数量级。理想弹性条件下，随着推进距离与工作面长度之比增加，薄板岩层自由角点出的变形不断增加；如当b=2a时，薄板岩层角点的最大变形为0.074(qa4/D)，远大于四边固支薄板岩层变形值。

目前深部二灰含水层是主要威胁，水压较高，埋藏较深。地应力是在天然原始状态下测得，暂将深部远场中水压力作为总地应力的一部分一起向上传递。初次来压前，底板岩体单向受力特征明显。初压步距一般小于50 m，当工作面推进距离50 m 时，远场应力衰减系数S取0.185，粉砂岩II 弹性模量40 GPa，粉砂岩II 厚度为2.5 m，巷道影响岩层厚度按7.0 m，泊松比取0.3。将数据代入表1 中的理论公式，计算得有底抽巷道时岩层最大变形值为1.31 m，无底抽巷时粉砂岩II 的最大变形值为0.02 m。底抽巷道影响下，粉砂岩II 最大变形值明显大于无巷道影响四边固支条件时岩层最大变形值。

(8)有无底抽巷时粉砂岩承受最大弯矩。边界条件的改变对粉砂岩周边承受弯矩造成很大影响，承受最大弯矩值明显提高。与变形分析相对应，分析了不同推采距离时未破坏边的弯矩值，并与四边固支条件进行比较。计算得到3 种不同推采距离条件下固定边弯矩如图7 所示。

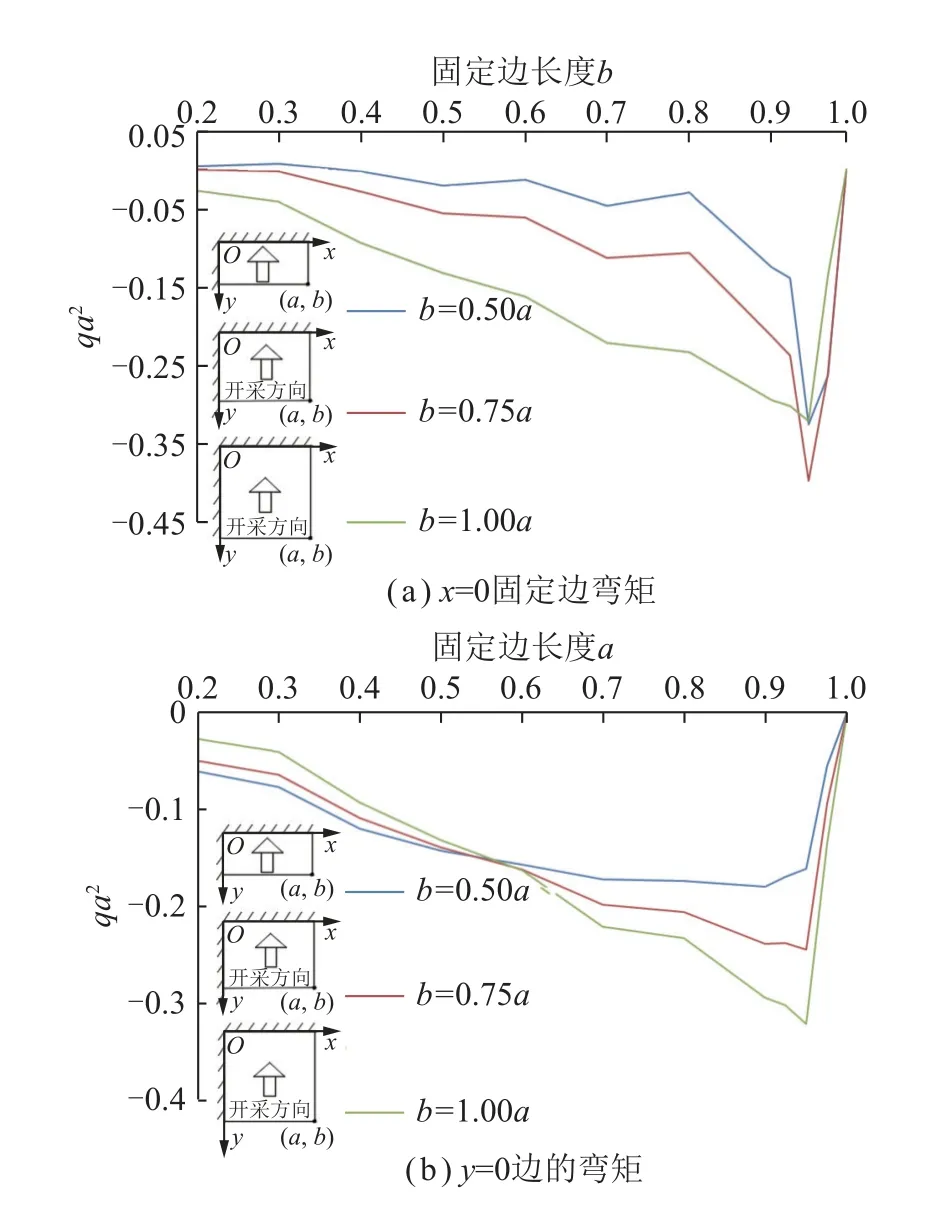
图7 3 种形状的薄板岩层固定边上的弯矩分布Fig.7 Bending moment distribution on the fixed edge of thin plate rock strata with different shapes

3 种开采距离相比较，最大弯矩发生在b=0.75a条件下x=0 边的y=0.975b处，此时弯矩为0.397 69qa2。为说明底抽巷道对粉砂岩抗弯强度的影响，计算得到了上述3 种情形四边固支条件下的最大弯矩值。对于四边固支薄板，弯矩的绝对值最大发生在长边的中心部位。最大主弯矩[14]按照式(9)计算：

式中，λ1=b/a，μ为泊松比，与上文一致取0.3。

经计算，四边固支边界条件下，3 种情形(b=0.5a、b=0.75a和b=1.0a)对应最大主弯矩值分别为：0.019 181qa2、0.037 872qa2和0.049 292qa2。

2 种不同边界条件下，模型固支边承受的最大弯矩相差1 个数量级。底抽巷影响下，粉砂岩承受的最大弯矩明显增大，与变形分析结果一致，进一步阐明了通过增加约束改善粉砂岩边界条件的必要性。

3 底抽巷条件下底板注浆加固技术优化与数值验证

3.1 加固工程

为确保工作面运输底抽巷掘进安全，避免水害事故发生，对巷道掘进区域进行超前预注浆加固施工。底板注浆加固工程布置如图8 所示。施工的钻孔开孔均为φ150 mm 孔径，终孔均为φ75 mm 孔径，下两级套管，一级套管直径为φ146 mm，二级套管直径为φ108 mm。一级套管下至过煤层底板0.5～1.0 m；二级套管下至距L9灰岩底面下法向距离5.0 m。累计钻探进尺24 000 余米，其中一级套管总长度3 000 余米，二级套管总长度6 000 余米，注入干料17 797.11 t，其中水泥2 500 余吨，工程量巨大，成本高。

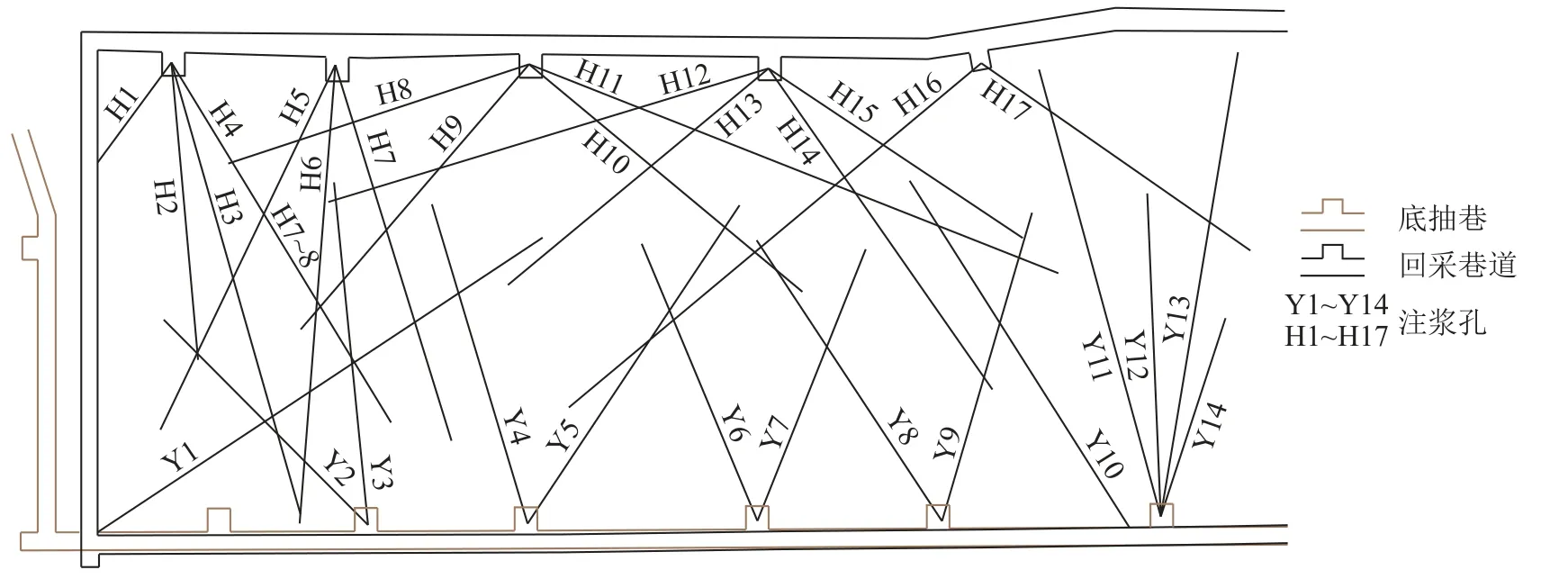
图8 工作面底板注浆工程部分套管布置示意Fig.8 Layout of grouting engineering in the working face floor strata

3.2 注浆加固中浆液充填套管作用机制与工程效果可行性分析

传统注浆加固的主要作用是浆液封堵裂隙，消除突水通道的同时增加了岩层的强度，注浆套管作为注浆工具，用来辅助注浆和及时封堵钻孔施工中的出水。实践中，注浆完成后，高压封孔，套管被浆液充满，凝固浆液和套管成为底板岩体的组成部分。当加固深度较大、含水层水压高时，需要施加多级套管，套管长度加大，上述底板注浆加固工程中一级和二级套管累计9 000 余米。浆液充填套管类似混凝土钢管和微型桩等结构，凝固浆液和套管成为底板岩体的组成部分，增强了岩体的性能。在注浆封堵深部裂隙含水层改善岩体强度基础上[19]，根据围岩与浆液充填套管作用力与反作用力的原理，研究大量浆液充填套管在煤层底板注浆加固中控制浅部底板岩层变形与破坏的积极作用，井下注浆封堵裂隙含水层及控制煤层底板岩层变形双重作用如图9 所示。

图9 井下注浆封堵裂隙含水层及控制煤层底板岩层变形双重作用示意Fig.9 Sketch map of double functions of underground grouting to seal fissured aquifers and control the deformation of floor strata

在加固技术优化方面，笔者主要研究底抽巷道条件下注浆加固工程中浆液充填套管的作用与可行性。底板注浆加固工程中浆液充填套管具有很好的抗弯性能，文献[20-23]在分析底板空间应力状态的基础上，阐明了煤层底板注浆加固中浆液充填套管的作用机制，通过合理布置浆液充填套管能够控制底板变形。其中，稳定岩层提供浆液充填套管作用的固定端，如图10(a)所示。以准滑动面为界，下段变形较小套管视为固定端，上段变形较大套管视为自由端，套管抗弯变形主要由套管上正应力σN引起。据此，注浆工程中设计浆液充填套管布置和作用机理如图10(b)所示。浆液充填套管加固到L9灰岩下垂距5 m，进入粉砂岩III 垂直距离2 m，属于稳定的固定端，起到很好的锚固作用，套管能够发挥套管的抗弯性能，在抗弯强度范围内，能够抵抗岩体变形，多个套管组合效果更好。由于套管的锚固作用，改善了粉砂岩II 的边界条件，增加了约束，加固理想状态时达到四边固支条件。

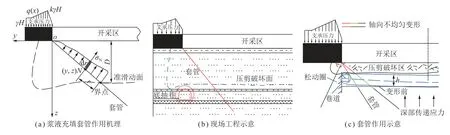
图10 浆液充填套管作用机制与工程布置示意Fig.10 Mechanism of slurry filling casing and its engineering layout

注浆工程中组合套管布置及巷道影响下套管在岩层中的作用如图10(c)所示。套管布置方式的不同，在岩层中的位置不同，套管的轴向变形有所不同。布置在巷道影响岩层中的套管在轴向上的变形呈现三段式，未受巷道影响的套管轴向变形呈现两段式。

3.3 加固效果数值验证

(1)边界条件与初始条件。套管与围岩是一对作用力与反作用力的关系，通过跟踪套管的变形情况可以得到底板加固区域围岩控制效果。根据现场地质条件建立三维数值模型，数值模型边界条件施加需要考虑远场原岩主应力方向，在远场主应力作用下，数值模型边界需要施加正应力σc′、σc″和切应力τ。根据地应力场的实测结果[15]，数值模型应力边界条件如图11 所示。

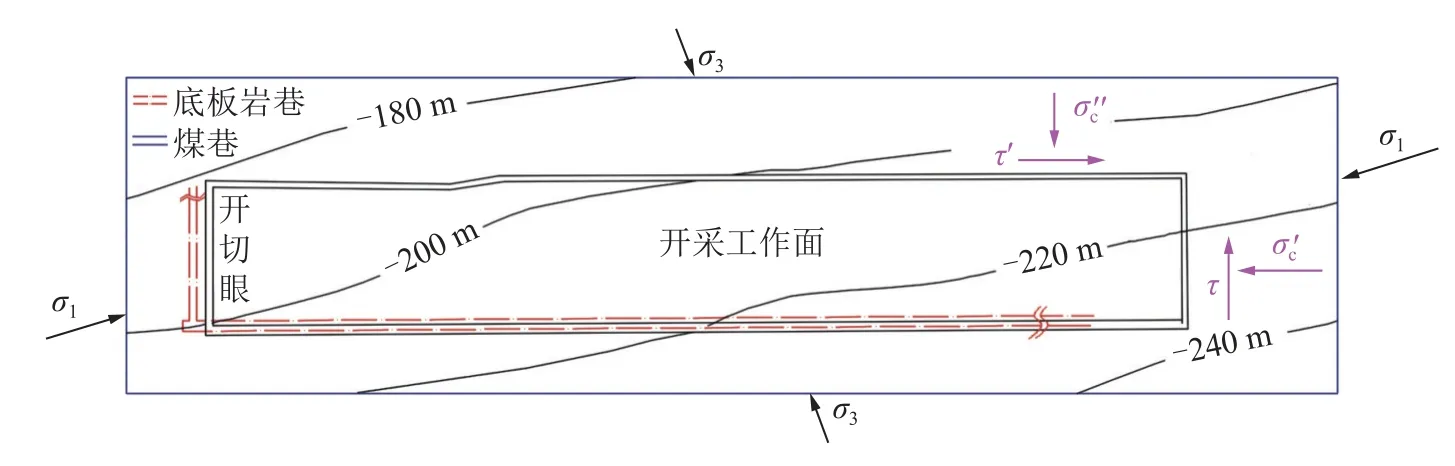
图11 研究区域应力边界示意Fig.11 Schematic diagram of stress boundary conditions in the studied area

研究区域外边界主要受到远场原始主应力σ1和σ3作用，设以开采方向为法线的斜截面的外法线n与主应力方向夹角为α，则该斜截面上的正应力σn和切应力τ分别为

地应力σH最大14.1 MPa，最小为5.1 MPa。工作面开采方向为法线的斜截面的外法线n与主应力方向夹角为α取15°。计算得到σn=13.49 MPa；τ=2.25 MPa。

模型中设4 个钻场，沿着巷道方向钻场间距100 m，每个钻场按照设计布置7 个钻孔，并列布置，采空区外侧加固套管暂未考虑，如图12(a)所示。简化套管级数，计算中选用直径108 mm 的无缝套管。

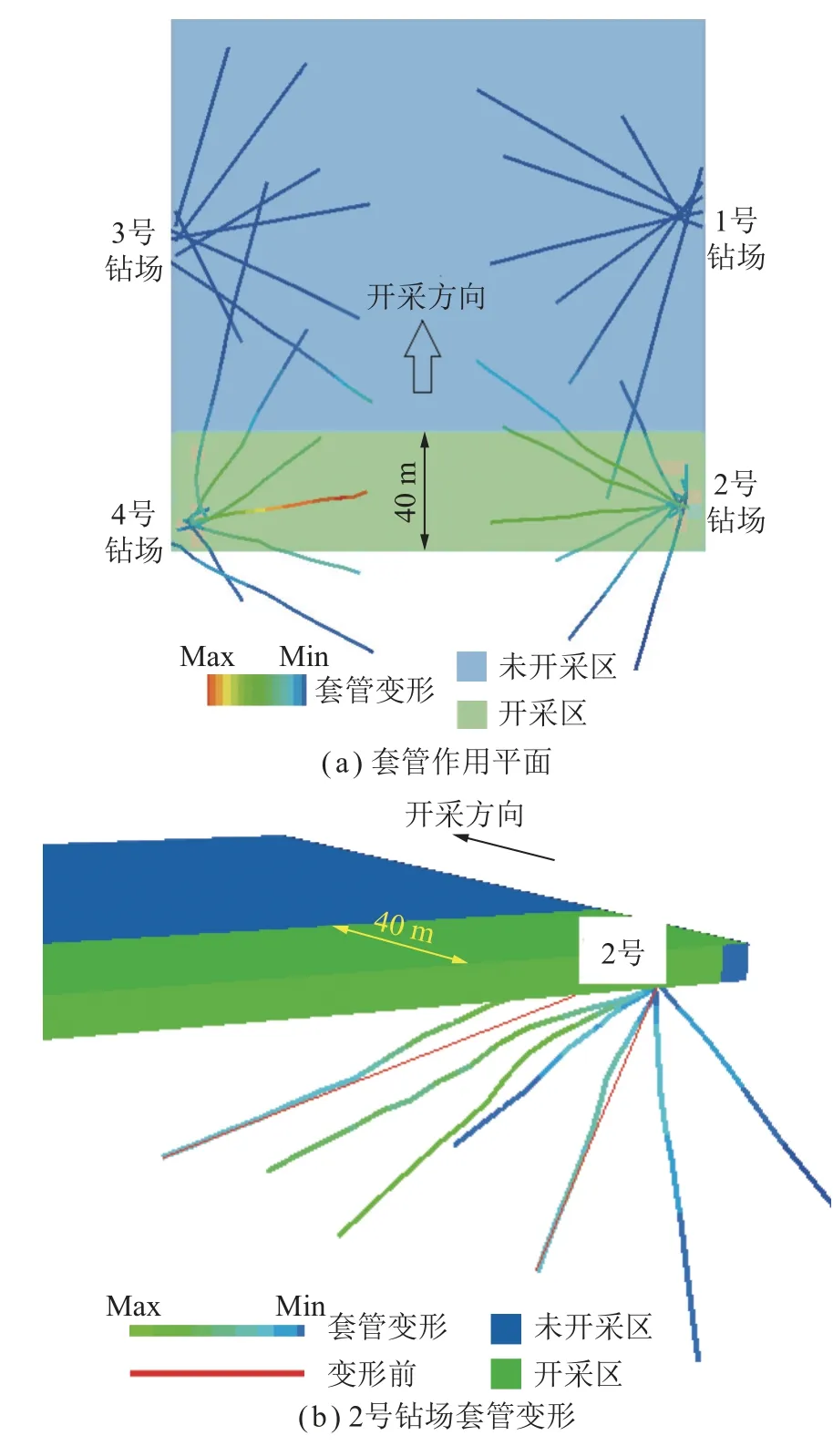
图12 工作面开采40 m 时组合套管变形数值计算结果Fig.12 Deformation of the combined casing pipes got by numerical calculation with mining distance of 40 m

(2)套管与围岩变形分析。以钻场2 号为例，为展示清楚套管作用机制，图12(b)中只显示采空区和未开采区煤层图例，其余岩层未显示。套管布置位置不同，套管的变形不同。有两段式有三段式。与变形前轴线相比，变形量明显，根据作用力与反作用力，套管发挥了抵抗岩层变形的作用。通过数值计算很容易得到多个组合套管作用效果。当遇到长巷道切割岩层时，浆液充填套管组合的锚固作用能够增加薄板岩层边界约束，减少自由边界，提高岩层的整体抗弯性能。理想加固时可将岩层的自由边界转换为固支边界，使得底板岩层的薄板结构更加稳固，提高岩体的完整性，防止工作面回采过程中发生底鼓引起深部强含水层导出发生大的突水事故。

数值计算得到了无底抽巷、有底抽巷加固和不加固3 种条件下的岩层变形值，监测结果如图13 所示。首先在各个岩层中共布置测点形成测线，测线布置如图1 所示。无底抽巷时位移值整体小于有底抽巷道时位移值。3 种条件下数值计算得到最大位移值分别为0.28、0.40 和0.42 m。无底抽巷到时位移变化更加连续。而巷道影响下位移曲线有分段特征。

图13 3 种条件下测线上各监测点垂向位移曲线Fig.13 Vertical displacement curves of monitoring points under three different conditions

生产实践中，该矿区底臌最大变形2.5 m 以上，针对底抽巷道的治理，在破碎区不仅仅采用长套管注浆，而且进行全断面充填，最大限度增加约束条件，这样能够很好地控制底板岩层变形，起到防治底臌大变形和突水的效果。注浆套管可能无法将简支边界改变为像原有完整岩层一样的固支边界，当很多浆液充填套管共同作用时通过增加约束有效抵抗岩层变形，一定程度上起到锚固岩层作用。通过对底板加固岩层进行超前长套管注浆加固，有效减少回采期间巷道底臌变形，底抽巷掘进过程中没有发生突水事故，矿井正常生产有保障，大大增加矿井经济效益。底板注浆加固工程中浆液充填长套管的组合抗弯刚度能够起到阻抗薄板岩层变形的控制效果，与浆液封堵含水层功能组合使用，既阻隔突水通道又控制岩层变形，两者组合使用时能够有效改善底板岩层控制效果，研究井下注浆封堵深部裂隙含水层及控制浅部煤层底板变形协同作用有利于优化注浆加固技术和底板岩层控制技术。

4 结论

(1)地应力场是影响煤层底板岩层变形的主要因素，根据研究区主要远场主应力σ2和σ3赋存条件得到局部坐标系x′oy′中作用在粉砂岩II 的应力分量为σ′；然后基于底抽巷的轴向和断面特征，建立远场主应力作用下底板关键岩层抗弯性能分析模型。计算得到采动支承压力作用下工作面底板岩体压剪破坏范围和底抽巷道周边松动圈，并根据工作面底板岩层柱状图，确定粉砂岩II 和III 是抵抗水压力的关键岩层，底抽巷道破坏粉砂岩II 的力学边界条件，使粉砂岩II由四边固支转变为两邻边自由两邻边固定边界。

(2)运用广义简支边和叠加法得到采空区下方粉砂岩II 变形和弯矩理论解，得到工作面推采距离与工作面长度比分别为0.50、0.75、1.00、1.50 和2.00 时粉砂岩II 在巷道边界处的变形值，近似弹性条件下粉砂岩II 在底抽巷交叉点处的位移最大，且大于四边固支条件下同尺寸岩层最大位移；底抽巷影响下粉砂岩II固定边承受的最大弯矩值比固支边时高一个数量级。同等条件下底抽巷影响使粉砂岩II 更易发生变形，降低粉砂岩II 抵抗变形能力。

(3)底板注浆加固工程中将浆液充填套管进入粉砂岩III 垂直深度2 m，该段套管可作为其发挥抗弯作用固支端，给粉砂岩II 自由边增加约束，注浆加固工程中浆液充填长套管在加固范围内由于抗弯性能等增加约束，改善粉砂岩II 边界条件起到增加抵抗强度的效果。数值计算结果验证了底抽巷道条件下注浆加固工程中浆液充填套管对粉砂岩II 变形的实际效果。本研究可为类似矿井的底板注浆加固技术和底板大变形控制技术提供理论支持。