基于PVC-CAE的轴承剩余寿命预测方法
2023-10-17张远亮李海浪
张远亮 李海浪


摘 要:轴承由于在制造、安装以及工况上的不同,退化过程有很大差异,在轴承的剩余使用寿命预测中,特征的轴承个体差异会直接影响到后续模型的训练难度和预测精度。为了在提取特征时减小轴承的个体差异性,提出了一种并行方差约束卷积自编码(parallel variance constrained convolutional auto-encode,PVC-CAE)的轴承退化特征提取模型。具体方法是在卷积自编码的框架内定义并行方差约束,通过改进卷积自编码的损失函数,搭建出PVC-CAE模型。PVC-CAE模型可以有效地降低同标签特征的轴承个体差异性,提升预测精度。预测流程为:先用PVC-CAE模型在频域信号内提取特征,再用LSTM网络预测。通过PRONOSTIA实验平台所获取的实验数据集以及西安交大轴承数据集对所提方法进行了验证,同时与另外三种方法进行对比,实验结果表明,所提方法在轴承剩余使用寿命预测中取得了较好的结果,并且在不同的工况下具有一定的泛化性。
关键词:寿命预测;轴承;特征提取;个体差异性;方差约束
中图分类号:TH17 文献标志码:A 文章编号:1001-3695(2023)10-029-3070-06
doi:10.19734/j.issn.1001-3695.2023.02.0067
Remaining life prediction method of bearing based on PVC-CAE
Zhang Yuanliang1,Li Hailang2
(1.College of Intelligent Manufacturing & Transportation,Urban Vocational College of Sichuan,Chengdu 610110,China;2.School of Mechanical Engineering,Southwest Jiaotong University,Chengdu 610031,China)
Abstract:Due to the different manufacturing,installation and working conditions of bearings,the degradation process is very different.In the prediction of the remaining service life of bearings,individual bearing differences of characteristics will directly affect the training difficulty and prediction accuracy of subsequent models.In order to reduce the individual differences of bea-rings during feature extraction,
this paper proposed a PVC-CAE model for bearing degradation feature extraction.The specific method defined the parallel variance constraint within the framework of convolution self-coding,and built the PVC-CAE model by improving the loss function of convolution self-coding.The PVC-CAE model could effectively reduce the individual bearing differences of the same tag characteristics and improved the prediction accuracy.The prediction process is as follows:firstly,the PVC-CAE model was used to extract the features in the frequency domain signal,and then the LSTM network was used to predict.The proposed method was verified by the experimental data set obtained from PRONOSTIA test platform and the bearing data set of Xian Jiaotong University,and compared with the other three methods.The experimental results show that the me-thod achieves good results in the prediction of the remaining service life of bearings,and has certain generalization under diffe-rent working conditions.
Key words:life prediction;bearing;feature extraction;individual differences;variance constraints
0 引言
近年來,随着故障监测和维修技术的快速发展,故障预测与健康管理(prognostics and health management,PHM)已经成为重要的研究方向[1]。轴承是机械系统中使用最广泛的元件之一,轴承的运行状态直接影响到整个机械系统的正常使用。在实际的工业应用中,仅仅判别轴承是否发生故障以及识别故障类型是远远不够的,不能满足工业生产的实际需求。对轴承进行剩余寿命预测能预知轴承的损伤,有利于提升整个机械系统运行的可靠性,避免严重的故障,减小维修成本[2]。因此,及时了解轴承的退化状态并预测轴承的剩余寿命,对于机械设备的运维具有重要的工程意义。
轴承的剩余使用寿命预测方法大致可以分为基于模型的方法和基于数据驱动的方法[3]两大类。工业大数据与人工智能技術的兴起,使得基于数据驱动的轴承寿命预测方法的应用越来越广泛,逐渐成为主流[4,5]。基于数据驱动的轴承剩余使用寿命包括三个阶段:a)从有噪声的信号中提取特征;b)建立预测模型;c)利用第二阶段的预训练模型进行预测[6]。提取特征是基于数据驱动方法中的关键一环,能否提取好的退化特征直接关系到能否准确预测剩余寿命。
目前,国内外学者在提取轴承退化敏感特征上作了大量的研究工作,但是提取特征时对轴承的个体差异性考虑较少。受制作材质、工艺流程以及工况等因素影响,不同轴承的退化过程是多样的,所提取的退化特征也具有个体差异性。即使是同一批次、同一型号的轴承在相同的工况下工作,由于其本身具有的不确定性、非线性、时变性的特点,退化过程仍然是有差异的,尤其是不同轴承的失效形式不一样,个体差异在退化末期更加显著。除此之外,轴承退化个体差异性也体现在各轴承全寿命区间分布的离散性上。轴承的全寿命区间是指轴承从正常状态经历不同程度的退化状态直至最终失效的渐进演化过程,以PHM2012挑战赛轴承公开数据集为例,其中运行时间最长的轴承运行了467 min,运行时间最短的仅12 min[7]。现阶段轴承的剩余寿命常常用百分比来表示,而百分比标签又由已服役的寿命值与总寿命值计算得到。如此一来,在提取训练集轴承特征时容易面临这样一个情况:由于存在轴承退化的个体差异以及寿命区间分布的差异,同一剩余寿命标签会对应多个不同的样本特征,即不同的训练轴承中,剩余使用寿命标签一致,但它们对应的样本特征不一致。这种同标签特征的轴承个体差异性增加了后续预测模型的训练难度,继而影响到预测结果。针对这个问题,现在已经有一些学者开始关注,例如文献[8,9]通过提取相对特征,降低训练集轴承之间的差异,从而提升了预测方法的适用性与稳定性。在对轴承寿命预测的特征评价研究工作中,Li等人[10]提出了基于趋势相似性的评价指标对特征进行筛选,选出的特征在不同的训练集轴承上具有相同的趋势,实则是为了使得各轴承在同标签时的特征具有一致性,此类特征更有利于轴承的剩余寿命预测。康守强等人[11]直接提出在进行可靠度预测的同时也要考虑轴承的个体差异。
综上所述,为了在提取特征时降低轴承退化特征的个体差异性,促进特征的一致性约束,本文提出一种基于PVC-CAE的轴承寿命预测方法。在卷积自编码学习框架内定义并行方差约束,并通过改进卷积自编码的损失函数,搭建了PVC-CAE模型。用PVC-CAE模型提取特征,有利于减小同标签特征的轴承个体差异,从而更好地提取轴承退化特征,提升寿命预测精度。
1 并行方差约束卷积自编码
1.1 卷积自编码
卷积自编码(convolutional auto-encoder,CAE)综合了自编码和卷积神经网络的共同特点,具有局部感知和参数共享两个优势。卷积自编码是一种无监督学习方式,克服了传统人工提取特征—人工选择的缺陷,可以自适应地提取特征,目前在轴承剩余使用寿命预测上取得了众多进展[12,13]。卷积自编码包含编码器和解码器两部分,其中编码器由输入层和中间隐藏层组成,解码器由中间隐藏层和输出层组成。提取训练轴承特征时,通过对重构损失进行优化迭代,更新网络权值,学习一个恒等函数,从而使得所提取的特征尽可能地保留原有数据的大部分信息。卷积自编码的结构如图1所示。
1.2 数据预处理
轴承的振动信号中包含了许多有效的退化信息,分析振动信号来对轴承的运行状态进行监测是目前最主要的手段。然而通过传感器所采集的时域振动数据通常包含大量噪声,直接对原始时域信号进行处理难以得到理想的特征。频域信号内,频带是按照频率从低到高进行排列的,比时域信号的分布更有规律,可以有效降低卷积自编码网络重构信号的难度,所以比时域信号更适合作为输入[14]。因此,本文使用快速傅里叶变换,实现轴承振动数据时域到频域的转变,并将每个训练轴承的数据按照采样顺序分别整理成(m×n)的数组,其中m表示采集总次数,n表示对应时刻的特征量,即每一行代表一条样本数据,每一列代表一维特征。
轴承的寿命标签采用百分比标签yi,其值为1~0,yi计算方法如式(1)所示。百分比标签实质上是对剩余寿命标签做了归一化处理,弱化各轴承全寿命分布离散性的影响,降低训练预测模型时的拟合优化难度,提高剩余使用寿命的预测精度[14]。在应用时,可根据已服役的寿命值与当前预测的百分比标签还原出以时间为单位的剩余寿命值。
其中:j代表该行对应的行序号;m代表总行数。
训练神经网络时,为了提升模型的鲁棒性,通常是将数据打乱,保证训练数据无序,再按照一定批量大小(batchsize)输入到网络中。在PVC-CAE模型中构建并行方差约束时,目的是度量轴承退化的个体差异性,故而每批次都必须将所有轴承的数据共同输入,然而受批量大小的限制,只能对轴承的全寿命区间进行分割,再将每个轴承同标签区间的数据并行依次输入。具体操作是将每个轴承数据按照各自采样总次数mi分割为x等份,即把一个(mi×n)的数组分割为x个(int(mi/x)×n)的数组,int(·)表示取整函数。x取值可根据预设批量大小和训练集轴承数量大小确定,本文以x=50举例说明。将各训练集轴承相同寿命标签区间的数据整合,便是PVC-CAE网络每批次的输入数据,其样本总数目为实际的batchsize,计算方法如式(2)所示。具体操作如图2所示。
其中:h代表训练集轴承总数;mi代表轴承所对应的采样次总数;x代表均分数目;int(·)代表取整函数。
1.3 并行方差约束
原始振动信号经过数据预处理,按照计算所得的batchsize输入到特征提取模型中,以此保证每批次数据都是各训练轴承同寿命标签区间。在卷积自编码具体的训练流程如下所示。在卷积自编码的重构损失中加入并行方差约束,在提取特征时,通过最小化带有并行方差约束项的损失函数来减小同标签特征的轴承个体差异。
经过CAE编码后得到隐层特征,由于不同轴承之间的寿命分布具有很大的离散特性,这导致了不同轴承同一寿命标签区间的样本数量mi/x有很大差异,无法对x个非同型的数组作差异性分析,所以需要采用一定的方法将每个数组压缩至同型数组。在不改变特征整体变化规律的前提下,对每个轴承的隐藏特征按照列为单位分别进行降采样[15]。如图3左图所示,特征A具有长度a1,通过降采样等处理,在不改变特征整体趋势的前提下,将特征A长度从a1压缩至a2;右图p表示隐藏特征的特征长度,m和q分别表示降采样前后的样本数量。
对隐层特征作降采样时,设第i个训练轴承的第r列特征序列为Xri=(Xri(t1),Xri(t2),…,Xri(tm)),经过降采样后变成Zri=(Zri(t1),Zri(t2),…,Zri(tq))。对列进行降采样处理的主要计算公式如下:
其中:m表示降采样前隐藏特征的样本数量;q表示降采样后隐藏特征的样本数量,即把Xri的长度均分成q个区间,取整;k表示每个区间的长度,不取整;roundup(·)表示向上取整函数;L(f)表示第f个区间的长度;Zri(f)表示第f个区间降采样后特征的取值。
提取特征时,同时将h个轴承同标签的数据输入到卷积自编码中,经过编码后,把隐藏特征分别降采样整理成h个(p×q)的数组。计算这h个数组同一位置数据之间的方差,将所有位置的方差进行求和作为并行方差约束。假设第i个轴承(j,k)位置的特征为Xi(j,k),Var(·)表示求方差函数,Var{Xi(j,k)|((i∈N)&(i≤h))}表示矩阵(j,k)位置数据的方差,并行方差约束LV则可表达为
PVC-CAE网络提取训练轴承特征时,PVC-CAE网络的主要损失函数是原始数据的重构损失,使所提取的隐层特征尽可能地保留原有数据的大部分信息。在PVC-CAE网络的重构损失中加入并行方差约束,在提取特征时,通过优化并行方差约束项的损失函数来降低同标签特征的轴承个体差异性。而PVC-CAE网络的重构损失越小,表明隐层特征越能表征原数据;并行方差约束项值越小,表明同标签特征的轴承个体差异性越小。PVC-CAE网络最终目的是最小化重构损失,同时最小化并行方差约束项,即两者是同向优化。在并行方差约束项前增添一个惩罚系数,惩罚系数用以并行方差约束项的损失函数与重构损失之间的权重,那么PVC-CAE模型的损失函数可以表达为式(7),PVC-CAE模型原理如图4所示。
其中:X表示原始数据;表示重构数据;ζ(X,)为重构误差。本文用均方误差(MSE)进行计算。
PVC-CAE的目标函数是一个反复迭代优化的优化问题,训练网络具体的流程如下所示。
2 预测流程
本文先对时域信号作快速傅里叶变换,将其转换为频域信号,再使用PVC-CAE模型进行特征自适应提取。鉴于多层深度学习网络能够提取浅层网络学习不到的特征,PVC-CAE设置了三层卷积和反卷积,用来增强模型的特征提取能力。本文PVC-CAE特征提取模型如图5所示。
轴承剩余寿命预测很明显的一个特点就是时间相关性,即样本数据之间并非是独立的,而是具有很强的时间关联度。LSTM是在循环神经网络基础上进行改进的一种特殊网络,能够捕捉到隐藏在信号里的时序信息,能更精确地预测轴承剩余寿命,因此本文将LSTM网络作为预测模型。构建LSTM神经网络预测模型时,由于多层LSTM网络能更充分地利用具有时间相关性的退化历史数据提取轴承退化时序特征[16],所以LSTM预测模型采用的是四层网络,并通过一个全连接层将输出结果映射到0~1。
综上,预测总流程为:首先利用快速傅里叶变换,将轴承原始振动时域信息转换为频域信息;再用PVC-CAE模型提取特征;最后构建LSTM模型进行轴承寿命预测。整体预测框架如图6所示。
3 实验验证
3.1 实验数据
本文所使用的轴承全寿命周期数据来源于电气和电子工程学会(IEEE)2012年举办的PHM挑战赛[7],数据采集自PRONOSTIA测试平台,如图7所示。传感器的采样频率为25.6 kHz,每间隔10 s采集一次,每次采集的持续时间为0.1 s。数据集共包含三种工况下17个滚动轴承的振动数据,分别命名为轴承1_1~1_7、轴承2_1~2_7、轴承3_1~3_3。本文从每个工况中随后选择了几个轴承进行实验,其中轴承1_3和2_4依次作为测试轴承,其余作为训练集轴承。表1为实验轴承的介绍,表2为不同工况描述。
3.2 模型参数
Bearing1-3作为测试轴承时,举例说明模型参数的设置。从11个轴承中抽取Bearing1-3作为测试集,其余10个轴承作为训练集,将每个训练轴承的频域数据纵向均分为50份,剩余寿命标签间隔为0.02,PVC-CAE网络的batchsize计算得302,并根据输入数据的长度尺寸,特征提取模型的参数设置如表3所示。将302×1 280的频域特征压缩为302×160的隱藏特征,计算并行方差约束时将隐藏特征降采样为10个5×160的数组。
在PVC-CAE模型中,惩罚系数β用于调节隐层特征并行方差约束项的损失函数和重构损失之间的权重比例。β过小,训练时模型主要对重构损失进行优化,模型的权值便会朝着减小重构损失的方向进行调整,无法对隐层特征施加并行方差约束的作用;β过大,则主要对并行方差约束项的损失函数进行优化,会导致重构损失过大,出现特征提取不理想的情况。通过对重构损失与并行方差约束项的损失函数进行预计算,对β值进行了调试,在数量级10-5左右时能取得较好结果,本文取1×10-5进行实验。
LSTM预测模型中,四层LSTM隐藏层节点分别设置为200,120,40,10,步长设定为5。
3.3 特征差异性分析
PVC-CAE模型在CAE网络的重构损失上增加了一个并行方差约束,目的是在自动提取特征的同时减小同标签特征的轴承个体差异。为了验证PVC-CAE模型在促进同标签特征一致性上的有效性,与不加并行方差约束的普通卷积自编码网络进行对比,网络采用相同的参数。以Bearing1-3作为测试集时,其余轴承作为训练集,由于文章篇幅有限,训练集的三个工况下都只选择了一个轴承来展示,分别为Bearing1-1、2-4和3-1。寿命标签选择了0.2、0.6和0.9三种,以对应轴承退化的早期退化、中期退化和急剧退化三个阶段。即Bearing1-1的第560、第1 681和第2 522次采集信号;Bearing2-4的第150、第150和第675次采集信号;Bearing3-1的第103、第309和第463次采集信号。
在处理数据时,先将原始时域信号转换为频域信号,再利用深度学习模型提取隐层特征。时域信号和频域信号的状态在很大程度上决定了后续隐层特征的状态。为了在不同特征形式下体现同标签特征的轴承个体差异性,同时展示了各寿命标签所对应的时域特征和频域特征。图中时域信号特征的数据长度为2 560,频域信号特征的数据长度为1 280,隐层特征为160。具体如图8~10所示。
从时域特征图8(a)、9(a)和10(a)中可以直观地看出,尽管寿命标签相同,但三个轴承的时域特征整体上并不相同。频域特征图8(b)、9(b)和10(b)中也显示出,不同轴承峰值所对应的频带不一致,而频域特征中峰值的位置对于剩余寿命的预测结果是至关重要的。因此得到一个显然的结论:在时域和频域信息中,同寿命标签的时域特征和频域特征在不同轴承上具有差异。
图8(c)、9(c)和10(c)分别显示了在寿命标签0.2、0.6和0.9下CAE提取的隐层特征,在不同轴承隐层特征的对比下可以看出,在同寿命标签时,三个轴承的隐藏特征也是具有差异的。尤其是在数值序号0~20和110~130时,三个轴承的隐层特征差异明显,并且随着退化的加剧,这两部分区间隐层特征的差异也逐步增加。图8(d)、9(d)和10(d)为PVC-CAE模型提取的隐层特征,与CAE提取的隐藏特征进行对比,明显发现隐藏特征差异降低了,特征趋势线有很强的一致性。在数值序号0~20和110~130内,隐藏特征差异也显著降低。整个现象说明,PVC-CAE模型提取特征的确有利于减小同标签特征的轴承个体差异。
3.4 实验结果分析
为了验证PVC-CAE网络所提特征有利于减小预测误差,设置了与卷积自编码特征的对比实验,预测模型均采用相同参数的LSTM网络,同时与另外两种参考方法WTRVM[17]和多尺度[18]进行对比。测试轴承为bearing1-3和bearing2-4,其预测结果分别如图11和12所示,每个图中都显示了四种方法的预测结果。图中横坐标为采样序号,可以转换为轴承当前已运行时间,纵坐标为预测的轴承剩余寿命百分比,绿色实线为真实的寿命值,其他线条为各种方法的预测结果(见电子版)。同时将轴承急剧退化期的预测结果进行了局部放大处理,子图位于右上角。
从图11和12可以看出,无论是在bearing1-3还是2-4中,本文方法相比CAE-LSTM预测效果有所提升,更加接近真实的寿命线。在轴承的不同退化阶段,本文方法预测精度都在一定程度上优于CAE-LSTM,尤其在轴承的退化后期,有明显的提升。此现象也证明了前文中的猜想:同标签特征的轴承个体差异影响后续模型预测精度,PVC-CAE模型在轴承退化后期显著地减小了差异,预测精度也得到了显著的提升。再对比其余两种参考方法,本文方法也是明显优于它们的,尤其是对比WTRVM[17]方法,预测精度有大幅度提升。为了量化对比四种方法的预测结果,按照式(8)对四种方法预测结果的平均误差emean进行了计算,计算结果如表4所示。
对表4中的数据进行分析,可以看出本文方法的平均误差是最低的。在bearing1-3的结果中,本文方法的平均误差相比于CAE-LSTM、WTRVM[17]和多尺度[18]分别下降了66.7%、63.8%和64.8%;对于bearing2-4,分别下降了37.6%、76.1%和64.7%。结果表明本文方法是有效的,有利于提升轴承剩余寿命的预测精度。
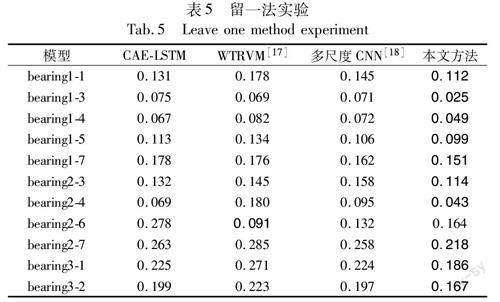
3.5 留一法实验
为了更全面地验证本文方法的有效性和适用性,采用留一法进行预测实验。留一法即每次只采用一个轴承作为测试集,其余轴承作为训练集,模型训练完毕后,利用测试集进行测试。四种模型的平均误差emean如表5所示,已在表中将最优的实验结果进行加粗标识。
分析表5和图13发现11组实验中有10组实验结果,本文方法的预测误差都是最低的,在不同的工况下均有一定效果,这说明对卷积自编码进行改进后并没有减弱原有模型的鲁棒性,PVC-CAE网络泛化性良好。
3.6 泛化性验证
为了进一步研究本文方法的通用性,在XJTU-SY数据集[19]上进行验证。实验共设计了三类工况,每类工况下有五个轴承。实验中设置采样频率为25.6 kHz,采样间隔为1 min,每次采样时长为1.28 s。數据采集时获取了水平方向和垂直方向的振动信号,本文在水平方向振动信号上使用留一法进行实验。实验结果如表6所示。
从表6中可以看出,本文方法在15组测试轴承实验中,有10组实验结果是优于其他三种对比方法的,同时本文方法所有实验结果的预测误差都低于CAE-LSTM方法,以上现象说明本文方法在XJTU-SY数据集也表现出了良好的效果。综上,整体归纳可以得知本文方法在不同的数据集上都有较好的适用性。已在表6将四种方法中最好的预测结果进行加粗显示。
4 结束语
在提取特征时,由于不同训练轴承的退化过程是不同的,同标签特征的轴承个体差异会影响后续模型的预测精度。为了解决这个问题,本文提出了一种基于PVC-CAE的轴承剩余寿命预测方法。通过对实验结果的分析,得到以下结论:
a)通过对同标签特征可视化,PVC-CAE模型可以有效降低同标签特征的轴承个体差异。用此特征进行预测,后续预测模型的预测精度有明显提升。
b)本文方法相比所参考预测方法,预测精度均有一定提升,同时在不同的数据集、不同的工况上也表现出了较好的适用性,证明了本文方法泛化性良好。
参考文献:
[1]Ma Meng,Mao Zhu.Deep-convolution-based LSTM network for remaining useful life prediction[J].IEEE Trans on Industrial Informa-tics,2020,17(3):1658-1667.
[2]Meng Zong,Li Jing,Yin Na,et al.Remaining useful life prediction of rolling bearing using fractal theory[J].Measurement,2020,156(C):107572.
[3]Lei Yaguo,Li Naipeng,Guo Liang,et al.Machinery health prognostics:a systematic review from data acquisition to RUL prediction[J].Mechanical Systems and Signal Processing,2018,104:799-834.
[4]郭亮,李長根,高宏力,等.大数据背景下基于特征学习的机械设备剩余寿命预测 [J].西南交通大学学报,2021,56(4):730-735,768.(Guo Liang,Li Changgen,Gao Hongli, et al.Residual life prediction of mechanical equipment based on feature learning in the background of big data [J].Journal of Southwest Jiaotong University,2021,56(4):730-735,768.)
[5]Singh J,Darpe A K,Singh S P.Bearing remaining useful life estimation using an adaptive data-driven model based on health state change point identification and K-means clustering[J].Measurement Science and Technology,2020,31(8):085601.
[6]Cheng Cheng,Ma Guijun,Zhang Yong,et al.A deep learning-based remaining useful life prediction approach for bearings [J].IEEE/ASME Trans on Mechatronics,2020,25(3):1243-1254.
[7]Nectoux P,Gouriveau R,Medjaher K,et al.PRONOSTIA:an experimental platform for bearings accelerated degradation tests [C]//Proc of IEEE International Conference on Prognostics and Health Management.Piscataway,NJ:IEEE Press,2012.
[8]王奉涛,陈旭涛,柳晨曦,等.基于KPCA和WPHM的滚动轴承可靠性评估与寿命预测 [J].振动、测试与诊断,2017,37(3):476-483,626.(Wang Fengtao,Chen Xutao,Liu Chenxi,et al.Reliability evaluation and life prediction of rolling bearing based on KPCA and WPHM [J].Journal of Vibration and Vibration,2017,37(3):476-483,626.)
[9]申中杰,陈雪峰,何正嘉,等.基于相对特征和多变量支持向量机的滚动轴承剩余寿命预测 [J].机械工程学报,2013,49(2):183-189.(Shen Zhongjie,Chen Xuefeng,He Zhengjia,et al.Remaining life prediction of rolling bearings based on relative feature and multivariable support vector machine [J].Journal of Mechanical Engineering,2013,49(2):183-189.)
[10]Li Yaolong,Li Hongru,Wang Bing,et al.Research on the feature selection of rolling bearings degradation features [J].Shock and Vibration,2019,2019(1-2):1-19.
[11]康守强,叶立强,王玉静,等.基于MCEA-KPCA和组合SVR的滚动轴承剩余使用寿命预测 [J].电子测量与仪器学报,2017,31(9):1365-1371.(Kang Shouqiang,Ye Liqiang,Wang Yujing,et al.Prediction of remaining service life of rolling bearing based on MCEA-KPCA and combined SVR[J].Journal of Electronic Measurement and Instrument,2017,31(9):1365-1371.)
[12]Kaji M,Parvizian J,Venn H.Constructing a reliable health indicator for bearings using convolutional autoencoder and continuous wavelet transform[J].Applied Sciences,2020,10(24):8948.
[13]Lin Pengfei,Tao Jizhong.A novel bearing health indicator construction method based on ensemble stacked autoencoder [C]//Proc of IEEE International Conference on Prognostics and Health Management.Piscataway,NJ:IEEE Press,2019.
[14]張继冬,邹益胜,蒋雨良,等.基于全卷积变分自编码网络FCVAE的轴承剩余寿命预测方法 [J].振动与冲击,2020,39(19):13-18,25.(Zhang Jidong,Zou Yisheng,Jiang Yuliang,et al.Prediction of bearing residual life based on FCVAE full convolution variational autocoding network[J].Journal of Vibration and Shock,2020,39(19):13-18,25.)
[15]曾大懿,蒋雨良,邹益胜,等.一种新的轴承寿命预测特征评价指标构建与验证[J].振动与冲击,2021,40(22):18-27.(Zeng Dayi,Jiang Yuliang,Zou Yisheng,et al.Construction and validation of a new characteristic evaluation index for bearing life prediction[J].Journal of Vibration and Shock,2021,40(22):18-27.)
[16]Ding Ning,Li Huning,Yin Zhongwei,et al.Journal bearing seizure degradation assessment and remaining useful life prediction based on long short-term memory neural network[J].Measurement,2020,166:108215.
[17]Tang Jian,Zheng Guanhui,He Dong,et al.Rolling bearing remaining useful life prediction via weight tracking relevance vector machine[J].Measurement Science and Technology,2021,32(2):024006.
[18]马占伟,袁逸萍,樊盼盼,等.基于多尺度卷积神经网络的轴承剩余寿命预测[J].机械设计与制造,2023,3(1):5-8.(Ma Zhanwei,Yuan Yiping,Fan Panpan,et al.Based on multi-scale convolution neural network bearing the residual life prediction[J].Journal of Mechanical Design and Manufacturing,2023,3(1):5-8.)
[19]Wang Biao,Lei Yaguo,Li Naipeng,et al.A hybrid prognostics approach for estimating remaining useful life of rolling element bearings[J].IEEE Trans on Reliability,2020,69(1):401-412.
收稿日期:2023-02-10;修回日期:2023-04-13
作者简介:张远亮(1988-),男(通信作者),四川成都人,讲师,硕士,主要研究方向为车辆振动模态、机械设备运维(2841027236@qq.com);李海浪(1995-),男,四川广安人,硕士,主要研究方向为机械设备运维.
