基于Prim-DMGA算法的闭环供应链网络鲁棒优化研究

孙军艳　陈泽飞　陈智瑞　李晓朋

摘 要：针对不确定环境下的闭环供应链网络优化问题，在需求不确定及设施中断风险的条件下，基于鲁棒对等优化方法建立了一种以闭环供应链网络总成本最小为目标的鲁棒优化模型，以解决供应链网络中的不确定性问题，并提出了Prim-DMGA。首先基于Prim算法得到高质量的初始种群，其次让路径规划方案和设施选址方案在两层自适应GA的不断反馈中达到最优。实验结果表明，Prim-DMGA得到的目标函数值优于单层Prim-MGA与传统GA，且在求解大规模算例时，求解结果优于CPLEX软件。研究结论表明，Prim-DMGA能以较少的计算时间获得质量更优的解，鲁棒优化模型可以有效减少不确定因素带来的不利影响，提高闭环供应链网络的鲁棒性能。

关键词：闭环供应链网络； 需求不确定； 设施中断风险； 鲁棒优化； Prim-DMGA算法

中图分类号：TP302 文献标志码：A 文章编号：1001-3695（2023）10-016-2984-09

doi：10.19734/j.issn.1001-3695.2023.02.0087

Robust optimization of closed-loop supply chain network based on Prim-DMGA algorithm

Sun Junyan， Chen Zefei， Chen Zhirui， Li Xiaopeng

（School of Mechanical & Electrical Engineering， Shaanxi University of Science & Technology， Xian 710021， China）

Abstract：This paper proposed a robust peer-to-peer optimization method in the context of uncertain environments to address the uncertainty in closed-loop supply chain networks while considering demand uncertainty and facility disruption risk. This paper formulated a robust optimization model to minimize the total cost of the closed-loop supply chain network. Additionally， this paper proposed a Prim-DMGA that firstly identified high-quality initial solutions using the Prim algorithm and then optimized the routing and facility selection solutions in a two-layer adaptive GA feedback loop. The experimental results demonstrate that the Prim-DMGA generates better objective function values than the single-layer Prim-MGA and traditional GA with less computational time. Further， the results obtained from the algorithm are superior to those obtained by using the CPLEX software in solving large-scale scenarios. It concludes that the proposed robust optimization model effectively reduces the adverse effects caused by uncertainty and improves the robustness of closed-loop supply chain networks. Moreover， the Prim-DMGA generates better solutions with less computational time.

Key words：closed-loop supply chain network; demand uncertainty; facilities disruption risk; robust optimization; Prim-DMGA

0 引言

近年來，随着全球化进程的不断推进，企业面临的竞争越来越激烈，不仅要面临复杂多变的市场竞争环境和社会环境，还要面临无法预知的不确定风险与挑战。因此，研究不确定环境下的闭环供应链网络的鲁棒性能，对于提高供应链应对不确定风险的能力、降低运作成本、增强环境友好性具有一定的理论和实际意义。

国内外学者对于不确定环境下的闭环供应链网络的研究方向多集中在成本、价格、需求等运营过程中参数不确定方面。Azizi等人［1］考虑需求及利润的不确定性，针对逆向物流网络优化问题建立了两阶段随机规划模型。Goodarzian等人［2］考虑设计参数中设施建设、运输、库存持有成本的不确定性，针对药品供应链网络问题建立了双目标混合整数模糊规划模型。Yu等人［3］考虑了客户需求、退货率和退货品质量的不确定因素，针对选址问题建立了模糊随机多目标优化模型。Pudasaini［4］基于需求不确定的供应链网络优化问题，以运输成本及产品损失成本最小，为目标建立了多目标两阶段随机规划模型。You等人［5］在考虑需求和运费不确定的情况下，建立以总成本最小为目标的两阶段随机规划模型。Peidro等人［6］采用三角模糊数描述需求、成本和供应的不确定性，建立以采购、库存、运输成本最小为目标的混合整数模糊规划模型。以上研究在考虑供应链网络中的不确定因素上，只考虑运营过程中参数的不确定，而忽略了突发事件的不确定性对供应链网络的影响。

部分学者在考虑供应链网络运营过程中参数不确定时，同时考虑了供应链网络中突发事件的不确定性因素。Tolooie等人［7］考虑了客户需求不确定与设施中断的影响，建立了两阶段随机混合整数规划模型。Vali-Siar等人［8］针对设施中断风险和成本不确定性的供应链网络问题，利用模糊随机规划方法建立了多目标的模糊随机混合规划模型。Yin等人［9］采用情景法描述不确定需求与中断情景，设计了总成本最小的两阶段随机优化模型。王振等人［10］针对闭环物流网络中需求和回收品质量不确定问题以及供应中断的影响，建立了总成本最小的模糊机会约束模型。狄卫民等人［11］考虑两级设施中断与需求不确定的情况，建立总成本最小化的随机规划模型。以上学者在考虑供应链网络中的不确定因素上，同时考虑了运营过程中参数的不确定和突发事件的不确定性对供应链网络的影响，但是他们在供应链优化问题中，采用随机规划、模糊规划方法来解决供应链网络中的不确定性问题，仍具有一定的局限性。

鲁棒优化的核心思想是求得所有参数在最坏情形下的最优解，用集合的形式对不确定参数进行描述，不增加问题求解的复杂性。Bertsimas等人［12］针对不确定环境下的闭环供应链网络优化问题，在2004年提出了一种新的鲁棒优化方法，即每个不确定参数只需简单用一个具体区间来表示，且可以通过最小最大方法来保证解的可行性，该方法被广泛应用于不确定问题的优化研究中。于冬梅等人［13］采用文献［12］的鲁棒优化方法，建立以最小设施选址及运输成本为目标的鲁棒优化模型，并采用蝙蝠算法求解。Gholizadeh等人［14］以网络总利润最大为优化目标，构建需求不确定的情景鲁棒优化模型，结果表明该模型可以有效地应对需求和供应不确定性对网络的影响。Attia［15］采用情景法描述石油市场需求及价格的不确定性，建立石油供应链网络鲁棒优化模型，结果表明，与确定性、随机规划以及基于风险的建模方法相比，鲁棒优化模型能源消耗率较高、成本较低。邱若臻等人［16］建立以供应链绩效最大为目标的鲁棒优化模型，数值仿真验证模型在需求和成本的扰动下仍表现出良好的鲁棒性。董海等人［17］采用多面体鲁棒优化方法设计多目标鲁棒优化模型，其结果表明，多面体鲁棒优化模型能有效降低不确定因素带来的不利影响。

不确定供应链网络优化问题需要考虑的变量及约束条件较多，已被证明为NP-hard问题。目前该领域的最新研究多采用智能算法来求解此类问题。尉迟群丽等人［18］采用改进的禁忌搜索算法求解构建的集成优化模型，结果表明，改进的禁忌搜索算法在可接受的时间内得到的解质量更高。Abbassi等人［19］提出一种可变邻域搜索启发法改进多目标粒子群算法，可以在較短的时间内得出最优的设施布局及路径规划方案。Liao等人［20］分别采用遗传模拟退火算法、遗传算法、模拟退火算法求解，算例表明混合算法展现了更好的求解效果。Tirkolaee等人［21］设计一种多目标灰狼算法来求解多目标优化模型，结果表明多目标灰狼算法解的质量优于非支配排序遗传算法2%。Li等人［22］利用差分进化算法改进NSGA-Ⅱ变异算子，增加种群多样性与全局搜索性，实验表明改进算法提高了个体分布的均匀性。遗传算法（genetic algorithms，GA）是通过数学仿真模拟生物遗传学中自然进化的过程来寻找问题最优解的方法，被广泛用于求解供应链网络优化问题中。但传统GA普遍采用随机结构进行初始化种群选择，导致了选择种群极有可能不符合约束条件，从而降低种群质量与收敛速度。因此可将遗传算法与其他算法或理念相结合，以提高该算法的种群质量与收敛速度。

通过对上述文献的梳理发现，在不确定因素的考虑上，同时考虑运营过程中参数的不确定和突发事件不确定性的文献较少，且大多数学者只考虑宏观选址问题，微观层面的路径规划、流量分配等问题很少考虑；并且在模型求解方面，多数学者采用的传统启发式算法存在效率较低的问题。面对越来越复杂的市场环境，消费终端需求面临着极大的不确定性，本文将考虑闭环供应链网络消费终端需求量与退货量的不确定性与设施中断的影响，对闭环供应链网络设施选址、路径规划、物流量分配等问题进行集成优化研究。利用文献［12］的鲁棒优化方法处理不确定性因素，构建供应链网络总成本最小的鲁棒优化模型，针对传统遗传算法在选择种群过程中极有可能降低种群质量，使得算法陷入局部最优且过早收敛的情况，设计了Prim-DMGA求解模型，以提升供应链网络应对风险的能力，实现供应链网络降本增效，鲁棒性、经济效益的综合提升。

1 模型建立

1.1 问题描述

本文将研究由多个候选制造中心、多个候选配送中心、若干客户需求点组成的闭环供应链网络系统，如图1所示。其供应链网络运行如下：首先，产品由制造中心运至多个配送中心，再由配送中心运往各客户需求点；当客户提出退换货需求时，不满意的产品被退回并交由配送中心进行检查处理，再将需要返回制造中心的部分产品运至制造中心进行维修或再加工。其中，客户点的需求量与退货量处于不确定性的状态，且考虑制造中心的设施中断风险。

1.2 模型假设

a）客户需求为单一品种的产品。

b）候选制造中心、配送中心位置已知，且拥有足够的运输能力。

c）制造中心发生中断的概率不确定且相互独立，中断发生后制造中心剩余一定的生产能力，配送中心不存在中断风险。

d）客户位置已知，每个客户仅由一个配送中心为其服务；在为客户需求点提供正向配送服务的同时兼顾逆向收集退换货产品的服务。

e）退换货产品无质量缺陷，配送中心检查再包装后可重新进行销售。

1.3 符号说明

1） 集合说明

I为候选制造中心集合，i∈I；J为候选配送中心集合，j∈J；K为需求点集合，k∈K；S为制造中心设施中断情景集合，s∈S。

2）参数定义

Fi为制造中心i的建设成本；MFi为制造中心i每单位产品的生产成本；TCij为制造中心i到配送中心j的单位产品运输成本；αi为制造中心i的状态参数，制造中心i非中断状态工作为1，否则为0；pi为制造中心i发生设施中断的概率；bi为制造中心i中断发生后剩余产能补给能力的比例；Cmaxi为制造中心i的产能上限；disij为制造中心i到配送中心j的距离；disjk为配送中心j到客户需求点k的距离；Fj为配送中心j的建设成本；NFj为配送中心j每单位产品正向处理成本；VFj为配送中心j每单位产品的回收处理成本；TCjk为配送中心j到需求点k的单位运输成本；Cmaxj为配送中心j的产品处理能力上限；Cmaxjv为配送中心j的回收处理能力上限；dk为客户需求点k实际的市场需求量；ek为客户需求点k实际的退货产品数量。

3）决策变量

Vsij为情景s下制造中心i向配送中心j供应的产品数量;Vjk为配送中心j给客户k配送的产品数量;Zjk为配送中心j回收客户k的产品数量。

1.4 基本模型构建

以供应链网络总成本最小为目标，包括设施建设的固定成本、产品制造成本、产品正向处理成本和回收处理成本及产品运输成本。因此，目标函数可以表示为

式（2）中，第一项表示制造中心i固定建设成本；第二项表示配送中心j建设固定成本。式（3）表示情景s下制造中心i的产品制造成本。式（4）第一项表示配送中心j对产品的正向处理成本，包括产品的分拨、装箱成本；第二项表示配送中心j对产品的回收处理成本。式（5）中，第一项为制造中心i到配送中心j正向物流的运输成本，第二项为配送中心j到需求点k正向物流的產品运输成本，第三项表示需求点k到配送中心j逆向物流的产品运输成本。

式（6）代表只有选择建设的制造中心才向配送中心提供服务，式（7）代表只有选择建设的配送中心才向客户需求点提供服务；式（8）～（11）为网络物流平衡约束，式（8）代表制造中心供给配送中心的产品数量等于配送中心供给客户点的产品数量；式（9）（10）代表市场需求量与退货量全部被满足；式（11）代表配送中心回收客户点的产品数量都是其供给数量的一部分；式（12）～（14）为设施能力约束；式（12）代表制造中心供应产品数量不超过其生产能力上限；式（13）代表配送中心供应产品数量不超过其最大容量；式（14）代表配送中心回收产品数量不超过其最大服务能力；式（15）～（17）为车辆路径规划约束；式（15）（16）代表每个客户仅由一个配送中心为其服务；式（17）代表每个配送中心仅服务分配给该设施的客户；式（18）～（25）为决策变量约束。

2 不确定参数处理

2.1 不确定需求量与退货量处理

对于式（9）（10）中需求量dk、退货量ek，采用Box不确定集描述。假设每个客户需求点的需求量与退货量取值于有界的对称区间集合，定义dk∈［dk－dk^，dk+dk^］；ek∈［ek－ek^，ek+ek^］。其中，dk为需求量dk的名义值，dk^为需求量dk的变化范围，ek为退货量ek的名义值，ek^为退货量ek的变化范围。带有不确定参数的式（9）（10）可以进一步描述为

其中：m为发生中断的制造中心。

3 Prim-DMGA设计

3.1 Prim-DMGA设计框架

遗传算法是通过数学仿真模拟生物遗传学中自然进化的过程来寻找问题最优解的方法，是最为经典的一类智能优化算法。传统GA普遍采用随机结构进行初始化种群选择，这导致了选择种群极有可能不符合约束条件，从而降低种群质量与收敛速度。同时在进化过程中，在复杂的约束条件下，传统的交叉或变异方法可能会破坏掉优秀个体的基因结构，或是导致种群多样性丢失，使得算法陷入局部最优，过早收敛。

Prim算法运用了贪婪算法的思想，通过逐步扩大最小生成树中包含的节点数，寻找图中的顶点集合U和其补集顶点U-V之间权值最小的边，构建出边权值最小的一棵生成树。Prim算法只与图的顶点有关，与边数无关。

在供应链网络中，将制造中心、配送中心、客户点看成有向图G（V，E），V表示节点值，V=I∪J∪K，I、J、K分别表示制造中心、配送中心、客户点集合，E表示路径集，E={（i，j）|i，j∈V，i≠j}。制造中心、配送中心及客户点在有向图G上一一对应，则其中必然有一最小生成树能使供应链网络成本最低。基于这种思想，本文设计了Prim-DMGA，该算法在传统GA上引入Prim算法，改良了传统GA种群质量较低、种群收敛速度较慢的问题。

集设施选址、关系分配及路径规划决策的闭环供应链网络优化问题属于混合整数规划问题，在求解时难度较大。基于这种情况，本文设计的Prim-DMGA算法结构分为内外两层：外层采用Prim算法与自适应GA相结合的方式（Prim-MGA）得到选址及设施关系分配结果，内层自适应遗传算法（MGA）根据外层Prim-MGA得到的选址及设施规划方案进行路径单独编码优化。目标函数在内外层算法的不断反馈中得到最优解，达到降低搜索空间的同时不破坏模型整体性的目的。

算法的具体设计步骤如下：

a）随机产生设施选址与关系分配方案的初始化种群C0，种群大小为N1，计算种群内个体的适应度。

b）改善初始种群，基于Prim算法得到更新后的种群Ci，i=1，2，3，…，N1，令迭代次数t=0。

c）内层MGA优化配送路径。将Ci所对应的选址及关系分配方案独立编码作为输入参数传递给内层MGA，令Ci=Cn产生内层初始种群Cn（n=1，2，3，…，N2），种群大小为N2，令内层MGA的迭代次数g=0。

d）计算Cn适应度值f2，选择、自适应交叉遗传产生子种群Cn+1，判断是否符合停止条件g≥Gmax2，若是，停止运算，转向步骤f）；否则，令g=g+1，继续步骤d）。

e）判断Ci中所有配送中心是否都完成内层路径优化，若是，继续步骤f），否则，返回步骤c）。

f）计算Cn+1中个体适应度值f1，自适应遗传操作产生新子代，判断是否符合停止条件t≥Gmax1。如满足则停止运算，转向步骤g）；否则，令t=t+1，继续步骤f）。

g）输出最优规划方案。

Prim-DMGA的具体流程如图2所示。

3.2 外层Prim-MGA设计

1）编码及种群初始化

外层算法得到选址及设施关系分配结果，根据模型特点，采用0-1编码和实数编码两种方式对染色体进行编码，生成规模为N1的初始种群C0。每条染色体由4个基因段构成，基因段1、2为0-1编码，基因位代表设施编号，基因值为二进制串（0或1），表示制造中心、配送中心是否被选择。基因段3、4采用实数编码，基因位代表设施编号，第j个基因位表示制造中心i给配送中心j供应产品的量及配送中心j分配给需求点k产品的数量，具体编码方式如图3所示。

2）Prim算法改善初始种群设计

a）C0中每一个个体对应的配送中心、客户点形成的连通图为NG=（V1，e1），V1=J∪K，e1={（j，k）|j，k∈V1，j≠k}，从J中随机选择一个点j作为顶点，放入生成树节点集U1中，选择边权值最小的节点k加入到最小生成树节点集U1，从V1中删去j、k。循环该过程，直至所有的客户点k被分配给配送中心j。

b）判断配送中心运输至客户点的产品数量以及回收的产品数量是否满足需求，即式（9）与（10），若是，得到由配送中心、需求点组成的N个最小生成树，最小生成树集UN={U1，…，UN}，否则，重复步骤a）。

c）记由制造中心、配送中心、客户点形成的连通图NT=（V2，e2），V2=I∪UN，e2={（i，j）|i，j∈V2，i≠j}，从UN随机选择一个生成树放入节点集合S1，选择与这个顶点边权值最小的节点i加入S1，从V2中删去i、UN，直至所有的制造中心i分配给UN。

d）判断制造中心运输至配送中心产品数量是否满足约束，即式（8）。若是，得到由制造中心、配送中心、需求点组成的N个最小生成树SN={S1，…，SN}，否则重复步骤c）。

3）遗传操作

a）适应度计算。在外层算法中，设适应度函数为总目标函数的倒数，方案总成本越小个体适应度越高，计算公式为

b）选择算子。采用轮盘赌法，每个个体被选中的概率与适应度成正比，适应度越高，被选中的概率越大，设pi为第i个个体被选中的概率，则

c）自适应交叉、变异操作。假设种群中有N个个体，每个个体有M位基因，用一个N×M的矩阵表示该种群，计算第m列元素的标准差dm，表示第m列基因在该种群中的差异度：

其中：f′是适应度值较大的交叉个体的适应度值;f是适应度值较大的变异个体的适应度值;fave是种群平均适应度值。pc1>pc2，pm1>pm2 ，当个体适应度较小或种群相异度较小时，交叉变异概率较大，增加种群多样性，避免陷入局部最优或过早收敛。

d）终止条件。按照以上步骤循环操作，当达到最大遗传代数Gmax2时终止算法，得到选址及服务关系分配方案。

3.3 内层MGA设计

1）编码

内层算法进行路径优化，采用自然数编码。按外层方案中配送中心对应的客户点总数生成m位基因，对配送中心和客户点依次进行编码：1，2，3，4，5，…，m。假设有5个配送中心，编号依次为1～5，10个需求点编号为6，7，8，…，15。一条完整个体编码形式为3→12→15→3，则表示为从配送中心3出发，依次经过了需求点12和15，最后返回配送中心3。具体编码方式如圖4所示。令种群大小为N2，迭代次数g=0。

2）适应度计算

内层算法中，设适应度函数f2为配送中心至需求点的运输成本的倒数，即方案运输成本越小，个体适应度越高。计算公式为

3）遗传操作

采用轮盘赌法，每个个体被选为父代的概率与其适应度成正比；采用自适应交叉变异算子。

4）终止条件

按照以上步骤循环操作，当达到最大遗传代数Gmax2时终止算法，得到最优路径方案。

4 算例分析

为了验证不确定环境下的鲁棒优化模型和Prim-DMGA的有效性，以某企业自营家电品牌为案例背景，进行算例分析。

4.1 算例描述

某企业自营家电品牌根据品牌发展战略，欲拓展新的消费市场，企业筛选出三套算例进行分析：a）算例1筛选出3个制造中心，6个配送中心作为候选设施节点，12个客户点（即客户群）；b）算例2筛选出6个制造中心，12个配送中心作为候选设施节点，20个客户点（即客户群）；c）算例3筛选出20个制造中心，36个配送中心作为候选设施节点，96个客户点（即客户群）；各候选设施点位置及客户点位置已知，不同制造中心的建设成本、生产能力、生产成本、与配送中心的单位运输成本及中断概率是不同的。供应链网络参数值设置如表1、2所示。

4.2 算法有效性分析

求解模型运行在16 GB内存、IntelCoreTMI7-8550u CPU 1.80 GHz处理器的Windows上，将表1、2中的参数代入模型，对三套算例进行了四种测试。首先使用 CPLEX 软件去求解模型，由于CPLEX收敛速度较慢，所以对CPLEX设置了最大运行时间，按照算例规模，分别设置为1 200 s、1 800 s和2 400 s，以便更快求出问题解。其次采用MATLAB R2021b编程计算，在相同软硬件环境下，将传统GA、外层Prim-MGA（即不对路径进行单独编码优化）及Prim-DMGA各运行20次进行对比实验。

首先使用算例1规模进行测试，最终CPLEX的求解结果与算法运算结果如表3所示，迭代图如图5所示。

由表3可知，计算算例1方案时，CPLEX软件求解的最优目标函数值最小，传统GA求得的最优目标函数值最大， Prim-DMGA求得的最优函数值解的质量优于外层Prim-MGA；且Prim-DMGA运行20次得到的平均目标函数值解的质量较外层Prim-MGA求得的平均目标函数值提升2.88%，较传统GA提升5.85%。虽然CPLEX软件求解时间过长，但是求解结果较Prim-DMGA解的质量提升1.69%。在算法运行时间方面，因为CPLEX软件求解规模越大，收敛速度越慢，所以设置最大运行时间为1 200 s，而由于初始解质量较高，Prim-DMGA与外层Prim-MGA搜索效率均较高，运行时间明显优于传统GA。相对地，与外层Prim-MGA相比，Prim-DMGA的运行时间较长，但却获得了质量更高的解。

由图5可知，CPLEX求解器求解在第80代左右获得最优化解，GA在第63代左右获得最优解，Prim-MGA在35代左右获得最优解，Prim-DMGA在42代左右收敛。

其次使用算例2规模进行测试，最终CPLEX的求解结果与算法运算结果如表4所示，迭代图如图6所示。

由表4可知，当算例规模变大，即算例2规模经过1 800 s的计算，CPLEX软件求解的最优目标函数值解的质量优于传统GA，弱于外层Prim-MGA与Prim-DMGA，其中Prim-DMGA得到的最优值最小，且Prim-DMGA运行20次得到的平均目标函数值解的质量较外层Prim-MGA求得的平均目标函数值提升2.91%，较传统GA提升5.89%。Prim-DMGA求得的最优目标函数值较CPLEX软件提升2.84%。同样地，Prim-DMGA与外层Prim-MGA搜索效率均较高，运行时间明显优于传统GA。

由图6可知，CPLEX求解器求解在第79代左右获得最优化解，GA在第62代左右获得最优解，Prim-MGA在35代左右获得最优解，Prim-DMGA收在40代左右收敛，Prim-DMGA能以较少的迭代次数获得质量更优的解。

最后使用算例3的规模进行测试，最终CPLEX的求解结果与算法运算结果如表5所示，迭代图如图7所示。

由表5可知，计算算例3方案时，由于计算规模过大，CPLEX软件求解的最优目标函数值最大，其次为传统GA， Prim-DMGA求得的最优函数值小于外层Prim-MGA，且Prim-DMGA运行20次得到的平均目标函数值解的质量较外层Prim-MGA求得的平均目标函数值提升2.53%，较传统GA提升6.01%。Prim-DMGA求得的最优目标函数值解的质量较CPLEX软件提升7.49%。在算法运行时间方面，因为CPLEX软件求解规模越大，收敛速度越慢，所以设置最大运行时间为2 400 s，Prim-DMGA与外层Prim-MGA搜索效率均较高，运行时间明显优于传统GA。

由图7可知，CPLEX求解器求解在第80代左右获得最优化解，GA在第65代左右获得最优解，Prim-MGA在35代左右获得最优解，Prim-DMGA在41代左右收敛，Prim-DMGA能以较少的迭代次数获得质量更优的解。

由此可知，CPLEX软件在求解小规模算例更有优势，但是运行时间过长、收敛速度过慢。随着算例规模的增加，Prim-DMGA表现出更好的优势，且运行时间少于CPLEX求解器与传统GA。

4.3 结果分析

结果分析选取算例2的方案，基于Prim-DMGA，计算出算例2规模的供应链最佳网络规划和流量分配方案，如图8～11所示。图形中的数字代表被选入供应链网络的节点编号，线条代表节点之间建立产品供应关系或回收关系，线条上的数字代表节点之间分配的产品流量。

由图8、9可知，Γdk=0，Γek=0时，即确定型网络模型时，闭环供应链网络选择建设制造中心数量为5，编号分别为1，3，4，5，6；配送中心数量为5，分别为1，3，7，10，12。例如由制造中心1向配送中心1供應6 522件产品，由配送中心1为客户点3，13，11，4依次提供服务。

由图10、11可知，Γdk=20，Γek=20时，选择建设的制造中心编号分别为1，2，3，4，5，6；选择建设配送中心编号分别为1，4，7，11，12，选择建设制造中心的数量比确定性网络增加了一个；选择建设配送中心数量与确定性网络相同，但布局方案不同，关系分配及路径规划方面也发生了变化，例如由制造中心2，3向配送中心7总共供应7 986件产品，由配送中心7为客户点10，8，14，9依次提供服务。

情景1为制造中心正常供应情况。情景2为一个制造中心发生设施中断的情景，设施节点间关系分配结构不变，节点间物流量发生一定变化。情景3中制造中心3、5发生设施中断，设施节点间关系分配及物流量均发生一定变化，此时选择制造中心2、4为配送中心7分别补充供应产品数量887、955件，制造中心6为配送中心12补充供应1 957件。情景4中制造中心2、3、5发生中断，选择制造中心1为配送中心4补充供应969件产品。选择制造中心4、6为配送中心7补充供应2266、887件产品。选择制造中心4、6为配送中心12补充供应805、1152件。

由图12可知，在相同的不确定程度下，不同的中断情景，设施选址虽然一致，但关系分配、节点间产品流量决策有明显的差异。当中断的制造中心数量增加时，通过其他制造中心补充供应数量增加，决策者可采取不同的运作方案保证网络有效运行，减少设施中断对供应链网络造成的影响。

4.4 灵敏度分析

4.4.1 不确定参数灵敏度分析

为探究不确定程度对网络规划方案的影响，基于算例2的结果分析，令需求量不确定程度控制参数Γdk=0、4、8、12、16、20，退货量不确定程度控制参数Γek=0为第一组实验；Γdk=0，Γek=0、4、8、12、16、20为第二组实验。基于算例2方案，采用Prim-DMGA求解模型，令γ=Γdk/K，β=Γek/K，分别代表需求量及退货量的不确定程度，得到不同不确定程度下网络设施选址方案如表6、7所示，网络总成本随不确定程度变化趋势如图13和14所示。

由表6可知，当退货量不确定程度不變，需求量不确定程度γ增加时，对制造中心I、配送中心J的数量和布局均有一定影响。当γ<0.6时，建设制造中心数量为5；当γ≥0.6时，建设制造中心的数量增加到6；当γ∈［0，1］时，配送中心的数量均为5，但布局发生一定变化。例如，γ=0.4与γ=0.2相比，制造中心选址均为1，2，3，5，6，配送中心选址均为1，4，7，10，12。当γ=0.6时，制造中心的数量增加，制造中心选址为1，2，3，4，5，6，配送中心选址没有变化。

由表7可知，当需求量不确定程度不变，退货量不确定程度β增加时，对配送中心的布局有一定影响，对设施选址数量影响不大。例如β=1与β=0相比，制造中心数量均为5，编号为1，3，4，5，6，配送中心的数量均为5，但布局方案发生变化，当β=1时配送中心变为2，4，7，11，12。

由图13可知，网络总成本随γ的增加而增加。当γ=0.6时，网络总成本增幅较为明显，网络总成本增幅为10.16%。这是因为，此时网络通过增加设施选址数量来满足由于制造中心中断所造成的供给短缺，设施选址成本增加。当γ持续增加时，网络总成本增幅放缓，此时网络通过增加生产、运输成本维持系统鲁棒性能。

由图14可知，网络总成本随β的增加而增加，但网络总成本增幅较小。当β=1时，网络总成本增幅0.52%，这是因为当退货量不确定程度增加时，网络仅通过增加回收处理成本和运输成本维持系统鲁棒性能。由此可以得出结论，需求量不确定程度对网络总成本的影响较大。

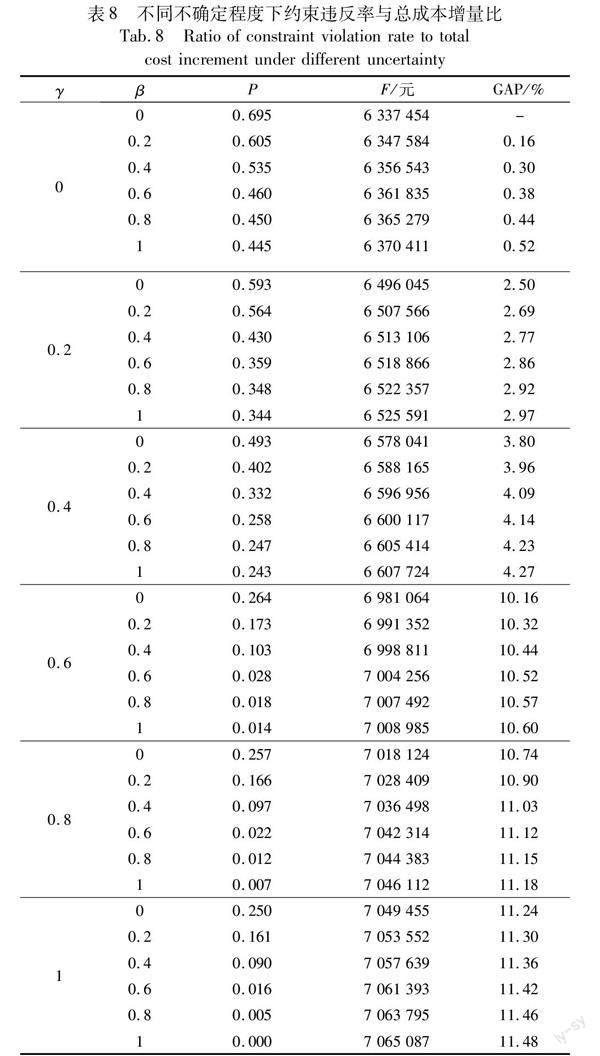
为探究模型鲁棒性、约束违反概率以及经济成本之间的关系，记P为约束式（9）和（10）的违反概率，GAP为总成本增量比，表达式如（57）和（58）所示。

其中：Frob为由鲁棒优化模型确定的供应链网络的成本值;FSC为确定模型（Γdk=0，Γek=0）的网络总成本。令Γdk、Γek分别等于0、4、8、12、16、20，共产生36种不确定程度控制参数组合，不同不确定程度下约束违反概率、网络总成本及总成本增量比，如表8所示。

由表8可知，无论是γ或β的增加，都会使约束违反概率降低，也会使网络总成本增加。即当网络不确定程度较高时，决策者作出了更加保守的决策，使得网络的约束违反概率降低，网络鲁棒性增强，但决策结果可能过于保守导致网络总成本增加过大。

在这样的情况下，决策者可以根据表8中不同不确定程度组合对其约束违反概率与总成本进行权衡后作出决策，或是根据期望总成本和期望约束违反概率设置不确定程度得到网络最佳规划方案。例如当决策者希望约束违反概率小于5%时，即γ≥0.6或β≥0.6时，可将模型中不确定程度控制参数组合中Γdk、Γek设置为12、16、20得到约束违反概率小于5%的最佳闭环供应链网络规划方案。

综上，在实际应用中，决策者可以根据不确定环境的实际情况，灵活调整不确定程度控制参数，寻找经济成本与鲁棒性相协调的网络结构，实现闭环供应链网络经济性与鲁棒性的综合提升。

4.4.2 设施中断不确定参数灵敏度分析

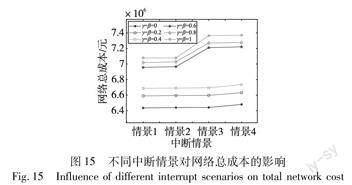
为探究不同不确定程度的需求量与设施中断对网络造成的影响，基于算例2方案的结果分析，在不确定程度控制参数Γdk=Γek=0，4，8，12，16，20，即γ=β=0，0.2，0.4，0.6，0.8，1时，分析各中断情景发生对网络总成本的影响，结果如图15所示。

由图15可知，当γ=β≤0.4时，不同的中断情景对网络的总成本影响不大。当γ=β>0.4时，从情景2到3，即设施中断数量从1个增加到2个时，网络总成本增加。其中，γ=β=0.6时增加了3.74%，γ=β=0.8时增加了3.96%，γ=β=1时增加了4.15%。因此，决策者可将设施中断的比例控制在40%以内，保证网络运营成本在可控的范围之内。

由此可见，需求不确定与设施中断的叠加影响下，网络规划方案有着较大的差异，决策者可以根据对需求不确定与设施中断的风险偏好设置最优的网络规划方案，选择产能充足的制造中心加入供应链网络以满足市场需求，对未来可能发生的设施中断风险时，决策者可采取不同的运作方案保证网络有效运行。

5 结束语

本文针对需求量、退货量的不确定性以及设施中断的影响，构建了以供应链网络总成本最小为目标的鲁棒优化模型；并设计了Prim-DMGA，得到不同不确定程度控制参数和不同设施中断情景下的最优网络规划方案。结果表明：

a）Prim-DMGA得到的目标函数值优于单层Prim-MGA与传统GA，且在求解大规模算例时，求解结果优于CPLEX软件。证明了该算法在求解闭环供应链网络优化问题时具有一定的优越性。

b）在需求量、退货量不确定与设施中断风险的叠加影响下，不确定程度控制参数对网络设施选址、流量分配及路径规划均有一定影响，其中不确定的需求量对设施选址的数量影响明显。

c）鲁棒优化模型可以有效减少不确定因素带来的不利影响，决策者可以通过实际需求设置合理的不确定程度控制参数，权衡闭环供应链网络的经济性与鲁棒性，得到最佳闭环供应链网络规划方案。

综上所述，本文设计的Prim-DMGA能以较少的计算时间获得质量更优的解，鲁棒优化模型可以有效减少不确定因素带来的不利影响，提高闭环供应链网络的鲁棒性能。今后的研究工作拟从以下三方面展开：a）响应国家低碳政策，考虑闭环供应链网络经济效应和环境效应建立双目标鲁棒优化模型；b）在考虑市场需求量及退货量的不确定性时，同时考虑运输成本、回收成本、物流信息的不确定性对供应链网络的影响；c）考虑制造中心中断情况时，配送中心及运输过程中面临的中断风险，研究多级设施中断对供应链网络的影响。

参考文献：

[1]Azizi V， Hu Guiping， Mokari M. A two-stage stochastic programming model for multi-period reverse logistics network design with lot-sizing［J］.Computers & Industrial Engineering，2020，143：106397.

［2]Goodarzian F， Wamba S F， Mathiyazhagan K， et al. A new bi-objective green medicine supply chain network design under fuzzy environment： hybrid metaheuristic algorithms［J］.Computers & Industrial Engineering，2021，160：107535.

［3]Yu Hai， Solvang W D. A fuzzy-stochastic multi-objective model for sustainable planning of a closed-loop supply chain considering mixed uncertainty and network flexibility［J］.Journal of Cleaner Production，2020，266：121702.

［4]Pudasaini P. Integrated planning of downstream petroleum supply chain：a multi-objective stochastic approach［J］.Operations Research Perspectives，2021，8：100189.

［5]You Fengqi， Wassick J M， Grossmann I E. Risk management for a global supply chain planning under uncertainty：models and algorithms［J］.AIChE Journal，2009，55（4）：931-946.

［6]Peidro D， Mula J， Poler R， et al. Fuzzy optimization for supply chain planning under supply， demand and process uncertainties［J］.Fuzzy Sets and Systems，2009，160（18）：2640-2657.

［7]Tolooie A， Maity M， Sinha A K. A two-stage stochastic mixed-integer program for reliable supply chain network design under uncertain disruptions and demand［J］.Computers & Industrial Engineering，2020，148：106722.

［8]Vali-Siar M M， Roghanian E. Sustainable， resilient and responsive mixed supply chain network design under hybrid uncertainty with considering COVID-19 pandemic disruption［J］.Sustainable Production and Consumption，2022，30：278-300.

［9]Yin Mingqiang， Huang Min， Wang Xingwei， et al. Fourth-party logistics network design under uncertainty environment［J］.Computers & Industrial Engineering，2022，167：108002.

［10]王振，郭健全.模糊環境下考虑供应中断的再制造闭环供应链研究［J］.工业工程，2021，24（1）：140-146.（Wang Zhen， Guo Jianquan. Research on remanufacturing closed-loop supply chain conside-ring supply disruption in fuzzy environment［J］.Industrial Enginee-ring，2021，24（1）：140-146.）

［11]狄卫民，王然.考虑多级设施中断的供应链选址—库存决策模型及优化算法［J］.计算机集成制造系统，2021，27（1）：270-283.（Di Weimin， Wang Ran. Supply chain location-inventory decision model and optimization algorithm considering multi-echelon facility disruption［J］.Computer Integrated Manufacturing Systems，2021，27（1）：270-283.）

［12]Bertsimas D， Sim M. The price of robustness［J］.Operations Research，2004，52（1）：35-53.

［13]于冬梅，高雷阜，赵世杰.不确定与损毁情景下可靠性设施选址鲁棒优化模型与算法研究［J］.系统工程理论与实践，2019，39（2）：498-508.（Yu Dongmei， Gao Leifu， Zhao Shijie. Research on robust optimization model and algorithm for reliability facility location under uncertainty and damage scenarios［J］.Systems Engineering-Theory & Practice，2019，39（2）：498-508.）

［14]Gholizadeh H， Fazlollahtabar H. Robust optimization and modified genetic algorithm for a closed loop green supply chain under uncertainty： case study in melting industry［J］.Computers & Industrial Engineering，2020，147：106653.

［15]Attia A M. A multi-objective robust optimization model for upstream hydrocarbon supply chain［J］.Alexandria Engineering Journal，2021，60（6）：5115-5127.

［16]邱若臻，肖欣，孙艺萌，等.不确定环境下的鲁棒多产品、多周期供应链网络设计模型［J］.计算机集成制造系统，2019，25（10）：2655-2665.（Qiu Ruozhen， Xiao Xin， Sun Yimeng， et al. Robust multi-product and multi-period supply chain network design model under uncertain environment［J］.Computer Integrated Manufacturing Systems，2019，25（10）：2655-2665.）

［17]董海，高秀秀，魏铭琦.基于动态自适应布谷鸟搜索算法的多目标闭环供应链网络优化［J］.系统工程，2020，38（4）：46-58.（Dong Hai， Gao Xiuxiu， Wei Mingqi. Multi-objective closed-loop supply chain network optimization based on dynamic adaptive cuckoo search algorithm［J］.System Engineering，2020，38（4）：46-58.）

［18]尉迟群丽，何正文，王能民.考虑缺货的闭环供应链选址—库存—路径集成优化［J］.运筹与管理，2021，30（2）：53-60.（Yuchi Qunli， He Zhengwen， Wang Nengmin. Integrated location-inventory-routing optimization of closed-loop supply chain considering shortage［J］.Operations Research and Management Science，2021，30（2）：53-60.）

［19]Abbassi A， Kharraja S， Alaoui A E H， et al. Multi-objective two-echelon location-distribution of non-medical products［J］.International Journal of Production Research，2021，59（17）：5284-5300.

［20]Liao Yi， Kaviyani-Charati M， Hajiaghaei-Keshteli M， et al. Designing a closed-loop supply chain network for citrus fruits crates conside-ring environmental and economic issues［J］.Journal of Manufactu-ring Systems，2020，55：199-220.

［21]Tirkolaee E B， Goli A， Ghasemi P， et al. Designing a sustainable closed-loop supply chain network of face masks during the COVID-19 pandemic：Pareto-based algorithms［J］.Journal of Cleaner Production，2022，333：130056.

［22]Li Kang， Li Dan， Wu Daqing. Carbon transaction-based location-routing-inventory optimization for cold chain logistics［J］.Alexandria Engineering Journal，2022，61（10）：7979-7986.

收稿日期：2023-02-16；修回日期：2023-04-20

基金項目：陕西省科技厅项目（2023YBGY408）；陕西省社会科学基金资助项目（2020R043）；西安市科技局项目（21RKYJ0023）;陕西省重点研发计划项目（2023-YBGY-408）；西安市科技计划项目（23RKYJ0026）

作者简介：孙军艳（1978-），女，陕西大荔人，副教授，硕导，博士，主要研究方向为物流信息、供应链管理；陈泽飞（1999-），男（通信作者），山西运城人，硕士研究生，主要研究方向为供应链管理（1173243421@qq.com）；陈智瑞（1997-），女，陕西汉中人，硕士，主要研究方向为供应链管理；李晓朋（1999-），男，河北邢台人，硕士研究生，主要研究方向为车间调度.